计算机学院 2017 春季七校联合 《离散数学》试卷 A 卷 闭卷 考试时间： 2016 年 5 月 13 日 班级__________学号____________________姓名________________ 题号 一 题分 15 得分 二 15 三 40 四 30 总分 核对人 100 得分 评卷人 一. 单项选择（每小题 2 分，总共 20 分） ( ) 1. 由甲、乙、丙、丁、戊 5 位学生中选一个班长和一个团支书， 若甲必须任职，有多少种选法？ （A）20 （B）16 （C）8 ) 2. 从 1 到 20 中至少任意选出多少个数，使得其中有两个数的和 （D）4 （A）12 （B）11 （C）10 （D）9 ) 3. 下列哪个是常系数二阶线性齐次递推关系？ （A） （B） 22  2 a  n  2 a n a n a n  （C） a n  2 a 1-n  a n  2 （D） a n  2 an n   1 a n  2 ( 是 21？ ( ( ) 4. 点数最少的非平面图是： （A）K4 （C）K3,3 ) 5. 设 G 是一个树林，由 5 个分图（连通分支）组成，若 G 有 15 （B）K5 （D）K2,3 ( 个结点，问 G 有多少条边？ （A）12 （B）11 （C）10 1 （D）9 

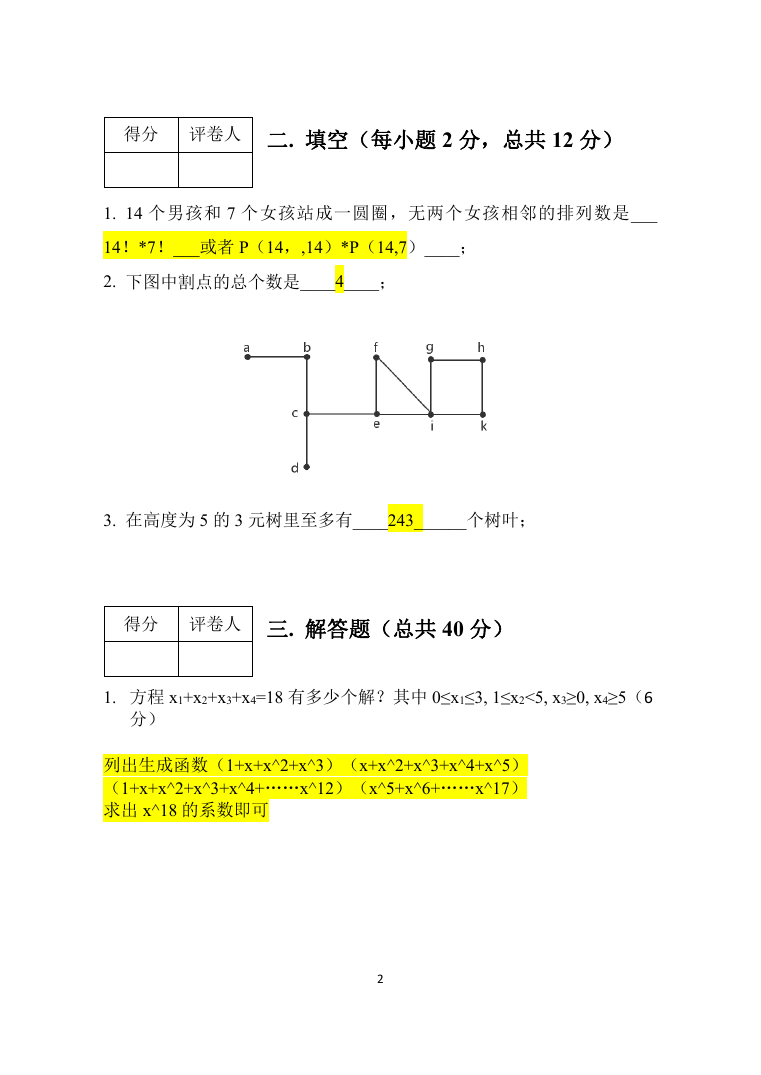
得分 评卷人 二. 填空（每小题 2 分，总共 12 分） 1. 14 个男孩和 7 个女孩站成一圆圈，无两个女孩相邻的排列数是___ 14！*7！___或者 P（14，,14）*P（14,7）____； 2. 下图中割点的总个数是____4____； 3. 在高度为 5 的 3 元树里至多有____243______个树叶； 得分 评卷人 三. 解答题（总共 40 分） 1. 方程 x1+x2+x3+x4=18 有多少个解？其中 0≤x1≤3, 1≤x2<5, x3≥0, x4≥5（6 分） 列出生成函数（1+x+x^2+x^3）（x+x^2+x^3+x^4+x^5） （1+x+x^2+x^3+x^4+……x^12）（x^5+x^6+……x^17） 求出 x^18 的系数即可 2 

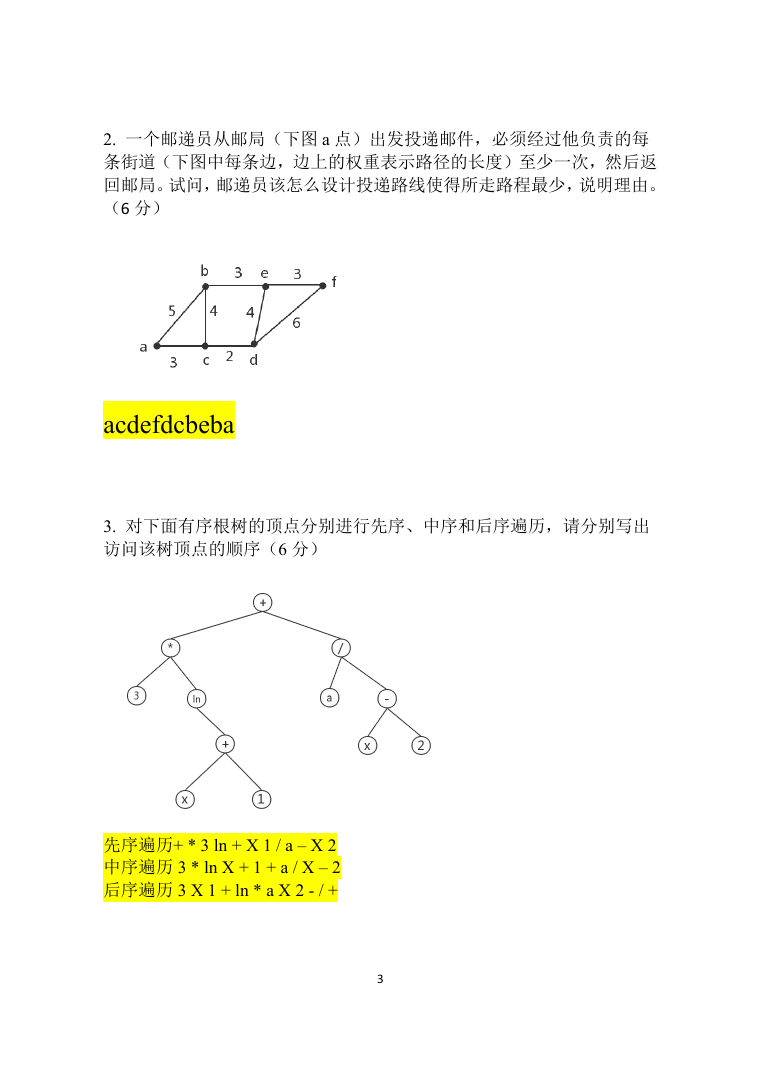
2. 一个邮递员从邮局（下图 a 点）出发投递邮件，必须经过他负责的每 条街道（下图中每条边，边上的权重表示路径的长度）至少一次，然后返 回邮局。试问，邮递员该怎么设计投递路线使得所走路程最少，说明理由。 （6 分） acdefdcbeba 3. 对下面有序根树的顶点分别进行先序、中序和后序遍历，请分别写出 访问该树顶点的顺序（6 分） 先序遍历+ * 3 ln + X 1 / a – X 2 中序遍历 3 * ln X + 1 + a / X – 2 后序遍历 3 X 1 + ln * a X 2 - / + 3 

得分 评卷人 四. 证明题（每小题 10 分，总共 30 分） 1. 证明 G 和G（G 的补图）有一个是连通图。 假设 G 不是连通图 G=(V,E)，则 G 的补图 G~=(V,E’)。 则 E’是完全图 Kn(假设 G 有 n 个顶点)的边减去图 G 的边所得。 若 G 有任意两个顶点 v1，v2。若 v1，v2 在同一个连通分支中则 v1 和 v2 连通，若 v1，v2 不在一个连通分支中，则其他一个连通分支中存在一个 点在补图 G~中 v3 与 v1，v3 与 v2 相连，所以说 v1 和 v2 就相连通。 因为 v1，v2 是任意的，所以 G 和 G 的补图中有一个是连通图。 2. 证明存在有五个顶点的三棵树两两不同构。 这题只要证明存在就行了，五个顶点，三棵树，画出三个不同构的树 就行 4