人工智能搜索策略上.doc

发布时间：2022-06-18 发布人：admin 分类：说明书资料大小：0.12M 资料格式：doc 举报版权申诉

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第1页.png

第1页 / 共7页

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第2页.png

第2页 / 共7页

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第3页.png

第3页 / 共7页

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第4页.png

第4页 / 共7页

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第5页.png

第5页 / 共7页

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第6页.png

第6页 / 共7页

24a19122-75c3-49bc-a6d2-9fd45800a740.doc.pdf-第7页.png

第7页 / 共7页

文本预览

人工智能搜素策略状态空间盲目搜索广度优先搜素(Breadth-First-Search) 深度优先搜素(Depth-First-Search) 代价树搜索状态空间启发搜索 A 星搜索算法(A Star search algorithm) 状态空间盲目搜索首先是思想基础，在此我罗列了 BFS 和 DFS 的科学定义，另还有我的通俗解释广度优先搜索：从初始节点 S0开始逐层向下扩展，在第 n 层节点还没有全部搜索完之前，不进入第 n+1层节点的搜索。Open 表中的节点总是按进入的先后排序，先进入的节点排在前面，后进入的节点排在后面。深度优先搜索：从初始节点 S0开始，在其子节点中选择一个最新生成的节点进行考察，如果该子节点不是目标节点且可以扩展，则扩展该子节点，然后再在此子节点的子节点中选择一个最新生成的节点进行考察，依此向下搜索，直到某个子节点既不是目标节点，又不能继续扩展时，才选择其兄弟节点进行考察。如果你对上述的定义感到讨厌 ( 当然这是不好的 ) ，不妨看看下面我的通俗解释：

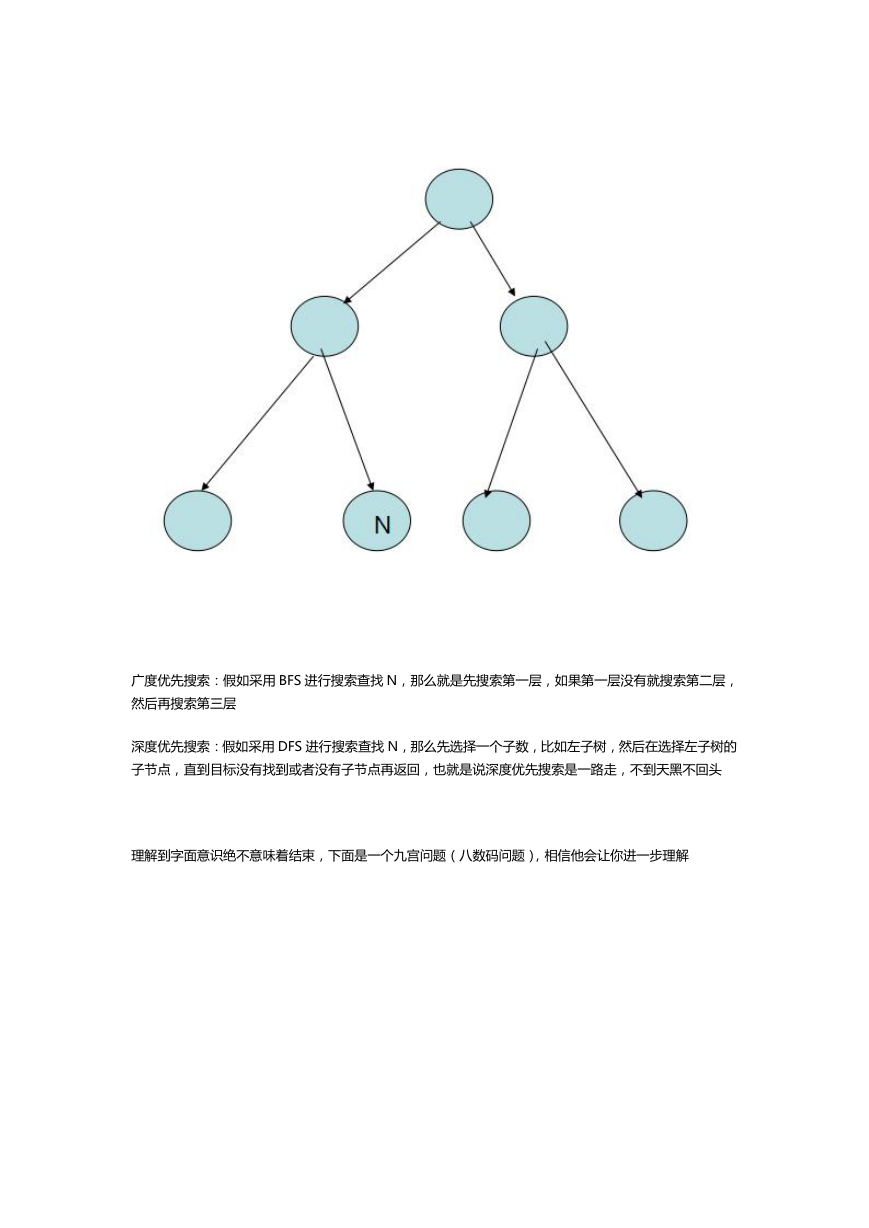
广度优先搜索：假如采用 BFS 进行搜索查找 N，那么就是先搜索第一层，如果第一层没有就搜索第二层，然后再搜索第三层深度优先搜索：假如采用 DFS 进行搜索查找 N，那么先选择一个子数，比如左子树，然后在选择左子树的子节点，直到目标没有找到或者没有子节点再返回，也就是说深度优先搜索是一路走，不到天黑不回头理解到字面意识绝不意味着结束，下面是一个九宫问题（八数码问题），相信他会让你进一步理解

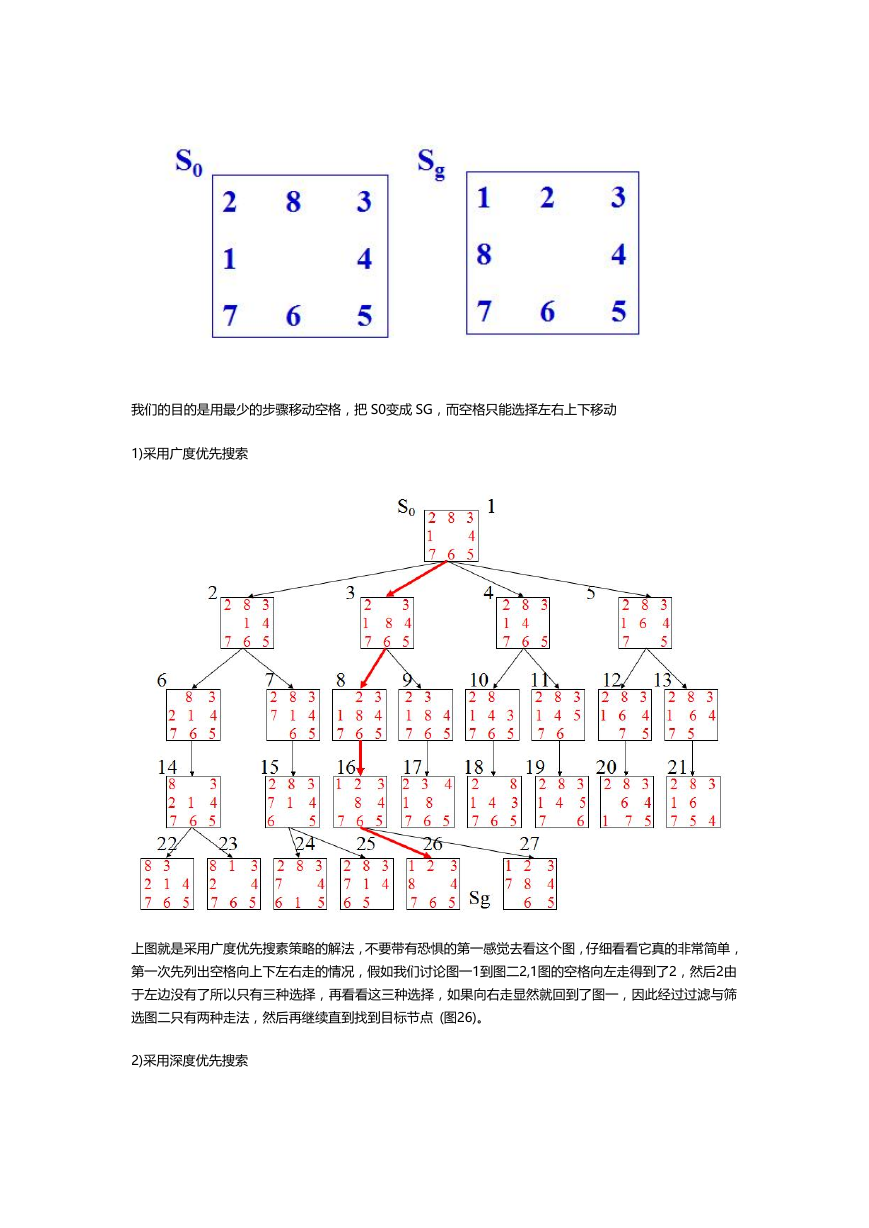
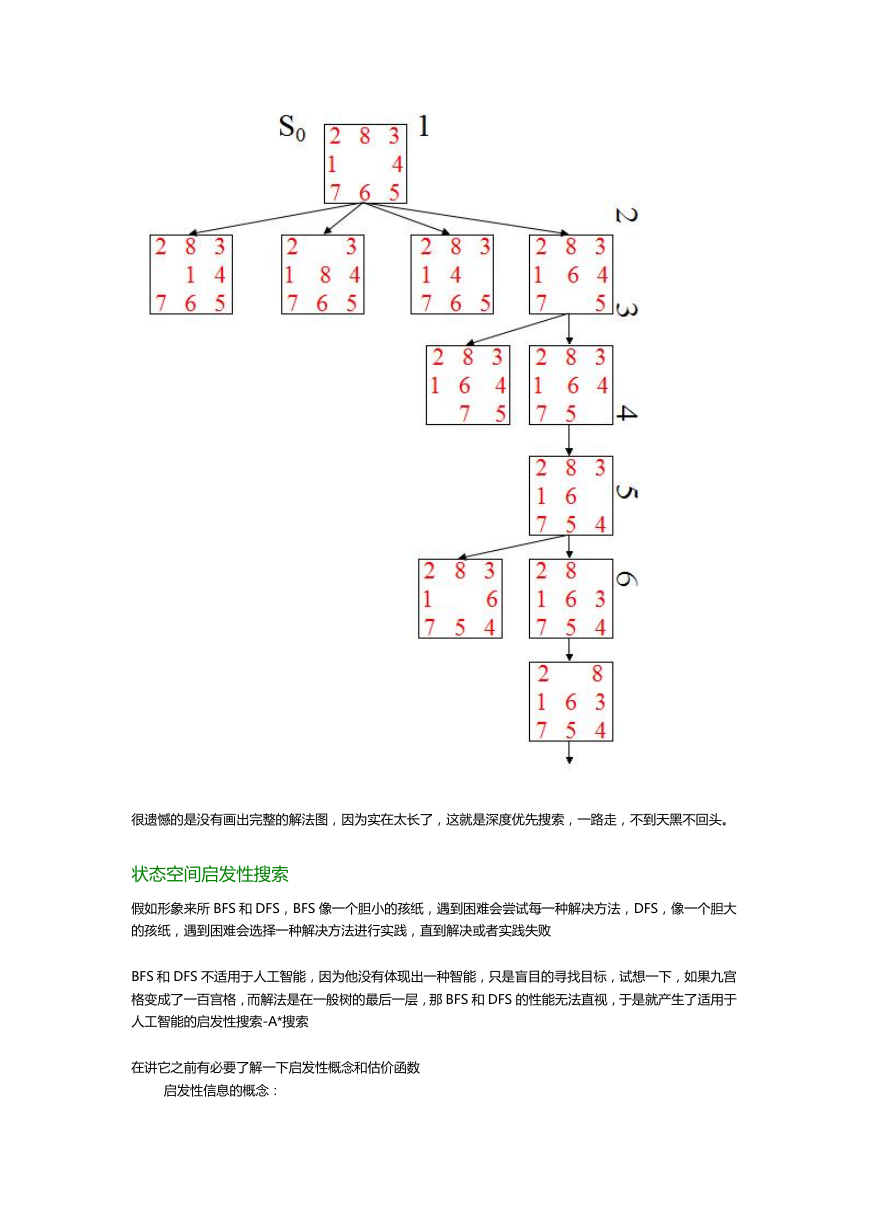
我们的目的是用最少的步骤移动空格，把 S0变成 SG，而空格只能选择左右上下移动 1)采用广度优先搜索上图就是采用广度优先搜素策略的解法，不要带有恐惧的第一感觉去看这个图，仔细看看它真的非常简单，第一次先列出空格向上下左右走的情况，假如我们讨论图一1到图二2,1图的空格向左走得到了2，然后2由于左边没有了所以只有三种选择，再看看这三种选择，如果向右走显然就回到了图一，因此经过过滤与筛选图二只有两种走法，然后再继续直到找到目标节点 (图26)。 2)采用深度优先搜索

很遗憾的是没有画出完整的解法图，因为实在太长了，这就是深度优先搜索，一路走，不到天黑不回头。状态空间启发性搜索假如形象来所 BFS 和 DFS，BFS 像一个胆小的孩纸，遇到困难会尝试每一种解决方法，DFS，像一个胆大的孩纸，遇到困难会选择一种解决方法进行实践，直到解决或者实践失败 BFS 和 DFS 不适用于人工智能，因为他没有体现出一种智能，只是盲目的寻找目标，试想一下，如果九宫格变成了一百宫格，而解法是在一般树的最后一层，那 BFS 和 DFS 的性能无法直视，于是就产生了适用于人工智能的启发性搜索-A*搜索在讲它之前有必要了解一下启发性概念和估价函数启发性信息的概念：

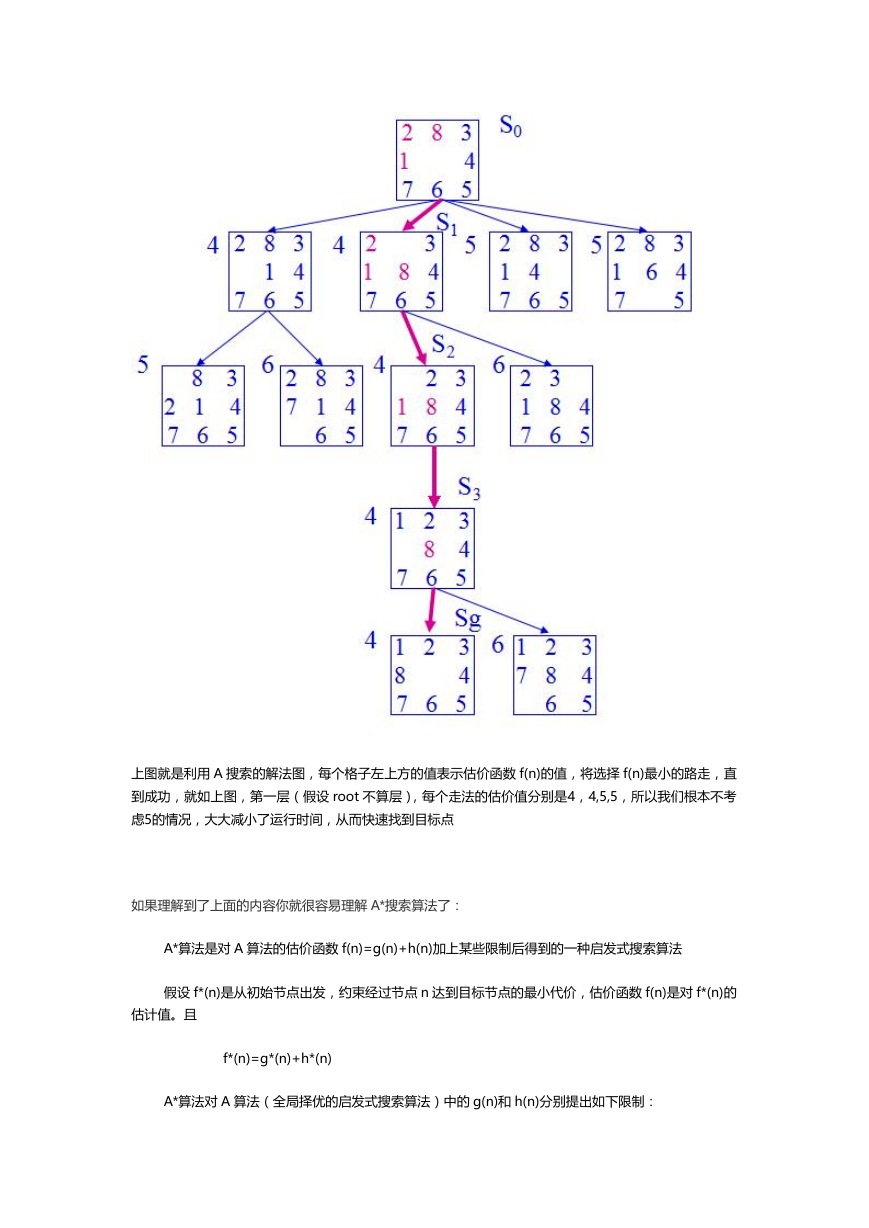
启发性信息是指那种与具体问题求解过程有关的，并可指导搜索过程朝着最有希望方向前进的控制信息。估价函数：用来估计节点重要性的函数。估价函数 f(n)被定义为从初始节点 S0 出发，约束经过节点 n 到达目标节点 Sg 的所有路径中最小路径代价的估计值。它的一般形式为： f(n)=g(n)+h(n) 其中，g(n)是从初始节点 S0 到节点 n 的实际代价；h(n)是从节点 n 到目标节点 Sg 的最优路径的估计代价。如果时间充足建议你多度一下上方绿色部分，并记住上面的形式，它将会很有用还是接着上面的九宫问题，如果我们考虑用 A*搜解决就可以设估价函数如下： f(n)=d(n)+W(n) d(n)表示节点 n 在一般搜索树中的深度 W(n)表示节点与 Sg 不匹配的个数，W(n)的值越大就表明这个方法离成功越远

上图就是利用 A 搜索的解法图，每个格子左上方的值表示估价函数 f(n)的值，将选择 f(n)最小的路走，直到成功，就如上图，第一层（假设 root 不算层），每个走法的估价值分别是4，4,5,5，所以我们根本不考虑5的情况，大大减小了运行时间，从而快速找到目标点如果理解到了上面的内容你就很容易理解 A*搜索算法了： A*算法是对 A 算法的估价函数 f(n)=g(n)+h(n)加上某些限制后得到的一种启发式搜索算法假设 f*(n)是从初始节点出发，约束经过节点 n 达到目标节点的最小代价，估价函数 f(n)是对 f*(n)的估计值。且 f*(n)=g*(n)+h*(n) A*算法对 A 算法（全局择优的启发式搜索算法）中的 g(n)和 h(n)分别提出如下限制：

第一，g(n)是对最小代价 g*(n)的估计，且 g(n)>0；第二，h(n)是最小代价 h*(n)的下界，即对任意节点 n 均有 h(n)≤h*(n)。即满足上述两条限制的 A 算法称为 A*算法。

分享到：

赞收藏

资料库

人工智能搜索策略上.doc

相关推荐

信息化

热门标签

最新资料