logo资料库

模糊控制在一级倒立摆中的应用及 MATLAB 仿真.doc

发布时间：2022-06-02 发布人：admin 分类：说明书 资料大小：0.83M 资料格式：doc 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    先进控制技术（贾润达、王姝） 结课报告 模糊控制在一级倒立摆中的应用及 MATLAB 仿真 课程名称： 先 进 控 制 技 术 姓 学 名： 号： 刘 畅 1301141 专业班级： 信 息 三 班
    一、模糊控制方法概述 模糊控制方法是以模糊数学为基础,用语言规则表示方法和先进的计算机技 术,由模糊推理进行决策的一种高级控制策。模糊控制作为以模糊集合论、模糊语 言变量及模糊逻辑推理为基础的一种计算机数字控制，它已成为目前实现智能控 制的一种重要而又有效的形式尤其是模糊控制和神经网络、遗传算法及混沌理论 等新学科的融合，正在显示出其巨大的应用潜力。实质上模糊控制是一种非线性 控制，从属于智能控制的范畴。 模糊控制的突出特点在于： 1）控制系统的设计不要求知道被控对象的精确数学模型，只需要提供现场操作人 员的经验知识及操作数据。 2）控制系统的鲁棒性强，适用于解决常规控制难以解决的非线性、时变及大滞后 等问题。 3）以语言变量代替常规的数学变量，易于形成专家的“知识”。 4）控制系统采用“不精确推理”。推理过程模仿人的思维过程。由于介入了人的 经验，因而能够处理复杂甚至“病态”系统。 二、一级倒立摆的模糊数学模型 首先采用牛顿一欧拉方法建立直线型一级倒立摆系统的数学模型。主要是针 对倒立摆系统中小车和摆杆的受力分析及其微分方程，现给出如下：  2 dml 2  2 dt   m  lg sin      tu （1） 这里m是摆杆的质量，l是摆长，是从垂直方向上的顺时针偏转角，=u（t）为 作用于杆的逆时针扭矩（u（t）是控制作用）,t是时间，g是重力加速度常数。 假设 x 1    x 2 , d  dt 为状态变量，有等式（1）给出的非线性系统的的状态 空间表达式为 xd 1 dt  x 2 xd 2 dt   lg  sin  x 1    1    tuml 2    xlg 1   1 若所测 1x 用度表示， 2x 用每秒度表示，当取l=g和m= 180 间状态空间表达式可用矩阵差分方程表式  kx 1  1    kx 1   kx 2  kx 2  1    kx 1    kx 2   ku 2 （足够小）   tuml  g 时，线性离散时 2 然后进行模糊化设计（利用Mamdani模糊模型），在此问题中，设上述两变
    量的论域为   2  x 1   2 和  5 rad s  x 2  5 rad s ,则设计步骤为： 第1步。首先，对 1x 在其论域上建立三个隶属度函数，即正值（P）、零（Z）和负 值（N）。然后，对 2x 在其论域上亦建立3个隶属度函数，同样是正值（P）、零（Z） 和负值（N）。 第2步。为划分控制空间（输出），对  ku 在其论域上建立5个隶属度函数，  24    24 ku  。 第3步。用表1所示的3*3规则表的格式建立9条规则（即使我们可能不需要这么多）。 d 。表中的输出即为控制作用u(t)。 本系统中为使倒立摆系统稳定，将用到和 dt X1 X2 P Z N P PB P Z Z P Z N N Z N NB 第 4 步。我们可用表 1 中规则导出该控制问题的模型。并用图解法来推导模糊 表 1 模糊控制规则表 运算。假设初始条件为   01 x  1 和   02 x  4 rad s 0 3 然后，我们在上例中取离散步长  k ，并用矩阵差分方程式导出模型的四 步循环式。模型的每步循环式都会引出两个输入变量的隶属度函数，规则表产生 控制作用 u(k)的隶属度函数。我们将用重心法对控制作用的隶属度函数进行精确 化，用递归差分方程解得新的 1x 和 2x 值为开始，并作为下一步递归差分方程式的 输入条件。 分别为 1x 和 2x 的初始条件。从模糊规则表（表 1）有： If( 1x =P)and( 2x =Z),then(u=P) If( 1x =P)and( 2x =N),then(u=Z) If( 1x =Z)and( 2x =Z),then(u=Z) If( 1x =Z)and( 2x =N),then(u=N) 表示了控制变量 u 的截尾模糊结果的并。利用重心法精确化计算后的控制值
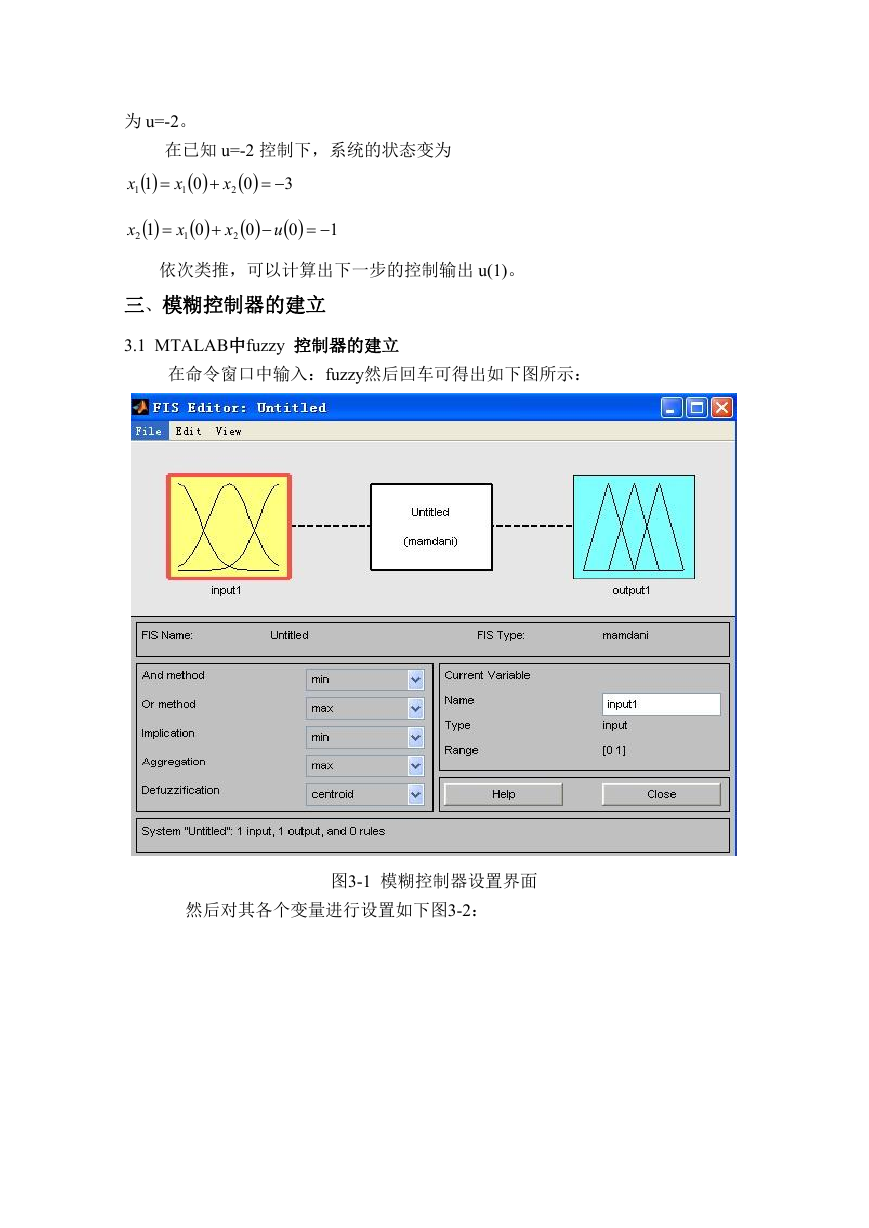
    为 u=-2。 在已知 u=-2 控制下，系统的状态变为 x  1   0   0  3  x 2   1 x 1   1  x 2   0  x 1 x 2   0    0 u  1 依次类推，可以计算出下一步的控制输出 u(1)。 三、模糊控制器的建立 3.1 MTALAB中fuzzy 控制器的建立 在命令窗口中输入：fuzzy然后回车可得出如下图所示： 图3-1 模糊控制器设置界面 然后对其各个变量进行设置如下图3-2：
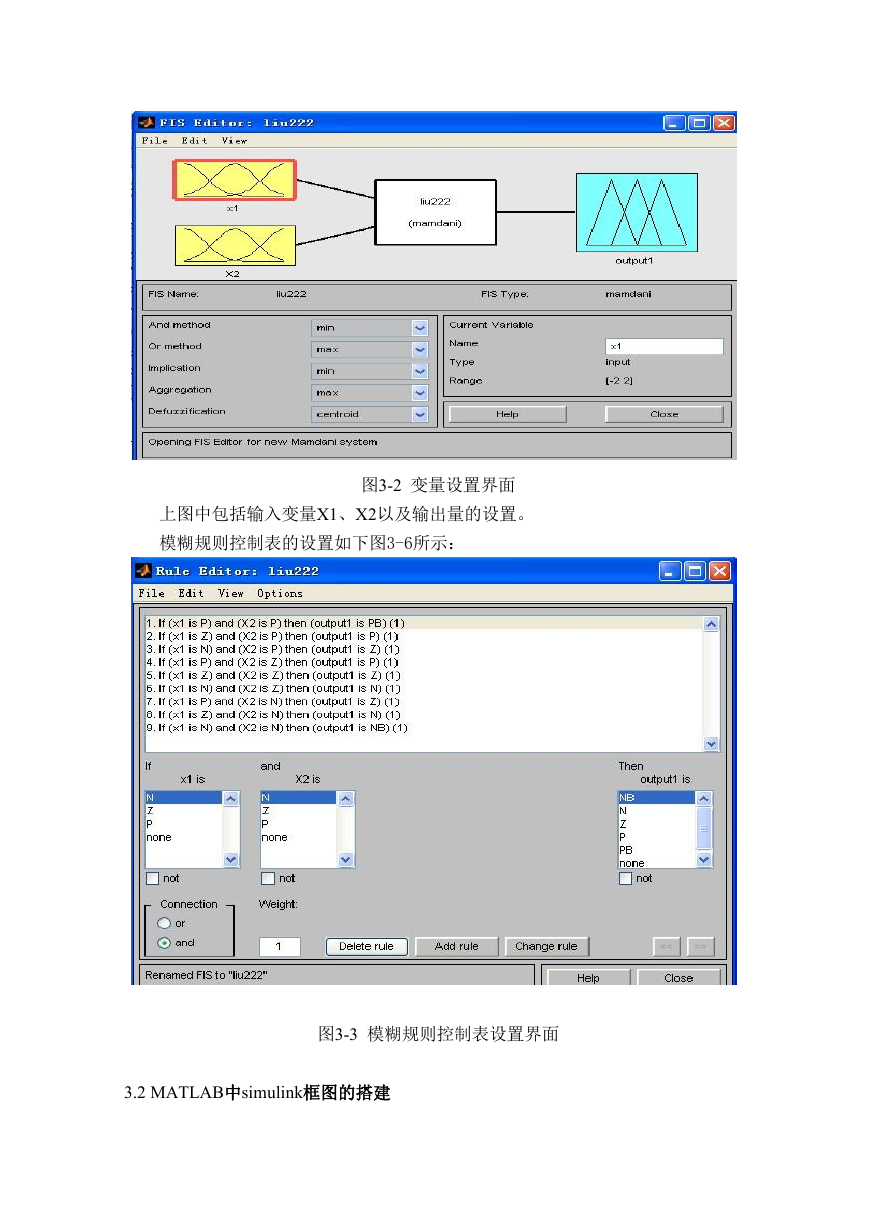
    图3-2 变量设置界面 上图中包括输入变量X1、X2以及输出量的设置。 模糊规则控制表的设置如下图3-6所示： 图3-3 模糊规则控制表设置界面 3.2 MATLAB中simulink框图的搭建
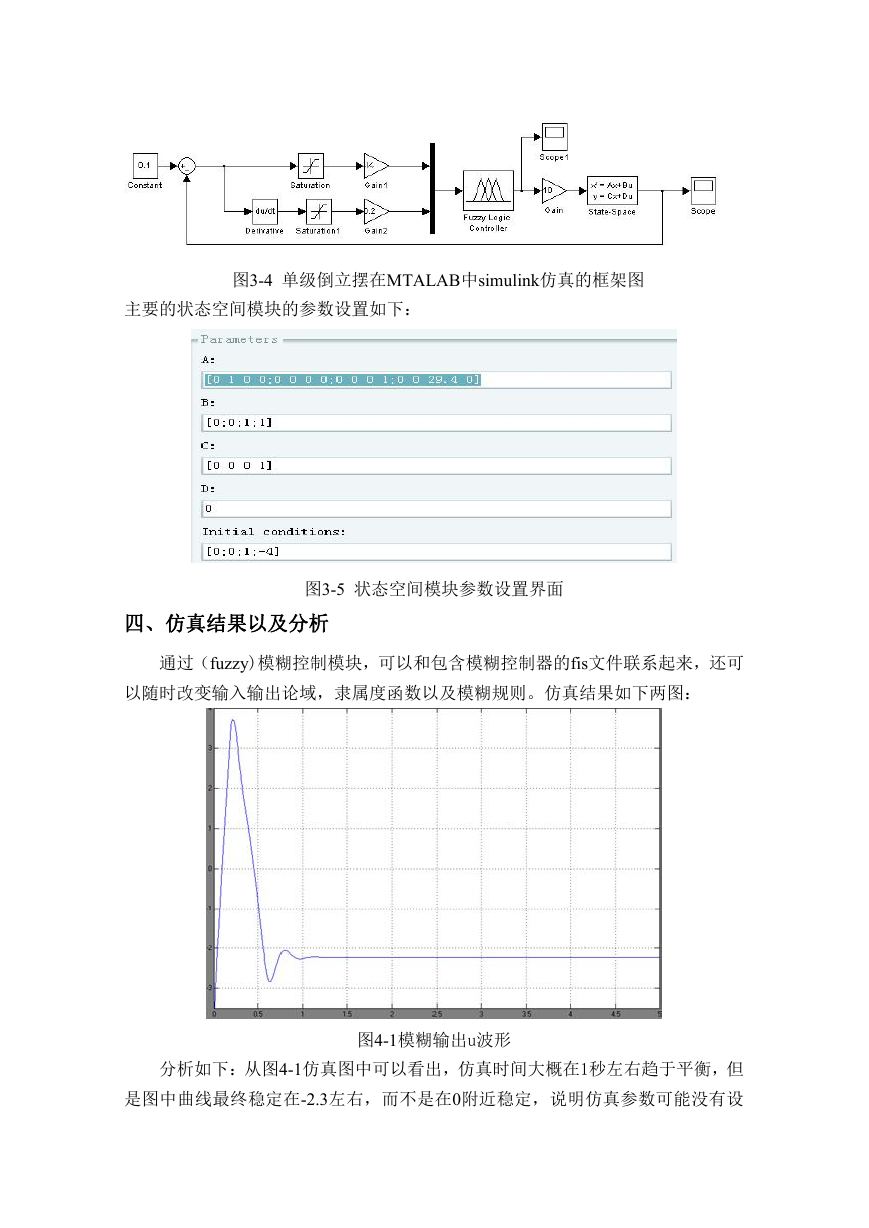
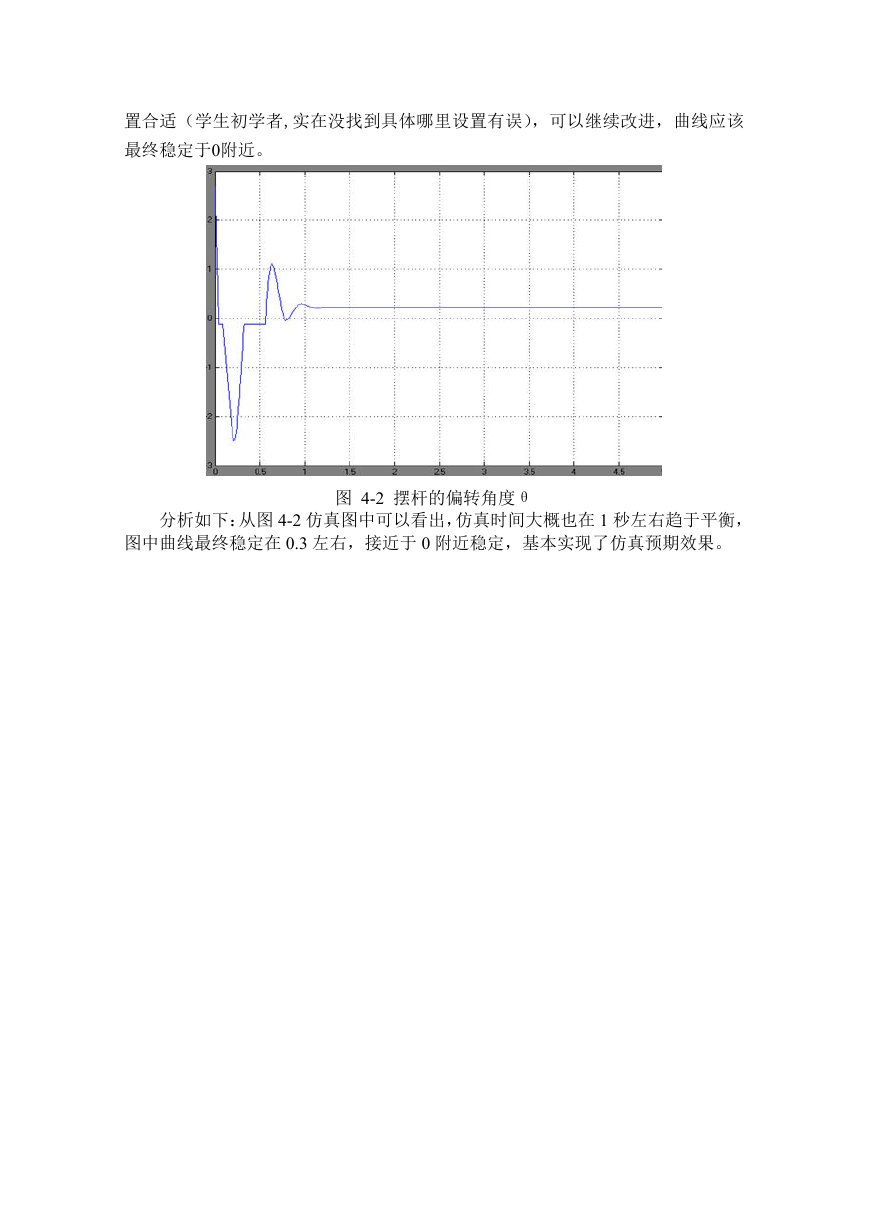
    图3-4 单级倒立摆在MTALAB中simulink仿真的框架图 主要的状态空间模块的参数设置如下： 图3-5 状态空间模块参数设置界面 四、仿真结果以及分析 通过（fuzzy)模糊控制模块，可以和包含模糊控制器的fis文件联系起来，还可 以随时改变输入输出论域，隶属度函数以及模糊规则。仿真结果如下两图： 图4-1模糊输出u波形 分析如下：从图4-1仿真图中可以看出，仿真时间大概在1秒左右趋于平衡，但 是图中曲线最终稳定在-2.3左右，而不是在0附近稳定，说明仿真参数可能没有设
    置合适（学生初学者,实在没找到具体哪里设置有误），可以继续改进，曲线应该 最终稳定于0附近。 分析如下：从图 4-2 仿真图中可以看出，仿真时间大概也在 1 秒左右趋于平衡， 图中曲线最终稳定在 0.3 左右，接近于 0 附近稳定，基本实现了仿真预期效果。 图 4-2 摆杆的偏转角度θ
    智能故障诊断方法简介 —基于人工神经网络的智能诊断方法 当今工业和国防的发展迅速，故障诊断技术已成为一个十分活跃的研究领域。 现有的故障诊断方法，概括起来可分为三大类（1）基于信号处理的方法（2）基 于解析模型的方法（3）基于知识的诊断方法。其中的解析模型方法已经得到了深 入的研究；但在实际情况中，常常难以获得对象的精确数学模型，这就大大限制 了其使用范围和效果。于是在 20 世纪 80 年代，人工智能及计算机技术的飞速发 展，为故障诊断技术提供了新的理论基础以后，产生了基于知识的故障诊断方法， 此方法由于不需要对象的精确数学模型，而且具有某些“智能”特性，因此是一 种很有生命力的方法。国内外专家学者陆续开发了一大批基于知识的故障诊断系 统，基于神经网络的智能诊断方法就是其中非常常用的一种。 神经网络故障诊断方法就是基于人工神经网络技术建立起来的。人工神经网 络由于其本身信息处理特点，如并行性、自学习、自组织性、联想记忆等功能， 使其能够解决那些传统模式识别方法难以圆满解决的问题。人工神经网络以分布 的方式存储信息，利用网络的拓扑结构和权值分布实现非线性映射，并利用全局 并行处理实现从输入空间到输出空间的非线性信息变换。通过大量样本的训练， 调整各层神经元之间的连接权值，样本的信息就存储在这些权值当中。进行诊断 时，被诊断对象的信息通过输入层，经输入层、隐含层（可以是多层）、输出层神 经元之间的变化得出诊断结果。 基于人工神经网络的神经元结构，人们建立了多种人工神经网络结构模型如： BP 网络、ART 网络、Hopfield 网络、Boltzmann 机、BAM 网络和 SOM 网络等。 而 BAM 网络最适合多故障诊断场合。BAM 又称为双向联想存储器，其拓扑结构 如下图所示： 图 1 RAM 网络拓扑结构 构成 BAM 网络的是非线性神经元，为了能够适用于故障诊断，在建立的模型 中，输入和输出均采用二元值{0 ,1}表示。权值矩阵为： W   n 1i  T i YX i 式中， iX 为输入向量，也就是故障征兆； iY 为输出向量,即故障原因。 在BAM网络中，所有的突触信息均包含在一个 pn  的矩阵W 中，这个矩阵实 际上就是一个权值矩阵,当权值矩阵建立完成后,就能进行故障诊断了。 基于神经网络的故障诊断适用于具有复杂大系统的故障诊断场合，其已在化 工、电气、电子、机械、机器人、航空等多个领域得到了发展。此方法优点是具 有一定的联想能力和抗干扰能力，同时具有自学习能力。缺点是需要大量的训练 样 本 ， 解 释 能 力 差 ， 对 于 复 杂 系 统 的 计 算 量 过 大 。
    分享到：
    赞 收藏

    相关推荐

    资料库

    行业

    共收录7266份资料，累计15个分类，关注成员有19位，主要包括：物流,旅游,餐饮零售,网络游戏,咨询,金融,电子政务,外包,教育,制造,医疗,嵌入式,互联网,交通,电信

    热门标签

    物流 旅游 餐饮零售 网络游戏 咨询 金融 电子政务 外包 教育 制造 医疗 嵌入式 互联网 交通 电信

    最新资料