2019年重庆市中考数学试卷及答案.doc-资料库

第1页 / 共16页

第2页 / 共16页

第3页 / 共16页

第4页 / 共16页

第5页 / 共16页

第6页 / 共16页

第7页 / 共16页

第8页 / 共16页

2019 年重庆市中考数学试卷及答案一、选择题：（本大题 12 个小题，每小题 4 分，共 48 分） 1．下列各数中，比﹣1 小的数是（） A．2 B．1 C．0 D．﹣2 2．如图是由 4 个相同的小正方体组成的一个立体图形，其主视图是（） A． B． C． D． 3．如图，△ABO∽△CDO，若 BO＝6，DO＝3，CD＝2，则 AB的长是（） A．2 B．3 C．4 D．5 4．如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点 D，连结 OD．若 ∠C＝50°，则∠AOD的度数为（） A．40° B．50° C．80° D．100° 5．下列命题正确的是（） A．有一个角是直角的平行四边形是矩形 B．四条边相等的四边形是矩形 C．有一组邻边相等的平行四边形是矩形 D．对角线相等的四边形是矩形 6．估计（2 +6 ）× 的值应在（） A．4 和 5 之间 B．5 和 6 之间 C．6 和 7 之间 D．7 和 8 之间 7．《九章算术》中有这样一个题：今有甲乙二人持钱不知其数．甲得乙半而钱五十，乙得甲太半而钱亦五十．问甲、乙持钱各几何？其意思为：今有甲乙二人，不如其钱包里有多少钱，若乙把其一半的钱给甲，则甲的数为 50；而甲把其的钱给乙，则乙的钱数也为

50，问甲、乙各有多少钱？设甲的钱数为 x，乙的钱数为 y，则可建立方程组为（） A． B． C． D． 8．按如图所示的运算程序，能使输出 y值为 1 的是（） A．m＝1，n＝1 B．m＝1，n＝0 C．m＝1，n＝2 D．m＝2，n＝1 9．如图，在平面直角坐标系中，矩形 ABCD的顶点 A，D分别在 x轴、y轴上，对角线 BD∥x 轴，反比例函数 y＝（k＞0，x＞0）的图象经过矩形对角线的交点 E．若点 A（2，0）， D（0，4），则 k的值为（） A．16 B．20 C．32 D．40 10．为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比）i＝1：2.4 的山坡 AB上发现有一棵古树 CD．测得古树底端 C 到山脚点 A的距离 AC＝26 米，在距山脚点 A水平距离 6 米的点 E处，测得古树顶端 D的仰角∠AED＝48°（古树 CD与山坡 AB的剖面、点 E在同一平面上，古树 CD与直线 AE垂直），则古树 CD的高度约为（）（参考数据：sin48°≈0.73，cos48°≈0.67，tan48°≈1.11）

A．17.0 米 B．21.9 米 C．23.3 米 D．33.3 米 11．若关于 x的一元一次不等式组的解集是 x≤a，且关于 y的分式方程 ﹣ ＝1 有非负整数解，则符合条件的所有整数 a的和为（） A．0 B．1 C．4 D．6 12．如图，在△ABC中，D是 AC边上的中点，连结 BD，把△BDC沿 BD翻折，得到△BDC'， DC′与 AB交于点 E，连结 AC'，若 AD＝AC′＝2，BD＝3，则点 D到 BC′的距离为（） A． B． C． D．二、填空题：（本大题 6 个小题，每小题 4 分，共 24 分） 13．计算：（π﹣3）0+（）﹣1＝． 14．今年五一节期间，重庆市旅游持续火爆，全市共接待境内外游客超过 25600000 人次，请把数 25600000 用科学记数法表示为． 15．一个不透明的布袋内装有除颜色外，其余完全相同的 3 个红球，2 个白球，1 个黄球，搅匀后，从中随机摸出一个球，记下颜色后放回搅匀，再从中随机摸出一个球，则两次都摸到红球的概率为． 16．如图，在菱形 ABCD中，对角线 AC，BD交于点 O，∠ABC＝60°，AB＝2，分别以点 A、点 C为圆心，以 AO的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．（结果保留π） 17．某公司快递员甲匀速骑车前往某小区送物件，出发几分钟后，快递员乙发现甲的手机落在公司，无法联系，于是乙匀速骑车去追赶甲．乙刚出发 2 分钟时，甲也发现自己手机落在公司，立刻按原路原速骑车回公司，2 分钟后甲遇到乙，乙把手机给甲后立即原路原

速返回公司，甲继续原路原速赶往某小区送物件，甲乙两人相距的路程 y（米）与甲出发的时间 x（分钟）之间的关系如图所示（乙给甲手机的时间忽略不计）．则乙回到公司时，甲距公司的路程是米． 18．在精准扶贫的过程中，某驻村服务队结合当地高山地形，决定在该村种植中药材川香、贝母、黄连增加经济收入．经过一段时间，该村已种植的川香、贝母、黄连面积之比 4： 3：5，是根据中药材市场对川香、贝母、黄连的需求量，将在该村余下土地上继续种植这三种中药材，经测算需将余下土地面积的种植黄连，则黄连种植总面积将达到这三种中药材种植总面积的．为使川香种植总面积与贝母种植总面积之比达到 3：4，则该村还需种植贝母的面积与该村种植这三种中药材的总面积之比是．三、解答题：（本大题 7 个小题，每小题 10 分，共 70 分） 19．（10 分）计算：（1）（x+y）2﹣y（2x+y）（2）（a+ ）÷ 20．（10 分）如图，在△ABC中，AB＝AC，D是 BC边上的中点，连结 AD，BE平分∠ABC交 AC于点 E，过点 E作 EF∥BC交 AB于点 F．（1）若∠C＝36°，求∠BAD的度数；（2）求证：FB＝FE． 21．（10 分）每年夏季全国各地总有未成年人因溺水而丧失生命，令人痛心秩首．今年某校为确保学生安全，开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛．现从该校七、

八年级中各随机抽取 10 名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩得分用 x表示，共分成四组：A．80≤x＜85，B．85≤x＜90，C．90≤x＜95，D．95≤x≤100），下面给出了部分信息：七年级 10 名学生的竞赛成绩是：99，80，99，86，99，96，90，100，89，82 八年级 10 名学生的竞赛成绩在 C组中的数据是：94，90，94 七、八年级抽取的学生竞赛成绩统计表年级七年级八年级平均数中位数众数方差 92 93 c 52 92 b 100 50.4 根据以上信息，解答下列问题：（1）直接写出上述图表中 a，b，c的值；（2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握防溺水安全知识较好？请说明理由（一条理由即可）；（3）该校七、八年级共 730 人参加了此次竞赛活动，估计参加此次竞赛活动成绩优秀（x ≥90）的学生人数是多少？ 22．（10 分）《道德经》中的“道生一，一生二，二生三，三生万物”道出了自然数的特征．在数的学习过程中，我们会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等．现在我们来研究另一种特珠的自然数﹣“纯数”．定义；对于自然数 n，在计算 n+（n+1）+（n+2）时，各数位都不产生进位，则称这个自然数 n为“纯数”，例如：32 是”纯数”，因为计算 32+33+34 时，各数位都不产生进位；

23 不是“纯数”，因为计算 23+24+25 时，个位产生了进位．（1）判断 2019 和 2020 是否是“纯数”？请说明理由；（2）求出不大于 100 的“纯数”的个数． 23．（10 分）在初中阶段的函数学习中，我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质一一运用函数解决问题“的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时，我们也学习了绝对值的意义|a|＝．结合上面经历的学习过程，现在来解决下面的问题在函数 y＝|kx﹣3|+b中，当 x＝2 时， y＝﹣4；当 x＝0 时，y＝﹣1．（1）求这个函数的表达式；（2）在给出的平面直角坐标系中，请用你喜欢的方法面出这个函数的图象井写出这个函数的一条性质；（3）已知函 y＝ x﹣3 的图象如图所示，结合你所画的函数图象，直接写出不等式|kx ﹣3|+b≤ x﹣3 的解集． 24．（10 分）某文明小区 50 平方米和 80 平方米两种户型的住宅，50 平方米住宅套数是 80 平方米住宅套数的 2 倍．物管公司月底按每平方米 2 元收取当月物管费，该小区全部住宅都人住且每户均按时全额缴纳物管费．（1）该小区每月可收取物管费 90000 元，问该小区共有多少套 80 平方米的住宅？（2）为建设“资源节约型社会”，该小区物管公司 5 月初推出活动一：“垃圾分类送礼物”， 50 平方米和 80 平方米的住户分别有 40%和 20%参加了此次括动．为提离大家的积扱性，6 月份准备把活动一升级为活动二：“拉圾分类抵扣物管费”，同时终止活动一．经调査与测算，参加活动一的住户会全部参加活动二，参加活动二的住户会大幅增加，这样，6

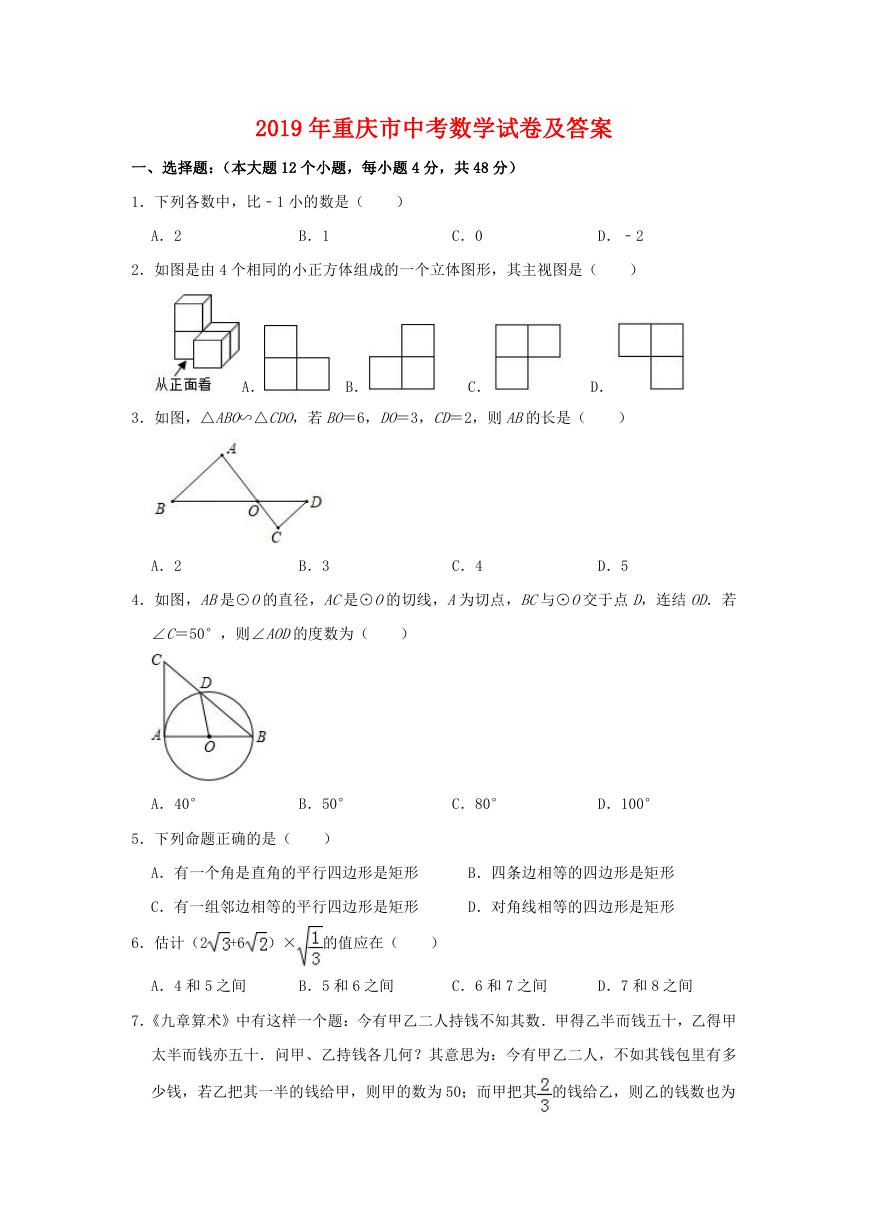
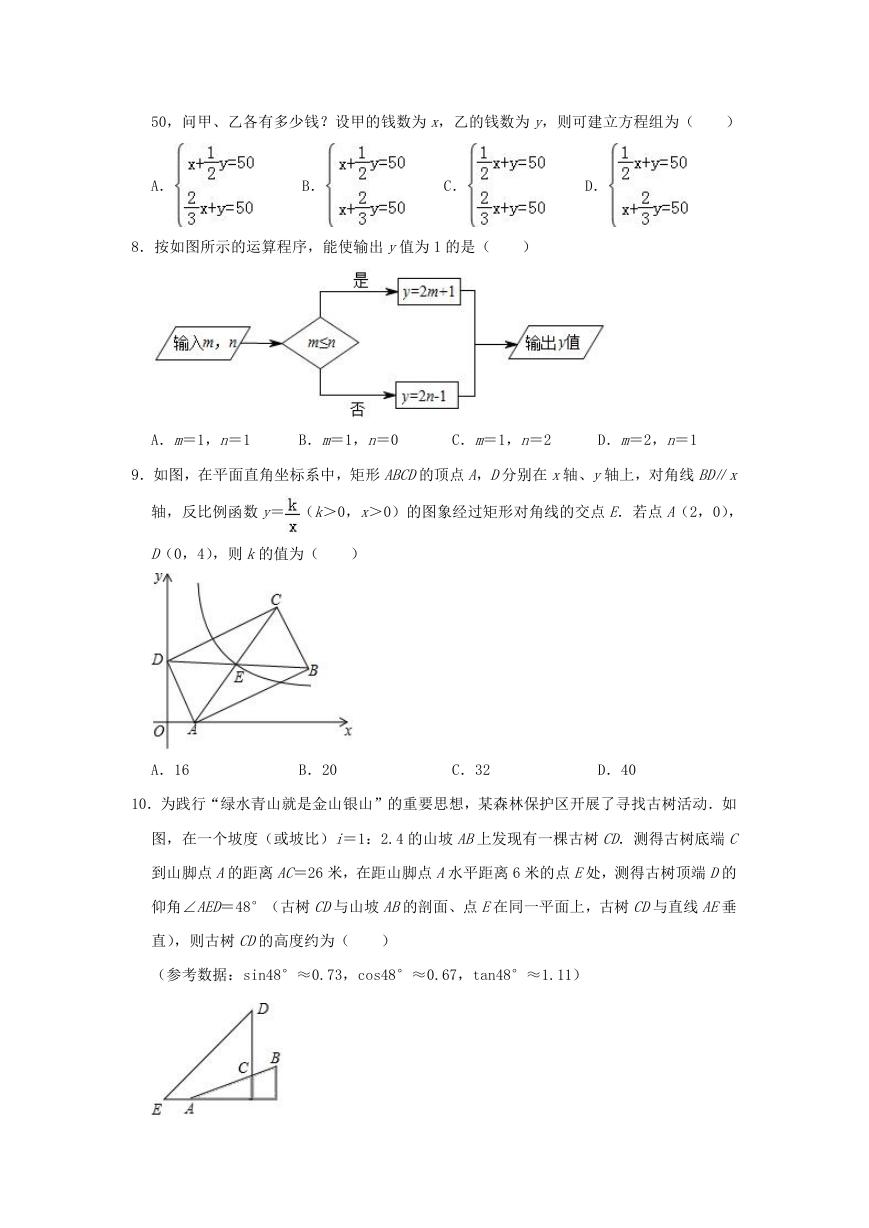
月份参加活动的 50 平方米的总户数在 5 月份参加活动的同户型户数的基础上将增加 2a%，每户物管费将会减少 a%；6 月份参加活动的 80 平方米的总户数在 5 月份参加活动的同户型户数的基础上将增加 6a%，每户物管费将会减少 a%．这样，参加活动的这部分住户 6 月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少 a%，求 a的值． 25．（10 分）如图，在平行四边形 ABCD中，点 E在边 BC上，连结 AE，EM⊥AE，垂足为 E，交 CD于点 M，AF⊥BC，垂足为 F，BH⊥AE，垂足为 H，交 AF于点 N，点 P是 AD上一点，连接 CP．（1）若 DP＝2AP＝4，CP＝，CD＝5，求△ACD的面积．（2）若 AE＝BN，AN＝CE，求证：AD＝ CM+2CE．四、解答题：（本大题 1 个小题，共 8 分） 26．（8 分）如图，在平面直角坐标系中，抛物线 y＝x2﹣2x﹣3 与 x轴交于点 A，B（点 A在点 B的左侧），交 y轴于点 C，点 D为抛物线的顶点，对称轴与 x轴交于点 E．（1）连结 BD，点 M是线段 BD上一动点（点 M不与端点 B，D重合），过点 M作 MN⊥BD，交抛物线于点 N（点 N在对称轴的右侧），过点 N作 NH⊥x轴，垂足为 H，交 BD于点 F，点 P是线段 OC上一动点，当 MN取得最大值时，求 HF+FP+ PC的最小值；（2）在（1）中，当 MN取得最大值，HF+FP+ PC取得最小值时，把点 P向上平移个单位得到点 Q，连结 AQ，把△AOQ绕点 O顺时针旋转一定的角度α（0°＜α＜360°），得到△A′OQ′，其中边 A′Q′交坐标轴于点 G．在旋转过程中，是否存在一点 G，使得 ∠Q'＝∠Q'OG？若存在，请直接写出所有满足条件的点 Q′的坐标；若不存在，请说明理由．

资料库

2019年重庆市中考数学试卷及答案.doc

相关推荐

中考

热门标签

最新资料