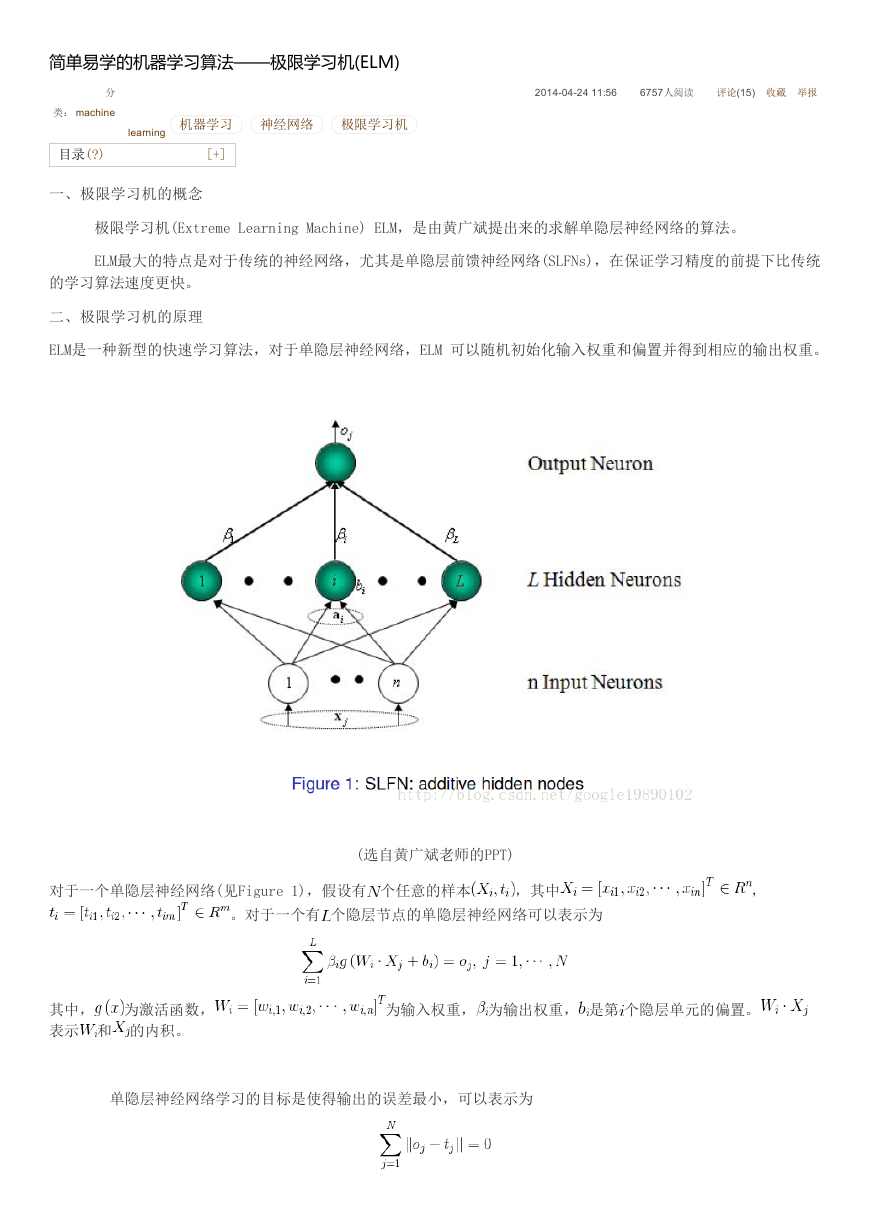
简单易学的机器学习算法——极限学习机(ELM) 分 类： machine learning 机器学习 神经网络 极限学习机 目录(?) [+] 一、极限学习机的概念 2014­04­24 11:56   6757人阅读   评论(15)   收藏   举报     极限学习机(Extreme Learning Machine) ELM，是由黄广斌提出来的求解单隐层神经网络的算法。     ELM最大的特点是对于传统的神经网络，尤其是单隐层前馈神经网络(SLFNs)，在保证学习精度的前提下比传统 的学习算法速度更快。 二、极限学习机的原理 ELM是一种新型的快速学习算法，对于单隐层神经网络，ELM 可以随机初始化输入权重和偏置并得到相应的输出权重。 对于一个单隐层神经网络(见Figure 1)，假设有 个任意的样本 ，其中 ， 。对于一个有 个隐层节点的单隐层神经网络可以表示为 (选自黄广斌老师的PPT) 其中， 为激活函数， 表示 和 的内积。 为输入权重， 为输出权重， 是第 个隐层单元的偏置。      单隐层神经网络学习的目标是使得输出的误差最小，可以表示为 

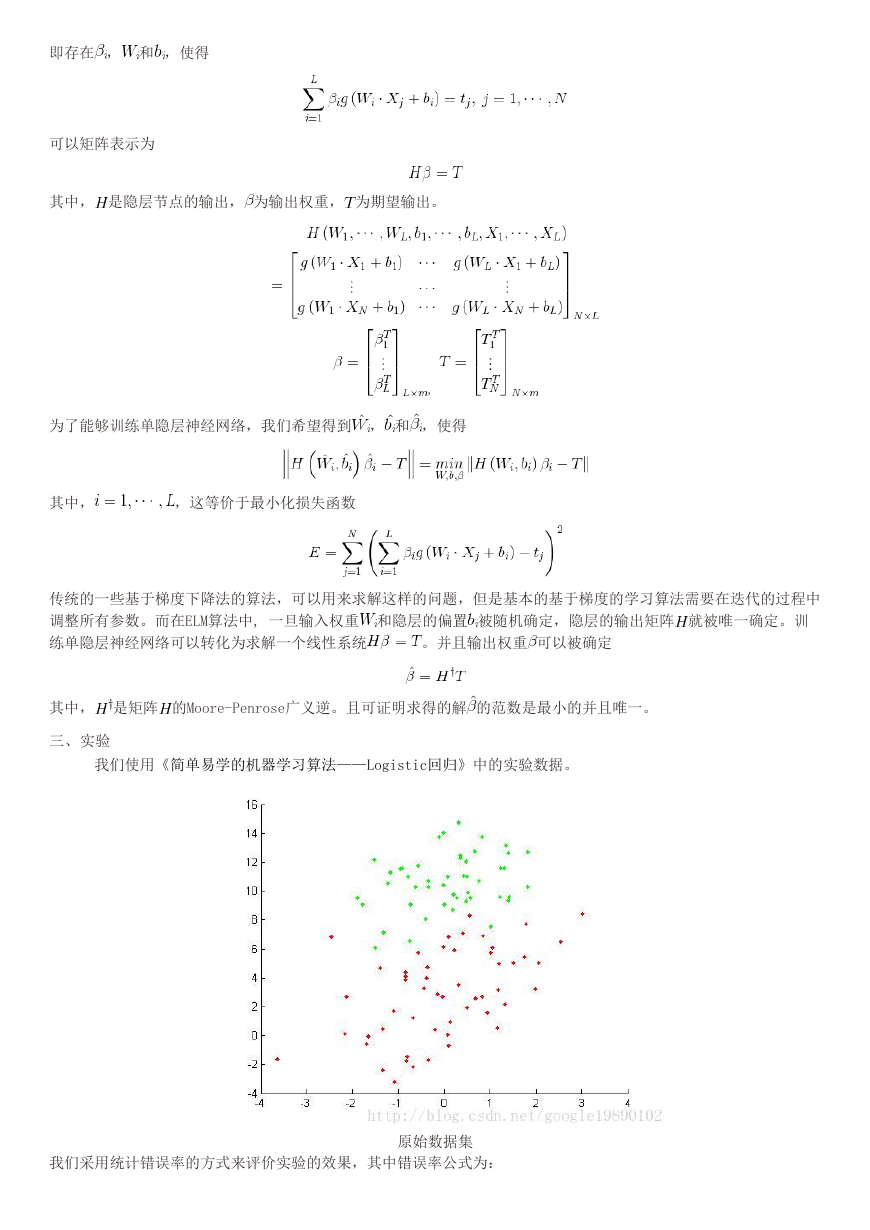
即存在 ， 和 ，使得 可以矩阵表示为 其中， 是隐层节点的输出， 为输出权重， 为期望输出。 为了能够训练单隐层神经网络，我们希望得到 ， 和 ，使得 ， 其中， ，这等价于最小化损失函数 传统的一些基于梯度下降法的算法，可以用来求解这样的问题，但是基本的基于梯度的学习算法需要在迭代的过程中 调整所有参数。而在ELM算法中, 一旦输入权重 和隐层的偏置 被随机确定，隐层的输出矩阵 就被唯一确定。训 练单隐层神经网络可以转化为求解一个线性系统 。并且输出权重 可以被确定 其中， 是矩阵 的Moore-Penrose广义逆。且可证明求得的解 的范数是最小的并且唯一。 三、实验     我们使用《简单易学的机器学习算法——Logistic回归》中的实验数据。 我们采用统计错误率的方式来评价实验的效果，其中错误率公式为： 原始数据集 

对于这样一个简单的问题， MATLAB代码 主程序 。 [plain]  %% 主函数，二分类问题      %导入数据集   A = load('testSet.txt');      data = A(:,1:2);%特征   label = A(:,3);%标签      [N,n] = size(data);      L = 100;%隐层节点个数   m = 2;%要分的类别数      %‐‐初始化权重和偏置矩阵   W = rand(n,L)*2‐1;   b_1 = rand(1,L);   ind = ones(N,1);   b = b_1(ind,:);%扩充成N*L的矩阵      tempH = data*W+b;   H = g(tempH);%得到H      %对输出做处理   temp_T=zeros(N,m);   for i = 1:N       if label(i,:) == 0           temp_T(i,1) = 1;       else            temp_T(i,2) = 1;       end       end   T = temp_T*2‐1;      outputWeight = pinv(H)*T;      %‐‐画出图形   x_1 = data(:,1);     x_2 = data(:,2);     hold on     for i = 1 : N         if label(i,:) == 0             plot(x_1(i,:),x_2(i,:),'.g');         else             plot(x_1(i,:),x_2(i,:),'.r');         end     end      output = H * outputWeight;   %‐‐‐计算错误率   tempCorrect=0;   for i = 1:N       [maxNum,index] = max(output(i,:));       index = index‐1;       if index == label(i,:);           tempCorrect = tempCorrect+1;       end   end      errorRate = 1‐tempCorrect./N;   01.  02.  03.  04.  05.  06.  07.  08.  09.  10.  11.  12.  13.  14.  15.  16.  17.  18.  19.  20.  21.  22.  23.  24.  25.  26.  27.  28.  29.  30.  31.  32.  33.  34.  35.  36.  37.  38.  39.  40.  41.  42.  43.  44.  45.  46.  47.  48.  49.  50.  51.  52.  53.  54.  55.  56.  57.  58.  59.  激活函数 [plain]  

01.  02.  03.  function [ H ] = g( X )       H = 1 ./ (1 + exp(‐X));   end   黄老师提供的极限学习机的代码：点击打开链接