功率谱估计性能分析及其MATLAB实现.docx-资料库

matlabfly-10520556-16359647276864376411.docx.pdf-第1页.png

第1页 / 共6页

matlabfly-10520556-16359647276864376411.docx.pdf-第2页.png

第2页 / 共6页

matlabfly-10520556-16359647276864376411.docx.pdf-第3页.png

第3页 / 共6页

matlabfly-10520556-16359647276864376411.docx.pdf-第4页.png

第4页 / 共6页

matlabfly-10520556-16359647276864376411.docx.pdf-第5页.png

第5页 / 共6页

matlabfly-10520556-16359647276864376411.docx.pdf-第6页.png

第6页 / 共6页

功率谱估计性能分析及其 MATLAB 实现一、经典功率谱估计分类简介 1．间接法根据维纳-辛钦定理，1958 年 Blackman 和 Turkey 给出了这一方法的具体实现，即先由 N 个观察值xN(n)，估计出自相关函数rx(m)，求自相关函数傅里叶变换，以此变换结果作为对功率谱Px(w)的估计。个观察值xN(n)直接进行傅里叶变换，得到XN(ejw)，然后取其幅值的平方，再除以 N，作为对功率谱Px(w)的估计。 Pper(w)，作为功率谱的估计，以此来改善用 N 点观察数据直接计算的周期图Pper(w)的方差将 N 点的观察值分成 L 个数据段，每段的数据为 M，然后计算 L 个数据段的周期图的平均 2．直接法 3．改进的周期图法直接法功率谱估计是间接法功率谱估计的一个特例，又称为周期图法，它是把随机信号的 N 特性。根据分段方法的不同，又可以分为 Welch 法和 Bartlett 法。 Welch 法所分的数据段可以互相重叠，选用的数据窗可以是任意窗。 Bartlett 法所分的数据段互不重叠，选用的数据窗是矩形窗。二、经典功率谱估计的性能比较 1．仿真结果为了比较经典功率谱估计的性能，本文采用的信号是高斯白噪声加两个正弦信号，采样率 Fs=1000Hz，两个正弦信号的频率分别为 f1=200Hz，f2=210Hz。所用数据长度 N=400. 仿真结果如下： 1

(a) (c) (e) (b) (d) (f) Figure1 经典功率谱估计的仿真结果 Figure1(a)示出了待估计信号的时域波形； Figure2(b)示出了用该数据段直接求出的周期图，所用的数据窗为矩形窗； Figure2(c)是用 BT 法（间接法）求出的功率谱曲线，对自相关函数用的平滑窗为矩形窗，长度 M=128，数据没有加窗； Figure2(d)是用 BT 法（间接法）求出的功率谱曲线，对自相关函数用的平滑窗为 Hamming 窗，长度 M=64，数据没有加窗； Figure2(e)是用 Welch 平均法求出的功率谱曲线，每段数据的长度为 64 点，重叠 32 点，使用的 Hamming 窗； Figure2(f)是用 Welch 平均法求出的功率谱曲线，每段数据的长度为 100 点，重叠 48 点，使用的 Hamming 窗； 2

2．性能比较 1) 直接法得到的功率谱分辨率最高，但是方差性能最差，功率谱起伏剧烈，容易出现虚假谱峰； 2) 间接法由于使用了平滑窗对直接法估计的功率谱进行了平滑，因此方差性能比直接法好，功率谱比直接法估计的要平滑，但其分辨率比直接法低。 3) Welch 平均周期图法是三种经典功率谱估计方法中方差性能最好的，估计的功率谱也最为平滑，但这是以分辨率的下降及偏差的增大为代价的。 3．关于经典功率谱估计的总结 1) 功率谱估计，不论是直接法还是间接法都可以用 FFT 快速计算，且物理概念明确，因而仍是目前较常用的谱估计方法。 2) 谱的分辨率较低，它正比于 2π/N，N 是所使用的数据长度。 3) 方差性能不好，不是真实功率谱的一致估计，且 N 增大时，功率谱起伏加剧。 4) 周期图的平滑和平均是和窗函数的使用紧密关联的，平滑和平均主要是用来改善周期图的方差性能，但往往又减小了分辨率和增加了偏差，没有一个窗函数能使估计的功率谱在方差、偏差和分辨率各个方面都得到改善，因此使用窗函数只是改进估计质量的一个技巧问题，并不能从根本上解决问题。三、 AR 模型功率谱估计 1．AR 模型功率谱估计简介 AR 模型功率谱估计是现代谱估计中最常用的一种方法，这是因为 AR 模型参数的精确估计可以用解一组线性方程（Yule-Walker 方程）的方法求得。其核心思想是：将信号看成是一个 p 阶 AR 过程，通过建立 Yule-Walker 方程求解 AR 模型的参数，从而得到功率谱的估计。由于已知的仅仅是长度有限的观测数据，因此 AR 模型参数的求得，通常是首先通过某种算法求得自相关函数的估计值，进而求得 AR 模型参数的估计值。常用的几种 AR 模型参数提取方法有： 1) 自相关法假定观测数据区间之外的数据为 0，在均方误差意义下使得数据的前向预测误差最小。由此估计的自相关矩阵式正定的，且具有 Toeplitz 性，可以用 Levison-Durbin 算法求解。 2) 协方差法不作观测数据区间之外的数据为 0 的假设，在均方误差意义下使得数据的前向预测误差最小。由此估计的自相关矩阵式半正定的，且不具有 Toeplitz 性，得到的 AR 模型可能不稳定。 3) 修正的协方差法不作观测数据区间之外的数据为 0 的假设，在均方误差意义下使得数据的前向预测误差与后向预测误差之和最小。由此估计的自相关矩阵式半正定的，且不具有 Toeplitz 性，得到的 AR 模型可能不稳定。但得到的一阶 AR 模型是稳定的。 3

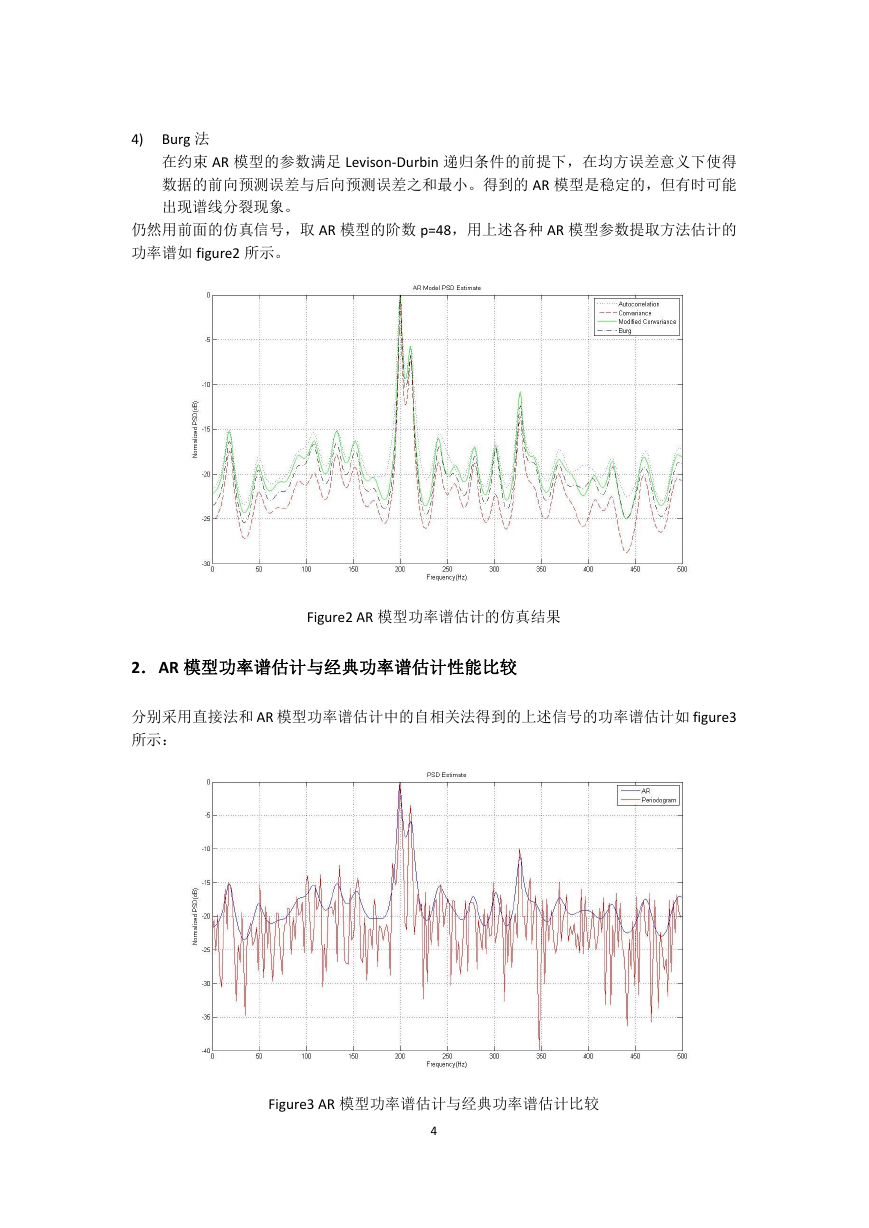
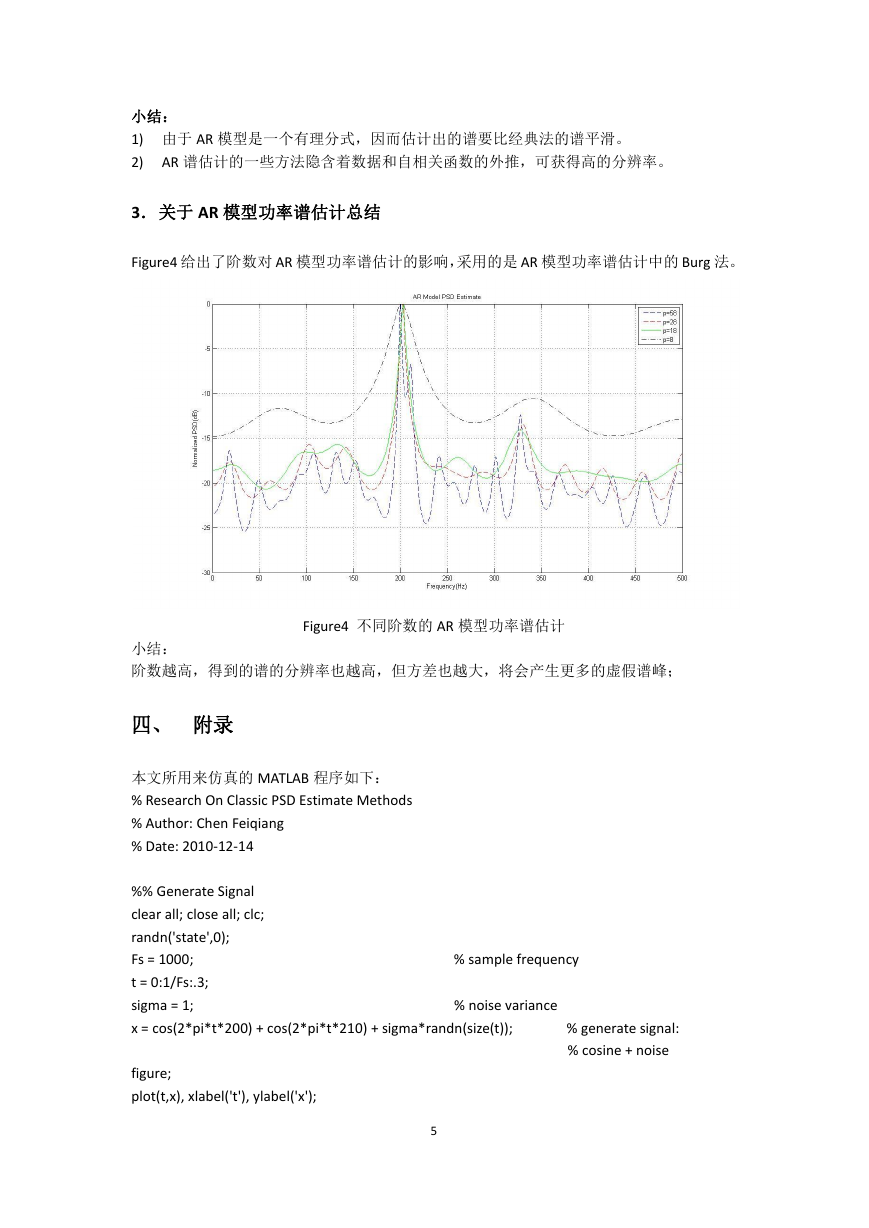
4) Burg 法在约束 AR 模型的参数满足 Levison-Durbin 递归条件的前提下，在均方误差意义下使得数据的前向预测误差与后向预测误差之和最小。得到的 AR 模型是稳定的，但有时可能出现谱线分裂现象。仍然用前面的仿真信号，取 AR 模型的阶数 p=48，用上述各种 AR 模型参数提取方法估计的功率谱如 figure2 所示。 Figure2 AR 模型功率谱估计的仿真结果 2．AR 模型功率谱估计与经典功率谱估计性能比较分别采用直接法和 AR 模型功率谱估计中的自相关法得到的上述信号的功率谱估计如 figure3 所示： Figure3 AR 模型功率谱估计与经典功率谱估计比较 4

小结： 1) 由于 AR 模型是一个有理分式，因而估计出的谱要比经典法的谱平滑。 2) AR 谱估计的一些方法隐含着数据和自相关函数的外推，可获得高的分辨率。 3．关于 AR 模型功率谱估计总结 Figure4 给出了阶数对 AR 模型功率谱估计的影响，采用的是 AR 模型功率谱估计中的 Burg 法。 Figure4 不同阶数的 AR 模型功率谱估计小结：阶数越高，得到的谱的分辨率也越高，但方差也越大，将会产生更多的虚假谱峰；四、附录本文所用来仿真的 MATLAB 程序如下： % Research On Classic PSD Estimate Methods % Author: Chen Feiqiang % Date: 2010-12-14 %% Generate Signal clear all; close all; clc; randn('state',0); Fs = 1000; t = 0:1/Fs:.3; sigma = 1; x = cos(2*pi*t*200) + cos(2*pi*t*210) + sigma*randn(size(t)); figure; plot(t,x), xlabel('t'), ylabel('x'); 5 % sample frequency % noise variance % generate signal: % cosine + noise

% window function used title('Signal In Time Domain');grid on; %% Estimate PSD using periodogram method window = rectwin(length(x)); xn = x'.*window; index = nextpow2(length(x)); N = pow2(index); Xw = fft(xn, N); Pw = Xw.*conj(Xw)/N; k = 0:floor(N/2 - 1); figure; plot(k*Fs/N, 10*log10(Pw(k+1)/max(Pw))); title('Periodogram PSD Estimate'); xlabel('Frequency(Hz)');ylabel('Normalized PSD(dB)'),grid on; hold on %% Estimate PSD using BT method window_a = rectwin(length(x)); % do N-points FFT % Calculate PSD % window function for data x(n) xn = x'.*window_a; Rx = xcorr(xn); N = length(Rx); M = floor(N/4); % M = 100; window_v = rectwin(M); RxWin = Rx(1:M).*window_v; function Pw = abs(fft(RxWin, N)); % auto-correlation function estimate % the length of smooth window % smooth window for BT method % smooth window multiply auto-correlation k = 0:floor(N/2 - 1); figure; plot(k*Fs/N, 10*log10(Pw(k+1)/max(Pw)),'r'); title('BT Method PSD Estimate'); xlabel('Frequency(Hz)');ylabel('Normalized PSD(dB)'),grid on; %% Estimate PSD using Welch method window = 32; noverlap = 8; nfft = pow2(nextpow2(length(x))); [Pxx,f] = pwelch(x,window,noverlap,nfft,Fs); figure; plot(f,10*log10(Pxx/max(Pxx)),'g'); title('Pwelch Method PSD Estimate'); xlabel('Frequency(Hz)');ylabel('Normalized PSD(dB)'),grid on; % the length of each segment % overlap number for each segment % nfft-points FFT for each segment % call pwelch function 6

资料库

功率谱估计性能分析及其MATLAB实现.docx

相关推荐

课程资源

热门标签

最新资料