2 2 　 第 9 期 2005 年 9 月 2 2 2 2 电 　　子 　　学 　　报 ACTA ELECTRONICA SINICA Vol. 33 　No. 9 Sep . 　2005 　 基于 keystone 变换的微弱目标检测 张顺生 ,曾 　涛 (北京理工大学电子工程系 ,北京 100081) 　　摘 　要 : 　提高雷达对微弱目标探测能力的主要方法是增加积累时间. 根据传统 PD 雷达的设计原则 ,在相参积 累时间内 ,目标的距离走动不能超过半个距离单元 ,也就是说相参积累时间受限于目标运动. 对于高距离分辨雷达或 观测高速目标的雷达系统 ,这种限制是很难满足的. 本文提出一种基于 keystone 变换的运动补偿方案 ,可以在没有目 标运动速度信息条件下校正距离走动 ,从而使积累时间不再受目标运动的限制. 关键词 : 　微弱目标检测 ; 相参积累 ; keystone 变换 ; 距离走动 中图分类号 : 　TN957 　　　文献标识码 : 　A 　　　文章编号 : 　0372 2112 (2005) 09 1675 04 Weak Target Detection Ba sed on Keystone Transform ZHANG Shun sheng ,ZENG Tao ( Department of Electronic Engineering , Beijing Institute of Technology , Beijing 100081 , China) Abstract : 　The improvement of the capability to detect moving target with very small radar signature is usually realized by long term accumulation. According to the design principle of conventional PD (Pulse Doppler) radar ,target’s range migration can’t exceed half of the range resolution cell in coherent integration time ,which means that the accumulation time is restrained by target’s motion. For high range resolution radar or the radar system focusing on the detection of fast moving targets ,such a restriction is difficult to sat isfy. In this paper ,a novel motion compensation method based on keystone transform is presented ,which can correct range migration without the exact value of target velocity ,and as a result ,make the accumulation time free of the restriction due to target motion. Key words : 　weak target detection ;coherent integration ;keystone transform ;range migration 1 　引言 　　随着隐身技术的日趋成熟 ,飞机 、导弹等目标的 RCS 减 小了一到两个数量级 ,极大地影响了雷达威力. 因此 ,对微弱 目标的 检 测 成 为 雷 达 急 需 解 决 的 技 术 问 题. 增 加 积 累 时 间 1 ,2 是提高雷达微弱目标检测能力的一种重要手段 ,但是 根据传统 PD 雷达的设计原则 ,在相参积累时间内 ,目标的距 离走动不能超过半个距离单元 ,也就是说相参积累时间受限 于目标运动. 对于高距离分辨雷达或观测高速目标的雷达系 统 ,这种限制尤为显著. 为了克服这个困难 ,在大多数情况下 都是利用长时间非相参积累的方法 3 ,4 提高信噪比 ,还有一 些学者把图像处理技术引入雷达信号检测领域. 例如 ,莫力 、 吴嗣亮 4 等提出了一种基于 Hough 变换的长时间积累方法 , 基本原理是把回波数据变换到距离 时间空间 ,在此 空间中匀速或匀加速目标回波表现为一条直线 ,这样目标检 测问题就转化为图像处理中的直线检测问题. 在文献 4 中 , 直线检测是通过 Hough 变换实现的. 用这种方法可以获得很 长的积累时间 ,但算法比较复杂 ,而且由于是非相参积累 ,积 累的效率不如相参积累. 多普勒 收稿日期 :2004 06 02 ;修回日期 :2005 03 28 　　本文通过 keystone 变换校正 PD 雷达的距离走动 ,然后进 行相参积累 ,达到提高信噪比的目的. 这种方法使相参积累时 间不再受目标运动的制约 ,从而使雷达系统设计更加灵活. keystone 变换是合成孔径雷达领域一种常用的距离走动校正 技术 5 ,但将它应用在 PD 雷达中 ,此前未见报道. 2 　分析 2 1 　keystone 变换的意义 合 成 孔 径 雷 达 (SAR) 的回波的支撑域 是一个二维平 面 , 平 面 的坐标轴分别是快时间 (即脉内时间) 和慢时间 (即脉间时间) . 在 快 时 间域进行傅立 叶 变 换 , 将回波变换到 f - tk 平 面. 所谓 keystone 变换就 是进行变量代换 : 

6761 　　电 　　子 　　学 　　报 2005 年 tk = f c τ f + f c (1) 这个变换使 f - tk 平面上的矩形支撑域在 f - τ平面上变 成一个倒梯形 ,如图 1 所示. 因为这种倒梯形和所谓 keystone 形状相似 ,keystone 变换因此得名. 可见 ,keystone 变换实际上 是一种对 tk 轴的伸缩变换 , 伸缩幅度和频率有关 , 高频拉伸 幅度较大. keystone 变换已被多位学者应用于动目标的合成孔 径雷达成像[5 ] ,具体成像算法不是本文关心的内容 ,这里不再 赘述. 2 2 　PD 雷达运动目标回波信号模型 对于常规雷达来说 ,当目标与雷达之间有相对运动时 ,进 行多普勒处理通常不考虑距离走动的影响. 然而 ,对于高分辨 的 PD 雷达 ,当目标与雷达之间存在相对运动时 ,就会发生距 离走动. 一般来说 ,雷达的距离分辨力越高 ,发生走动的现象 就越明显[6 ] . 下面从公式推导的角度来阐述距离走动的产生. 设 PD 雷达发射的基带信号为线性调频脉冲信号 : a ( t) = Rect t T0 exp ( jπbt2) (2) 这里 t 表示发射脉冲的时间变量 , T0 为发射脉冲宽度 , b 为调 频斜率. 由驻留相位原理[7 ] ,线性调频脉冲信号的频谱为 : A ( f ) = Rect f bT0 exp - j πf 2 b (3) 设在远处有一个匀速直线运动的点目标 , 它的基带回波信号 为 s ( t , n) : s ( t , n) = a ( t - τn) exp ( - j2πf cτn) exp ( j2πf dt) (4) 这里 n 为发射的脉冲个数 , f c 为载波频率 , f d 为多普勒频率 , R0 + vnT c τn = 2 为第 n 个脉冲的延迟时间 , R0 为 0 时刻的距 离 , v 为目标速度 ,远离方向为正 , T 为脉冲重复时间 ( PRT) . 则脉压后的信号频谱为 : f - f d/ 2 bT0 - f d exp [ - j2π( f + f c)τn ] 　X ( f , n) = Rect ·exp[ - j2πf dτn ]exp j2πf f d b exp - j πf 2 d b (5) 相应的时域信号为 : x ( t , n) = ( bT0 - f d) sin c ( bT0 - f d) ·exp jπf d t - τn + f d b ·exp[ - j2π( f c + f d)τn ]exp t - τn + f d b - j πf 2 d b (6) 从式 (6) 可以看出 :时域信号的包络是一个 sin c 函数. 由 sin c 函数性质知 ,信号峰值的位置位于 τn - f d/ d. 很明显 , 当 发射的脉冲不同时 ,回波的延迟时间亦不同 ,那么脉压后信号 峰值在相对距离轴上的位置不同 ,即发生了距离走动. 发射信 

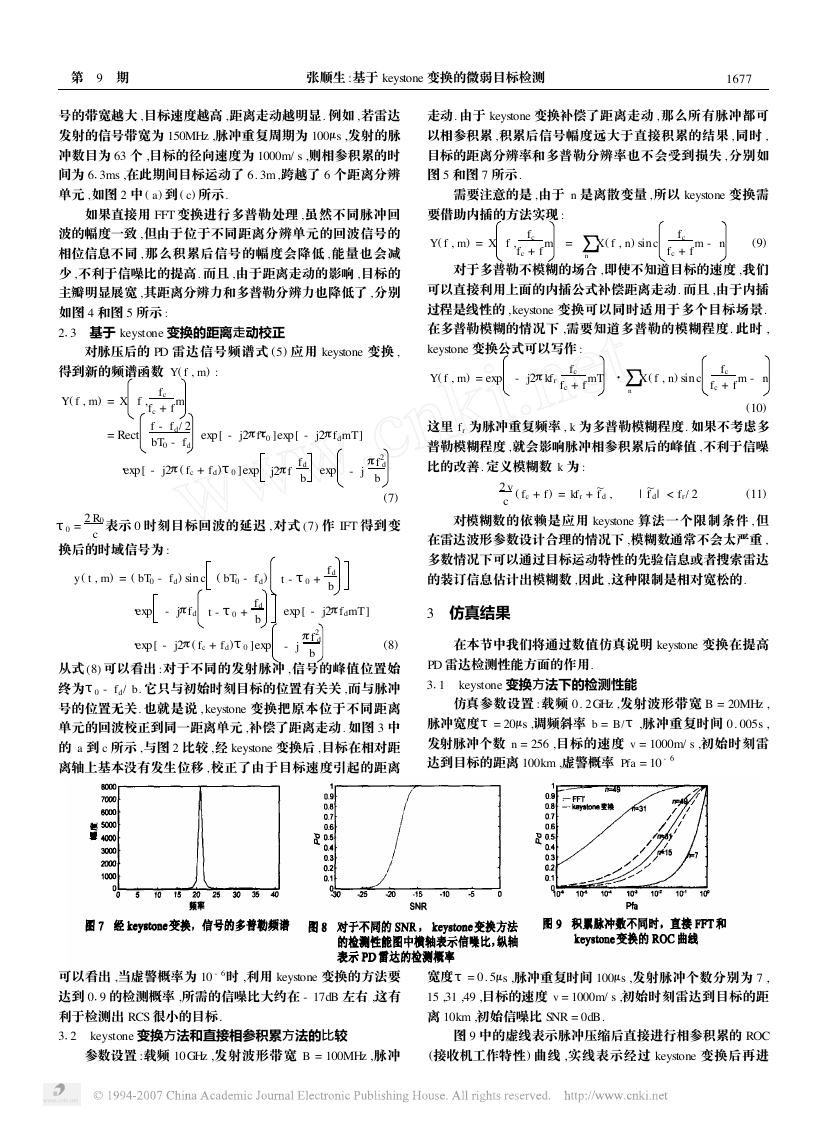
1 1 exp[ - j2πf dmT ] 3 　仿真结果 πf 2 d b - j (8) 从式 (8) 可以看出 :对于不同的发射脉冲 ,信号的峰值位置始 终为τ0 - f d/ b. 它只与初始时刻目标的位置有关关 ,而与脉冲 号的位置无关. 也就是说 , keystone 变换把原本位于不同距离 单元的回波校正到同一距离单元 ,补偿了距离走动. 如图 3 中 的 a 到 c 所示 ,与图 2 比较 ,经 keystone 变换后 ,目标在相对距 离轴上基本没有发生位移 , 校正了由于目标速度引起的距离 　　在本节中我们将通过数值仿真说明 keystone 变换在提高 PD 雷达检测性能方面的作用. 3 1 　keystone 变换方法下的检测性能 仿真参数设置 :载频 0. 2GHz ,发射波形带宽 B = 20MHz , 脉冲宽度τ= 20μs ,调频斜率 b = B/τ,脉冲重复时间 0. 005s , 发射脉冲个数 n = 256 ,目标的速度 v = 1000m/ s ,初始时刻雷 达到目标的距离 100km ,虚警概率 Pf a = 10 - 6 可以看出 ,当虚警概率为 10 - 6时 ,利用 keystone 变换的方法要 达到 0 9 的检测概率 ,所需的信噪比大约在 - 17dB 左右 ,这有 利于检测出 RCS 很小的目标. 3 2 　keystone 变换方法和直接相参积累方法的比较 参数设置 :载频 10GHz ,发射波形带宽 B = 100MHz ,脉冲 宽度τ= 0. 5μs ,脉冲重复时间 100μs ,发射脉冲个数分别为 7 , 15 ,31 ,49 ,目标的速度 v = 1000m/ s ,初始时刻雷达到目标的距 离 10km ,初始信噪比 SNR = 0dB. 图 9 中的虚线表示脉冲压缩后直接进行相参积累的 ROC (接收机工作特性) 曲线 ,实线表示经过 keystone 变换后再进 第 　9 　期 张顺生 :基于 keystone 变换的微弱目标检测 7761 号的带宽越大 ,目标速度越高 ,距离走动越明显. 例如 ,若雷达 发射的信号带宽为 150MHz ,脉冲重复周期为 100μs ,发射的脉 冲数目为 63 个 ,目标的径向速度为 1000m/ s ,则相参积累的时 间为 6 3ms ,在此期间目标运动了 6. 3m ,跨越了 6 个距离分辨 单元 ,如图 2 中 ( a) 到 ( c) 所示. 如果直接用 FFT 变换进行多普勒处理 ,虽然不同脉冲回 波的幅度一致 ,但由于位于不同距离分辨单元的回波信号的 相位信息不同 , 那么积累后信号的幅度会降低 , 能量也会减 少 ,不利于信噪比的提高. 而且 ,由于距离走动的影响 ,目标的 主瓣明显展宽 ,其距离分辨力和多普勒分辨力也降低了 ,分别 如图 4 和图 5 所示 : 2 3 　基于 keystone 变换的距离走动校正 对脉压后的 PD 雷达信号频谱式 (5) 应用 keystone 变换 , 得到新的频谱函数 Y ( f , m) : Y ( f , m) = X f , = Rect f c m f c + f f - f d/ 2 bT0 - f d exp[ - j2πfτ0 ]exp[ - j2πf dmT ] 　·exp[ - j2π( f c + f d)τ0 ]exp j2πf f d b exp - j πf 2 d b (7) 表示 0 时刻目标回波的延迟 , 对式 (7) 作 IFT 得到变 2 R0 c τ0 = 换后的时域信号为 : 　y ( t , m) = ( bT0 - f d) sin c ( bT0 - f d) t - τ0 + f d b ·exp - jπf d t - τ0 + f d b ·exp[ - j2π( f c + f d)τ0 ]exp 走动. 由于 keystone 变换补偿了距离走动 ,那么所有脉冲都可 以相参积累 ,积累后信号幅度远大于直接积累的结果 , 同时 , 目标的距离分辨率和多普勒分辨率也不会受到损失 , 分别如 图 5 和图 7 所示. 需要注意的是 ,由于 n 是离散变量 ,所以 keystone 变换需 要借助内插的方法实现 : Y ( f , m) = X f , f c f c + f m = ∑ n X ( f , n) sin c f c f c + f m - n (9) 对于多普勒不模糊的场合 ,即使不知道目标的速度 ,我们 可以直接利用上面的内插公式补偿距离走动. 而且 ,由于内插 过程是线性的 , keystone 变换可以同时适用于多个目标场景. 在多普勒模糊的情况下 ,需要知道多普勒的模糊程度. 此时 , keystone 变换公式可以写作 : f c f c Y ( f , m) = exp - j2πkf r mT ·∑ n f c + f X ( f , n) sin c m - n f c + f (10) 这里 f r 为脉冲重复频率 , k 为多普勒模糊程度. 如果不考虑多 普勒模糊程度 ,就会影响脉冲相参积累后的峰值 ,不利于信噪 比的改善. 定义模糊数 k 为 : 2 v c ( f c + f ) = kf r + f d , 　　| f d| < f r/ 2 (11) 对模糊数的依赖是应用 keystone 算法一个限制条件 , 但 在雷达波形参数设计合理的情况下 ,模糊数通常不会太严重 , 多数情况下可以通过目标运动特性的先验信息或者搜索雷达 的装订信息估计出模糊数 ,因此 ,这种限制是相对宽松的. 

2 1 　李海 ,吴嗣亮 ,莫力. 微弱信号长时间积累的检测方法 J . 北京 理工大学学报 ,2001 ,21 (5) :614 - 617. H Li ,S Wu ,L Mo. A method for long weak targets J . Journal of Beijing Institute of Technology ,2001 ,21 (5) :614 - 617. (Chinese Source) term signal integral detection of 2 　王俊 ,张守宏 ,杨克虎. 利用自适应子波变换提高弱运动目标的 检测性能J . 电子学报 ,1999 ,27 (12) :80 - 83. J Wang , S Zhang , K Yang. An improved coherent integration detector with adaptive wavelet transform J . Chinese Journal of Electronic , 1999 ,27 (12) :80 - 83. (Chinese Source) 3 　王俊 ,张守宏. 微弱目标积累检测的包络移动补偿方法 J . 电 子学报 ,2000 ,28 (12) :56 - 59. J Wang ,S Zhang , K Yang. Study on the motion compensation of range migration for weak moving target detectionJ . Chinese Journal of Elec tronic ,2000 ,28 (12) :56 - 59. (Chinese Source) 4 　Mo Li ,Wu Siliang ,Li Hai. Radar detection of range migrated weak tar term integration J . Chinese Journal of Electronics , get through long 2003 ,12 (4) :539 - 544. 5 　R P Perry ,R C Dipietro ,R L Fante ,SAR imaging of moving target J . IEEE Trans on AES ,1999. 35 (1) :188 - 200. 6 　Thomas L M , Elizabeth A M , Charles P P. Fast pulse Doppler radar processing accounting for range bin migrationJ . IEEE National Radar Conference ,1993. 264 - 266. 7 　Carrara W G, Goodman R S ,Majewski R M. Spotlight synthetic aper ture radar signal processing algorighms M . Boston : Artech House , 1995. 作者简介 : 张顺生 　男 ,1980 生于安徽怀宁 ,2002 年在 山东科技大学获得学士学位 ,现在北京理工大学 攻读博士学位 ,他的研究方向是 SAR 回波模拟 和 SAR 成像. E mail :2ss - 2001 @sina. com. 曾 　涛 　男 ,1971 年生于天津 ,1999 年在北 京理工大学电子工程系获得博士学位后留校任 教 ,现为该系副教授兼博士生导师 ,2002～2003 年 在英国伯明翰大学的电子和电器工程学院作访问 学者 ,他的研究方向是 SAR 成像和实时雷达信号 处理. 他已在国内外著名刊物上发表论文 20 多 篇 ,出版两本专著. E mail :zengtao @bit. edu. cn. 8761 　　电 　　子 　　学 　　报 2005 年 参考文献 : 行相参积累的 ROC 曲线. 可以看出 ,当积累的脉冲数比较少 时 ,由于距离走动很小 ,直接 FFT 方法的 ROC 曲线随着脉冲 数的增加而逐渐改善. 随着脉冲数的增加 ,目标走动跨越了几 个距离分辨单元. 当脉冲数分别 31 和 49 时 ,FFT 方法的两条 ROC 曲线基本重合. 也就是说 ,距离走动限制了积累脉冲数对 FFT变换方法的性能改善. 而对于 keystone 变换的方法 ,由于 补偿了距离走动 ,当积累脉冲数目增加时 ,keystone 变换方法 的优势也逐渐增加. 在本算例的参数条件下 ,当虚警概率为 10 - 6 ,脉 冲 数 n 为 49 时 , keystone 变 换 能 使 检 测 概 率 达 到 0. 945 ,而通过 FFT 方法获得的检测概率只有 0. 015. 3 　keystone 变换方法和 Hough 变换方法的比较 3 参数设置 :载频 0. 2GHz ,发射波形带宽 B = 20MHz ,脉冲 宽度τ= 20μs ,脉冲重复时间 0. 02s ,发射脉冲个数 n = 1024 , 目标的速度 v = 1000m/ s ,初始时刻雷达到目标的距离 400km. 图 10 中实线表 示 当 SNR = - 23dB 时 , 利 用 keystone 变 换方 法 得 到 的 ROC 曲线 ,带有星花的虚 线 表 示 当 SNR = - 16dB 时 , 通 过 Hough 变换方法得到 的 ROC 曲 线. 对 于 keystone 变换的方法 , 由经典的统计信号理论可以推导出检验统计量的表达式 ,利用 数值计算的方法绘制 ROC 曲线. 而对于 Hough 变换的方法 ,我 们无法推导其检验统计量的解析表达式 ,所以只能用蒙特卡罗 仿真的方法得到虚警概率和检测概率 ,然后绘出 ROC 曲线. 由 于蒙特卡罗仿真的次数只有 1000 次以及噪声的随机性 ,通过 Hough 变换的方法得到的 ROC 曲线不是很平滑. 从图中可以看 出两条曲线基本重合 ,但注意到 keystone 变换的输入信噪比比 Hough 变换法低了 7dB ,说明在本仿真参数条件下 ,keystone 变 换方法的灵敏度比 Hough 变换的方法大约高 7dB. 4 　结论 　　用 keystone 变换校正距离走动不需要知道目标速度的具 体信息 ,并且可应用于多个目标环境. 经过 keystone 变换 , PD 雷达的相参积累时间不再受目标距离走动的制约. 尽管积累 时间依然要受限于频综稳定性 、RCS 起伏和目标机动 ,但在许 多场合可以比传统 PD 雷达提高一到两个数量级 ,接近合成 孔径雷达的水平. 这将有效地改善雷达对微弱目标的检测能 力 ,同时由于积累时间的增加 ,雷达的多普勒分辨率大大提 高 ,为微多普勒分辨提供了途径 ,所以有希望应用于诱饵识别 领域.