2019--Topology optimization.pdf

发布时间：2022-06-08 发布人：admin 分类：说明书资料大小：3.52M 资料格式：pdf 举报版权申诉

weixin_43872565-11959521-4744302543424279990.pdf-第1页.png

第1页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第2页.png

第2页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第3页.png

第3页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第4页.png

第4页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第5页.png

第5页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第6页.png

第6页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第7页.png

第7页 / 共16页

weixin_43872565-11959521-4744302543424279990.pdf-第8页.png

第8页 / 共16页

Topology optimization of microchannel heat sinks using a two-layer model

1 Introduction

2 Two-layer heat sink model

2.1 Fluid dynamics modeling

2.2 Heat transfer modeling

3 Finite element formulation

4 Topology optimization problem

4.1 Material interpolation schemes

4.2 Problem formulation

4.3 Implementations

5 Case study

5.1 Optimized designs

5.2 Model validation

5.3 Influence of parameters

5.4 Designs at low pressure drops

5.5 Comparison with one-layer model

6 Conclusions

Declaration of Competing Interest

Acknowledgements

Appendix A Derivations of the two-layer heat sink model

A.1 Temperature profile in the thermal-fluid design layer

A.2 Reduction of the heat transfer equation for thermal-fluid design layer

A.3 Reduction of the heat transfer equation for substrate

References

International Journal of Heat and Mass Transfer 143 (2019) 118462 Contents lists available at ScienceDirect International Journal of Heat and Mass Transfer j o u r n a l h o m e p a g e : w w w . e l s e v i e r . c o m / l o c a t e / i j h m t Topology optimization of microchannel heat sinks using a two-layer model Suna Yan a,⇑,1, Fengwen Wang b, Jun Hong a, Ole Sigmund b a Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, School of Mechanical Engineering, Xi’an Jiaotong University, 710049 Xi’an, China b Department of Mechanical Engineering, Solid Mechanics, Technical University of Denmark, 2800 Kgs. Lyngby, Denmark a r t i c l e i n f o a b s t r a c t Article history: Received 2 April 2019 Received in revised form 4 July 2019 Accepted 20 July 2019 Available online 6 August 2019 Keywords: Microchannel heat sinks Two-layer heat sink model Temperature proﬁles Topology optimization Three-dimensional validation This paper investigates the topology optimization of microchannel heat sinks. A two-layer heat sink model is developed allowing to do topology optimizations at close to two-dimensional computational cost. In the model, reduced two-dimensional ﬂuid dynamics equations proposed in the literature based on a plane ﬂow assumption are adopted. By assuming a fourth-order polynomial temperature proﬁle of the heat sink thermal-ﬂuid layer and a linear temperature proﬁle in the substrate, two-dimensional heat transfer governing equations of the two layers are obtained which are thermally coupled through an out-of-plane heat ﬂux term. Topology optimizations of a square heat sink are carried out using the two-layer model. Comparison with a three-dimensional conjugate heat transfer analysis of optimized designs in COMSOL Multiphysics validates the accuracy of the two-layer model. The re-evaluation of an optimized design by a one-layer model commonly seen in the literature shows the inadequacy of the one-layer model in predicting physical ﬁelds properly. In addition, the inﬂuence of physical and opti- mization parameters on the layout complexity of optimized designs is studied and related to the Peclet number. Optimizations under diffusion-dominated conditions are performed and typical optimized topologies for heat conduction structures are seen. Ó 2019 Elsevier Ltd. All rights reserved. 1. Introduction Microchannel heat sinks have been attracting much attention since their introduction in [1] due to their high heat transfer per- formance. As pointed out by Tuckerman and Pease [1], microscopic channels provide very high heat transfer rate between ﬂuid and solid phases and thereby make effective and compact cooling of, e.g., integrated electric circuits possible. Cooled by a plate-ﬁn microchannel heat sink with optimized dimensions, the upper limit of power density of planar circuit arrays was increased nearly forty-fold compared to the suggested value at that time in [1]. Henceforth structural optimization of microchannel heat sinks has become an active research ﬁeld and much work has been done. As a simple yet effective optimization technique, sizing opti- mization has been widely applied to the optimization of microchannel heat sinks. Kim and Kim [2,3] conducted analytical heat transfer analysis of plate-ﬁn microchannel heat sinks by treat- ing the channels and ﬁns as a ﬂuid-saturated porous medium. The ⇑ Corresponding author. E-mail address: sunayan.me@gmail.com (S. Yan). 1 Part of this work was carried out while Suna Yan was a visiting student at Department of Mechanical Engineering, Technical University of Denmark. https://doi.org/10.1016/j.ijheatmasstransfer.2019.118462 0017-9310/Ó 2019 Elsevier Ltd. All rights reserved. velocity and temperature proﬁles were derived and the aspect ratio of channels and heat sink porosity were then optimized for mini- mizing the thermal resistance. Liu and Garimella [4] compared the accuracy and complexity of ﬁve heat transfer models of a plate-ﬁn heat sink and optimized the aspect ratio and porosity using a one-dimensional resistance model. The inﬂuence of ﬁn shape on heat transfer was investigated in [5–7] by simulating and comparing heat sinks with different ﬁn shapes. Readers are referred to the paper [8] for an overview of sizing and conﬁgura- tion optimizations of microchannel heat sinks. Different from sizing and conﬁguration optimizations where an a priori deﬁned structural topology is required, topology optimiza- tion has more design freedom and is well known to be able to pro- duce unintuitive optimized designs. Topology optimization was initially developed for the stiffness optimization of mechanical structures, consisting of computing the optimal distribution of an anisotropic material [9]. Density-based topology optimization approaches were developed later based on the use of material interpolations deﬁning the relations between isotropic material parameters and the density design variables. Examples of these material laws are the SIMP (Solid Isotropic Microstructure with Penalization) model [10,11] and RAMP (Rational Approximation of Material Properties) model [12]. Up to now, density-based

2 S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 Nomenclature u; P; T DP R T F u; P; T A AXd Ae C Da f f 1; f 2 f 3 gi H h k L Lc q q00 q00 q00 i R rmin T0 0 three-dimensional velocity vector, pressure and tem- perature pressure drop residual of governing equations boundary traction out-of-plane force two-dimensional velocity vector, rescaled pressure and temperature area of planar electric circuits design domain area area of element e heat capacity of ﬂuid Darcy number maximum volume fraction of ﬂuid thermal-ﬂuid layer velocity proﬁle and temperature proﬁle substrate temperature proﬁle inequality constraint half of thickness general heat transfer coefﬁcient thermal conductivity side length of heat sink characteristic length penalization parameter in material interpolation heat ﬂux heat ﬂux imposed on the bottom of the heat sink out-of-plane heat ﬂux at the interface thermal resistance radius of density ﬁlter inﬂow temperature Tb;max Ti Tmax um substrate maximum temperature temperature at the interface heat sink maximum temperature mean velocity inverse permeability design variable ﬂuid dynamic viscosity Greek symbols a c l /; x; u test functions in ﬁnite element analysis q0 s h ﬂuid density stabilization parameter non-dimensional temperature Superscripts h T u approximated ﬁeld in ﬁnite element analysis heat transfer analysis ﬂuid dynamic analysis Subscripts a SU; PS SUT b f k s t inverse permeability SUPG and PSPG stabilization for ﬂuid dynamics analysis SUPG stabilization for heat transfer analysis substrate ﬂuid thermal conductivity solid thermal-ﬂuid layer approaches have been widely applied in the optimization of differ- ent physical problems, including heat conduction problems [13,14], ﬂuid problems [15,16] and also multiphysics problems [17–19]. The design of heat sinks is a typical and challenging applica- tion of multiphysics topology optimization, where the distribu- tion of ﬂuid and solid is optimized by succesively solving the conjugate heat transfer problem and the optimization problem through up to hundreds of iterations. A large computational cost is therefore required. Parallel computation is essential to perform three-dimensional topology optimization of heat sinks, which has been applied to the design of natural convection heat sinks in [20,21]. On the other hand, to circumvent solving the full three-dimensional physical problems, different simpliﬁed heat transfer models have been developed in literature, especially for the topology optimization of heat sinks cooled by forced con- vection. A common engineering approach is to model the con- vection on the ﬂuid-solid interface based on the Newton’s law of cooling (NLC). The interface can be extracted by using hat functions [22,23] or level-set expressions [24]. Topology opti- mizations based on the NLC models do not require the ﬂow ﬁeld solution and hence the computational cost is reduced greatly. However, in the above NLC models a single constant convection coefﬁcient is assumed along the ﬂuid-solid interface and the coefﬁcient value is determined empirically. As discussed in [25], the fact that the interaction between structure and ﬂuid keeps changing during topology optimization and the optimized designs usually have unintuitive and unanticipated layouts makes it difﬁcult to justify the application the NLC models with empirically predetermined coefﬁcients. As the modeling of both solid and ﬂuid phases becomes neces- sary in the topology optimization of heat sinks, some two- dimensional conjugate heat transfer models are developed without considering the inﬂuence from the third dimension. In order to predict the ﬂuid ﬂow and the heat transfer throughout the design domain by a single system of equations, a velocity absorption term is introduced to the momentum equation as ﬁrst implemented by Borrvall and Petersson [15]. The velocity absorption term functions as a friction force applied only in the solid phase in these models. Hence, the ﬂow model is retained in the ﬂuid region while a van- ishing ﬂow is obtained in the solid region. Topology optimizations of microchannel heat sinks based on these two-dimensional mod- els have been carried out in the literature. Dede [26] performed topology optimization of a multipass branching microchannel heat sink by combining the designs optimized under different boundary conditions. Matsumori et al. [27] studied the topology optimiza- tion of microchannel heat sinks subject to a constant input power for driving the ﬂow. Topology optimizations of two-dimensional and three-dimensional microchannel heat sinks using level set boundary expressions were carried out in [28]. Multi-objective optimizations of heat sinks for balancing the heat transfer maxi- mization and pressure drop minimization were studied in [29,30]. Careful study on the pioneering work of Borrvall and Petersson [15] reveals that the velocity absorption term in effect represents the out-of-plane shear forces when reducing the three- dimensional ﬂow to two-dimensional based on the lubrication theory where a plane ﬂow is assumed. Therefore, the velocity absorption term never takes zero in the ﬂuid region for planar ﬂows, such as ﬂows of the heat sinks as considered. The methodology has been extended to the topology optimization of

S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 3 Navier-Stokes channel ﬂow problems in [16]. On the other hand, if the plane ﬂow assumption is abandoned, the generalized Stokes ﬂow model and Navier-Stokes ﬂow model developed in [15,16] respectively can still be applied to the topology optimization of three-dimensional ﬂow problems where the ﬂow is assumed inﬁ- nitely high. In this case, the shear force meaning of the velocity absorption term is lost and the generalized models become the Brinkman-type model for porous ﬂows. Thinking that the absorp- tion term was derived from a seemingly unrelated ﬂow condition for three-dimensional ﬂows, Guest and Prévost [31] proposed a Darcy-Stokes system which is more similar to the models adopted in the above two-dimensional topology optimizations of heat sinks with a zero friction force in the ﬂuid region. Regarding the heat transfer process, the heat ﬂux applied at the bottom of heat sinks is transferred to the ﬁns and ﬂuid through a conductive substrate which connects all the ﬁns and forms one of the surfaces of channels, as illustrated in Fig. 1(a). Numerical simulations of plate-ﬁn heat sinks have shown that assuming the heat ﬂux is imposed to the ﬂuid and solid phases evenly or to the solid phase only can result in an error of 50% and 24% respec- tively [4]. Therefore it is essential to take the redistribution of heat ﬂux in the substrate and the three-dimensional heat transfer effect into account in the modeing of microchannel heat sinks. McConnell and Pingen [32] introduced a thermal substrate below the thermal- ﬂuid layer in their heat sink model to enable heat transfer to occur in three dimensions in the topology optimization of heat sinks. This two-layer modeling approach was further developed by Haertel et al. and applied to the topology optimization of an air-cooled heat sink [33]. Considering that the air-cooled heat sink has a high aspect ratio while the substrate is quite thin, the conjugate heat transfer in the thermal-ﬂuid layer and the heat conduction in the substrate are modeled two-dimensionally, respectively. The ther- mal coupling between the two layers is represented through an out-of-plane heat ﬂux term which is determined by a design- dependent heat transfer coefﬁcient and the temperature difference between layers. To improve the accuracy of the two-layer model of air-cooled heat sinks, the bounds of the out-of-plane heat transfer coefﬁcient were determined according to three-dimensional simu- lations and one-dimensional thermal resistance analysis of a plate- ﬁn heat sink in [34]. Van Oevelen and Baelmans [35] proposed a two-layer model by averaging the governing equations over the height of the heat sink where the velocity and temperature proﬁles of the fully-developed plane ﬂow were used. However, the ﬂuid dynamics equations before averaging have in fact been reduced to two-dimensional ones with the velocity absorption term. The two-layer model was later used for the topology optimization of heat sinks in Stokes ﬂow to study the effect of ﬁltering techniques [36]. Inspired by the derivations of the reduced models of ﬂow problems in [15,16], a new two-layer model for microchannel heat sinks at low aspect ratios is developed in this paper to permit more convincing heat sink topology optimizations at close to two-dimensional computational cost. Keeping in mind that the channels of heat sinks under consideration are essentially planar, the reduced ﬂuid dynamics equations derived in [16] where the velocity absorption term takes a ﬁnite value in the ﬂuid phase are used but formulated in a different form. The temperature pro- ﬁles in the thermal-ﬂuid layer and substrate are derived by making suitable assumptions. By using the velocity and temperature pro- ﬁles, the reduced two-dimensional heat transfer equations for the two layers are obtained which are coupled through an out- of-plane heat ﬂux. The out-of-plane heat transfer coefﬁcient is evaluated based on the conservation of thermal ﬂow between lay- ers. The accuracy of the developed two-layer heat sink model is validated by comparing with the three-dimensional simulations of optimized designs at different layout complexities in COMSOL Multiphysics. The work in this paper is organized as follows. The two-layer model for microchannel heat sinks is developed in Section 2. Stabi- lized ﬁnite element formulation of the two-layer model is derived in Section 3. The overall topology optimization problem is formu- lated in Section 4 and implementation details are also covered. Topology optimizations of a square microchannel heat sink are performed in Section 5 and the proposed two-layer model is veri- ﬁed in this section. Discussion and conclusions are given in Section 6. 2. Two-layer heat sink model A sketch of a microchannel heat sink as considered in this work is shown in Fig. 1(a) which has much larger x-y in-plane dimen- sions than its height. For the goal of deriving the two-layer model, the heat sink is viewed as a layered structure, consisting of the low conductive cover plate, the thermal-ﬂuid layer and the highly con- ductive substrate. The cover plate is thermally insulated and together with the substrate conﬁne the ﬂuid ﬂow to the thermal- ﬂuid layer. The bottom surface of the substrate, where electrical circuits are attached, is assumed uniformly heated. The imposed heat ﬂux is re-distributed in the substrate and transferred up to the thermal-ﬂuid layer in the manners of conduction and convec- tion. Fluid ﬂowing across the thermal-ﬂuid layer carries heat away through convection over solid ﬁns and substrate. Under suitable assumptions, the ﬂow velocity u and temperatures in both layers Tt; Tb have invariant proﬁles in the ﬂow direction as depicted in Fig. 1(b) and explained in the following. By applying these invari- ant proﬁles, the thermal-ﬂuid layer and substrate can be modeled two-dimensionally and heat is transferred from the substrate to the thermal-ﬂuid layer via a virtual interface as shown in Fig. 1(c). By doing topology optimization, the distribution of ﬂuid and solid materials, in the thermal-ﬂuid layer (design layer) is optimized to improve the heat transfer performance of the heat sink. For the analysis of heat sinks, the following assumptions are introduced: (1) the ﬂuid constitutes a laminar and incompressible ﬂow; (2) the ﬂuid ﬂow and heat i.e., the layout of channels and ﬁns, Fig. 1. A microchannel heat sink as studied in this work. (a) Three-dimensional sketch, (b) Cross-section of the heat sink along the ﬂow direction and proﬁles of the three- dimensional ﬂow velocity u, thermal-ﬂuid layer temperature Tt and substrate temperature Tb. Here, kuk is the magnitude of the velocity vector on the mid-plane of the design layer, Tt is the ﬂuid bulk mean temperature, T b is the mean temperature of the substrate and Ti is the temperature at the interface. (c) The two-layer heat sink model.

4 S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 transfer are in steady-state; (3) the material properties of ﬂuid and solid phases are constant and do not change with temperature. The ﬂuid ﬂow is further assumed to be hydrodynamically and ther- mally fully developed in the derivation of the two-layer heat sink model. the resulting two-dimensional weak formulations, reduced and rescaled heat transfer governing equations of the two layers are then obtained. In the following, the derived temperature proﬁles and reduced heat transfer governing equations are given directly for simplicity. Detailed derivations can be found in Appendix A. 2.1. Fluid dynamics modeling ð Þ; As the ﬂuid ﬂow is hydrodynamically developed and the design layer has much larger in-plane dimensions than its height, the ﬂow is simpliﬁed as a Poiseuille ﬂow between two parallel plates. The ﬂow velocity proﬁle along the height of design layer is then a para- bola and does not change in the ﬂow direction, i.e., 2 ¼ f 1 zð Þ u1e1 þ u2e2 u f 1 zð Þ ¼ 1 z T is the where, u is the three-dimensional velocity vector, u ¼ u1; u2 velocity vector deﬁned on the mid-plane of design layer, e1 and e2 are two of the standard basis vectors for the three-dimensional Cartesian coordinate system, Ht is half of the height of design layer and z 2 Ht; Ht ð1Þ . Ht ½ ½ u ÞT ð2Þ 5l 2H2 t 0u ru ¼ rP þ lr ru þ ruð By using the velocity ﬁeld representation in Eq. (1) and assum- ing uniform pressure ﬁeld in z direction, the reduced two- dimensional continuity and momentum equations deﬁned on the x-y plane for the ﬂow in the design layer have been derived in [15,16], which are r u ¼ 0 q 6 7 0 and l are the ﬂuid density and dynamic viscosity, respec- where, q tively and P represents a rescaled in-plane pressure ﬁeld. The three- dimensional velocity ﬁeld and pressure ﬁeld can be retained using the relations u ¼ f 1 zð Þ u; 0½ The third term on the right side of the reduced momentum equation F ¼ au where a ¼ 5l models the effect of the out-of-plane shears in ﬂuid ﬂow. As the material distribution in the design layer is changing during topology optimization, the reduced governing equations should be able to model not only the Poiseuille ﬂow in the ﬂuid region but also the vanishing ﬂow in solid region. Hence, the inverse permeability a is extended to be a function of the design variable ﬁeld c, the formulation of which is detailed in Section 4.1. In the ﬂuid region where c ¼ 1, the factor a takes its smallest value and the force term F retains the out-of-plane shear effect, while in the solid region where c ¼ 0, a very large a is attained to penalize the ﬂow and obtain a vanishing ﬂow velocity. T and P ¼ 4P 5= . . 2H2 t 2.2. Heat transfer modeling Similar to the reduction of ﬂuid dynamics equations, the heat transfer equations can also be reduced to two-dimensional by using the temperature proﬁle formulations of the heat sinks. On the other hand, the heat transfer process involves both the thermal-ﬂuid layer and substrate. Hence the thermal coupling between the two layers is considered after the investigation of each layer to couple the reduced governing equations to one sys- tem. Speciﬁcally, a fourth-order polynomial temperature proﬁle and a linear temperature proﬁle are derived for the thermal-ﬂuid layer and substrate respectively as depicted in Fig. 1(b). Substitut- ing the temperature proﬁles and the velocity proﬁle into the weak formulations of the heat transfer equations and then integrating, the dependency of the formulations on z dimension can be elimi- nated and some rescaling constants are introduced. By localizing 4 6 z ¼ f 2 zð Þ; Considering that the ﬂuid ﬂow is hydrodynamically and ther- mally developed and assuming the heat ﬂux applied at the bottom of ﬂow is constant, then the proﬁle of the non-dimensional tem- perature variable deﬁned below is invariant in the ﬂow direction [37]. ht ¼ TiTt TiTt f 2 zð Þ ¼ 35 design layer, Tt ¼R ture of the ﬂuid, um ¼R where, Tt represents the three-dimensional temperature ﬁeld of is the bulk mean tempera- is the mean velocity of the ﬂow, Ti is the temperature at the interface between thermal-ﬂuid layer and substrate and z 2 Ht; Ht kukTt dz 2Htum Þ kukdz 2Ht Þ HtHt ½ . 2 þ 8 z þ 13 ð3Þ HtHt ð = ð = z Ht 416 Ht Ht The two-dimensional heat transfer governing equation for the thermal-ﬂuid design layer is derived based on the temperature proﬁle Eq. (3) as ð ð Þ ¼ 0 Þ 49 52 r ktrTt 0C u rTt ð q Þ 1 2Ht ht Ti Tt ð4Þ 2 3 where, C is the heat capacity of ﬂuid, kt ¼ kt cð Þ is the effective ther- mal conductivity and its formulation is deﬁned in Section 4.1 which in ﬂuid region and that of solid equals the ﬂuid conductivity kf material ks in ﬁns. The ﬂuid bulk mean temperature Tt is the state variable in this reduced two-dimensional governing equation. q00 is an out-of-plane heat ﬂux i which shows the thermal coupling between thermal-ﬂuid layer and substrate. Þ with ht ¼ 35kt 26Ht ¼ ht Ti Tt ð = ð Þ The three-dimensional heat conduction governing equation for the substrate is reduced based on the following non-dimensional temperature variable whose proﬁle is invariant in x-y directions. hb ¼ TiTb ¼ f 3 zð Þ; TiTb f 3 zð Þ ¼ 1 z substrate, Tb ¼R HbHb where, Tb represents the three-dimensional temperature ﬁeld of is the mean temperature and equals the temperature at the mid-plane of substrate for the linear temper- ature proﬁle used here, Hb is half of the height of the substrate and z 2 Hb; Hb ½ The two-dimensional heat conduction governing equation for Tb dz 2Hb ð5Þ ð = . Hb Þ the substrate is derived as kb 2 r2Tb þ 1 2Hb hb Tb Ti ð Þ q00 0 2Hb ¼ 0 ð6Þ where, kb ¼ ks is the thermal conductivity of the solid material, q00 0 is the heat ﬂux applied on the bottom surface of the substrate. The mean temperature Tb is the state variable in the reduced governing Þ with equation. The out-of-plane heat ﬂux q00 hb ¼ kb Hb= also represents the heat transfer from substrate to thermal-ﬂuid layer. ¼ hb Tb Ti ð i ð Using the concept of thermal circuits, the heat ﬂux representing the thermal coupling between layers can also be expressed as Þ ¼ h Tb Tt q00 . As the effective thermal i is design-dependent conductivity of the thermal-ﬂuid layer kt and equals that of the ﬂuid and solid materials at corresponding regions, the general heat transfer coefﬁcient h is much higher in Þ, where h ¼ hthb ht þ hb ð =

S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 Z Z ! Z 0C uh h 2Ht Z 2 3 Xt q Z Xnel Xt þ @Th t @xj uh t uh j t Th b sSUT uh j e¼1 Xe t kb 2 Z @uh @Th b b @xj @xj bdX q00 uh 0 2Hb dX þ Xb Xb Cq b dX Th @uh t @xj kt @Th t @xj @uh t @xj t q00 uh t dC dX ¼ 0 ; Th b t Th t dX t Cq t Z 49 52 dX þ Xt dX RT uh; Th h b Th b 2Hb bdC ¼ 0 bq00 uh uh Xb Z Z 2 2 3 52 2Hb Þ 49 Þ ¼ 0 q kb ð Tb Tt Þ h 2Ht ¼ 0 ﬁns than in ﬂuid regions. The out-of-plane heat ﬂux q00 i can thus ﬂexibly represent the conductive and convective heat transfer between the thermal-ﬂuid layer and substrate. The system of reduced two-dimensional governing equations for the heat trans- fer in the heat sink are r ktrTt ð Þ q00 Tb Tt ð 0 2Hb 0C u rTt ð r2Tb þ h In summary, the governing equations of the heat transfer process of (2) and (7), respectively. The system is weakly coupled in the sense that the ﬂow ﬁeld is independent of the temperature ﬁeld, whereas the temperature ﬁeld is inﬂuenced by the ﬂow ﬁeld due to the convection effect. The dependency of material inverse permeability a, effective thermal conductivity kt and heat trans- fer coefﬁcient h on the design variable ﬁeld c enables the description of ﬂow regions and solid regions using the same set of equations. the heat sinks under consideration are Eqs. ð7Þ 3. Finite element formulation The computational domain consisting of thermal-ﬂuid design layer and substrate is discretized by 4-node quadrilateral ﬁnite ele- ments. When the standard Galerkin ﬁnite element formulation is used, two main sources of numerical instabilities may occur. One is oscillations in the pressure ﬁeld caused by inappropriate pairs of velocity and pressure interpolations which violate the Ladyzhenskaya-Babuska-Brezzi (LBB) stability condition. The other is the occurrence of node-to-node oscillations, ‘wiggles’, in velocity ﬁeld and temperature ﬁeld emanating from the steep solution gra- dient especially in convection dominated problems. Therefore, the pressure-stabilizing/Petrov-Galerkin and streamline-upwind/Petrov-Galerkin (SUPG) term [39] are added to the weak form of governing equations to construct stabilized ﬁnite element formulation. The PSPG term helps circumvent the LBB condition and hence the computationally desirable equal- order velocity and pressure interpolations become viable. The SUPG term solves the wiggle problem by adding a proper amount of diffusion in the ﬂow direction which can also be viewed as a streamline upwind perturbation to the weighting functions. term [38] (PSPG) The stabilized weak forms for the continuity and momentum equations given by Eq. (2) are ð e¼1 Z Xnel dX þ Z Xe t @/h @xi sPS Þ 6q 0 7= Z Ru dX ¼ 0 i uh; Ph Pdij þ l @ui @xj @xh i @xj j Xt Xt Xe t þ e¼1 6 7 xh Z q 0 dX xh i axh Xt þ þ @uj @xi dX ¼ 0 T idC Ru i uh; Ph @uh Z i uh i j @xj i dX i uh Xnel sSU uh where, Xt ¼Pnel Ph are the approximated velocity ﬁeld and pressure ﬁeld respec- tively, xh ¼ xh ; xh 1 2 ary traction, Ru i uh; Ph is the residual form of the momentum equation, sPS is the PSPG stabilization parameter, sSU is the SUPG stabilization parameter for the momentum equation. Ch @xh ð9Þ i @xj T and t represents the design layer, uh ¼ uh Xe T and /h are the test functions, T i is the bound- ; uh 2 e¼1 1 The stabilized formulation for the convection-diffusion equa- tion in design layer and the standard Galerkin formulation for the heat conduction equation in the substrate are Z Z /h @uh i @xi Xt dX þ ð8Þ 5 ð10Þ ð11Þ t and Th where, Xb denotes the substrate domain, Th b are the approx- imated temperature ﬁelds of the design layer and substrate respec- t and q00 t and uh tively, uh b are boundary heat ﬂuxes, RT uh; Th form of the convection- diffusion equation and sSUT is the corresponding SUPG stabilization parameter. b are test functions, q00 ; Tb is the residual t t local length scales and velocity scales. Here, The stabilization parameters play an important role in the sta- bilized ﬁnite element method and their values are usually a func- tion of the formulations of stabilization parameters proposed in [40] and extended in [25] are used, where the local length scales are decided based on the local solution gradients and the local material inverse permeabilities are also taken into account in computing the parameters for the ﬂow equations. Hence, the ﬂow equations are non-linear with respect to the velocity ﬁeld due to the convection term and also the stabilization parameters sSU and sPS. The thermal equations are implicitly non-linear with respect to the tempera- ture ﬁeld due to the stabilization parameter sSUT . 4. Topology optimization problem 4.1. Material interpolation schemes In topology optimization the design of structures is represented by material distribution, i.e., the design variable ﬁeld which is denoted here as c. Speciﬁcally for the design of the heat sinks under consideration, the material at each point x in design domain is either ﬂuid with c xð Þ = 1 or solid with c xð Þ ¼ 0. The topology optimization of heat sinks usually requires at least several hun- dreds of iterations to obtain a good design. In addition, the govern- ing Eqs. (8)–(11) are non-linear and should be solved through an iterative procedure. Mathematically well-founded and efﬁcient gradient-based optimization algorithms therefore should be used, which require the design variables to be continuous in the range of 0; 1½ . The physical meaning of design variables can then be understood as the volume fraction occupied by ﬂuid at each point. RAMP-style interpolations [12,15] are used to deﬁne the material property-to-design variable relations. The inverse permeability a is formulated as a cð Þ ¼ as þ af as ð12Þ c 1 þ qa c þ qa where, af and as are the inverse permeabilities of ﬂuid and solid regions respectively and qa is a penalization parameter which is used to suppress intermediate values of design variables, since the ﬁnal goal of topology optimization is to obtain discrete-valued designs. As discussed in Section 2.1, the force term F ¼ au should retain the out-of-plane shear stress in the ﬂuid region, thus af ¼ 5l is used and Ht is half of the channel height. As . 2H2 t

6 S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 h . for the solid region, a zero channel height should be used in theory. But for implementation purposes, a very small channel height . The same Ht 100 ratio between as and af is also used in [16]. is used instead and thus as ¼ 5l 2 Ht=100 Þ2 i ð = The effective thermal conductivity kt is interpolated as kt cð Þ ¼ kf þ ks kf 1 c 1 þ qkc ð13Þ where, kf and ks are the thermal conductivities of ﬂuid and solid respectively and qk is a penalization parameter to suppress interme- diate design variables through the effect on material thermal con- ductivity. Based on the interpolation of the effective thermal conductivity, the relation of heat transfer coefﬁcient between layers and design variable h ¼ h cð Þ can be readily obtained. In density-based topology optimization approaches, the design variable ﬁeld is also discretized by the ﬁnite element mesh and each element is assigned with a unique design variable. Hence, the design of the heat sink is represented by the design variable vector c. As the material inverse permeability and effective thermal conductivity are interpolated as functions only depending on the design variable ﬁeld, they are also represented by the correspond- ing vectors and can be substituted in the stabilized formulations (8)–(11). where, N is the total number of substrate nodes and Tb;i is the tem- perature of node i. The value of the temperature norm parameter p should be able to capture the trend of maximum temperature in the optimization process and also ensure adequate smoothness of the objective function. Based on the studies in [13,41,42] on the effect of the norm parameter, p ¼ 10 is used in our work. The volume constraint in topology optimization problems is usually used for the consideration of material cost or structural weight to avoid optimized designs made of the better material completely. In the design of forced-convection heat sinks, however, a trade-off between increasing the convection surface and reducing the ﬂow resistance is expected in the optimized designs. Therefore, optimized heat sinks should not be blank without any ﬁns or solid blocks without any channels even if no volume constraint is applied, when appropriate boundary conditions are applied, e.g., the allowable pressure drop is large enough. On the other hand, the volume constraint also works together with the penalized material interpolation schemes to suppress intermediate design variables and it avoids congestion in the design domain. For heat sinks design, the increase in ﬂow resistance also helps suppress intermediate design variables to some extent. A trivial volume con- straint is thus used in most cases of this work by setting f ¼ 1 unless otherwise stated. 4.2. Problem formulation 4.3. Implementations The heat transfer performance of a heat sink can be measured by its thermal resistance, which is deﬁned as ð14Þ R ¼ Tmax T0 q00 0A where, q00 0 is the heat ﬂux imposed by the planar electric circuits which are attached to the substrate and have an area of A; q00 0A is then the power to be dissipated by the heat sink, T0 is the input coolant temperature, Tmax is the maximum temperature of the heat sink which is expected to appear in the substrate. As q00 0A and T0 are usually ﬁxed, the maximum temperature of the substrate is selected as the objective function in the topology optimization of heat sinks in this work. The topology optimization problem is then formulated as min : Tb;max equillibrium equations 8ð Þ 11ð Þ; Xnd c eAe 6 fAXd ; e¼1 gi cð Þ 6 0; 0 6 c 6 1: i ¼ 1; . . . ; m ð15Þ c s:t: : where, Tb;max is the maximum temperature of the substrate, AXd is the area of design domain Xd which is a subset of the design layer and discretized into nd elements, c e is the design variable of element e and Ae is the elemental area, the ﬁrst inequality hence constrains the volume fraction of ﬂuid to be no larger than f in the design domain. Whether or not other inequality constraints gi cð Þ are needed depends on the problems under consideration and the requirements of designers. An example is when the inﬂow velocity distribution is prescribed, an additional pressure drop constraint may be applied to limit the power necessary to drive ﬂow through the heat is non- differentiate, Tb;max is approximated by the generalized p-norm of the substrate nodal temperatures as sink. Considering that the max-operator Tb;max 1 N XN i¼1 Tp b;i !1=p ð16Þ To avoid checkerboards in and mesh dependency of design results, the density ﬁltering technique [43,44] is applied. The element-wise design variables are replaced by the weighted aver- age of design variables of their neighbours within a mesh- independent region deﬁned by the ﬁlter radius rmin. The ﬁltered design variables are the ones with physical meaning and used to compute material properties by Eqs. (12) and (13). The distribution of ﬂuid and solid is optimized by using the Method of Moving Asymptotes (MMA) [45] as the optimization algorithm. Sensitivities of the objective function and volume con- straint with respect to the design variables are computed based on the adjoint approach. As in [25], the dependency of stabilization parameters on velocity and temperature ﬁelds is neglected in com- puting the sensitivities. The accuracy of these approximate sensi- tivities are validated through ﬁnite difference checks. The optimization procedure is considered converged when the maximum change of design variables from iteration to iteration is smaller than a certain value (0.01 in this work). In addition, the optimization is allowed to run a maximum of 250 iterations. To end up with better optimized designs, a continuation approach to gradually increase the penalization parameter(s) is adopted. Speciﬁcally, is every 50 iterations or upon updated in a sequence of 1; 3; 10; 30 convergence, while the penalization parameter on inverse perme- ability is ﬁxed at qa ¼ 0:1. After optimization, the results are pro- jected to obtain strictly black-white designs by a simple threshold projection satisfying the volume ratio of ﬂuid and solid phases. the penalization on effective conductivity qk ½ 5. Case study Topology optimization of a square heat sink is performed in this section using the proposed two-layer model and methodology. The heat sink is sketched in Fig. 2, where a square substrate is cooled by a thermal-ﬂuid design layer which has a square ﬂow domain and additional inlet and outlet regions. Normal ﬂow is speciﬁed at inlet and outlet boundaries and other boundaries of the design layer satisfy the no-slip boundary condition. The pressure drop of the heat sink is prescribed and imposed by setting T 1 ¼ DP and

S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 7 Fig. 2. The square heat sink for topology optimization is sketched in (a). The two different design domain settings are illustrated in (b) and (c). 0 ¼ 6 104W m2 T 1 ¼ 0 at the inlet and outlet boundaries, respectively, where T 1 denotes the boundary traction in the x-direction. A constant heat ﬂux q00 is applied over the bottom of the substrate. The inlet coolant temperature is ﬁxed at T0 ¼ 0 °C, while other boundaries of the heat sink are thermally insulated. Water is used as the coolant and silicon is the material of the substrate and ﬁns. Material properties and dimensions of the heat sink are listed in Table 1. As the change of material properties with temperature is not considered in the following case studies, the problem is linear with respect to the heat ﬂux q00 0 and scaling of the heat ﬂux will not change the design results. Considering that the heat sink and the loading and boundary conditions are symmetric with respect to the horizontal central line, only the upper half of the heat sink is considered in topology optimization and a symmetric boundary condition is applied on the central line. The half of the square region in the design layer is discretized into 440-by-220 elements and the same for the sub- strate. The inlet and outlet regions are discretized into 110-by-55 elements, respectively. A ﬁlter radius of rmin ¼ L 100 is used in the density ﬁltering, where L is the side length of the square ﬂow region. Two different settings of design domain are used, as illus- trated in Fig. 2. In the ﬁrst setting, only the square ﬂow region is designable and the inlet and outlet are speciﬁed to be ﬂuid, while in the second one the outlet and part of the inlet away from the inﬂow boundary are also allowed to be optimized. The initial guess for topology optimizations is c ¼ 0:9 in the square ﬂow region and c ¼ 1 in inlet and outlet regions. = 5.1. 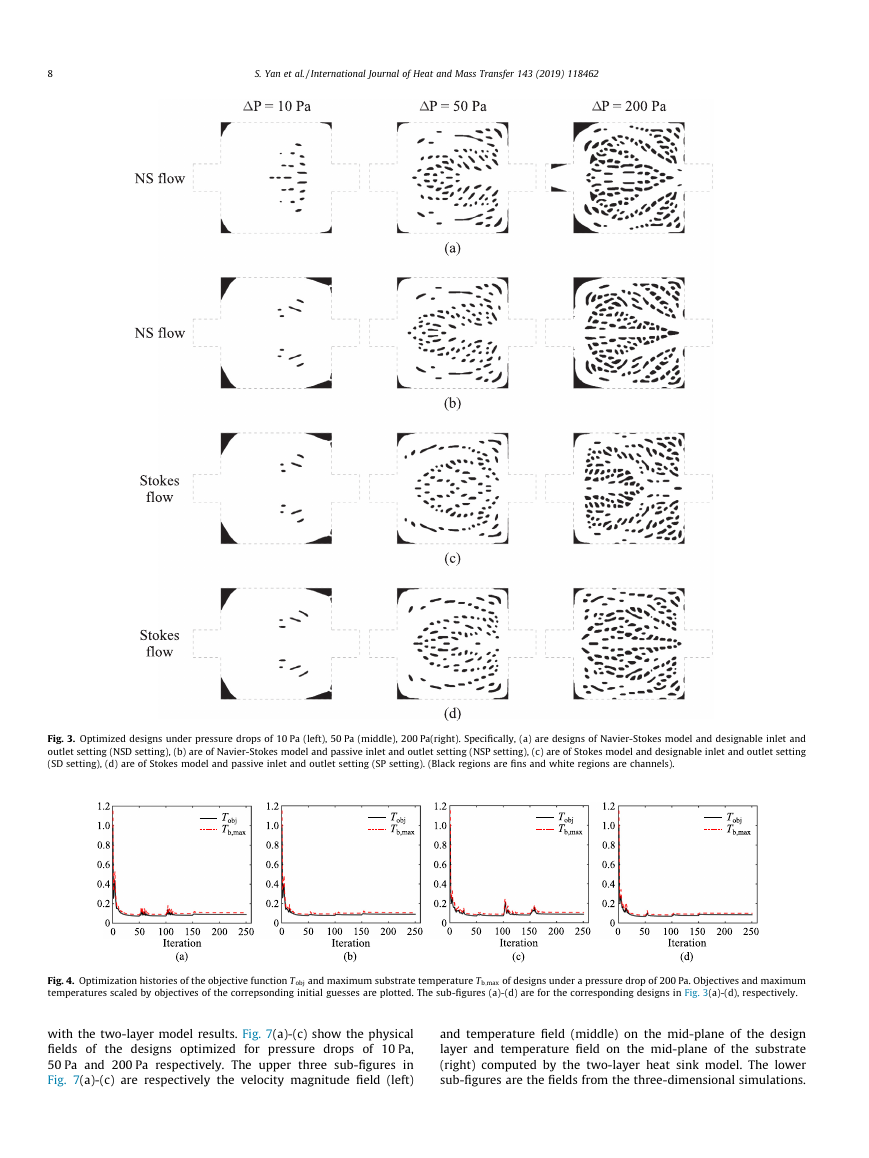Optimized designs Topology optimizations of the heat sink have been done using different pressure drop values (DP = 10 Pa, 50 Pa, 200 Pa), ﬂow models (Navier-Stokes model and Stokes model) and design domain settings. The optimized designs are shown in Fig. 3. Only a few discrete ﬁns exist in the designs for a pressure drop of 10 Pa. More pin ﬁns in streamlined shapes show up in the opti- mized designs with increase in prescribed pressure drop and in the designs for DP ¼ 200 Pa the distributions of ﬁns form complex channel networks. The change of ﬁn layouts with pressure drop shows a balance between increasing convection surface and reduc- ing ﬂow resistance in the optimized designs. The designs under a pressure drop of 10 Pa are quite similar apart from the one using Navier-Stokes ﬂow model and designable inlet and outlet setting (NSD setting). Comparison of the velocity ﬁelds of the similar designs shows that the inertia term in the Navier-Stokes equation produces slight differences mainly in the inlet and outlet regions, while the temperature ﬁelds of these designs are very similar. In contrast, the designs of different ﬂow models present different layouts under pressure drops of 50 Pa and 200 Pa. Thick branches of channels are observed close to the outlet in the Navier-Stokes designs. Inclined inlet or large and extending round corners beside the inlet are formed in the Navier-Stokes designs under a pressure drop of 200 Pa to bend the ﬂow smoothly. Optimization histories of designs under a pressure drop of 200 Pa are given in Fig. 4. The maximum temperatures follow sim- ilar trends to those of the corresponding objective functions during optimization. Each time the penalization parameter on material effective thermal conductivity is updated, the optimizations show slight oscillations at the beginning and then become stable gradu- ally. The designs in Fig. 3 are re-evaluated under pressure drops different from the design value and the cross-check results are plotted in Fig. 5. As expected, each design performs best under the pressure drop for which it is optimized, and thereby the effec- tiveness of topology optimization is justiﬁed. Table 1 Material properties and dimensions of the heat sink for topology optimization. 5.2. Model validation Parameters Water density Water viscosity Water heat capacity Water conductivity Silicon conductivity Length of heat sink Height of design layer Height of substrate Symbols q0 l C kf ks L 2Ht 2Hb 3 Values 998 1:004 10 4180 0.598 149 10 0.5 0.2 Units kg=m3 Pa s J= kg K ð Þ ð W= m K ð W= m K mm mm mm Þ Þ To validate the developed two-layer heat sink model, all the optimized designs in Fig. 3 are built as full three-dimensional heat sinks and re-evaluated using the conjugate heat transfer module in Comsol Multiphysics software. As an example, the designs optimized using the NSP setting and the corresponding three-dimensional heat sinks are shown in Fig. 6. The three- dimensional heat sinks are meshed using body-ﬁtted grids and three-dimensional physical ﬁelds are resolved. Two-dimensional slice plots of velocity and temperature ﬁelds are taken to compare

8 S. Yan et al. / International Journal of Heat and Mass Transfer 143 (2019) 118462 Fig. 3. Optimized designs under pressure drops of 10 Pa (left), 50 Pa (middle), 200 Pa(right). Speciﬁcally, (a) are designs of Navier-Stokes model and designable inlet and outlet setting (NSD setting), (b) are of Navier-Stokes model and passive inlet and outlet setting (NSP setting), (c) are of Stokes model and designable inlet and outlet setting (SD setting), (d) are of Stokes model and passive inlet and outlet setting (SP setting). (Black regions are ﬁns and white regions are channels). Fig. 4. Optimization histories of the objective function Tobj and maximum substrate temperature Tb;max of designs under a pressure drop of 200 Pa. Objectives and maximum temperatures scaled by objectives of the correpsonding initial guesses are plotted. The sub-ﬁgures (a)-(d) are for the corresponding designs in Fig. 3(a)-(d), respectively. with the two-layer model results. Fig. 7(a)-(c) show the physical ﬁelds of the designs optimized for pressure drops of 10 Pa, 50 Pa and 200 Pa respectively. The upper three sub-ﬁgures in Fig. 7(a)-(c) are respectively the velocity magnitude ﬁeld (left) and temperature ﬁeld (middle) on the mid-plane of the design layer and temperature ﬁeld on the mid-plane of the substrate (right) computed by the two-layer heat sink model. The lower sub-ﬁgures are the ﬁelds from the three-dimensional simulations.

分享到：

赞收藏

资料库

2019--Topology optimization.pdf

相关推荐

课程资源

热门标签

最新资料