logo资料库

2014年数学建模A题论文.pdf

发布时间：2022-06-18 发布人：admin 分类：说明书 资料大小：0.70M 资料格式：pdf 举报 版权申诉
第1页 / 共24页
第2页 / 共24页
第3页 / 共24页
第4页 / 共24页
第5页 / 共24页
第6页 / 共24页
第7页 / 共24页
第8页 / 共24页
资料共24页，剩余部分请下载后查看
    2014高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了《全国大学生数学建模竞赛章程》和《全国大学生数学建模竞赛参赛规则》（以下简称为“竞赛章程和参赛规则”，可从全国大学生数学建模竞赛网站下载）。我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。我们知道，抄袭别人的成果是违反竞赛章程和参赛规则的，如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。我们郑重承诺，严格遵守竞赛章程和参赛规则，以保证竞赛的公正、公平性。如有违反竞赛章程和参赛规则的行为，我们将受到严肃处理。我们授权全国大学生数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的报名参赛队号为（8位数字组成的编号）：所属学校（请填写完整的全名）：参赛队员(打印并签名)：1.2.3.指导教师或指导教师组负责人(打印并签名)：（论文纸质版与电子版中的以上信息必须一致，只是电子版中无需签名。以上内容请仔细核对，提交后将不再允许做任何修改。如填写错误，论文可能被取消评奖资格。）日期：年月日赛区评阅编号（由赛区组委会评阅前进行编号）：
    2014高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：评阅人评分备注全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：
    1嫦娥三号软着陆轨道设计与控制策略摘要本文从建立月心天球坐标系和月心惯性坐标系开始，对嫦娥三号着陆准备阶段和实现软着陆阶段的空间轨迹进行了详细的建立，继而，对软着陆中的六个过程做出了分析，在此过程中之后就引出了对其的最优控制策略。紧接着最后对建立的模型做出相应的综合分析，从而得出其误差和敏感性情况。针对问题一:首先建立将月球视为球体来建立均匀球体下的三维软着陆模型。根据建立的三个立体坐标系，月心赤道惯性系与月心惯性参考系。依据已有的着陆点经纬度海拔高度和建立的模型、方程就可以得到近月点（19.0465W,28.9987N,48km)和远月点(160.9536E,69.3124S)的具体的位置。针对近月点（1.69575km/s)远月点(1.61392km/s)的速度的问题，采用积分方程和二维的天体运动两种方法来得出并相互验证。针对问题二:嫦娥三号到达月面软着陆的轨道和在各个阶段的最优控制,在不考虑月球自转的基础上建立了月球探测器在三维空间飞行的精确动力学模型。以燃耗最优为指标,利用Pontryagin极大值原理,得到了发动机推力开关曲线和推力方向角的最优控制律综合考虑落点位置和速度约束求解两点边值问题,确定着陆轨道最优控制的燃料为1881.9kg,得到了探测器软着陆的最优轨线。针对问题三:以前两问为基础，对其进行误差分析，在嫦娥三号探月过程中除了我们已知的影响因素比如月球自转等，还存在着一些不确定因素，这里要对这些不确定的因素进行敏感性分析。建立误差模型，这里建立模型为力学模型，再将模型改为矩阵形式，做出相应的误差图形。关键字：坐标系飞行动力学建模最优控制Pontryagin极大值原理矩阵敏感性分析1.问题背景及意义1.1、问题的背景小平同志曾说过：科学技术是第一生产力。生产力的提高尤其需要高新技术来拉动。月球探测工程是一项多学科高技术集成的系统工程，实施这样的重点工程将强有力地带动信息技术、新能源技术、新材料技术、微机电技术、遥科学等其它高新技术的发展。近年来，科教兴国战略为我国培养了不少航天人才，我们对未知的事物也充满了想象和期待。在中国探月40年的历史中，终于在2004年，中国正式开展月球探测工程，并命名为“嫦娥工程”。对于嫦娥工程的进程，我们也高度重视着。2007年底嫦娥工程的第一阶段计划，是预定于2007年年底前，发射中国第一颗月球探测卫星“嫦娥一号”环绕月球运行，及进行为期一年的月球探测任务。中国探月工程二期的技术先导星“嫦娥二号”,2010年10月1日傍晚从西昌卫星发射中心成功发射升空，开始了中国绕月探月卫星的二度奔月之旅。2008年2月15日，国务院正式批准探月工程二期“嫦娥三号”立项。2013年前后，实现月面软着陆，开展就位探测和巡视探测。北京时间12月10日晚，嫦娥三号已经
    2成功降轨进入预定的月面着陆准备轨道，这是嫦娥三号“落月”前最后一次轨道调整。在实施软着陆之前，嫦娥三号还将在这条近月点高度约15公里、远月点高度约100公里的椭圆轨道上继续飞行。期间，将稳定飞行姿态，对着陆敏感器、着陆数据等再次确认，并对软着陆的起始高度、速度、时间点做最后准备。根据其环月轨道以及着陆点，我们对嫦娥三号软着陆贵高设计和控制策略问题进行研究。1.2、问题的意义月球是离地球最近的天体，成为空间探测的首选目标，月球探测将为继空间站之后载人航天的下一步人类重返月球和建立月球基地提供依据，对月球本身的科学研究可以大大提高人类对宇宙的认识。2.问题的重述月球作为地球的唯一一颗天然卫星以及太阳系第五大卫星，其神秘性以及丰富的资源一直吸引着人类，特别是近代以来地球多种资源的枯竭，以及人类文明发展对资源的需求却与日俱增。人类把目光投向了月球，但是若要对月球进行直接的科学考察并开发利用月球资源就必须解决人类航天探测器的着陆以及月夜生存等重大问题。软着路即通过减速使航天器在接触地球或其他星球表面瞬时的垂直速度降低到最小值从而实现安全着陆的技术。软着陆的目的是保证航天员的安全和航天器上的仪器设备完好无损，获得丰富的学科资料。2013年12月2日1时30分，嫦娥三号成功成功发射，12月6日抵达月球轨道，12月10日成功降轨，实现了嫦娥三号的软着路。嫦娥三号具体情况如下：着陆准备轨道上的运行质量为2.4顿，主减速发动机可产生可调节推力1500N到7500N，比冲为2940m/s，预定着陆点为19.51W，44.12N，海拔为-2641m。嫦娥三号在高速飞行的情况下实现软着陆，关键问题是着陆轨道与控制策略的设计。基本要求是着陆准备轨道为近月点15km，远月点100km的椭圆形轨道；着陆轨道为从近月点至着陆点，其软着陆过程共分为6个阶段：着陆准备轨道、主减速段、快速调整段、粗避障段、精避障段、缓速下降阶段。在上述基础上确定着陆准备轨道近月点和远月点的位置，嫦娥三号相应速度的大小与方向，着陆轨道和在6个阶段的最优控制策略，并且设计着陆轨道和控制策略做相应的误差分析和敏感性分析已获得最优解决方案。根据上述的基本要求，请你们建立数学模型解决下面的问题：（1）确定着陆准备轨道近月点和远月点的位置，以及嫦娥三号相应速度的大小与方向。（2）确定嫦娥三号的着陆轨道和在6个阶段的最优控制策略。（3）对于你们设计的着陆轨道和控制策略做相应的误差分析和敏感性分析。3.问题的分析问题一的分析：该问题中要确定“嫦娥三号”在着陆准备中近月点和远月点的位置和相对应的速度，那么我们需要明确卫星围绕月球的轨迹。在嫦娥三号着陆准备轨道中，
    3其距离月面相对较高,且嫦娥三号走过的月面距离比较长,将月球视为平面建立模型会带来较大的偏差。因此,制动段有必要将月球视为球体来建立均匀球体下的三维软着陆模型。根据建立的三个立体坐标系，可以测得一些轨道根数，然后得出月心赤道惯性系与月心惯性参考系之间的变换关系，继而月心赤道惯性系就确定了下来。接着，依照图1.3和已有的着陆点经纬度海拔高度还有matlab程序编程就可以得到近月点和远月点的其中一个具体的位置。但根据分析，该卫星的轨迹不应该是一个确定的位置，它应该是一条圆形轨迹，所以得出了图1.4。速度和方向本文建立了两个模型来计算，从而达到相互验证的效果。问题二的分析：嫦娥三号的软着陆过程可分为六个阶段，分别为主减速阶段、快速调整阶段、粗避障阶段、精避障阶段、缓速下降阶段和自由落体阶段。其中离轨段和自由下降段一般为一从100～15km的霍曼转移问题;在动力下降段制动发动机连续工作,使飞行器从距月面15km下降到3km,且使位置、速度满足一定条件;最终着陆段主要是调整飞行器姿态,使其安全着陆到月面。利用高斯-伪谱法着陆轨道参数进行研究，据分析，燃料的使用与发动机的推力大小以及飞行器的飞行时间有关，燃料的消耗主要在主减速阶段和快速调整阶段，因为在这两段过程中，发动机主要提供减速动力，因此，我们可以在该过程中合理控制嫦娥三号的速度，方向与推力大小。粗避障、精避障、以及缓速下降阶段，发动机推力方向竖直向下，此段可理解为嫦娥三号做直线运动；最后发动机关闭，此段为自由落体，不需要考虑燃料问题。问题三的分析：要求我们对对着陆轨道和控制策略做相应的误差分析和敏感性分析，我们对数据的处理以及其中忽略的问题使得我们的结论存在一定的误差，利用误差传递矩阵可以得到我们确定的着陆轨道与实际轨道之间的误差。在嫦娥三号探月过程中除了我们已知的影响因素比如月球自转等，还存在着一些不确定因素，这里要对这些不确定的因素进行敏感性分析。4.基本假设1、假设不存在摄动影响。即忽略其他天体对嫦娥三号的引力和其他因素，卫星不会偏离原来的轨道。2、假设月球探测器在一个固定的铅垂面内运动，没有考虑侧向运动。3、不考虑卫星的自身火箭推力。4、不考虑月球自转。5、月球近似一个质量均匀的标准球体。5.符号定义说明：升交点赤经i0：轨道倾角：旋转角r0：月球平均半径
    4h1:海拔高度g：重力加速度G：万有引力常量h:近月点距离月球表面的距离H：远月点距离月球表面的距离v1：近月点的速度v2：远月点的速度0L：近月点经度0L：近月点纬度'0L:远月点经度'0L：远月点纬度6.模型建立与求解6.1问题一的模型建立与求解6.1.1近月点和远月点位置模型的建立：本文涉及的坐标系均为右手坐标系，主要包括地心坐标系和月心坐标系两种类型，由于“嫦娥三号”为研究对象，本文重点介绍月心坐标系，具体如下：（1）月心天球坐标系该坐标系为惯性坐标系，其基准平面和指向均与地心天球坐标系相同，仅是原点移到了月心。该坐标主要用于地心坐标系和月心坐标系之间的平移转换，用rrrZYOX表示，坐标原点位于月心，基本平面平行于地球的J2000.0平赤道，rX指向J2000.0平春分点，rZ轴指向J2000.0平天极。该坐标系仅用于软着陆下降轨迹和制导律设计中。
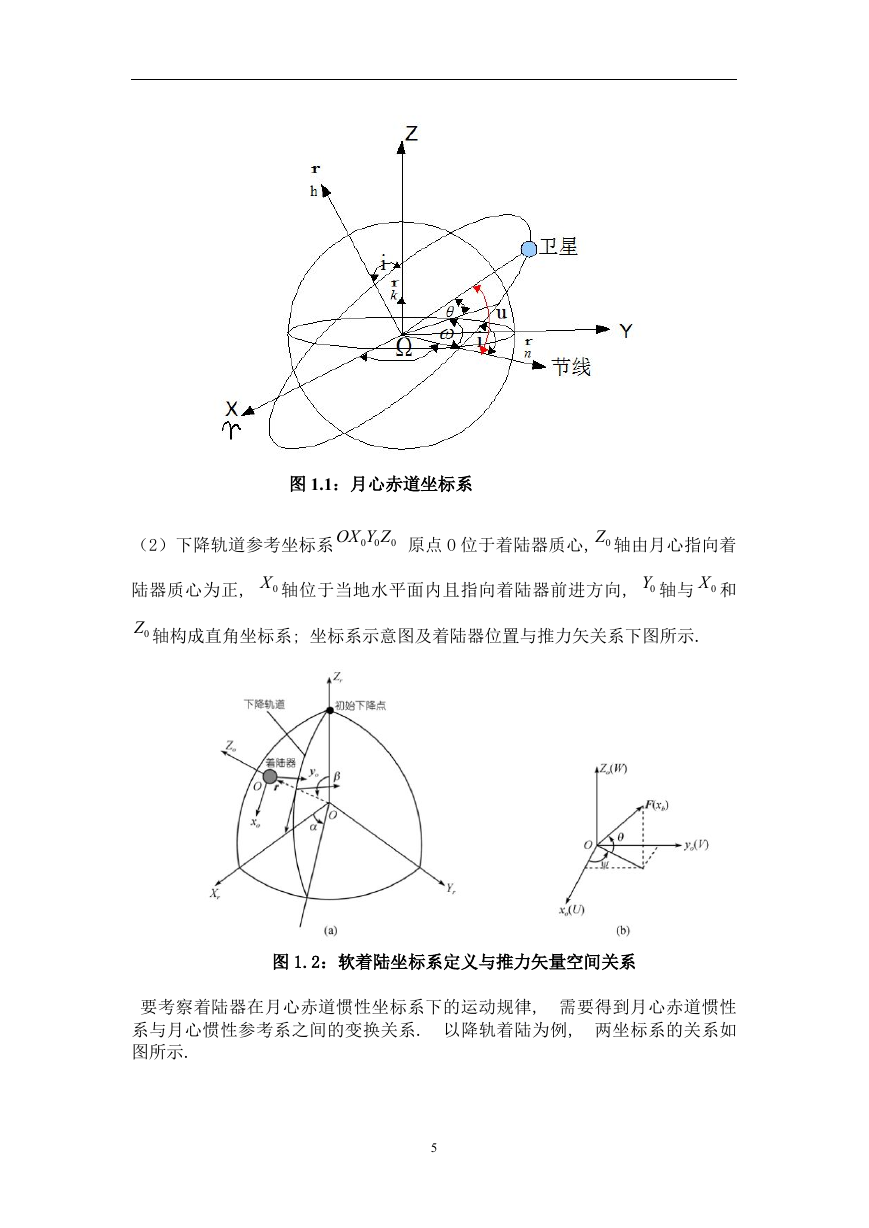
    5图1.1：月心赤道坐标系（2）下降轨道参考坐标系000ZYOX原点O位于着陆器质心,0Z轴由月心指向着陆器质心为正,0X轴位于当地水平面内且指向着陆器前进方向,0Y轴与0X和0Z轴构成直角坐标系;坐标系示意图及着陆器位置与推力矢关系下图所示.图1.2：软着陆坐标系定义与推力矢量空间关系要考察着陆器在月心赤道惯性坐标系下的运动规律,需要得到月心赤道惯性系与月心惯性参考系之间的变换关系.以降轨着陆为例,两坐标系的关系如图所示.
    6图1.3：月心赤道惯性系与月心惯性参考系之关系可以看出,由月心赤道惯性系OXYZ变换到月心惯性参考系ZYXrrrO需经过4次旋转：。。901800XZXZi由此可以得出他们之间的坐标变换矩阵CrI为：。。180900CiCCCCZXZXrI其中，i0为环月停泊轨道的轨道倾角，软着陆下降轨道位于环月轨道平面内；为环月停泊轨道的升交点赤经，旋转角可利用上图中（b）中的球面三角形'LMN求得，其中L为着陆点位置，'N为环月轨道降交点，01sinsinsin--90--90i。。该式中，为着陆点赤经，事先给定；为嫦娥三号经过的月心角，可通过仿真得出。于是月心赤道惯性系下的位置可表示为：TrrrTrITZYXC,,ZY,X,其中，月心惯性参考系下的位置表示由图1.2中给出，如下：
    分享到：
    赞 收藏

    相关推荐

    资料库

    信息化

    共收录1827份资料，累计6个分类，关注成员有19位，主要包括：管理软件,企业管理,电子商务,其它,IT管理,项目管理

    热门标签

    管理软件 企业管理 电子商务 其它 IT管理 项目管理

    最新资料