针对中国股市的基于 CVaR 方法的投资组合模型 http://www.paper.edu.cn 严定琪 1，薛江 1，李俊娴 2 1 兰州大学数学与统计学院，兰州（730000） 2 西北大学管理学院，西安（710000） E-mail: xuej1112@163.com 摘 要：为了克服现有证券投资组合模型的不足,本文基于新近提出的风险度量方法 CVaR， 并同时兼顾多种市场摩擦因素，建立了一种新型的投资组合模型。结合中国证券市场数据的 实证测试表明，新模型不仅能合理反映不同投资约束对最优投资决策的影响，而且可帮助投 资者寻求稳健的最佳投资方案；与基于绝对偏差的 MAD 模型相比，新模型亦具有更良好的 特性。 关键词：投资组合选择模型，CVaR，市场摩擦，MAD 中图分类号：O29 1.概述 证券投资者都希望在一定的可接受的风险条件下选择利润最高的投资组合。投资证券的 价格下降，利率下调，汇率波动和债券发行者的信誉丧失等都会带来损失。对多种有价证券 进行投资可以减少特殊的风险。 在现在的研究和实际应用中，风险度量的方法也是多种多样的，它们各自的侧重点不同， 但是都有着自己独特的作用[1]。一般有期望效用模型、均值-方差模型、Var 和 CVar 方法等。 这里主要介绍 CVaR 方法。 Riskmetrics 在 1996 年给出的 VaR 的定义[2]，尽管 VaR 在关于投资组合的组成选择上在 风险的度量方面经常应用，但由于后尾问题、缺乏次可加性、解缺乏有效性等，它在数学上 去不是最好的应用模型。所以在本文中我们采用弥补了 VaR 方法缺陷的 CVaR 方法。 CVaR，是指在一定的置信水平下损失超过 VaR 的条件均值。如 Rockafellar 和 Uryasev 在 2000 年定义的[3]，在连续分布下： E R x r R x r ( , ) [ % CVaR x ( , ( , ) | ) α = % ≤ VaR x ( , )] α Nikolas Topaloglou，Hercules Vladimirou and Stavros A. Zenios（2002）[4]指出投资组合 收益的最优 CVaR 风险度量的混合整数规划问题可以表示为： max . .s t S z + s − p y s ， 1 − ∑ α s x X z R z ∈ ， Tx r μ≥% ∈ ， z R x y y ( , )] max[0, （*） − 1 , + = s y 1 = s + ≥ − s x r T s ， sy + ≥ ， 1,2, = L 0 S s , 在不同的投资组合的预期收益μ下对参数优化问题（*）的解就是 CVaR 的有效值。 CVaR x α 。而自由变量 z 的最优解是 VaR x α 的值。这个结果应经被 Rockafellar 和 Uryasev 严格的证明过了（2002， ( , ) ) 对每个整数期望收益μ，（*）的最优解是相应的 相应的 ( , Theorem 14 and Corollary 15）[3]。 2.新模型建立 在实际的投资组合中，我们要考虑到其他因素的影响，比如：投资金额、交易费用、税 收、买空卖空等的影响。因此我们对（*）进行相应的修正。假设市场上有 n 种风险资产， 在投资初期,投资者将按一定预算在这 n 种风险资产中对投资金额进行调整分配,使得期末的 - 1 - 

http://www.paper.edu.cn x x 1= ( , x 为 我 们 寻 找 的 最 优 投 资 组 合 头 寸 ， 为投资者期初所持有的投资组合头寸， 0v 为投资者初期投资的总金额， 2 ,..., nx T ) 收 益 尽 可 能 的 大 ， 设 x q x ( , 0 = 0 1 qq ( , 1= x T ) T nx ,..., 0 0 2 nq y ,..., ) 为期初各证券的市场价格， xq v T= 0 2 为在持有期期末投资证 为持有期初所拥有的资金量。进行投资优化后， 0x 调整为 x ，这 券的价格，则 期间会第一次产生手续费和税收，记为 1t 。最后只有将股票卖出才会获得收益，所以存在交 割问题，既要考虑手续费和税收，则先记为 2t 。 2 0 = ( y 1 , y ,..., ny T ) 下面考虑实际投资活动中，对投资决策有直接影响的各种市场摩擦因素和投资约束。 1.交易成本 在实际操作中，设 iu ， iv 分别为投资者在对其持有的投资组合进行调整时买入和卖出 第 i 种证券的数量。故有： x i − x 0 i = u i v + i 考虑 1t ，本文将股票买卖中存在的过户费、交易费和印花税统一考虑为比例交易成本， = ∑ 。 − 对于 2t ，则有： 2 t v i 用 k 来表示。则 1t 为： 1t = kq x i ky x i i ∑ x 0 i x 0 i u i x i − − = , n n i i 1 = i 1 = 可见总交易成本随着买卖交易量的增加而增加，不可忽略。 2. 对预期价格 y 的估计 本文通过建立GARCH(1,1)模型来预测各支股票的预期价格。通过模拟计算得到各个参 数的值，进而得到预期价格y（以下同）。 3.资本预算约束 调 整 后 的 总 投 资 额 应 不 超 过 初 始 投 资 额 ， 因 此 有 ： q x t T 1 + ≤ 0 q x T 即 ： q x T + n ∑ i 1 = kq u ( i i + v i ) ≤ 0 q x T 4.最小收益率约束 当考虑税收和交易费用时，期末预期净收益函数 ,(~ yxR ) 则在最小收益率为μ下，将 1t ， 2t 代入,可得到约束条件 R(x,y)。 5.证券投资头寸约束 实际操作中，要求对某一单个证券的投资头寸不超过一定的范围，设 x x 分别为对第 ,i i 个证券投资的上下限。 iu ， iv 分别为 iu iv 的上界。 ib 表示对第 i 个证券所允许的最大投资 比例。 i 根据上述分析，可以得到修正后的新模型如下： s yp + s 1 − max 1 ∑ = S z s − α 1 zXx , ℜ∈ ∈ s.t. n ∑ ∑ y x i i = − ) n i 1 = i 1 = R x y ( , n ∑ i 1 = kq u ( i i + v i ) − ky x i i − 0 q x T (1 + k ) ≥ [ μ n ∑ i 1 = q x i i + n ∑ i 1 = k q u ( i i i + v i )] （存在税收和交易费用下的最小收益率约束） q x T q x T k q u ( i i v i + + ≤ ) n 0 i （资本约束） ∑ i 1 = - 2 - 

n ∑ i 1 = n i ( xy si i − xq i 0 i ,) y + s ≥ ,0 s = ,2,1 ,..., S （单个证券投资头寸约束） http://www.paper.edu.cn y + s −≥ z q x i i ≤0 q x i i ≤ ∑ （单个证券投资比例约束） b i u ≤ i v − 利用以上对 CVaR 新模型的描述中的假设，我们根据在 Konno 和 Yamazaki（1991）[5] v v ≤ （单个证券投资头寸变化约束） i i u v ,0 ≥ 1 = ≤0 ， x 0 i ≤ ， ix 为正整数，i=1,2,…,n。 x i x ， i x i u i x i ≥ 0 = i ， i − ≤ i u i 的 MAD 框架建立相关的 MAD 模型并进行数据对比。 3.数据对比测试 我们建立的 CVaR 模型可以方便的用于大规模的投资组合问题，所以我们从深圳和上海 证券市场选取了 100 只股票，用它们从 2006 年 1 月 4 日到 2006 年 12 月 19 日的每个交易日 的收盘价格作为原始的数据，这样每只股票有历史数据 220 个。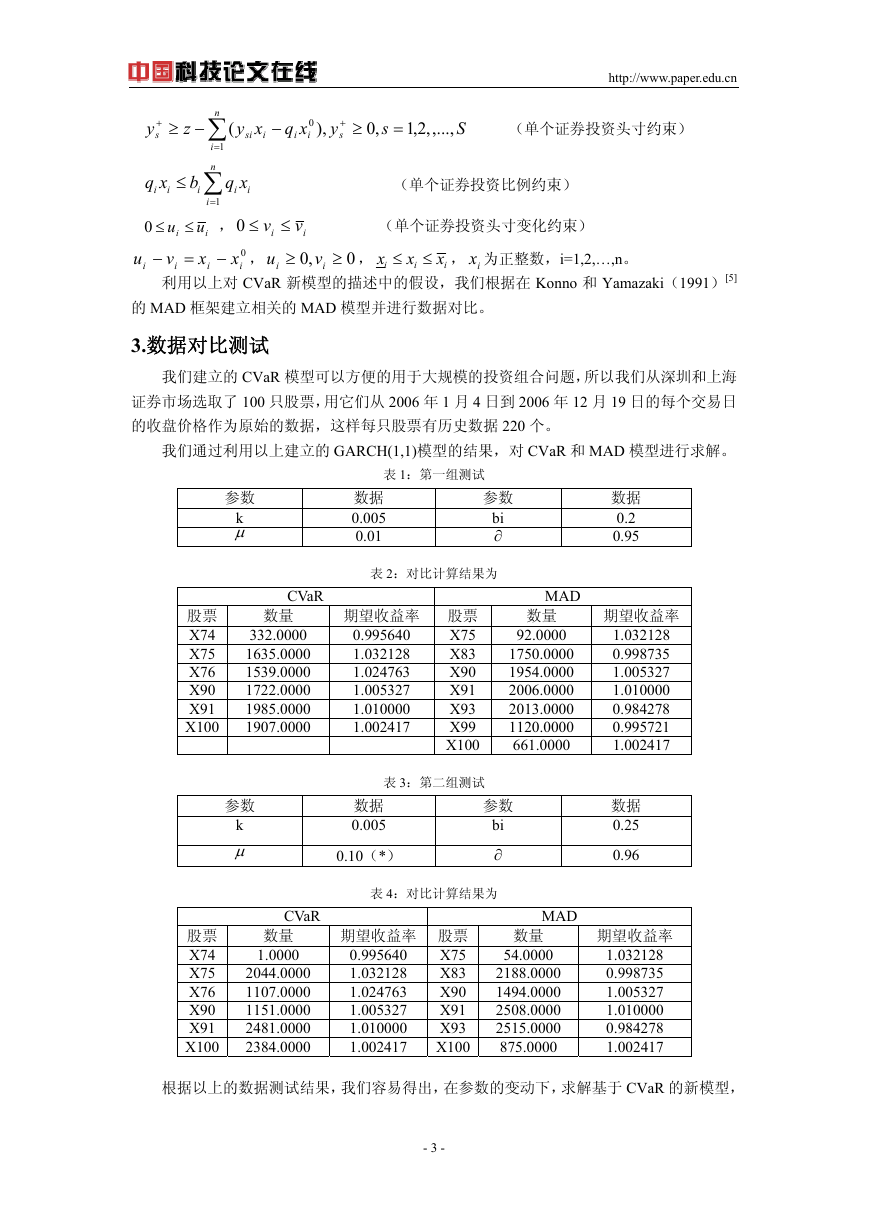 我们通过利用以上建立的 GARCH(1,1)模型的结果，对 CVaR 和 MAD 模型进行求解。 参数 k μ 表 1：第一组测试 数据 0.005 0.01 参数 bi ∂ 表 2：对比计算结果为 数据 0.2 0.95 股票 X74 X75 X76 X90 X91 X100 CVaR 数量 332.0000 1635.0000 1539.0000 1722.0000 1985.0000 1907.0000 期望收益率 股票 0.995640 X75 X83 1.032128 X90 1.024763 1.005327 X91 X93 1.010000 X99 1.002417 X100 MAD 数量 92.0000 1750.0000 1954.0000 2006.0000 2013.0000 1120.0000 661.0000 期望收益率 1.032128 0.998735 1.005327 1.010000 0.984278 0.995721 1.002417 参数 k μ 表 3：第二组测试 数据 0.005 0.10（*） 参数 bi ∂ 表 4：对比计算结果为 数据 0.25 0.96 股票 X74 X75 X76 X90 X91 X100 CVaR 数量 1.0000 2044.0000 1107.0000 1151.0000 2481.0000 2384.0000 期望收益率 股票 X75 0.995640 X83 1.032128 1.024763 X90 X91 1.005327 1.010000 X93 X100 1.002417 MAD 数量 54.0000 2188.0000 1494.0000 2508.0000 2515.0000 875.0000 期望收益率 1.032128 0.998735 1.005327 1.010000 0.984278 1.002417 根据以上的数据测试结果，我们容易得出，在参数的变动下，求解基于 CVaR 的新模型， - 3 - 

http://www.paper.edu.cn 其结果所选出的股票的期望收益率大部分都是大于 1 的，也就是说，这些股票的期望期末价 格都大于初始价格。另外，近年来中国股市一直处于低迷状态，所以，这些被选出的股票都 是绩优股，即具有很强的抗风险性和很高的收益率，适合于投资者选择作为下一步的投资组 合方案。同时，我们可以看出，新模型比 MAD 模型表现出了更高的收益增长和更低的风险 性，表明新模型比 MAD 模型具有更良好的特性。 参考文献 [1]. 田新民,黄海平. 基于条件VaR(CVaR) 的投资组合优化模型及比较研究. 数学的实践与认识，2004年, 第34卷,第7期 [2].Riskmetrics. Technical document, 4th edition. J.P. Morgan Inc., December 1996. [3].Rockafellar R.T., Uryasev S.. Conditional value-at-risk for general distributions. Journal of Banking and Finance, 2002,26(7). [4]. Nikolas Topaloglou，Hercules Vladimirou and Stavros A. Zenios. CVaR models with selective hedging for ternational asset allocation. Journal of Banking & Finance，2002,P1534-1565. [5].Konno H., Yamazaki H.. Mean absolute deviation portfolio optimization model and its application to Tokyo stock market. Management Science, 1991,37(5)519–531. Portfolio Selection Model of Chinese Stock Market Base on Risk Measure CVaR Yan Dingqi1,Xue Jiang1,Li Junxian2 1 Department of Mathematics and statistics,LAN Zhou University,LAN Zhou (730000) 2 Department of public management, Northwest University,Xi’an (710000) Abstract To overcome shortcomings of existing portfolio selection models, established in this paper is a new model which utilizes the recently introduced risk measure CVaR and takes into consideration several market frictions simultaneously. Basing trading data from the China Stock Market, empirical results show that the proposed new model can not only properly reflect the effect of different investment constraints on the optimal investment decision, but be helpful for investors to find robust optimal portfolio. The new portfolio selection model also has superior properties when compared with the corresponding portfolio selection model basing on the absolute deviation. Keywords: portfolio selection model,CVaR, market frictions,MAD 作者简介： 严定琪 男，兰州大学 数学与统计学院副教授，研究方向，证券投资。 薛江（1982-），男，陕西西安人，兰州大学 数学与统计学院研究生，研究方向，证券投资。 李俊娴（1983-），女，陕西西安人，西北大学公共管理学院硕士研究生，研究方向社保基金 管理。 - 4 -