中国科技论文在线 http://www.paper.edu.cn 基于 SIFT 算法的影像匹配精度评价研究 杨健* （中国矿业大学环境与测绘学院，江苏 徐州 221116） 摘要：SIFT 算法是目前影像匹配领域的研究热点之一。该算法的主要思想是：在尺度空间 中寻找极值点，提取位置、尺度、旋转不变量，这不同于一般的基于灰度的匹配算法，因此 SIFT 算法的通用性很强。本文在实现 SIFT 算法进行影像匹配的基础之上，利用在影像上的 特定区域可以进行灰度模板匹配的情况，对 SIFT 算法的定位精度进行分析，提出了一种评 价 SIFT 算法定位精度的可行方案。 关键词：摄影测量与遥感；SIFT 算法；影像匹配；灰度模板；精度评价 The research of accuracy estimation of SIFT algorithm for the image matching Yang Jian JiangSu XuZhou 221116) (Environmental and Spatial information School, China University of Mining and Technology, Abstract: The algorithm of SIT is one of the hot research point in the area of image matching recently. The main thinking of this algorithm is: find the extreme point in the scale area, extract the invariant with the location and scale, circum; this is different from the image matching method that bases the degree of the darkness panel; so the currency of SIFT algorithm is powerful. This paper advances a feasible method to estimate the accuracy of SIFT algorithm bases the case that some area in the image can be matched by the traditional darkness image matching method. Meanwhile, we also realize the SIFT algorithm. Keywords:Photogrammetry and Remote Sensing;SIFT algorithm;Image matching;the darkness panel; accuracy estimation 0 引言 目前主流的影像匹配算法大致可以分成两种类型：第一类是在以待定点为中心的窗口 （或称区域）内，以影像的灰度分布为影像匹配的基础，故称此种类型的算法为灰度匹配 （Area Based Image Matching）；第二类是基于影像特征的匹配，主要用于配准特征点、线 或面，这一类算法称为特征匹配（Feature Based Matching）[1-2]。SIFT（The Scale Invariant Feature Transform）算法，全名是尺度不变特征转换算法。SIFT 特征匹配算法属于基于特征 的匹配算法中的一种。SIFT 算法在特征提取、特征描述和特征匹配这三个方面都有自己独 特的特点，因此 SIFT 算法是目前影像匹配领域的研究热点之一。 本文在实现 SIFT 算法进行影像匹配的基础之上，对 SIFT 算法的定位精度进行分析， 提出了一种评价 SIFT 算法定位精度的可行方案。 1 基于 SIFT 算法的影像匹配 SIFT 特征匹配算法最初由加拿大的英属哥伦比亚大学（British Columbia）的 David G. Lowe 教授提出。该教授在 1999 年 9 月召开的计算机视觉国际会议（International Conference on Computer Vision）上发表了名为《Object Recognition from Local Scale-Invariant Features》 的一篇论文。在该论文里，作者第一次提出了尺度不变特征的概念，并将其应用于影像匹配 作者简介：杨健（1987-），男，硕士研究生，主要研究方向是：摄影测量与遥感. E-mail: yangjiancumt@126.com - 1 - 

中国科技论文在线 http://www.paper.edu.cn 领域。2004 年 1 月，该教授发表了名为《Distinctive Image Features from Scale-Invariant Keypoints》的文章，在原来提出的算法的基础之上进行了一定的改进工作，这些改进主要 包括 SIFT 特征点的精确定位和特征点描述子的改进等工作，从而使 SIFT 算法得到完善[3]。 使用 SIFT 算法进行影像匹配，大体上可以分为四个步骤。 1.1 在多尺度空间上生成高斯影像和高斯差分影像 在不同的尺度空间上生成高斯影像和高斯差分影像是进行 SIFT 特征点检测的第一步， 也 是 SIFT 特 征 点 检 测 算 法 的 一 个 重 要 特 点 。 生 成 高 斯 影 像 使 用 的 函 数 为 ： yxG ,( ) , σ = 1 2 2 πσ 2 + y 2 2/) 2 σ xe ( − ，实际操作中我们使用这个函数生成一个高斯平滑掩膜，然 后使用这个掩膜对影像进行处理。 按照逐步平滑处理的方法，一共可以生成 3 组高斯影像。在 3 组高斯影像的基础之上， 进行差分运算，又可以得到 3 组高斯差分影像。 1.2 进行极值检测、极值点精确定位和去除低对比度点、边缘响应点 由于 SIFT 算法的原理较为模式化，相关文献以给出详细描述，本文不再赘述。值得注 意的是，极值点的检测工作在同尺度的高斯差分金字塔影像之间进行，检测工作发生在相邻 的连续三张影像之间。检测的结果显示在中间一层影像上。据此可知，每组高斯差分影像上， 特征点的检测的结果显示在第二层和第三层之间。在这两层影像上，分别进行特征点的搜索 工作，但是对每层搜索影像而言，又有相邻的两层影像参与其中。这样做的目的是确保在尺 度空间和二维图像空间都检测到极值点。 1.3 为特征点分配方向和 SIFT 特征点描述子的生成 分配方向的目的就是：利用关键点邻域像素的梯度方向分布特性为每个特征点指定方向 参数，使算子具备旋转不变性。该步骤主要利用关键点相邻区域内一定像素的梯度值和模来 完成主方向的分配工作。 以 SIFT 特征点为中心取一个 16×16 的一个窗口，在每 4×4 的小块上计算 8 个方向的 梯度方向直方图，绘制每个梯度方向的累加值，即可形成一个 128 维的向量，将这个向量作 为 SIFT 特征点的描述子。 1.4 使用特征向量进行影像匹配工作 当两幅图像的 SIFT 特征向量生成后，采用特征点特征向量之间的欧式距离作为两幅图 像之间特征点的相似性判定度量。 向量之间的欧式计算类似于两点之间进行距离运算，也就是将向量中的相应的元素两两 与 B 图像中的所 求差后再进行平方和运算。算例如下：A 图像中的向量 ) , na a , 2 进行欧式距离的计算： aa , 1 = ( 有的向量 b = bi 2 , , bi n ), i = ,2,1 , N , bi ( 1 bi 1 − − + = ( + ( 2 ) 2 ) a 1 a 2 bi 2 L 求出最小的距离 minL 和次小的距离 cminL,然后计算两个距离的比值 minL/cminL，如 果该比值小于 0.8 就接受这一对匹配点。否则舍弃该点进行下一个特征点的计算工作。在操 作过程中应该使用 KDTree 数据结构进行运算。 ,2,1 2 ,) a n bi N , = − + ( i n - 2 - 

中国科技论文在线 2 匹配点评价的基本方法与匹配精确定位方法 http://www.paper.edu.cn 匹配点评价的基本方法有若干种，本文选择使用在粗匹配的基础之上进行精确匹配来确 定匹配点的精度的方法。 2.1 匹配点评价的基本方法 目前评价点位的精度主要从三个方面入手： （1）SIFT 算法的模型精度。在原文的文献中，作者只是介绍其精度可以达到亚像素级， 但是并没有说明具体是多少，因为精度不仅与模型有关系，也和进行匹配的图像的特点（如： 噪声大小，视角等）有关系。查阅目前几乎所有的文献，基本没有从 SIFT 模型出发去评价 该算法的精度的文章，也没有找到相关的关于 SIFT 模型的精度。 （2）利用匹配出的点位计算物方坐标值，然后与该点的真实值相比较，从而得到该点 位的物方精度。这是最常用的一种方法，但是该方法需要一定的控制点参与，限制其在实验 室条件下的应用。 （3）计算匹配点的精确值与 SIFT 匹配出的点位相比较，从而得到 SIFT 匹配点的偏差 值。这就带来一个问题：如何计算出匹配点的精确位置，如果目标是一个角点或圆形标志点， 可以使用已有的定位算子来完成精确定位工作。但是，遥感影像上都是无规则形状的特征点， 因此可以考虑使用二次多项式拟合的方法来求得该特征点的精确位置。 2.2 在初始位置基础上的影像精匹配 在得到的 SIFT 特征点的像素级坐标的基础之上，在左右片上做如下处理：左片上，以 该像素为中心取 3╳3 的模板邻域；右片以相应的像素为中心取 5╳5 的搜索区域。在搜索区 域内，采用模板区域计算相关像素的相关系数，计算公式如下： n m ∑∑ = 1 j 1 = i n m ∑∑ 1 = j 1 = C = i 其中： [ yxf , ( i i ) − yxgf , ][ i ( i ) − g ] [ yxf , ( i i ) − f 2 ] yxg ([ , i i ) − g ] 2 n m ∑∑ i 1 = j 1 = f = 1 × NM ∑ i , j yxf ( , i j ,) g = 1 × NM ∑ i , j yxg , ( i j ) 这样就可以在右片上得到匹配点周围的 9 个点的相关系数值，通过这 9 个点可以采用最 小二乘法拟合出一个二元二次曲面方程： ex + cxy bx + + + 2 2 f ) = + ay dy yxP ,( 利用 Matlab 数学软件采用最小二乘法可以得到上式的各个系数[4]： >> X=[-1 0 1 -1 0 1 -1 0 1]'; >> Y=[-1 -1 -1 0 0 0 1 1 1]'; >> Z=[C1 C2 C3 C4 C5 C6 C7 C8 C9]'; >> Q=[ones(size(X)) X Y X.^2 Y.^2 X.*Y]; >> a=inv(Q'*Q)*Q'*Z 这样依次可以得到：f e d b a c 的值。 - 3 - 

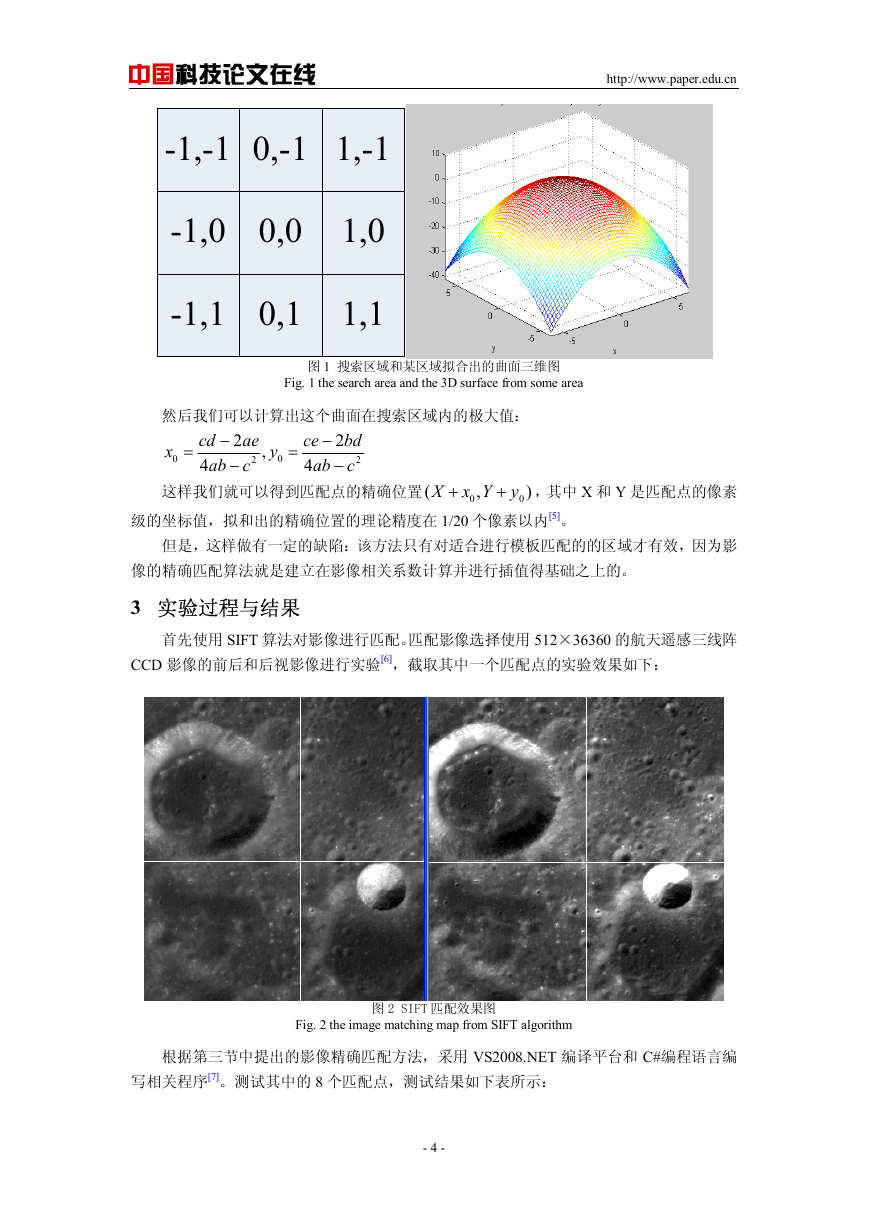
中国科技论文在线 http://www.paper.edu.cn -1,-1 0,-1 1,-1 -1,0 0,0 -1,1 0,1 1,0 1,1 图 1 搜索区域和某区域拟合出的曲面三维图 Fig. 1 the search area and the 3D surface from some area 然后我们可以计算出这个曲面在搜索区域内的极大值： x 0 = cd − ab 4 2 − ae c 2 , y 0 = ce − ab 4 bd 2 c 2 − 这样我们就可以得到匹配点的精确位置 ( yYxX + + , 0 ) 0 ，其中 X 和 Y 是匹配点的像素 级的坐标值，拟和出的精确位置的理论精度在 1/20 个像素以内[5]。 但是，这样做有一定的缺陷：该方法只有对适合进行模板匹配的的区域才有效，因为影 像的精确匹配算法就是建立在影像相关系数计算并进行插值得基础之上的。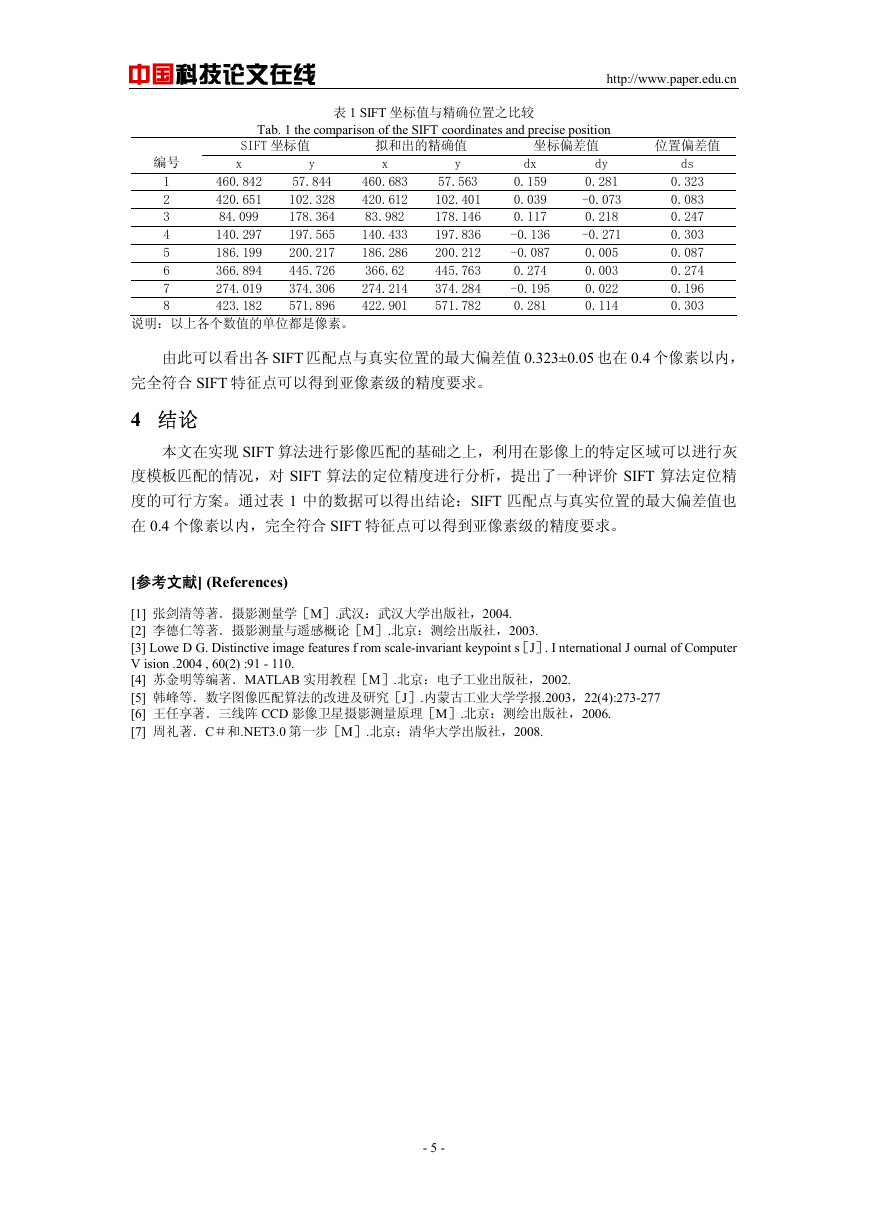 3 实验过程与结果 首先使用 SIFT 算法对影像进行匹配。匹配影像选择使用 512×36360 的航天遥感三线阵 CCD 影像的前后和后视影像进行实验[6]，截取其中一个匹配点的实验效果如下： 图 2 SIFT 匹配效果图 Fig. 2 the image matching map from SIFT algorithm 根据第三节中提出的影像精确匹配方法，采用 VS2008.NET 编译平台和 C#编程语言编 写相关程序[7]。测试其中的 8 个匹配点，测试结果如下表所示： - 4 - 

中国科技论文在线 http://www.paper.edu.cn 表 1 SIFT 坐标值与精确位置之比较 Tab. 1 the comparison of the SIFT coordinates and precise position 坐标偏差值 编号 1 2 3 4 5 6 7 8 SIFT 坐标值 x y 拟和出的精确值 x y 460.842 420.651 84.099 140.297 186.199 366.894 274.019 423.182 57.844 102.328 178.364 197.565 200.217 445.726 374.306 571.896 460.683 420.612 83.982 140.433 186.286 366.62 274.214 422.901 57.563 102.401 178.146 197.836 200.212 445.763 374.284 571.782 dx 0.159 0.039 0.117 -0.136 -0.087 0.274 -0.195 0.281 dy 0.281 -0.073 0.218 -0.271 0.005 0.003 0.022 0.114 位置偏差值 ds 0.323 0.083 0.247 0.303 0.087 0.274 0.196 0.303 说明：以上各个数值的单位都是像素。 由此可以看出各 SIFT 匹配点与真实位置的最大偏差值 0.323±0.05 也在 0.4 个像素以内， 完全符合 SIFT 特征点可以得到亚像素级的精度要求。 4 结论 本文在实现 SIFT 算法进行影像匹配的基础之上，利用在影像上的特定区域可以进行灰 度模板匹配的情况，对 SIFT 算法的定位精度进行分析，提出了一种评价 SIFT 算法定位精 度的可行方案。通过表 1 中的数据可以得出结论：SIFT 匹配点与真实位置的最大偏差值也 在 0.4 个像素以内，完全符合 SIFT 特征点可以得到亚像素级的精度要求。 [参考文献] (References) [1] 张剑清等著．摄影测量学［M］.武汉：武汉大学出版社，2004. [2] 李德仁等著．摄影测量与遥感概论［M］.北京：测绘出版社，2003. [3] Lowe D G. Distinctive image features f rom scale-invariant keypoint s［J］. I nternational J ournal of Computer V ision .2004 , 60(2) :91 - 110. [4] 苏金明等编著．MATLAB 实用教程［M］.北京：电子工业出版社，2002. [5] 韩峰等．数字图像匹配算法的改进及研究［J］.内蒙古工业大学学报.2003，22(4):273-277 [6] 王任享著．三线阵 CCD 影像卫星摄影测量原理［M］.北京：测绘出版社，2006. [7] 周礼著．C＃和.NET3.0 第一步［M］.北京：清华大学出版社，2008. - 5 -