logo资料库

参数自适应的可变类FLICM灰度图像分割算法.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.37M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    第 32 卷 第 2 期 2017 年 2月 控 制 与 决 策 Control and Decision Vol.32 No.2 Feb. 2017 文章编号: 1001-0920(2017)02-0262-07 DOI: 10.13195/j.kzyjc.2016.0050 参数自适应的可变类 FLICM 灰度图像分割算法 赵雪梅, 李 玉y, 赵泉华 (辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000) 摘 要: 为解决传统 FLICM 算法需人为给定图像聚类数的问题, 基于该算法通过聚类中心描述聚类的特点, 设计 以聚类中心为操作对象的分裂合并操作, 以实现可变类图像分割. 在此基础上定义分裂合并操作的接受率, 不但 能够有效避免算法陷入局部极值, 促进其快速收敛, 同时有利于参数阈值的自适应. 分别利用所提出算法和传统 ISODATA 算法分割模拟图像和灰度纹理图像, 对其结果的定性定量分析验证了所提出算法的有效性和普适性. 关键词: 图像分割；模糊聚类；FLICM 算法；参数自适应；可变类分割 中图分类号: TP791 文献标志码: A Self-adaptive FLICM algorithm for gray image segmentation with unknown number of clusters ZHAO Xue-mei, LI Yuy, ZHAO Quan-hua (School of Geomatics，Liaoning Technical University，Fuxin 123000，China) Abstract: To determine the number of clusters in the traditional FLICM algorithm, this paper designs splitting-merging operations based on the characteristics of the FLICM algorithm which uses the mean of pixels to describe the cluster. Then, an acceptance probability is designed to promote the convergence of the algorithm, which can prevent it from being trapped into local extremes and realize the self-adaptiveness of the thresholds, simultaneously. Qualitative and quantitative analysis on the experimental results from a series of synthetic and gray texture image segmentation demonstrates the adaptability and accuracy of the proposed approach compared with the traditional iterative self organizing data analysis techniques algorithm (ISODATA). Keywords: image segmentation；fuzzy clustering；fuzzy local information C-means；self-adaptive of parameters； segmentation with unknown number of clusters 0 引 图像分割[1-2] 是图像处理的基础, 其分割结果直 接影响后续解译精度,因此图像分割一直都是图像处 理领域研究的热点问题.图像在其特征空间中自然聚 类, 基于该特性的聚类算法备受关注, 模糊 C 均值算 法是其中最为常用的算法之一. 该算法原理简单, 运 行速度快, 但对噪声和异常值敏感. 因此, 自Bezdek[3] 提出以来, 众多研究者致力于改进该算法. Krinidis 等[4] 通过定义中心像素与邻域像素隶属度间的制约 关系, 提出 FLICM(fuzzy local information C-means) 算法,有效解决了传统模糊聚类算法对噪声和异常值 敏感的问题, 但是该算法需要预先给定聚类数, 无法 实现可变类图像分割. 常发亮等[5] 采用可变码长遗传算法, 通过自适应 码长实现图像聚类数的自动确定.该方法需要重复计 算每个个体的适应度,极大程度地增加了算法的计算 量. 朱付平等[6] 首先实现了图像的过分割, 然后根据 区域间的统计特性相似度合并同质区域,最终得到理 想聚类数下的分割结果.该方法利用平滑后的图像进 行分割, 会导致图像细节信息的丢失, 且其对聚类数 的估计依赖于过分割的精度. 向日华等[7] 利用高斯混 合模型在特征空间上制定最小法向角度差门限,通过 直接合并成份确定最终聚类数,但是基于合并的方法 对初始过分割要求较高,需要保证初始分割结果的每 个区域中只包含一个地物类别. 此外, 区域合并条件 阈值需人为给定,且基于经验阈值易导致分割结果不 收稿日期: 2016-01-11；修回日期: 2016-05-06. 基金项目: 国家自然科学基金项目(41271435, 41301479)；辽宁省自然科学基金项目(2015020190). 作者简介: 赵雪梅 (1989), 女, 博士生, 从事模糊数学的研究；李玉 (1963), 男, 教授, 博士生导师, 从事遥感数据处 理等研究. 通讯作者. E-mail：liyu@lntu.edu.cn y
    赵雪梅 等: 参数自适应的可变类 FLICM 灰度图像分割算法 第2期 稳定. ISODATA(iterative self organizing data analysis techniques algorithm)[8-11] 通过相关参数与阈值的比 较判定聚类是否需要分裂合并,不再依赖于初始过分 割结果. 因此, 目前该方法在可变类图像分割中应用 较为广泛[12-14]. 但是, 其分裂合并准则的定义引入了 大量需人为给定的参数阈值,而不同影像对应不同最 优参数组合,通过反复实验的方式很难确定待分割影 像的最优聚类数. 此外, 其分裂合并操作结果未必优 于操作前, 导致算法运行时间较长, 且无法准确收敛 于最优聚类数. 直接将上述聚类数估计算法应用于FLICM 算法 无法获取准确结果, 因此本文以FLICM 算法为基础, 根据其以聚类中心描述算法聚类性质的特点设计基 于聚类空间的分裂合并操作, 以实现可变类图像分 割. 首先, 根据聚类内像素点距其聚类中心的平均距 离、聚类内方差和聚类内像素数定义聚类分裂操作; 然后, 判断两个聚类中心是否过于接近, 进而设计聚 类合并操作. 在此基础上, 定义分裂合并操作的接受 率, 该接受率不但能够避免算法陷入局部极值, 还能 使算法逐渐趋于最优. 假定算法趋于最优时, 相关参 数同样趋于最优, 在接受分裂、合并操作的前提下, 将 该分割结果的相关变量赋予对应的参数阈值,以实现 参数自适应. 最终通过不断分裂合并聚类中心, 使算 法逐渐趋于最优,并自适应地得到最优聚类数和相应 的分割结果. 1 算法描述 1.1 FLICM算法 假设 X = fxiji = 1; 2;g 表示一幅待分割 灰度图像. 其中: xi 为第 i 个像素的强度, i 为像素索 引, N 为总像素数. FLICM算法[4] 的目标函数定义为 ∥xi vj∥2 + Gij]: [um ij (1) N∑ c∑ Jm = i=1 j=1 其中: j 为类别索引; c 为当前聚类数; uij 为模糊隶 属度函数, 表示第 i 个像素隶属于第 j 个类别的程 度; m 为算法的模糊程度; vj 为第 j 个聚类的聚类中 心;jj xi vjjj2 为第 i 个像素与第 j 个聚类中心的欧 几里得距离; Gij 为模糊因子,可定义为 ∑ 1 (1 ui′j)mjjxi′ vjjj2; (2) Gij = i′2Ni;i′̸=i dii′ + 1 为邻域像素索引, dii′ 的空间距离. 最小化目标函数, 可得到模糊隶 Ni 为像素 i 的邻域像素集合, i 为 i 与 i 属度矩阵计算公式[4] 为 ′ ′ uij = ) 1 m1 : 1 ( ∥xi vj∥2 + Gij c∑ ∥xi vk∥2 + Gik / N∑ N∑ k=1 vj = (uij)mxi (uij)m: 聚类中心的计算公式如下: 263 (3) (4) i=1 i=1 最终, FLICM 算法通过迭代计算聚类中心、模糊因子 和隶属度矩阵实现给定聚类数下的图像分割. 1.2 聚类分裂合并 为了提高算法的运算速度,在判断分裂合并条件 前设置直接删除聚类和生成新聚类这两个对偶操作, 其定义准则为: 如果聚类内像素个数小于给定阈值 c, 则直接删除该类; 如果聚类内像素个数大于给定 阈值 n, 则在该类中随机选取一个像素作为生成新 聚类的聚类中心. 如果所有聚类均满足上述准则, 则 利用 FLICM 算法优化该结果, 以便为聚类分裂合并 操作提供粗分割结果. 由于采用的 FLICM 算法为基于模糊的分割方 法,其像素可以隶属于所有类别,定义第j 个聚类的模 糊平均距离为 i=1 dj = N∑ c∑ uijjjxi vjjj2 N∑ / c∑ uij i=1 d = uijdj uij; j=1 j=1 ; (5) (6) 定义全局模糊平均距离为 聚类的标准差矢量为 N∑ i=1 vuuuuuuuut j = uij(xi vj)2 N∑ uij i=1 ; j = 1; 2; ; c: (7) 对于每个聚类, 求出其类内标准差矢量 j 中的最大 分量 max = fjjj = 1; 2; ; cg: (8) 基于欧氏距离定义各聚类中心距离为 Djj′ = ∥vj vj′∥2; ′ = j + 1; j + 2; ; c: j = 1; 2; ; c 1; j (9) 对于任意类别 j, 如果类内模糊平均距离大于全 局模糊平均距离, 类内标准差大于给定阈值, 且类内 像素个数大于给定每类的最大像素数, 即满足条件 dj > d,max > s,nj > n, 其中 nj 为第 j 个聚类内的
    264 控 制 与 决 策 第32卷 像素数, 则认为该聚类在特征空间中聚集程度不足, 聚类范围过大, 需要进行分裂操作. 此外, 如果聚类数 不大于期望聚类数的一半, 即 c ⩽ e/2, 其中 e 为期望 聚类数, 则表明聚类数过少, 同样需要对其进行分裂 操作. 鉴于FLICM 算法利用聚类中心描述不同聚类, 将聚类中心看作分裂合并的操作对象. 假设第 j 类满 足分裂条件,将vj 分裂成v+ j ,有 j 和v 8<: v+ v j = vj + j; j = vj j; (10) 其中 需保证新的聚类中心在原聚类内部. 因为 需 人为给定, 而不同图像, 甚至不同聚类都对应不同的 最优 值, 难以在有效区分聚类中心的同时保证分裂 后的聚类中心在分裂前的聚类内. 所以, 在进行分类 操作后, 利用FLICM 算法对现有分裂结果进行优化. 该优化过程不但能够解决 值选定困难的问题, 还能 够稳定分裂结果. 此外, 为了避免算法陷入局部极值, 计算分裂后的目标函数,若分裂后的目标函数值小于 分裂前, 则接受该分裂; 若分裂后的目标函数值大于 分裂前, 但相差不多, 则通过接受率给定该分裂一个 被接受的机会, 以避免算法陷入局部极值; 若分裂后 目标函数值远大于分裂前, 则拒绝此次分裂. 为了简 化算法, 随机生成一个接受率, 当接受率大于阈值时 接受本次操作, 否则拒绝本次操作. 可接受的目标函 数值之差越大、接受率阈值越大, 算法越不容易收敛; 相反, 可接受的目标函数值之差越小、接受率越小, 算 法越容易陷入局部极值. 因此, 设定目标函数值之差 不超过原值的 5%, 接受率阈值为 0.6, 保证算法能够 跳出局部极值的同时达到快速收敛的目的. 此外, 为 了实现算法的自适应性,降低阈值选取对分割结果的 影响,将稳定的分裂结果的最大标准差赋予表征标准 差的阈值s,将目前最大聚类的像素数赋予表征类内 像素数阈值n,类内最少像素数赋予阈值c. 给定任意两个类别, 如果两个聚类中心间的距 离小于给定阈值 d, 则表明两个聚类中心距离较近, 应进行合并操作. 此外, 如果聚类数不小于 2 倍的期 望聚类数, 即 c ⩾ 2e, 则表明现有聚类中心过多, 需 进行合并操作. 将式(9) 按增序排列, 如果其最小距离 ), 即 小于给定阈值(假设最小聚类对应索引为 j+, j Dj+j < d, 则合并这两个聚类, 合并操作对象依旧 为聚类中心. 假设合并后其聚类索引为 j, 其聚类中心 vj 可通过下式计算: vj = 1 n+ j + n j (n+ j v+ j + n j v j ); (11) j ,n j 表示第 j+ 类和第 j 类的像素个数. 同理, 其中 n+ 在合并操作结束后, 利用 FLICM 算法对该合并结果 进行优化, 并判定该操作是否被接受, 然后将优化后 两个聚类中心的最小距离赋予阈值d,以实现参数阈 值的自适应性. 由于该算法属于可变类算法,需要不断地进行分 裂合并操作, 需要定义一个停止条件. 通常认为算法 同时不满足分裂合并条件时达到收敛,但是其收敛性 没有明确定义, 因此记录每次分裂合并后的聚类数, 并构建一个聚类数序列,当该序列内的聚类数不再变 化时认为算法收敛. 实验表明, 连续6 或7 次迭代聚类 数不再改变时, 算法收敛. 但为了保证其收敛性, 选取 10 为序列长度, 即聚类数连续10 次不再改变时, 认为 算法达到稳态. 参数主要可分为如下几类: 分类合并相关(c,n, s,d)、图像相关(e,c)和算法相关(I). 其中: 分类合并 相关的4 个参数可以通过上述自适应方法自动确定; 图像期望聚类数只需保证真实聚类数落在 e/2s2e 之间, 是否接近其真实值不影响最终聚类数估计结 果; 模糊聚类算法中最大迭代次数一般为 100 次. 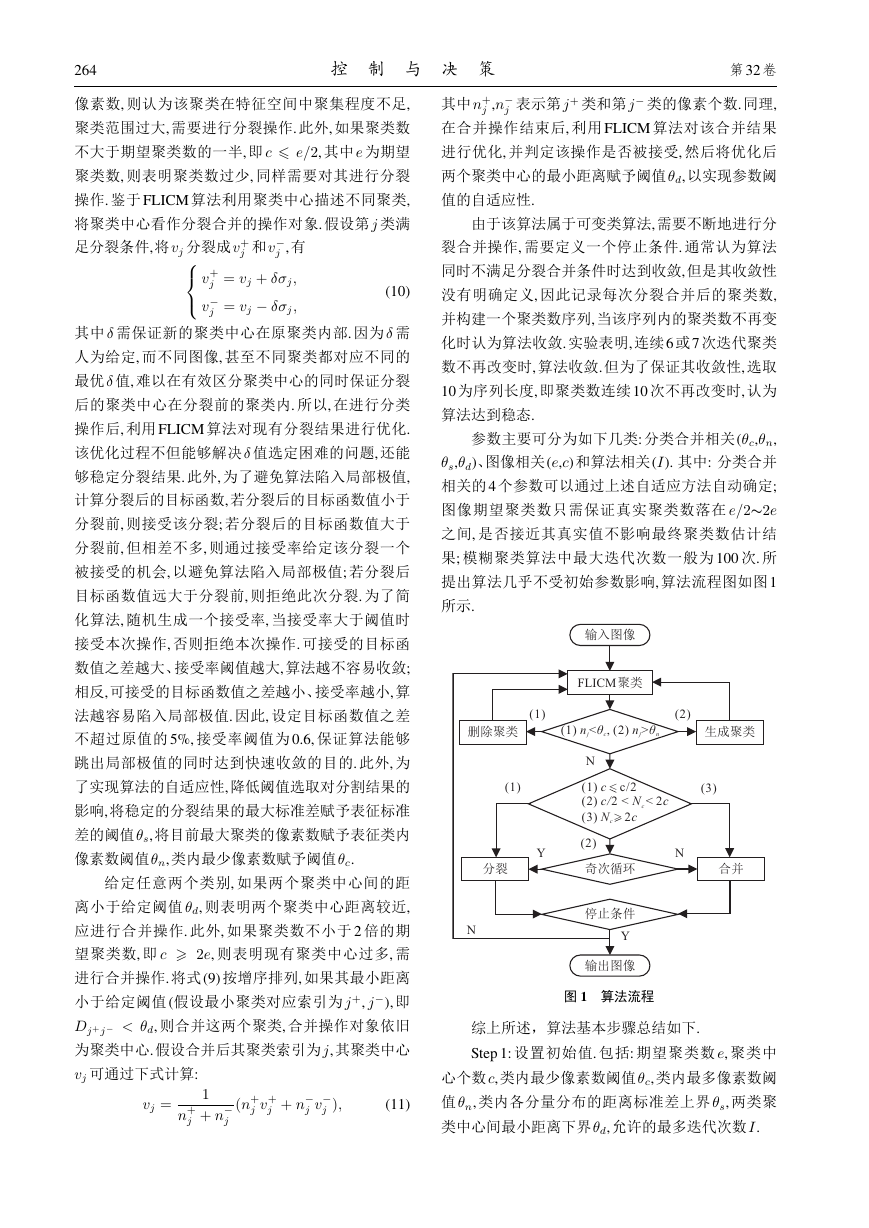所 提出算法几乎不受初始参数影响, 算法流程图如图1 所示. 图 1 算法流程 综上所述，算法基本步骤总结如下. Step 1: 设置初始值. 包括: 期望聚类数 e, 聚类中 心个数 c, 类内最少像素数阈值 c, 类内最多像素数阈 值 n, 类内各分量分布的距离标准差上界 s, 两类聚 类中心间最小距离下界d,允许的最多迭代次数I. ((2)>njnθ1)<,njcθ((2)2< 2(3)> 2c/< NcNccc1)< c/2c᜻Iǹᩩ382ᐭ82FLICM̥ᑤ◀̥˯ᡂ̥ᔠᑖXYNYN(1)(3)(1)(2)N(2)
    第2期 赵雪梅 等: 参数自适应的可变类 FLICM 灰度图像分割算法 265 Step 2: 初始化聚类中心 v(0) , 由式 (3) 和 (4) 利用 FLICM 算法计算每个像素的模糊隶属度和各聚类中 心矢量,得到稳定的分割结果. j Step 3: 计算每类的像素个数 n(t). 若 n(t) j 小于 c, j 大于 n, 则 则删除该聚类中心, 并返回 Step 2; 若 n(t) 在该聚类内随机生成一个聚类中心,并返回Step 2. Step 4: 判断聚类中心个数 c 的取值范围. 若 c ⩽ e/2,则进行上述分裂操作;若c ⩾ 2e,则进行上述合并 操作; 若 e/2 ⩽ c ⩽ 2e, 则为了保证实现聚类数的变 化, 需给定算法一个分裂合并的机会, 假设迭代次数 为奇数时进行分裂操作,迭代次数为偶数时进行合并 操作. 图 3 模板图像和模拟图像 Step 5: 利用式(3)重新计算聚类中心. Step 6: 如果迭代次数大于最大迭代次数, 或者迭 代过程收敛,则结束迭代,否则, 返回Step 3继续迭代. 2 实验分析 2.1 模拟图像分割 为了验证所提出算法的有效性,生成一幅模拟图 像, 假定模拟图像服从高斯分布(各个区域的均值和 方差如表1 所示). 图2 为各同质区域的概率密度函数 (pdf) 曲线. 由表1 数据可见, 区域I 方差为30, 区域III 和区域 V 的方差均为 20. 由于这 3 个区域方差较大, 结合图2,3 个区域的灰度值有较大重叠部分, 位于重 叠区域内的灰度值很难通过传统手段分割开来.区域 II 和区域IV 的方差均为10, 由图2 可见, 这两个区域 与其他区域的重叠部分明显较少,理论上更容易区分 开来. 以图3(a) 为模板图像, 将上述高斯分布加入模 板图像得到每个区域服从不同高斯分布的模拟图像, 如图3(b)所示. 表 1 高斯分布的均值和方差 同质区域 I 均值 方差 160 30 II 40 10 III 200 20 IV 80 10 V 120 20 图 2 同质区域分布曲线 图 4 模拟图像及其分割结果 0100200300gray levelIIIIIIVIV00.010.020.030.04pdfIIIIIIIVV(a)ʥ82(b)>82(a)ISODATAᑖᒘʧ(b)ISODATA-FLICMᑖᒘʧ(c)ᡠ?3ᑖᒘʧ
    266 控 制 与 决 策 第32卷 为验证所提出算法的分割精度和对聚类数判别 的准确性, 分别利用所提出算法与可变类 ISODATA 算法和结合FLICM 算法的ISODATA 算法(ISODATA -FLICM) 进行对比. 对图 2(b) 模拟图像进行分割实 验, 得到如图 4 所示的分割结果 (其中 ISODATA 和 ISODATA-FLICM 算法的分割结果为经过多次实验、 不断调整相关参数得到的 5 类分割结果). 相关参数 设置如下: c = 1 000, n = 5 000, s = 17, d = 20, e = 3, c = 4. 素混淆. 其主要原因是 IOSODATA 算法采用 K 均值 算法获取分割结果, K 均值算法只考虑像素本身对 分割结果的影响, 对噪声和异常值敏感, 而FLICM 算 法充分考虑像素间的相互作用关系,能够有效去除噪 声. 因此, ISODATA-FLICM 算法和所提出算法均能 够获得较好的分割结果. 表 2 为传统 ISODATA 算法、 ISODATA-FLICM 算法和所提出算法分割结果的混 淆矩阵. 由于传统 ISODATA 算法受噪声影响较为严 重, 导致其分割结果(图4(a)) 中包含大量误分像素, 除 区域 II 外, 其他各区域产品精度和用户精度均不高. 区域II 产品精度明显高于其他区域的主要原因是区 域 II 均值与其他区域相差较大, 且像素灰度值与其 他区域交叉较少. 由于 ISODATA 算法和 ISODATA- FLICM 算法类别数均通过反复实验得到, 而分割精 度主要取决于分割算法精度, ISODATA-FLICM 算法 和所提出算法的分割结果几乎完全相同,对各个区域 的分割精度较传统 ISODATA 算法均有较大的改善, 用户精度、产品精度均明显高于传统ISODATA 算法, 总精度由71.9%提高到了92.6%. 表 2 ISODATA 算法、ISODATA-FLICM 算法和所提出算法分割结果的混淆矩阵 由图 4 可见, 传统 ISODATA 算法的分割结果中 包含大量分割噪声, 区域 II 和区域 IV 的分割结果略 优于区域 III 和区域 V, 区域 I 的分割结果最差. 结合 表 1, 区域 II 和区域 IV 的方差最小, 因此分割结果较 好. 再结合图3, 区域IV 与区域Vpdf 的交叉部分略多 于区域 II 与区域 IV 的交叉部分, 因此区域 II 的分割 结果略优于区域IV. 区域I 方差最大, 且其pdf 与区域 III 和区域 V 的 pdf 交叉部分像素灰度级较多, 因此, 单纯地考虑像素自身对分割结果的影响导致传统 ISODATA 算法容易将区域 I 与区域 III、区域 V 的像 ISODATA 算法/ISODATA-FLICM 算法/所提出算法 I II III IV V 总数 产品进度/% 1 590/3 117/3 117 72/88/88 986/74/74 80/108/108 213/1/1 2 941/3 388/3 387 54.1/92.0/92.0 I II III IV V 486/33/34 116/0/0 0/0/0 2 971/2 916/2 916 0/0/0 171/0/0 54/28/28 2 169/3 115/3 115 61/31/31 9/0/0 2/0/0 3 151/2 916/2 916 94.3/100.0/100.0 2 772/3 207/3 208 78.3/97.1/97.1 79/127/127 52/0/0 2 919/3 021/3 021 645/2/2 3 811/3 150/3 150 76.6/95.9/95.9 1 123/165/165 138/155/155 172/190/196 145/216/216 2 131/2 997/2 997 3 709/3 723/3 723 57.5/80.5/80.5 总数 3 315 3 314 3 379 3 376 3 000 16 384 用户精度/% 48.0/94.0/94.0 89.7/88.0/88.0 64.2/92.2/92.2 86.5/89.5/89.5 71.0/99.9/99.9 总精度/% 71.9 / 92.6 / 92.6 虽 然 对 模 拟 图 像 的 分 割 精 度 分 析 表 明 ISODATA-FLICM 算法和所提出算法的分割结果精 度并没有明显差别, 但实际上, 传统ISODATA 算法和 ISODATA-FLICM 算法很难将模拟图像分成 5 个类 别,其聚类数的估计主要依赖于控制聚类分裂合并的 阈值. 但是, 不同图像需要不同的阈值才能得到其最 优聚类数, 且算法需要设定多个阈值, 而不同阈值组 合仍会影响其最终分割结果. 因此, 在这种情况下, 采 用ISODATA 算法和ISODATA-FLICM 算法分割影像 不具有实际应用价值.所提出算法结合模糊集理论设 计基于聚类中心的分裂合并操作,并设计接受率避免 算法陷入局部极值的同时保证算法趋于最优,进而在 此基础上自适应地估计待分割图像的聚类数. 因此, 所提出算法不但能够准确估计图像聚类数,同时还能 得到较好的分割结果. 在算法运行速度上,所提出算法容许在一次循环 内进行多次分裂合并操作直至其结果不再满足分裂 或合并条件, 在每次分裂合并后利用 FLICM 算法对 其结果进行优化, 使算法更容易逼近其最优分割结 果, 进而极大程度地提高了算法的运行速度. 此外, 由 于所提出算法记录算法迭代的聚类数,并认为当聚类 数连续 10 次不再改变时算法收敛, 有效避免了给定 不同迭代上限造成的图像迭代不充分或者过度迭代 的问题, 有效提高了算法的运行效率. 算法运行环境 为Core i5,主频1.90GHz, RAM 4.00 GB, Matlab 2012b. 传统ISODATA 和ISODATA-FLICM 算法的运行速度
    第2期 赵雪梅 等: 参数自适应的可变类 FLICM 灰度图像分割算法 267 约为10s,所提出算法的运行时间为4 s. 2.2 真实图像分割 选取3 幅真实灰度纹理图像如图5s 图7 所示, 目 视判别其聚类数分别为3、3、4;传统ISODATA算法的 聚类数分别为4、4、5; ISODATA-FLICM 算法的聚类 数分别为4、4、5; 所提出算法的聚类数分别为3、3、4. 传统 ISODATA 算法采用 K 均值聚类算法实现图像 分割, 只考虑像素本身的灰度特征, 无法有效消除噪 声影响, 分割结果略差于其他两种算法.ISODATA- FLICM 算法采用分割精度更高的 FLICM 算法, 分割 结果略优于传统ISODATA 算法. 但是, 这两种算法均 无法准确判别图像聚类数,基于不准确的聚类数得到 的分割结果不够理想. 所提出算法基于 FLICM 算法 用聚类中心描述分割的特征,设计基于聚类中心的分 裂合并操作,并通过接受率使算法趋于最优的同时避 免算法陷入局部极值,进而随算法趋于最优自适应参 数阈值, 最终实现聚类数的准确估计, 并获得相应聚 类数下的最优分割结果. 因此, 所提出算法分割结果 不但在聚类数估计上优于其他两种算法,还能够获得 更加准确的图像分割结果. 图 5 纹理图像及其分割结果(一) 图 6 纹理图像及其分割结果(二) 图 7 纹理图像及其分割结果(三) 3 结 论 本文为解决传统FLICM 算法需人为给定图像聚 类数的问题, 提出了参数自适应的可变类 FLICM 灰 度图像分割算法. 以FLICM 算法为基础, 设计了基于 模糊集理论和图像特征空间聚类特征的分裂-合并操 作, 并在每次分裂-合并后根据图像参数改变聚类尺 度阈值,具有以下优点: 1) 能够准确估计图像的聚类数. 算法结合模糊集 理论设计以聚类中心为操作对象的分裂-合并操作, 充分利用了FLICM 算法通过聚类中心描述图像分割 的特性, 准确估计图像聚类数. 此外, 通过接受率的设 计以及参数的自适应,进一步提高了其聚类数估计的 准确性. 2) 较之现有的分割算法, 具有更快的运行速度. (b)ISODATAᑖᒘʧ(c)ISODATA-FLICMᑖᒘʧ(d)dᡠ?3ᑖᒘʧ(a)ᳮ82(b)ISODATAᑖᒘʧ(c)ISODATA-FLICMᑖᒘʧ(d)dᡠ?3ᑖᒘʧ(a)ᳮ82(b)ISODATAᑖᒘʧ(c)ISODATA-FLICMᑖᒘʧ(d)dᡠ?3ᑖᒘʧ(a)ᳮ82
    268 控 制 与 决 策 第32卷 算法容许在一次迭代内进行多次分裂或合并操作,并 在每次操作结束后对其结果进行优化,有效提高了算 法的运行速度. 3) 能够避免算法陷入局部极值. 在每次分裂合并 后, 计算其目标函数值并与分裂合并前进行比较, 设 计接受概率以接受不甚满意的分割结果,从而避免算 法陷入局部极值. 4) 实现了参数的自适应. 在每次分裂合并后根据 现有分割结果重新赋予相关阈值, 实现了分裂-合并 操作阈值的自适应性. 将 所 提 出 的 算 法 与 传 统 ISODATA 算 法 以 及 ISODATA-FLICM算法进行对比实验,结果表明,所提 出算法不但能够实现高精度分割,还能够通过自适应 的分裂合并操作准确确定图像的聚类数. 此外, 由于 所提出算法实现了参数的自适应性,有效避免了传统 可变类算法人工选择参数对分割结果影响较大的问 题. 参考文献(References) [1] 王晓年, 冯远静, 冯祖仁. 一种基于主动轮廓模型的 蚁群图像分割算法[J]. 控制理论与应用, 2006, 23(4): 515-522. (Wang X N, Feng Y J, Feng Z R. Ant colony optimization with activbe contour models for image segmentation[J]. Control Theory & Applications, 2006, 23(4): 515-522.) [2] 毕凯, 王晓丹, 邢雅琼. 基于模糊测度和证据理论 的模糊聚类集成方法 [J]. 控制与决策, 2015, 30(5): 823-830. (Bi K, Wang X D, Xing Y Q. Fuzzy clustering ensemble based on fuzzy measure and DS evidedence theory[J]. Control and Decision, 2015, 30(5): 823-830.) [3] Bezdek J. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum, 1981: 79-88. [4] Krinidis S, Chatzis V. A robust fuzzy local information C-means clustering algorithm[J]. IEEE Trans on Image Processing, 2010, 19(5): 1328-1337. [5] 常发亮, 刘静, 乔谊正. 基于遗传算法的彩色图像二 维熵多阈值自适性分割[J]. 控制与决策, 2005, 20(6): 674-678. (Chang F L, Liu J, Qiao Y Z. Self-adaptive threshold segmentation for color image using two-dimednsional entropy method based on genetic algorithm[J]. Control and Decision, 2005, 20(6): 674-678.) [6] 朱付平, 田捷, 林瑶, 等. 基于Level Set 方法的医学图 像分割[J]. 软件学报, 2002, 13(9): 1866-1872. (Zhu F P, Tian J, Lin Y, et al. Medical image segmentaiton based on Level Set method[J]. J of Software, 2002, 13(9): 1866-1872.) [7] 向日华, 王润生. 一种基于高斯混合模型的距离图像 分割算法[J]. 软件学报, 2003, 14(7): 1250-1257. (Xiang R H, Wang R S. A range image segmentation algorithm based on Gaussian mixture model[J]. J of Software, 2003, 14(7): 1250-1257.) [8] Ball G H, Hall D J. A clustering technique for summarizing multivariate data[J]. Behavioral Science, 1967, 12(2): 153-155. [9] Bezdek J C. Cluster validity with fuzzy sets[J]. J of Cybernetics, 1974, 3(3): 58-73. [10] Dunn J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. J of Cybernetics, 1973, 3(3): 32-57. [11] 黄敏, 李凤娥, 孙艺红, 等. 电子商务环境下基于模 糊ISODATA 聚类法的企业风险分类[J]. 控制与决策, 2004, 19(2): 179-182. (Huang M, Li F E, Sun Y H, et al. Fuzzy ISODATA cluster based risk sorting for enterprise under EC environments[J]. Control and Decision, 2004, 19(2): 179-182.) [12] 张语涵, 孙劲光, 苗锡奎. 基于改进的 ISODATA 算 法彩色图像分割 [J]. 计算机系统应用, 2010, 19(2): 41-45. (Zhang Y H, Sun J G, Miao X K. Color image segmnetaion based on improved ISODATA[J]. Computer Systems and Applications, 2010, 19(2): 41-45.) [13] 马彩虹, 戴芹, 刘士彬. 一种融合PSO 和ISODATA 的 遥感图像分割新方法[J]. 武汉大学学报信息科学版, 2012, 37(1): 35-38. (Ma C H, Dai Q, Liu S B. A new method of remote sensing image segmentaiton based on PSO and ISODATA[J]. Geomatics and Information Science of Wuhan University, 2012, 37(1): 35-38.) [14] 袁传虎, 吴晓红, 王正勇, 等. 一种融合Canny 和改进 ISODATA 的砾岩图像分割算法[J]. 计算机工程与应 用, 2012, 48(10): 175-178. (Yuan C H, Wu X H, Wang Z Y, et al. Conglomerate image-segmentation method based on combining Canny and imoproved ISODATA algorithm[J]. Computer Engineering and Applications, 2012, 48(10): 175-178.) （责任编辑：郑晓蕾）
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料