logo资料库

参数优化GA-ELM模型在露天煤矿抛掷爆破的预测.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.86M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    第 42 卷第 3 期 2017 年 3 月 煤 炭 学 报 JOUＲNAL OF CHINA COAL SOCIETY Vol．42 No．3 Mar． 2017 温廷新，陈晓宇，邵良杉，等．参数优化 GA－ELM 模型在露天煤矿抛掷爆破的预测［J］． 煤炭学报，2017，42( 3) :630－ 638． doi:10． 13225 / j．cnki．jccs．2016．0572 Wen Tingxin，Chen Xiaoyu，Shao Liangshan，et al． Prediction on parameters optimized GA-ELM model for cast blasting in open-pit mine ［J］．Journal of China Coal Society，2017，42(3) :630－638．doi:10．13225 / j．cnki．jccs．2016．0572 参数优化 GA－ELM 模型在露天煤矿抛掷爆破的预测 温廷新1 2，陈晓宇1，邵良杉1，窦 融2，魏 鹏2 ， (1. 辽宁工程技术大学 系统工程研究所，辽宁 葫芦岛 125105;2. 辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105) 摘 要: 为有效指导露天煤矿制定正确生产计划，提高露天煤矿抛掷爆破预测的准确率，在分析露 天煤矿抛掷爆破影响因素的基础上，通过“试错法”确定模型最优隐含层节点参数，进而提出一种 参数优化后遗传算法( GA) 和极限学习机( ELM) 相结合的抛掷爆破预测模型。选取网络的输入输 出相关参数，针对现有 ELM 输入权值矩阵和隐含层偏差，采用遗传算法对其进行优化选择; 利用某 露天煤矿抛掷爆破监测数据对该模型进行实例分析，并将 ＲBF，BP，SVM，GA－BP 模型预测结果与 该模型进行对比分析; 并引入 Weibull 模型，通过预测控制参数 ɑ，β 模拟爆堆形态。研究结果表 明: ① 通过“试错法”确定 GA－ELM 模型最优隐含层节点数为 39，有效降低系统的仿真误差，该参 数下仿真误差值为 0. 137 7; ② 相较于传统 ELM 预测模型，通过遗传算法优化后，有效抛掷率，松 散系数以及抛掷距离均得出更小的均方误差 MSE 值( 0. 258 0，1. 748 5×10－4，3. 618 4) 和更高的决 定系数 Ｒ2值( 0. 986 4，0. 995 3，0. 970 6) ，改进后的 GA－ELM 具有更好的拟合效果和泛化能力; ③ 通过与其他智能算法如 BP，ＲBF，SVM，GA－BP 相比，改进后的 GA－ELM 测试结果( 均方误差，决定 系数，仿真误差) 明显优于其他预测模型，有效提高预测精度; ④ 利用训练完成的 GA－ELM 网络预 测爆堆形态时，控制参数 a，β 的预测误差均未超过 5%，预测爆堆曲线接近真实爆堆曲线。 关键词: 露天煤矿; 抛掷爆破; 预测; GA－ELM 模型; 试错法 中图分类号: TD824. 3 文章编号: 0253－9993( 2017) 03－0630－09 文献标志码: A Prediction on parameters optimized GA-ELM model for cast blasting in open-pit mine WEN Ting-xin1，2，CHEN Xiao-yu1，SHAO Liang-shan1，DOU Ｒong2，WEI Peng2 (1．System Engineering Institute，Liaoning Technical University，Huludao 125105，China;2．School of Business Administration，Liaoning Technical University， 125105，China) Huludao Abstract:In order to make a correct production plan effectively and improve the accuracy of cast blasting in open-pit mine，based on the analysis of cast blasting factors，the optimized hidden layer node parameters are determined by“tri- al-and-error”and then one kind prediction model is proposed with the combination of Genetic Algorithm ( GA) and Extreme Learning Machine ( ELM) ．On the basis of network input and output parameters’selection，the optimization and selection are made using GA for ELM model’s input weight matrix and hidden layer deviation．Using a cast blas- ting monitoring data in an open-pit mine，the model analysis was conducted，then the prediction results of ＲBF，BP， SVM，and GA-BP models were compared with the model results．In addition，Weibull model was introduced to simulate the coal blasting form by predicting control parameters a，β． The results show that:① The optimal hidden layer node 收稿日期: 2016－05－04 基金项目: 国家自然科学基金资助项目(71371091) ;辽宁省社科基金资助项目( L14BTJ004) 作者简介: 温廷新(1974—) ，男，山西太谷人，教授，硕士生导师，博士研究生。E－mail:wen_tx@ 163. com。通讯作者: 陈晓宇( 1993—) ，男，硕 修回日期: 2016－09－14 责任编辑: 许书阁 士研究生。E－mail:chenxy93@ qq. com 中国煤炭期刊网 www.chinacaj.net
    第 3 期 温廷新等:参数优化 GA－ELM 模型在露天煤矿抛掷爆破的预测 136 number is 39，which reduces the system simulation error effectively，and the simulation error is 0．137 7;② Compared with traditional ELM prediction model，after optimized by GA，Effective Casting Blasting Ｒatio，Loose Coefficient and Cast Distance all have lower Mean Square Error ( MSE:0．258 0，1．748 5×10 －4，3．618 4) and higher Decision Coeffi- cients ( Ｒ2:0．986 4，0．995 3，0．970 6) ．Improved GA-ELM model has a better fitting effect and generalization ability; ③ Compared with other intelligent algorithm，such as BP，ＲBF，SVM，GA-BP，the test set results ( MSE，Ｒ2，SE) of improved GA-ELM model are much better and improve the prediction accuracy effectively;④ Using trained GA-ELM network to predict coal blasting form，the prediction error of control parameters a and β are not more than 5% and the prediction of blasting heap curve is close to the real blasting heap． Key words:open-pit mine;cast blasting;prediction;GA-ELM model;trial-and-error 在露天煤矿开采中应用高台阶抛掷爆破技术，可 以降低开采过程中的剥离成本———在无需进行采， 运，排作业的情况下，直接将 30% ～ 60% 的剥离物抛 掷到采空区，减少拉斗铲剥离量。因此，深度挖掘露 天煤矿抛掷爆破监测数据的时变规律，通过智能方法 准确预测露天煤矿抛掷爆破变化趋势，对于露天煤矿 抛掷爆破具有十分现实的经济意义。 目前，国内有关论述露天煤矿抛掷爆破抛掷的 文献仍为数不多。近年来，大多数学者关于露天煤 矿抛掷 爆 破 预 测 与 模 拟 的 研 究 主 要 集 中 为 两 类。 一种是通过 力 学 模 型 进 行 理 论 分 析 和 现 场 试 验 探 讨露天煤矿抛掷爆破效果:自 2006 年开始，李克民 等采用理论结合经验公式的方法，并结合 D’Appo- lonia“图解 法 ”最 终 对 抛 掷 爆 破 参 数 作 出 优 化 分 析［1］;周伟等利用弹道理论以及露天采矿学的基本 原理，建立了抛掷速度反演模型和有效抛掷率离散 模型［2］;李祥龙等通过理论分析和露天煤矿现场实 面的预测分析。此外，由于 BP 神经网络具有易陷入 局部最优、收敛速率慢，训练样本需求大等局限性，用 其对抛掷爆破进行预测所得结果误差较大，并不理 想;而 SVM 模型核函数参数以及参数惩罚项的选择、 优化均对 预 测 结 果 有 较 大 影 响; 鉴 于 此，笔 者 结 合 ELM 算法 训 练 速 度 快，泛 化 能 力 好 等 优 点，采 用 GA( 遗传算法) 优化 ELM( 极限学习机) 输入权值矩 阵 和 隐 含 层 偏 差，对 露 天 煤 矿 抛 掷 爆 破 进 行 预 。 测［9－12］ 1 GA－ELM 基本理论 1. 1 ELM 基本原理 极限学习机 ( ELM) 算法是 2004 年南洋理工大 学黄广斌副教授提出来的一种网络学习算法，其本质 上属于典型的的单隐层前馈神经网络。但相较于传 统的单隐层前馈神经网络，ELM 克服了传统梯度算 法易陷入局部极值的局限性，具有学习速度快，分类 验，研究台 阶 高 度 对 抛 掷 爆 破 效 果 的 影 响［3］;马 力 准确 率 准 确 率 高，泛 化 能 力 好，调 节 参 数 少 等 优 等在弹道理论和平面药包法的理论基础上对( 炸药 点［13－16］ 。 单耗，炮 孔 倾 角) 与 抛 掷 距 离 的 关 系 展 开 深 入 研 究［4］;另一种 是 以 抛 掷 爆 破 相 关 数 据 为 基 础，结 合 智能化数学模型展开分析预测:如刘希亮等提出遗 传算法优化 的 支 持 向 量 机 模 型 对 抛 掷 爆 破 有 效 抛 掷率进行 预 测［5］;孙 文 希 等 以 抛 掷 爆 破 台 阶 高 度、 孔距等参数的 MIV 值作为评价依据，研究输入参数 对抛掷距离等输出参数的影响权重［6］;孙文希等通 过设置不同参数，研究 BP 神经网络的收敛速度和 其预测结果的准确性，并与 ＲBF，SVM 预 测 模 型 的 结果进行对比［7］;刘干等在分析了抛掷爆破有效抛 掷率影响因素的基础上，通过广义回归神经网络建 立有效抛率预测模型［8］ 。 在上述学者的研究中，大多以单评价因子建立预 测模型。本文综合考虑有效抛掷率，松散系数，抛掷 距离 3 项重要指标，并通过预测 Weibull 模型控制参 数模拟爆破堆形态，对露天煤矿抛掷爆破进行更为全 ELM 实现的过程，对于 N 个任意的各不相同的 样本( xi xi = ［xi1 ，yi ，xi2 ) ，其中 ，…，xin ］T "Ｒm 则前馈神经网络激励函数为 g( x) ，隐含层节点 ］T "Ｒn;yi = ［yi1 ，…，yin ，yi2 数为 L 时，输出可以表示: L i = 1 fL ) ， β i G( ai·xi + bi ( x) = ∑ x ∈ Ｒn，ai ∈ Ｒn，β i ∈ Ｒm ，ai2 (1) ］T 为输入层到隐含层节点 i ， ，βi2 表 ］T 为连接隐含层节点 i 的输出权值;ai ·xi 为第 i 个隐含层节点的阈值;β i =［βi1 ，…，ain 式中，ai =［ai1 的输入;bi …，βim 示向量 ai 和 xi 的内积。 G( x ) 为 激 励 函 数，可 以 采 用 ”ＲBF ”，”Sine ” 或”Sigmoid”等。 如果这个隐含层节点数为 L 的前馈神经网络能 以误差 0 逼近 N 个样本，则 ai ，bi ，β i 存在关系如下: 中国煤炭期刊网 www.chinacaj.net
    煤 炭 学 报 2017 年第 42 卷 236 fL L ( x) = ∑ i = 1 β i G( ai * xi + bi i = 1，2，…，L ) = yi ， (2) 式(2) 可简化为:Hβ = Y'，式中，     H( a1 ，…，aL g( a1* x1 + b1 ，…，bL ，b1 ，…，xN ) = ) ) … g( a1* x1 + bL ，x1 … … … g( a1* xN + b1 β = ) β T 1 ) … g( a1* xN + bL     ，T =  yT  β T             yT 1 L L     N ×L H 为隐含层的输出矩阵。一旦 ELM 算法中输出 权值和阈值被随机确定，隐层的输出矩阵 H 就变成 惟一确定的。而训练前馈神经网络就可以转化成一 个求解线性系统最小二乘解的问题。输出权重 β 也 可以被确定:β^ = H'Y，其中，H'是矩阵 H 的 Moore － Penrose 广义逆。 传统 ELM 算法的流程如下: Step 1:随机给定网络输入隐含层权值 αi ，i = 1，…，L:其中隐含层节点个数为 L; Step 2:选择隐含层神经元的激活函数为一个无 以及阈 值 bi 限可微的函数，并对隐含层输出矩阵 H 计算; Step 3:计算网络隐含层节点与输出节点之间的 的连接权值 β^ :β^ = H'Y。 1. 2 GA 优化 ELM 预测模型 随机给定 ELM 的输入权值矩阵和隐含层偏差， 可能部分数值为 0，使得一些隐含层节点失效，为达 到预计精度只有提高隐含层节点的数目。但随之带 来模型 对 未 知 样 本 适 应 能 力差，导 致 泛 化 能 力 低 下［17－20］ 。针对上述问题，本文采用遗传算法对极限 学习机中输入层权值和隐含层偏差进行优化选择 。 训练步骤如下: (1) 产生种群。种群个数 N 一般设置为 20 ～ 40， 种群中的个体是由输入权值矩阵和隐含层偏差构成， 个体长度为 L = ( n + 1) k，式中，k 为隐含层节点数;n 为输入层神经元数，即输入向量维数。 (2) 对种群中的任一个体，采用 ELM 算法( 隐含 层激活函数为 Sig 函数) 计算输出权值矩阵，通过代 入 P _train 计算，得出初始化种群每个个体的分类准 确率，将该参数作为遗传优化算法的适应度。计算种 群第 1 个个体 θ1 的适应度值 Fitness_1，将 Fitness_1 赋值给最优适应度 Fitness_best;并将 θ1 作为 pBest;然 后执行以下伪代码: Step 1:for i = 1:N { 计算 θi的适应度值 Fitness_1 If Fitness _ 1 ＞ Fitness _ best then pBest( i)= θi Else pBest( i)= θi－1} 令 Fitness_i 对应的粒子 θ 为全局极值 gBest Step 2:for i = 1:P %P 为最大迭代次数 { 利用交叉，变异操作对当前群体进化; If 满足约束条件 or i＞P Break; Else loop Step 1 } (3) 执行上述 伪 代 码 流 程，计 算 出 最 优 适 应 度 所对应个体，即 ELM 算法所需的最优输入权值矩阵 和隐含层偏差，利用 ELM 算法继续求得输出权值矩 阵。 2 GA－ELM 预测模型因子选取 2. 1 影响因子选取 露天煤矿抛掷爆破是一种非线性的复杂动力系 统［21］，它时刻受地质条件、岩层性质、炸药特性等多 种因素影响而不断发生着变化。目前研究文献中，露 天煤矿抛掷爆破影响因素主要分为岩石性质、炸药特 性、爆破实施 3 类［1，5，22－25］ 。 由于露天煤矿地质构造及岩石特性较为单一，且 为提高开采效率大多选择岩性比较均匀的矿区，故在 本次研究中，笔者将岩性条件视为同质。此外，抛掷 爆破实施过程中通常采用相同的炮孔直径、炸药类 型、装药结构、炮孔堵塞方式等，因此，抛掷爆破优化 设计更多的是通过调整台阶高度、孔距、排距等地形 和设计参数来实现。 因此，笔者选取以下 10 个参数作为 GA－ELM 预 测模型的影响因子:炸药单耗、台阶高度、煤层厚度、 采空区上口宽、采空区下口宽、最小抵抗线、坡面角、 孔距、排距、剖面宽，如图 1 所示。 图 1 露天煤矿抛掷爆破影响因子 Fig. 1 Effective factors of cast blasting 2. 2 评价因子选取 有效抛掷率，松散系数，抛掷距离是反映露天矿 抛掷爆破效果的重要评价因子［5，7，24］，各参数计算示 意［4］如图 2 所示。 中国煤炭期刊网 www.chinacaj.net
    第 3 期 温廷新等:参数优化 GA－ELM 模型在露天煤矿抛掷爆破的预测 336 计算松散系数。 取 H( X) 为 Weibull 分布的概率密度函数，有 图 2 计算示意 Fig. 2 Calculation schemes 有效抛掷率 ηa 指 被 爆 岩 土 体 积 中 通 过 爆 破 技 术不需要 2 次转运直接抛掷到采空区或者坡下废 系数越大，被抛掷 石体积所占的百分比系数。该 ηa 到采空区的岩石量也就越大，拉斗铲的作业量也就 越小，降低了剥离成本。按图 2 所 示，即 为 A 部 分 岩石所占 A，B，C 部 分 岩 石 总 体 积 的 百 分 比，表 示 如下: ηa = VA / ( VA + VB + VC ) × 100% 松散系数 ηb 指爆破前后松散体积与岩石体积之 系数值影响着爆堆沉降高度、拉斗铲铲装 比。该 ηb 效率及辅助设备作业量等相关变量。按图 2 所示，即 为 A，B，C 部分作业后破碎岩石总体积与 C，D 部分 原石台阶岩体体积的比值，表示为 ηb = ( VA + VB + VC ) / ( VC + VD ) 抛掷距离 ηc 指从爆前自由面到爆后倒堆面之间 的水平距离，实际作业过程中利用爆后自由面数据与 倒堆面数据相交后的叠加面进行采集。该指标是保 证抛掷爆破安全性的重要指标之一。 鉴于此，并综合考虑前人相关研究，笔者选取抛 掷距离、松散系数及抛掷率作为本次 GA －ELM 露天 煤矿抛掷爆破预测模型的评价因子。 2. 3 Weibull 模拟爆堆形态预测参数选取 用 Weibull 分布模拟爆堆形态其难点在于 a，β 值的选取，a，β 是控制 Weibull 分布曲线形状的重要 参数。Weibull 分 布 模 型 理 论 是 1939 年 Weibull 提 出，以质量守恒定律为力学基础，被广泛应用于处理 各种随机现象的数量性特征［26］ 。 根据质量守恒定律，爆破前后岩体质量不变，即 lm ∫ 0 ρhh( x) dx = S0ρq (3) 分别为爆破前后岩石密度，kg / m3;h( x) 为 为待爆岩体的台阶剖面 ，ρh 式中，ρq 在 x 轴上的爆堆高度，m;S0 面积，m2;lm 为岩块最远抛距，m。 将式(3) 无量纲化，得到 lm ∫ 0 H( X) dX = 1 (4) 式中，X = x ，H = h ξS槡 0 ξS槡 0 ，Lm = lm ξS槡 0 ，ξ' = ρh ρq ，其中 ξ' 为 H( X) = 0 (      β α ( ) X α ) β － 1 (0 ≤ X ≤ Lm ) ( X ＞ Lmor X ＜ 0) [ exp － ) β ] (5) ( X α 其中，ɑ，β 为控制曲线形状的参数( β＞1) ，如果 ɑ，β 选择合理的话，H( X) 在 lm 出变化很小，则式( 4) 可以 H( X) dX = 1。 写成: ∫ +# －# 多排微差起爆的台阶爆破由于最后一排炮孔的 爆破漏斗作用，在所形成的爆堆中会出现一个漏斗状 的凹陷［27－28］ 。真实爆堆形态轮廓线与 Weibull 分布 曲线仅表现为主要部分符合。在利用 Weibull 模型 模拟爆堆形态需要通过无量钢化因子对真实的爆堆 形态曲线无量纲化，2 者位于同一坐标系下;式( 1) 无 量纲化的推导过程中，由 ξ = ρh / ρq ，可得无量纲化因 子为 1 。 根据现场统计资料和经验分析，确定爆 S0槡 ξ 破漏斗深度为(0. 17 ～ 0. 38) H'，H'为台阶高度。 3 实证分析 经 整 理，本 次 研 究 所 选 取 的 某 露 天 煤 矿 在 2009—2010 年共进行 16 次有效爆破作业成果，通过 对该矿区近年来的现场抛掷爆破实验进行数据搜集， 共获得了 188 组适用数据，选取其中 178 组观测数据 作为 GA－ELM 预测模型的训练数据，其余 10 组观测 数据作为测试样本数据。经整理计算，表 1 显示部分 输入参数。 3. 1 露天煤矿抛掷爆破 GA －ELM 预测模型参数优 化 本文应用遗传算法工具箱 Sheffield ［29］，相关参数 设置如下:个体编码方式为二进制编码并设置二进制 位数为 10，适应度函数采用排序的适应度分配函数: FitnV = ranking( obj) ，其中 obj 为预测样本的预测值 与期望值误差矩阵的范数，选择算子采用随机遍历抽 样，交叉算子采用单点交叉算子。遗传算法其他参数 分别设置为:种群个体数目 NIND 为 20，最大遗传代 数 MAXGEM 为 100，交叉概率 px 为 0. 7，变异概率 pm 为 0. 01，代沟 GGAP 为 0. 95。 ELM 算法，作为单隐层前馈神经网络的一种，如 何确定隐含层的神经元数目十分关键。隐含层神经 元数太少会导致 ELM 网络“欠适配”，而隐含层神经 元数太多会导致 ELM 网络“过适配”。为解决这个 中国煤炭期刊网 www.chinacaj.net
    436 剖面 编号 09e1－2 09e1－3 09e1－4 09e1－5 … 煤 炭 学 报 2017 年第 42 卷 表 1 GA－ELM 模型输入数据集( 部分) Table 1 Input data set of GA－ELM model ( part) 输入层参数 输出层参数 炸药单耗 / ( kg·m－3 ) 台阶高 度 / m 煤层 采空区 采空区 厚度 / 上口 下口 m 款 / m 宽 / m 抵抗 坡面 孔距 / 排距 / 剖面 有效抛 松散 线 / m 角 / ( °) m m 宽 / m 掷率 / % 系数 抛掷 距离 Weibull 分 布曲线控 / m 制参数 ɑ Weibull 分 布曲线控 制参数 β 计算松 散系数 ξ' 0. 72 0. 72 0. 72 0. 72 … 34. 61 28. 50 131. 38 95. 91 31. 40 30. 55 128. 37 92. 96 30. 60 35. 11 132. 99 99. 50 30. 36 30. 88 133. 50 98. 70 … … … … 8. 0 7. 0 7. 0 7. 0 … 56 59 63 66 … 11. 20 7. 11 66. 50 28. 2 1. 02 220. 99 1. 171 4 1. 076 9 1. 296 3 11. 00 8. 18 75. 11 35. 3 1. 07 202. 08 1. 110 2 1. 034 5 1. 511 1 11. 00 8. 25 74. 56 36. 7 1. 18 205. 89 1. 107 4 1. 091 3 1. 561 4 11. 01 8. 01 74. 19 33. 0 1. 19 197. 89 1. 116 9 0. 090 4 1. 511 5 … … … … … … … … 问题，往往需要设计者反复多次实验和根据自身经验 来确定。本文借鉴“试错法”的思想，为优化测试样 本的仿真误差，通过不断试验和连续地改变系统的隐 含节点参数，试验系统所作出的应答，进而寻求较优 的 GA－ELM 网络拓补结构。 综合以上情况，本文选取 GA －ELM 网络隐含层 单元数区间为［1，100］，测试该预测模型隐含层节点 数从 1 到 100，100 种不同情况下 GA－ELM 网络的仿 真误差，比较其拟合情况。输出模型仿真误差参数如 图 3 所示。 由于图 3 中试验结果无法精确选出最优参数，进 一步通过仿真误差值从上述试验结果中选取隐含层 节点参数较优的几种情况，再次进行 3 次重复测试， 见表 2。 图 3 抛掷爆破预测模型———“试错法”过程 Fig. 3 Prediction model of cast blasting-“trial-and- error”procedure 表 2 3 次重复测试结果比较 Table 2 Triplicate comparing test results 隐含层节点 13 18 23 34 39 47 57 63 83 测试第 1 次仿真误差 0. 334 1 测试第 2 次仿真误差 0. 149 9 测试第 3 次仿真误差 0. 160 5 0. 196 4 0. 334 1 0. 162 4 0. 096 3 0. 470 8 0. 613 4 0. 844 8 0. 364 9 0. 322 8 0. 621 4 0. 292 9 4. 93×10 －4 0. 907 0 0. 862 8 0. 315 7 0. 144 9 0. 189 9 0. 087 5 0. 209 2 0. 137 7 0. 367 2 0. 348 7 0. 668 7 0. 200 4 依 据 表 2 中 相 关 数 据 ，当 参 数 设 置 为 39 时 ， 系 统 仿 真 误 差 在 3 次 重 复 测 试 中 均 明 显 优 于 其 他 情 况 ，最 终 确 定 本 次预 测 模 型 隐 含 节 点 参 数 为 39 。 3. 2 GA－ELM 与 ELM 模型优化预测效果比较 将表 2 所得最优参数，作为 GA －ELM 网络的隐 含层节点数，并选择 Sig 为激活函数，代入训练样本 数据，通过多次试验，GA －ELM 预测模型经过 100 次 进化计算得到一个最佳适应度的稳定迭代值［30］如图 4 所示。 在确定最大遗传变异代数为 100 的基础上，进行 试验，获得最优的 GA －ELM 模型。训练样本的回代 准确率为 100%，决定系数 Ｒ2 值为 1。继续使用优化 图 4 进化过程 Fig. 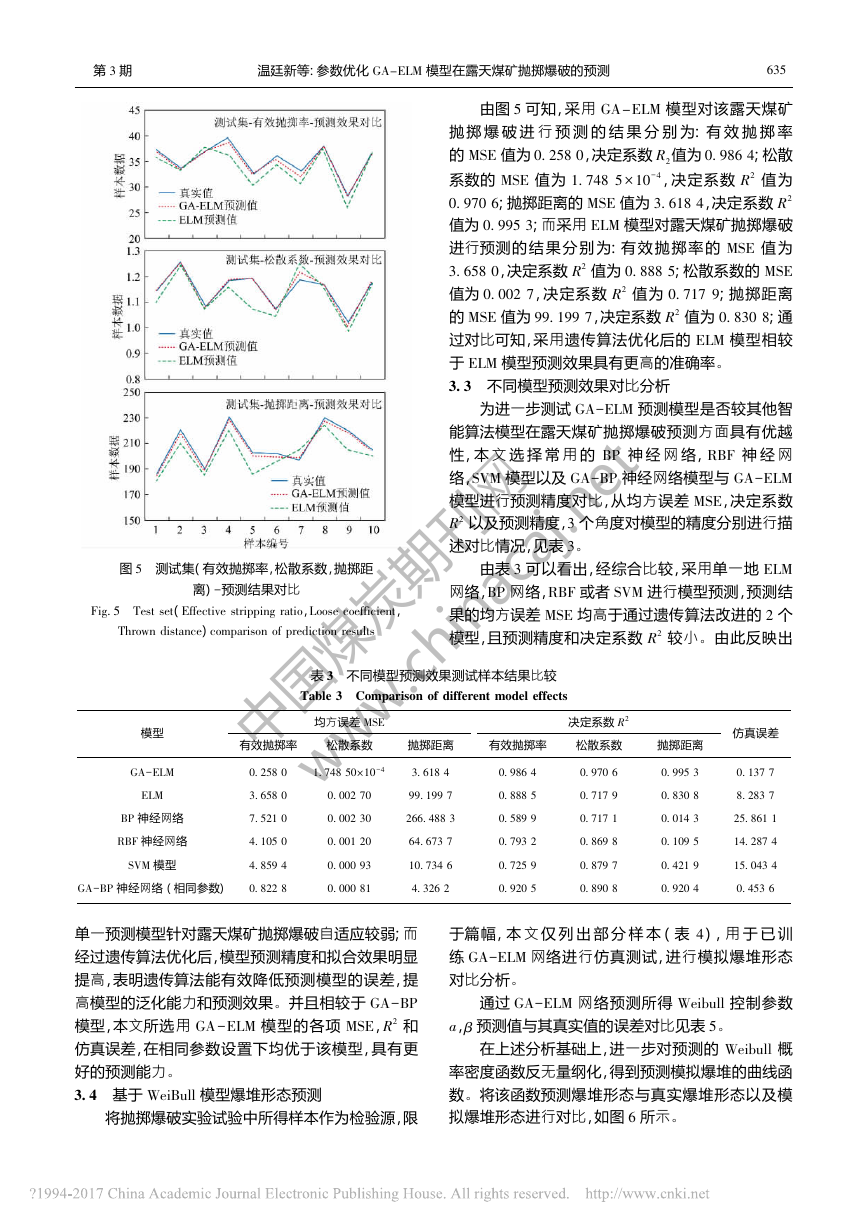4 Evolutionary process 后的 GA－ELM 模型对测试样本进行仿真预测，并与 未经遗传算法优化的 ELM 模型进行比较，测试样本 预测结果如图 5 所示。 中国煤炭期刊网 www.chinacaj.net
    第 3 期 温廷新等:参数优化 GA－ELM 模型在露天煤矿抛掷爆破的预测 536 由图 5 可知，采用 GA －ELM 模型对该露天煤矿 抛 掷 爆 破 进 行 预 测 的 结 果 分 别 为: 有 效 抛 掷 率 的 MSE 值为 0. 258 0，决定系数 Ｒ2 值为 0. 986 4;松散 系数的 MSE 值为 1. 748 5 × 10 －4，决定系数 Ｒ2 值为 0. 970 6;抛掷距离的 MSE 值为 3. 618 4，决定系数 Ｒ2 值为 0. 995 3;而采用 ELM 模型对露天煤矿抛掷爆破 进行预测 的 结 果 分 别 为: 有 效 抛 掷 率 的 MSE 值 为 3. 658 0，决定系数 Ｒ2 值为 0. 888 5;松散系数的 MSE 值为 0. 002 7，决定系数 Ｒ2 值为 0. 717 9;抛掷距离 的 MSE 值为 99. 199 7，决定系数 Ｒ2 值为 0. 830 8;通 过对比可知，采用遗传算法优化后的 ELM 模型相较 于 ELM 模型预测效果具有更高的准确率。 3. 3 不同模型预测效果对比分析 为进一步测试 GA－ELM 预测模型是否较其他智 能算法模型在露天煤矿抛掷爆破预测方面具有优越 性，本 文 选 择 常 用 的 BP 神 经 网 络，ＲBF 神 经 网 络，SVM 模型以及 GA－BP 神经网络模型与 GA－ELM 模型进行预测精度对比，从均方误差 MSE，决定系数 Ｒ2 以及预测精度，3 个角度对模型的精度分别进行描 述对比情况，见表 3。 由表 3 可以看出，经综合比较，采用单一地 ELM 网络，BP 网络，ＲBF 或者 SVM 进行模型预测，预测结 果的均方误差 MSE 均高于通过遗传算法改进的 2 个 模型，且预测精度和决定系数 Ｒ2 较小。由此反映出 图 5 测试集( 有效抛掷率，松散系数，抛掷距 离) －预测结果对比 Fig. 5 Test set( Effective stripping ratio，Loose coefficient， Thrown distance) comparison of prediction results 表 3 不同模型预测效果测试样本结果比较 Table 3 Comparison of different model effects 均方误差 MSE 有效抛掷率 松散系数 抛掷距离 有效抛掷率 决定系数 Ｒ2 松散系数 抛掷距离 仿真误差 0. 258 0 1. 748 50×10 －4 3. 618 4 0. 986 4 0. 970 6 0. 995 3 0. 137 7 3. 658 0 0. 002 70 99. 199 7 0. 888 5 0. 717 9 0. 830 8 8. 283 7 7. 521 0 0. 002 30 266. 488 3 0. 589 9 0. 717 1 0. 014 3 25. 861 1 4. 105 0 0. 001 20 64. 673 7 0. 793 2 0. 869 8 0. 109 5 14. 287 4 4. 859 4 0. 000 93 10. 734 6 0. 725 9 0. 879 7 0. 421 9 15. 043 4 模型 GA－ELM ELM BP 神经网络 ＲBF 神经网络 SVM 模型 GA－BP 神经网络 ( 相同参数) 0. 822 8 0. 000 81 4. 326 2 0. 920 5 0. 890 8 0. 920 4 0. 453 6 单一预测模型针对露天煤矿抛掷爆破自适应较弱;而 经过遗传算法优化后，模型预测精度和拟合效果明显 提高，表明遗传算法能有效降低预测模型的误差，提 高模型的泛化能力和预测效果。并且相较于 GA－BP 模型，本文所选用 GA －ELM 模型的各项 MSE，Ｒ2 和 仿真误差，在相同参数设置下均优于该模型，具有更 好的预测能力。 3. 4 基于 WeiBull 模型爆堆形态预测 将抛掷爆破实验试验中所得样本作为检验源，限 于篇幅，本 文 仅 列 出 部 分 样 本 ( 表 4 ) ，用 于 已 训 练 GA－ELM 网络进行仿真测试，进行模拟爆堆形态 对比分析。 通过 GA－ELM 网络预测所得 Weibull 控制参数 ɑ，β 预测值与其真实值的误差对比见表 5。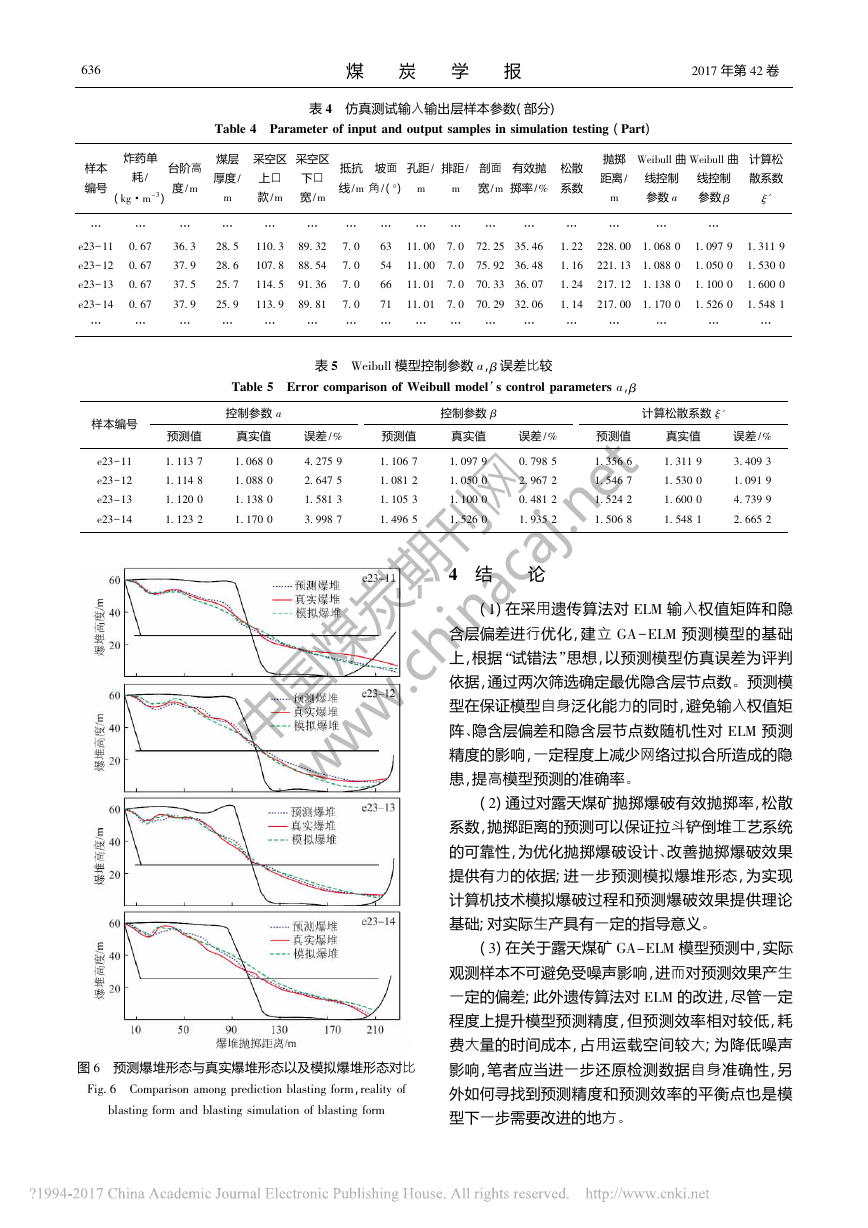 在上述分析基础上，进一步对预测的 Weibull 概 率密度函数反无量纲化，得到预测模拟爆堆的曲线函 数。将该函数预测爆堆形态与真实爆堆形态以及模 拟爆堆形态进行对比，如图 6 所示。 中国煤炭期刊网 www.chinacaj.net
    636 煤 炭 学 报 2017 年第 42 卷 表 4 仿真测试输入输出层样本参数( 部分) Table 4 Parameter of input and output samples in simulation testing ( Part) 样本 编号 炸药单 耗 / (kg·m－3 ) 台阶高 度 / m … e23－11 e23－12 … 0. 67 0. 67 e23－13 0. 67 e23－14 0. 67 … … … 36. 3 37. 9 37. 5 37. 9 … 煤层 采空区 采空区 厚度 / 上口 下口 m … 款 / m 宽 / m … … 28. 5 110. 3 89. 32 28. 6 107. 8 88. 54 25. 7 114. 5 91. 36 25. 9 113. 9 89. 81 … … … 抛掷 距离 / Weibull 曲 线控制 参数 ɑ Weibull 曲 线控制 参数 β 计算松 散系数 ξ' m … 抵抗 坡面 孔距 / 排距 / 剖面 有效抛 松散 线 / m 角 / (°) m m 宽 / m 掷率 / % 系数 … 7. 0 7. 0 7. 0 7. 0 … … 63 54 66 71 … … … … … … … … 11. 00 7. 0 72. 25 35. 46 1. 22 228. 00 1. 068 0 1. 097 9 1. 311 9 11. 00 7. 0 75. 92 36. 48 1. 16 221. 13 1. 088 0 1. 050 0 1. 530 0 11. 01 7. 0 70. 33 36. 07 1. 24 217. 12 1. 138 0 1. 100 0 1. 600 0 11. 01 7. 0 70. 29 32. 06 1. 14 217. 00 1. 170 0 1. 526 0 1. 548 1 … … … … … … … … … 表 5 Weibull 模型控制参数 ɑ， β 误差比较 Table 5 Error comparison of Weibull model’s control parameters ɑ， β 控制参数 ɑ 控制参数 β 计算松散系数 ξ' 预测值 真实值 1. 113 7 1. 114 8 1. 120 0 1. 123 2 1. 068 0 1. 088 0 1. 138 0 1. 170 0 误差 / % 4. 275 9 2. 647 5 1. 581 3 3. 998 7 预测值 真实值 1. 106 7 1. 081 2 1. 105 3 1. 496 5 1. 097 9 1. 050 0 1. 100 0 1. 526 0 误差 / % 0. 798 5 2. 967 2 0. 481 2 1. 935 2 预测值 真实值 1. 356 6 1. 546 7 1. 524 2 1. 506 8 1. 311 9 1. 530 0 1. 600 0 1. 548 1 误差 / % 3. 409 3 1. 091 9 4. 739 9 2. 665 2 样本编号 e23－11 e23－12 e23－13 e23－14 4 结 论 (1) 在采用遗传算法对 ELM 输入权值矩阵和隐 含层偏差进行优化，建立 GA －ELM 预测模型的基础 上，根据“试错法”思想，以预测模型仿真误差为评判 依据，通过两次筛选确定最优隐含层节点数。预测模 型在保证模型自身泛化能力的同时，避免输入权值矩 阵、隐含层偏差和隐含层节点数随机性对 ELM 预测 精度的影响，一定程度上减少网络过拟合所造成的隐 患，提高模型预测的准确率。 (2) 通过对露天煤矿抛掷爆破有效抛掷率，松散 系数，抛掷距离的预测可以保证拉斗铲倒堆工艺系统 的可靠性，为优化抛掷爆破设计、改善抛掷爆破效果 提供有力的依据;进一步预测模拟爆堆形态，为实现 计算机技术模拟爆破过程和预测爆破效果提供理论 基础;对实际生产具有一定的指导意义。 (3) 在关于露天煤矿 GA－ELM 模型预测中，实际 观测样本不可避免受噪声影响，进而对预测效果产生 一定的偏差;此外遗传算法对 ELM 的改进，尽管一定 程度上提升模型预测精度，但预测效率相对较低，耗 费大量的时间成本，占用运载空间较大;为降低噪声 影响，笔者应当进一步还原检测数据自身准确性，另 外如何寻找到预测精度和预测效率的平衡点也是模 型下一步需要改进的地方。 图 6 预测爆堆形态与真实爆堆形态以及模拟爆堆形态对比 Fig. 6 Comparison among prediction blasting form，reality of blasting form and blasting simulation of blasting form 中国煤炭期刊网 www.chinacaj.net
    第 3 期 温廷新等:参数优化 GA－ELM 模型在露天煤矿抛掷爆破的预测 736 参考文献( Ｒeferences) : ［1］ 李克民，张幼蒂，傅洪贤．露天煤矿抛掷爆破参数分析［J］． 采矿 与安全工程学报，2006，23(4) :423－426． Li Kemin，Zhang Youdi，Fu Hongxian． Analysis of casting blast pa- rameters in surface coal mines［J］．Journal of Mining ＆ Safety Engi- neering，2006，23(4) :423－426． ［2］ 周伟，才庆祥，李克民． 露天煤矿抛掷爆破有效抛掷率预测模型 ［J］．采矿安全与工程学报，2011，28(4) :614－617． Zhou Wei，Cai Qingxiang，Li Kemin． Prediction model of effective stripping ratio of casting blast in open pit［J］． Journal of Mining ＆ Safety Engineering，2011，28(4) :614－617． ［3］ 李祥龙，刘殿书，何丽华，等．露天煤矿的台阶高度对抛掷率的影 响［J］．爆炸与冲击，2012，32(2) :211－215． Li Xianglong，Liu Dianshu，He Lihua，et of bench height of an open-pit coal mine on cast percentage［J］．Explo- sion and Shock Waves，2013，32(2) :211－215． al． Influences ［4］ 马力，李克明，丁小华，等．抛掷爆破岩体炮制距离影响因素研究 ［J］．工程爆破，2013，19(1－2) :50－53． Ma Li，Li Keming，Ding Xiaohua，et al．Study on the influencing fac- tors on casting distance of rock by casting blast［J］． Engineering Blasting，2013，19(1－2) :50－53． ［5］ 孙文希，刘希亮，王洪斌，等． 基于 MIV 的抛掷爆破影响因子权 重分析［J］．中国矿业大学学报，2012，41(6) :993－998． Sun Wenxi，Liu Xiliang，Wang Hongbin，et al．Weight analysis of cast blasting effective factors based on MIV method［J］．Journal of China University of Mining ＆ Technology，2012，41(6) :993－998． ［6］ 刘希亮，赵学胜，陆锋，等． 基于 GA － SVM 的露天煤矿抛掷爆破 抛掷率预测［J］．煤炭学报，2012，37(12) :1999－2005． Liu Xiliang，Zhao Xuesheng，Lu Feng，et al．A GA－SVM based model for throwing rate prediction in the open-pit cast blasting［J］． Journal of China Coal Society，2012，37(12) :1999－2005． 对民房破坏的预测分析［J］．中国安全生产技术，2015，11( 8) : 119－124． Wen Tingxin，Zhu Chengwei，Kong Xiangbo． Predicting analysis on damage to residential house by blasting vibration in open pit mining based on PCA－ELM model［J］．Journal of Safety Science and Technology，2015，11(8) :119－124． ［12］ 韩亮，刘殿书，李洪江，等．基于 Weibull 模型的高台阶抛掷爆破 爆堆形态 BP 神 经 网 络 预 测［J］． 煤 炭 学 报，2013，38 ( 11 ) : 1947－1952． Han Liang，Liu Dianshu，Li Hongjiang，et al． BP neural network forecast of blasting muck pile form of high bench cast blasting based on Weibull model［J］． Journal of China Coal Society，2013， 38(11) :1947－1952． ［13］ Huang Guangbin，Zhu Qinyu，Siew C K．Extreme learning machine: Theory and application［J］．Neurocomputing，2006，70( 1 /3) :489－ 501． ［14］ Huang Guangbin，Zhu Qinyu，Siew C K．Ｒeal-time learning capabil- ity of neural networks［J］．Neurocomputing，2006，70:863－878． ［15］ Lan Yuan，Soh Y C，Huang Guangbin． Ensemble of online sequen- tial extreme learning machine［J］． Neurocomputing，2009，72 ( 13 / 15) :3391－3395． ［16］ Huang Guangbin，Ding Xiaojian，Zhou Hongming． Optimiza- tion method based extreme learning machine for classification ［J］．Neurocomputing，2010，74(1 /3) :155－163． ［17］ 张玲，张钹．遗传算法机理的研究［J］． 软件学报，2000，11( 7) : 945－952． Zhang Ling，Zhang Bo．Ｒesearch on the mechanism of genetic algo- rithms［J］．Journal of Software，2000，11(7) :945－952． ［18］ 戴晓辉，李敏强，寇纪淞．遗传算法理论研究综述［J］．控制与决 策，2000，15(3) :263－268． Dai Xiaohui，Li Minqiang，Kou Jisong．Survey on the theory of ge- netic algorithms［J］． Control and Decision，2001，15 ( 3 ) : 263 － ［7］ 孙文希，刘希亮，谭正龙，等．基于抛掷爆破预测的 BP 神经网络 268． 参数优化方法［J］．煤炭学报，2012，37(1) :59－64． Sun Wenxi，Liu Xiliang，Tan Zhenglong，et al．Parameter optimization of BP-neural network based on the forecast of cast blasting［J］．Jour- nal of China Coal Society，2012，37(1) :59－64． ［8］ 刘干，李克民，肖双双，等． 露天煤矿抛掷爆破有效抛掷率预测 ［J］．金属矿山，2014(4) :65－69． Liu Gan，Li Kemin，Xiao Shuangshuang，et al． Prediction of effective stripping ratio of casting blast in surface coal mines［J］．Metal Mine， 2014(4) :65－69． ［9］ 周志坚，毛宗源． 一种最优模糊神经网络控制器［J］． 控制与决 策，2000，15(3) :358－360． Zhou Zhijian，Mao Zongyuan． An optimal fuzzy neural network con- troller［J］．Control and Decision，2000，15(3) :358－360． ［10］ 温廷新，戚磊，邵良杉． 露天采矿爆破振动特征参量的 Logistic- ELM 预测［J］．计算机工程与设计，2015，36(10) :2791－2795． Wen Tingxin，Qi Lei，Shao Liangshan． Prediction blasting vibra- tion characteristic parameters in open-pitmining based on Logistic- ELM［J］．Computer Engineering and Design，2015，36(10) :2791－ 2795． ［11］ 温廷新，朱成伟，孔祥博．基于 PCA－ELM 模型的露采爆破振动 ［19］ 玄光男，程润伟，于歆杰，等． 遗传算法与工程优化［M］． 北京: 清华大学出版社，2004:24－30． Xuan Guangnan，Cheng Ｒunwei，Yu Xinjie，et al．Genetic algorithms and engineering optimization ［M］． Beijing: Tsinghua University Press，2004:24－30． ［20］ 丁小华，李克民，狐为民，等．基于非线性理论的抛掷爆破爆堆 形态预测［J］．中国矿业大学学报，2012，41(5) :764－769． Ding Xiaohua，Li Kemin，Hu Weimin，et al． Prediction of opti- mum muck pile casting shape during blasting: A nonlinear theory ［J］． Journal of China University of Mining ＆ Technology，2012， 41(5) :764－769． ［21］ 傅洪贤，李克民．露天煤矿高台阶抛掷爆破参数分析［J］． 煤炭 学报，2006，31(4) :442－445． Fu Hongxian，Li Kemin．Analysis of high bench cast blasting param- eters in surface coal mines［J］． Journal of China Coal Society， 2006，31(4) :442－445． ［22］ 缪伟，赵庆，王斯日古楞．哈尔乌素露天煤矿抛掷爆破参数的确 定［J］．煤矿安全，2013(11) :211－213． Miao Wei，Zhao Qing，Wang Siriguleng． Determination of casting blast parameters for Haerwusu open-pit coal mine［J］． Safety in 中国煤炭期刊网 www.chinacaj.net
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料