第 37 卷 第 19 期 Vol.37 No.19 ·图形图像处理· 计 算 机 工 程 Computer Engineering 文章编号：1000—3428(2011)19—0215—03 2011 年 10 月 October 2011 文献标识码：A 中图分类号：TP393 基于压缩感知的图像快速重建方法 侯金曼 1，何 宁 2，吕 科 1 (1. 中国科学院研究生院计算与通信工程学院，北京 100049；2. 北京联合大学信息学院，北京 100101) 摘 要：基于多种稀疏变换基和观测矩阵的组合，采用正交匹配追踪算法对图像进行重建。在分析各种组合重建效果的基础上，提出一种 图像快速重建方法，对图像进行一级小波分解，提取出近似分量子图像，运用压缩感知技术对其进行恢复，综合细节分量和恢复出的近似 分量进行小波逆变换，得到重建图像。实验结果表明，该方法在相同的观测值条件下，能减少算法运行时间，提高重建图像质量。 关键词：压缩感知；稀疏表示；小波分解；图像重建；正交匹配追踪 Image Fast Reconstruction Method Based on Compressive Sensing HOU Jin-man1, HE Ning2, LV Ke1 (1. College of Computing & Communication Engineering, Graduate University of Chinese Academy of Sciences, Beijing 100049, China; 2. College of Information, Beijing Union University, Beijing 100101, China) 【Abstract】Orthogonal Matching Pursuit(OMP) algorithm is used to reconstruct images based on the combinations of several common sparse transform bases and measurement matrices. This paper analyzes and compares the reconstruction results with above various combinations. And on this basis, a fast image reconstruction method is proposed. A multi-scale wavelet decomposition is used to extract the approximate coefficients from the image. It uses compressed sensing method to recover these approximate coefficients, and the reconstructed images are obtained with inverse wavelet transform based on detail coefficients and recovered approximate coefficients. Experimental results show that with the same number of measurement values, the run time of this method and the quality of the reconstructive images have great improvements. 【Key words】compressive sensing; sparse representation; wavelet decomposition; image reconstruction; Orthogonal Matching Pursuit(OMP) DOI: 10.3969/j.issn.1000-3428.2011.19.071 1 概述 在传统采样中，依据 Nyquist 采样定理，采样频率不能 低于信号最高频率的 2 倍，当信号很长时无疑会增加采样量， 给传输和存储带来巨大挑战。传统采样理论对信息获取、存 储及传输等有很大限制。 文献[1-2]提出一种新的信息获取理论，即压缩感知[1-2]， 其思想主要是：通过远低于 Nyquist 采样率的方式对稀疏的 或可压缩的信号进行采样，同时能以高概率精确地恢复出原 信号。该理论在信息论、图像处理、医疗成像、模式识别等 很多领域受到高度关注。 本文采用经典的 5 种稀疏变换基和 5 种观测矩阵的不同 组合对多幅图像进行重建实验，分析比较了各种组合的重建 效果，并提出一种新的图像快速重建方法。 2 压缩感知 2.1 压缩感知的主要理论框架 压缩感知中主要涉及以下问题：(1)信息的稀疏表示问 题，即如何选择合适的基底使所关注的信号在该基底下表现 出最强的稀疏性。(2)采样方式的选择问题，即如何选择合适 的采样机制以有效利用信息本质上的稀疏性使得在较少的测 量下完全恢复信号。(3)稀疏信号的完全重建问题，即以什么 样的算法完全重建不完全采样下的信号。 在第(1)个问题中，一个长度为 N 的一维离散时间信号 x ，可以表示为一组正交基 iΨ 的线性组合，把向量集 { iΨ 作为列向量形成 N N× 的基矩阵 Ψ ，则信号 x 可以表 { 示成如下形式： }N i= 1 }N i= 1 ,M ，记观测向量 = = x = ∑ i θ Ψ 或 i N i= 1 =θ Ψ x (1) T 其中，θ 是投影系数，如果 θ 只有很少的大系数，则说信号 x 是可压缩的。常用的稀疏变换基有傅里叶变换基、小波基、 离散余弦变换(Discrete Cosine Transform, DCT)变换基等。 观测过程是利用 M N× 的观测矩阵 Φ 的 M 个行向量对 1, 投影系数 θ 进行投影，得到 M 个观测值 2, =< ，则： θ,Φ =y y y , 1 )M jy > , , y , 2 j = ( j T = y Φθ ΦΨ x Ax (2) 若 Φ 满 足 一 致 不 确 定 性 原 则 (Uniform Uncertainty Principle, UUP)或一定阶数的约束等距性(Restricted Isometry Property, RIP)条件，则由少量观测值以高精确重构原始信 号[3]。同时给出 2 种满足 RIP 的观测矩阵：高斯随机观测矩 阵和 Bernoulli 随机观测矩阵[3]。 其他常用的满足 RIP 条件的观测矩阵还有二值随机矩 阵、局部哈达玛矩阵、非相关测量矩阵[4]以及非常稀疏随机 投影矩阵等。 针对信号的重建问题，在信号 x 稀疏或可压缩的前提下， 可将该问题转化为求解最小 0L 范数问题[5]： 基金项目：国家自然科学基金资助项目(61070120)；国家“973”计 划基金资助项目(2010CB731804-1)；公益性行业(气象)科研专项基金 资助项目(2060302-21) 作者简介：侯金曼(1985－)，女，硕士研究生，主研方向：数字图像 处理；何 宁，副教授、博士；吕 科，教授、博士 收稿日期：2011-04-22 E-mail：houjm09@gmail.com 

216 计 算 机 工 程 2011 年 10 月 5 日 0 Ψ x T Ax ΦΨ x T min y (3) s.t. 但是，文献[6]指出该问题是 NP 难问题，可以将式(3)转 = = 化为最小 1L 范数问题等价求解： 1 y = = Ψ x T Ax ΦΨ x T min (4) s.t. 目前常用的恢复算法有内点法、梯度投影法、正交匹配 追踪(Orthogonal Matching Pursuit, OMP)算法[7]、迭代阈值法 以及各种改进算法等。 2.2 正交匹配追踪算法 文献[7]提出的一种正交匹配追踪算法属于贪婪迭代方 法，其描述如下： 输入 (1) M N× 维的观测矩阵 Φ ； (2) M 维的观测向量 y ； (3)信号 s 的稀疏度 K 。 输出 (1)原始信号的近似估计 ˆs ； (2)索引集合 KΛ ； (3)向量 y 的 M 维近似向量 Kα ； (4) M 维的冗余向量 K y α 。 r 算法具体步骤如下： (1)初始化冗余向量 0 =r = − K y ，索引集合 0 φ=Λ ，选择的列 向量组成的矩阵 0 φ=Φ ，迭代计数 1 t = ； (2)找到观测矩阵的列向量与冗余向量的内积最大的索 r t 1 − , ϕ j > ； 引位置 tλ，即使其满足 { } tλ− 1 Λ t ∪ j N arg max < = λ t Φ Φ ； ， = t x t , 1,2, = ] t ϕ tλ -1 arg min = [ = Λ t (3)记 (4)利用最小二乘法计算 (5)计算新的近似和冗余向量： t (6) (7)原信号 s 的近似估计 ˆs 在索引位置 KΛ 处的项非零，且 y ； − 2 =α Φ x ， t r = − t= + ，如果 t K< ，则返回步骤(2)； y α ； Φ x t 1 t x t t t (4)Coiflets 小波。Coiflet 小波具有 Coif 系 列。Coiflet 的小波函数 ( )tψ 的 2N 阶矩为 0，尺度函数 ( )tφ 的 2 1N − 阶矩为 0。 1,2,3,4,5) N N = ( (5)Symlets 小波。Symlets 小波函数是近似对称的小波函 数，它是对 db 函数的一种改进。Symlets 小波系通常表示为 Sym ( N N = 。 实验采用的观测矩阵描述如下： (1)高斯随机矩阵：矩阵中每个元素都独立地服从均值为 2,3, ,8) 0、方差为 的正态分布。 1 M (2)Bernoulli 随机矩阵：矩阵中每个元素独立服从对称 Bernoulli 分布。 (3)非相关测量矩阵：从 N 阶正交矩阵中均匀随机抽取 M 行作为行向量组成新矩阵，并单位化新矩阵的列向量。 (4)局部哈达玛矩阵：从 N 阶哈达玛矩阵中随机抽取 M 行。 (5)非常稀疏投影矩阵：矩阵中每个元素独立服从如下 分布： s 1 0 − − X 1 s ⎤ ⎥ ⎥ ⎥ ⎦ 1 s 2 s ~ 1 s 2 s >> 时，称 X 服从非常稀疏投影分布，本文取 3 = 。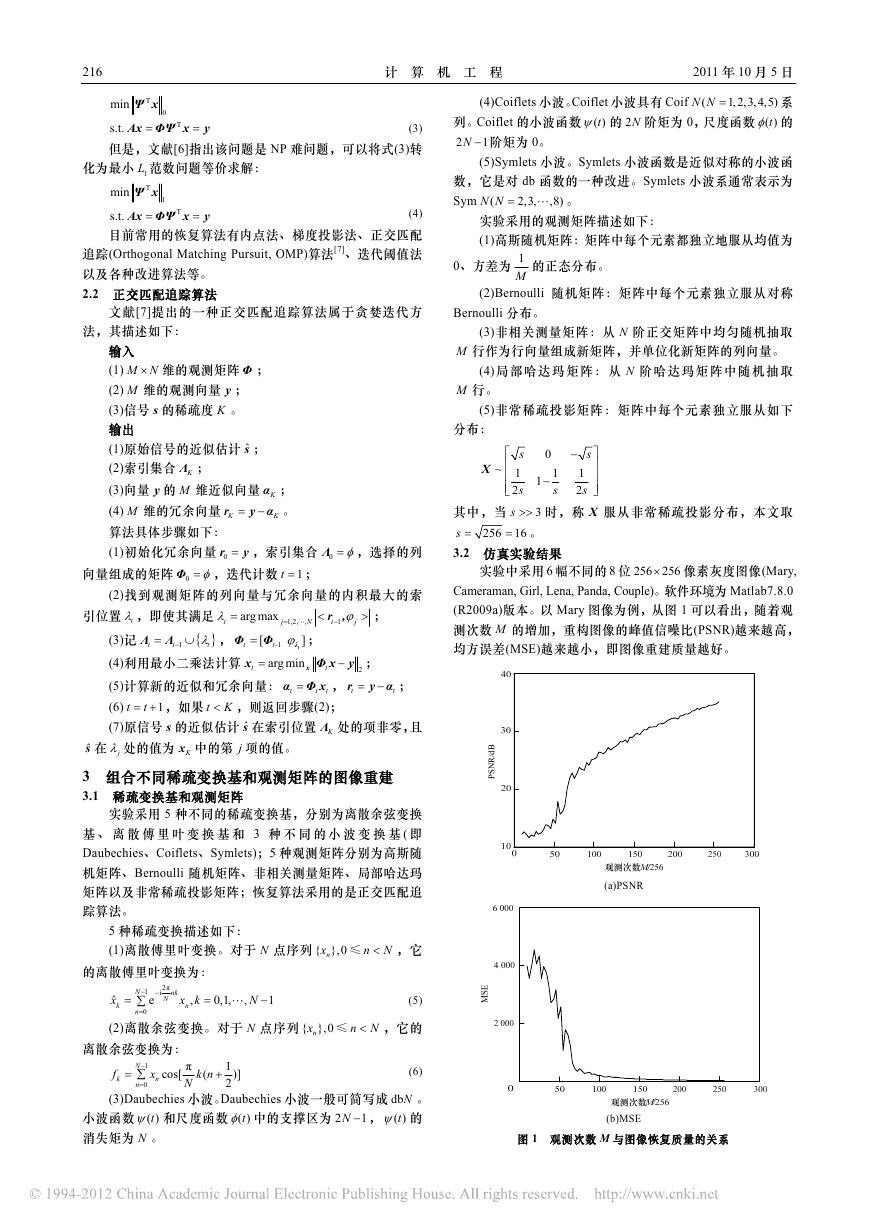 16 ⎡ ⎢ ⎢ ⎢ ⎣ 其中，当 s = 256 3.2 仿真实验结果 实验中采用 6 幅不同的 8 位 256 256 × 像素灰度图像(Mary, Cameraman, Girl, Lena, Panda, Couple)。软件环境为 Matlab7.8.0 (R2009a)版本。以 Mary 图像为例，从图 1 可以看出，随着观 测次数 M 的增加，重构图像的峰值信噪比(PSNR)越来越高， 均方误差(MSE)越来越小，即图像重建质量越好。 B d / R N S P ˆs 在 jλ 处的值为 Kx 中的第 j 项的值。 3 组合不同稀疏变换基和观测矩阵的图像重建 3.1 稀疏变换基和观测矩阵 实验采用 5 种不同的稀疏变换基，分别为离散余弦变换 基 、 离 散 傅 里 叶 变 换 基 和 3 种 不 同 的 小 波 变 换 基 ( 即 Daubechies、Coiflets、Symlets)；5 种观测矩阵分别为高斯随 机矩阵、Bernoulli 随机矩阵、非相关测量矩阵、局部哈达玛 矩阵以及非常稀疏投影矩阵；恢复算法采用的是正交匹配追 踪算法。 5 种稀疏变换描述如下： (1)离散傅里叶变换。对于 N 点序列 { },0nx n N<≤ ，它 的离散傅里叶变换为： (a)PSNR − i 2π N nk N 1 − ∑ n 0 = e = x k , n ˆ x k (2)离散余弦变换。对于 N 点序列 { },0nx 0,1, N = − 1 , (5) n N<≤ ，它的 离散余弦变换为： π cos[ N N 1 − ∑ n 0 = x n = 1 2 + )] k n ( (6) f k (3)Daubechies 小波。Daubechies 小波一般可简写成 dbN 。 1N − ， ( )tψ 的 小波函数 ( )tψ 和尺度函数 ( )tφ 中的支撑区为 2 消失矩为 N 。 (b)MSE 图 1 观测次数 M 与图像恢复质量的关系 

第 37 卷 第 19 期 217 侯金曼，何 宁，吕 科：基于压缩感知的图像快速重建方法 可以看出，当 M 取大于 80 以上的数目时，2 条曲线的 变化趋势均变得比较缓和，即图像的恢复质量才能比较稳定。 当小于这个值时，2 条曲线均比较陡峭，变化趋势较大，基 本不能恢复原图像。这说明保证图像的重构质量，观测次数 M 不能任意取值。 在图 2 中，横坐标分为 5 个小区间，每个小区间对应一 个稀疏变换基，分别为离散余弦变换基、Symlets 小波变换基、 Daubechies 小波变换基、离散傅里叶变换基和 Coiflets 小波 变换基，在每个小区间内部的 5 个取值分别对应 5 种不同的 观测矩阵，顺序依次为高斯随机矩阵、Bernoulli 随机矩阵、 非相关测量矩阵、局部哈达玛矩阵以及非常稀疏投影矩阵， 这样就构成了 25 种不同的稀疏变换基和观测矩阵的组合。 38 36 34 32 30 28 26 24 22 20 Cameraman图像 Mary图像 Girl图像 Panda图像 Couple图像 Lena图像 0 5 10 15 20 25种变换基和观测矩阵的组合 图 2 不同组合的图像恢复质量比较 25 可以看出，在相同的组合条件下，对于不同的图像，重 建质量也不一样，而对于同一幅图像，选用不同的变换基与 观测矩阵，其重建质量也不相同。在本次实验中，对于不同 的 6 幅图像分别采用 5 5× 种不同的变换基和观测矩阵的组合 对其进行重建，重建效果曲线的分布趋势基本相同。仔细分 析每条曲线的走势可知，当观测矩阵为非相关测量矩阵和局 部哈达玛矩阵，变换基取 3 种不同的小波基时，图像的重建 质量比较高。 4 改进的图像快速重建方法 4.1 方法描述 在现有的实验基础上，图像的重建时间还是比较长的， 因此，需要减少图像的重建时间。 对二维原始图像进行一级小波变换后，原始图像被分解 成 4 个子图像，每个子图像包含了原始图像中不同的频率成 分。左上角子图包含了图像的近似分量，即图像的主要特征； 右上角子图像包含了图像的垂直分量；左下角子图像包含了 图像的水平分量；右下角子图像包含了图像的对角分量。经 过小波变换，每个子图像长宽尺寸也降低到原来的一半，即 分辨率降低到原来的 1/4。 借鉴以上思想，本文提出一种新的图像快速重建方法， 具体步骤如下： (1)对原始图像进行一次一级小波变换，提取出图像的近 似分量子图像； (2)对近似分量子图像运用压缩感知技术进行恢复； (3)综合细节分量和恢复出的近似分量进行相应的小波 逆变换，得到重建图像。 4.2 实验结果 本实验中一级小波变换采用 Daubechies 小波 (db4) ，稀 疏变换基采用 Coiflets 小波基，观测矩阵选用高斯随机矩阵， 观测个数取 M =46 080，重建效果对比如图 3 和表 1 所示， 其中，图 3 和表 1 中的 A 方法表示直接对整幅图像进行基于 压缩感知重建的方法；B 方法为本文方法。 (a)A 方法重建的 Mary 图像 (b)B 方法重建的 Mary 图像 (c)A 方法重建的 Cameraman 图像 (d)B 方法重建的 Cameraman 图像 (e)A 方法重建的 Girl 图像 (f)B 方法重建的 Girl 图像 (g)A 方法重建的 Lena 图像 (h)B 方法重建的 Lena 图像 (i)A 方法重建的 Panda 图像 (j)B 方法重建的 Panda 图像 (k)A 方法重建的 Couple 图像 (l)B 方法重建的 Couple 图像 图 3 A 方法和 B 方法重建图像的对比效果 (下转第 226 页) 

226 计 算 机 工 程 2011 年 10 月 5 日 核，结合本文设计的 LAN83C185 的物理层协议(PHY)，在 MicroBlaze 做好封包解包软件处理，实现相应的以太网协议， 方便本文设计的板卡和主站的远程数据交互。 根据文献[5]协议要求，本节给出一个 UDP/IP 协议的实 现，在软件结构体中初始化各首部数据，并将采集到的数据 封装成帧，主站通过 Wireshark 网络分析工具解包验证如 图 6(a)所示。 手成功，然后建立数据通信，图 6(b)给出了本地串口的信息 回显，结果表明通信正确可靠。 4 结束语 本文介绍了一种基于 SOPC 的高精度三相电参数采集和 传输系统。从软硬件设计上，对数据采集芯片本身的特性、 电源结构、数据采集 IP 核设计、基于 UDP/IP 的远程数据传 输、MPMC 内存控制器及 MicroBlaze 软核处理器做了重点分 析。在自行设计出的硬件平台上完成各模块代码的编写并实 现，各指标测试通过且运行稳定。对于电网中诸多采集器的 以太网组网管理存在时钟同步等技术难点[6]，在后续研究中 将建立庞大可靠的以太网现场校表仪系统，为国家智能电网 建设提供技术支持。 (a)以太网测试结果 (b)串口测试结果 图 6 通信验证结果界面 参考文献 [1] 沈兰荪. 高速数据采集系统的原理与应用[M]. 北京: 人民邮电 出版社, 1995. [2] Sun Hao, Yuan Huimei, Lu Sime. A Design of Three-phase Digital Watt-hour Power Meter on SOPC Platform[C]//Proc. of Interna- tional Conference on Information Technology and Computer Science. [S. l.]: IEEE Press, 2009. [3] Analog Devices, Inc.. 250 kSPS, 6-Channel, Simultaneous Samp- ling, Bipolar 16-/14-/12-Bit ADC[EB/OL]. (2006-05-11). http:// www.spectrum-instrumentation.com. [4] Xilinx, Inc.. Multi-port Memory Controller[EB/OL]. (2009-11-12). http://www.xilinx.com/support/documentation/m pmc.pdf. [5] Stevens W R. TCP/IP 详解(卷 1: 协议)[M]. 胡谷雨, 昊礼发, 译. 发送端(本采集卡)发送地址解析协议(Address Resolution Protocol, ARP)广播帧，寻找 MAC 地址为 00-0F-FE-DB-7C-EE 的主机，希望和其建立通信，该主机(和本采集卡共用 HUB 的主机)收到 ARP 广播帧后，发回其 IP 地址 59.71.73.210 和 编辑 陆燕菲 MAC 地址 00-0F-FE-DB-7C-EE，并将 option 置位成 2 表示握 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (上接第 217 页) [6] 何 伟, 林英撑, 张 玲. 基于 NIOSⅡ的时钟同步数据采集系 统[J]. 计算机工程, 2009, 35(9): 243-245. 北京: 机械工业出版社, 2005. 表 1 A 和 B 方法重建图像的实验结果 参考文献 B 方法 [1] Donoho D L. Compressed Sensing[J]. IEEE Transactions on 图像 Mary A 方法 MSE 38.278 6 时间 t/s 31.492 6 PSNR/dB 时间 t/s MSE 9.538 5 18.492 3 32.301 2 PSNR/dB 35.460 9 Cameraman 30.895 7 129.663 5 27.002 6 9.960 7 41.704 0 31.929 0 Girl Lena 30.396 6 83.067 4 28.936 5 9.835 6 39.980 7 32.112 3 30.892 4 59.973 1 30.351 2 9.542 6 20.120 8 35.094 3 Panda 30.520 7 116.797 9 27.456 5 9.552 1 47.104 6 31.400 2 Couple 30.796 1 61.986 8 30.207 8 9.934 8 23.681 4 34.386 7 可以看出，在相同的观测次数下，本文方法比直接对整 幅图像应用压缩感知重建方法的运行时间有显著提高，同时 图像的重建质量均有明显改善。为了获得相同的重建质量， 本文方法所需的观测次数更少，程序运行时间也更少。 5 结束语 本文先对压缩感知的理论进行介绍，然后将其应用到二 维图像的重建上，得到质量较好的重建图像。在此基础上， 提出一种改进的快速图像重建方法，在获得相同的重建质量 前提下，该方法可以显著缩短程序运行时间，提高图像重建 的效率，该方法具有一定的应用价值。 Information Theory, 2006, 52(4): 1289-1306. [2] Candés E, Tao T. Near Optimal Signal Recovery from Random Projections: Universal Encoding Strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425. [3] Candés E, Tao T. Decoding by Linear Programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215. [4] Cand E. Compressive Sampling[EB/OL]. (2006-03-11). http:// www.users.cms.caltech.edu/Tro07-Compressive-Sampling-Lec1Va nderbilt.pdf. [5] Baraniuk R. A Lecture on Compressive Sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. [6] Chen Shaobin, Donoho D L, Saunders M A. Atomic Decomposition by Basis Pursuit[J]. SIAM Journal on Scientific Computing, 2001, 43(1): 129-159. [7] Tropp J, Gilbert A. Signal Recovery from Partial Information via IEEE Transactions on Orthogonal Matching Pursuit[J]. Information Theory, 2007, 53(12): 4655-4666. 编辑 陆燕菲