离散数学第三版课后答案.pdf-资料库

课后答案网 http://www.khdaw.com http://www.khdaw.cn 第 1 章习题解答 1．1 除（3），（4），（5），（11）外全是命题，其中，（1），（2），（8），（9），（10），（14），（15）是简单命题，（6），（7），（12），（13）是复合命题。分析首先应注意到，命题是陈述句，因而不是陈述句的句子都不是命题。本题中，（3）为疑问句，（5）为感叹句，（11）为祈使句，它们都不是陈述句，所以它们都不是命题。其次，（4）这个句子是陈述句，但它表示的判断结果是不确定。又因为（1），（2），（8），（9），（10），（14），（15）都是简单的陈述句，因而作为命题，它们都是简单命题。（6）和（7）各为由联结词“当且仅当”联结起来的复合命题，（12）是由联结词“或”联结的复合命题，而（13）是由联结词“且”联结起来的复合命题。这里的“且”为“合取”联结词。在日常生活中，合取联结词有许多表述法，例如，“虽然……，但是……”、“不仅……，而且……”、“一面……，一面……”、“……和……”、“……与……”等。但要注意，有时“和”或“与” 联结的是主语，构成简单命题。例如，（14）、（15）中的“与”与“和”是联结的主语，这两个命题均为简单命题，而不是复合命题，希望读者在遇到“和”或 “与”出现的命题时，要根据命题所陈述的含义加以区分。 1．2 （1） 2:p 是无理数，p 为真命题。（2） 5:p 能被 2 整除，p 为假命题。（6） p → 。其中， 2:p 是素数，q：三角形有三条边。由于 p 与 q 都是真 q 命题，因而 p → 为假命题。 q （7） p → ，其中，p：雪是黑色的，q：太阳从东方升起。由于 p 为假命 q 题，q 为真命题，因而 p → 为假命题。 q （8） 2000 :p 年 10 月 1 日天气晴好，今日（1999 年 2 月 13 日）我们还不知道 p 的真假，但 p 的真值是确定的（客观存在的），只是现在不知道而已。（9）p：太阳系外的星球上的生物。它的真值情况而定，是确定的。 1

课后答案网课后答案网 http://www.khdaw.com http://www.khdaw.com http://www.khdaw.cn http://www.khdaw.cn （10）p：小李在宿舍里. p 的真值则具体情况而定，是确定的。（12） q p ∨ ，其中， 4:p 是偶数， 4:q 是奇数。由于 q 是假命题，所以，q 为假命题， q p ∨ 为真命题。（13） q p ∨ ，其中， 4:p 是偶数， 4:q 是奇数，由于 q 是假命题，所以， q p ∨ 为假命题。（14） p：李明与王华是同学，真值由具体情况而定（是确定的）。（15） p：蓝色和黄色可以调配成绿色。这是真命题。分析命题的真值是唯一确定的，有些命题的真值我们立即可知，有些则不能马上知道，但它们的真值不会变化，是客观存在的。 1．3 令 p 22: =+ ,4 q 33: =+ ,6 则以下命题分别符号化为（1） p → q （2） p ¬→ q （3） p →¬ q （4） ¬→¬ p q （5） p ↔ q （6） p ¬↔ q （7） p →¬ q （8） ¬↔¬ p q 以上命题中，（1），（3），（4），（5），（8）为真命题，其余均为假命题。分析本题要求读者记住 p → 及 q p ↔ 的真值情况。 q p → 为假当且仅当 q p 为真,q 为假,而 p ↔ 为真当且仅当 p 与 q 真值相同.由于 p 与 q 都是真命题， q 在 4 个蕴含式中，只有（2） p → ，其中，p 同（1），r：明天为 3 号。 r 在这里，当 p 为真时，r 一定为假， p → 为假，当 p 为假时，无论 r 为真 r 还是为假， p → 为真。 r 2

课后答案网 http://www.khdaw.com http://www.khdaw.cn 1．5 （1） q p ∧ ，其中，p：2 是偶数，q：2 是素数。此命题为真命题。（2） q p ∧ ，其中，p：小王聪明，q：小王用功（3） q p ∧ ，其中，p：天气冷，q：老王来了（4） q p ∧ ，其中，p：他吃饭，q：他看电视（5） q p ∧ ，其中，p：天下大雨，q：他乘公共汽车上班（6） p → ，其中，p，q 的含义同（5） q （7） p → ，其中，p，q 的含义同（5） q （8） ¬↔¬ p q ，其中，p：经一事，q：长一智分析 1°在前 4 个复合命题中，都使用了合取联结词，都符号化为合取式，这正说明合取联结词在使用时是很灵活的。在符号化时，应该注意，不要将联结词部分放入简单命题中。例如，在（2）中，不能这样写简单命题：p：小王不但聪明，q：小王而且用功。在（4）中不能这样写：p：他一边吃饭， q：他一边看电视。 2° 后 4 个复合命题中，都使用了蕴含联结词，符号化为蕴含式，在这里，关键问题是要分清蕴含式的前件和后件。 p → 所表达的基本逻辑关系为，p 是 q 的充公条件，或者说 q 是 p 的必要 q 条件，这种逻辑关系在叙述上也是很灵活的。例如，“因为 p，所以 q”，“只要 p，就 q”“p 仅当 q”“只有 q 才 p”“除非 q，否则 p¬ ”“没有 q，就没有 p”等都表达了 q 是 p 的必要条件，因而都符号化为 p → 或 q ¬↔¬ p q 的蕴含式。在（5）中，q 是 p 的必要条件，因而符号化为 p → ，而在（6）（7）中， q p 成了 q 的必要条件，因而符号化为 q → 。 p 在（8）中，虽然没有出现联结词，但因两个命题的因果关系可知，应该符号化为蕴含式。 1．6 （1），（2）的真值为 0，（3），（4）的真值为 1。分析 1° （1）中公式含 3 个命题变项，因而它应该有 23 = 个赋值：000， 8 3

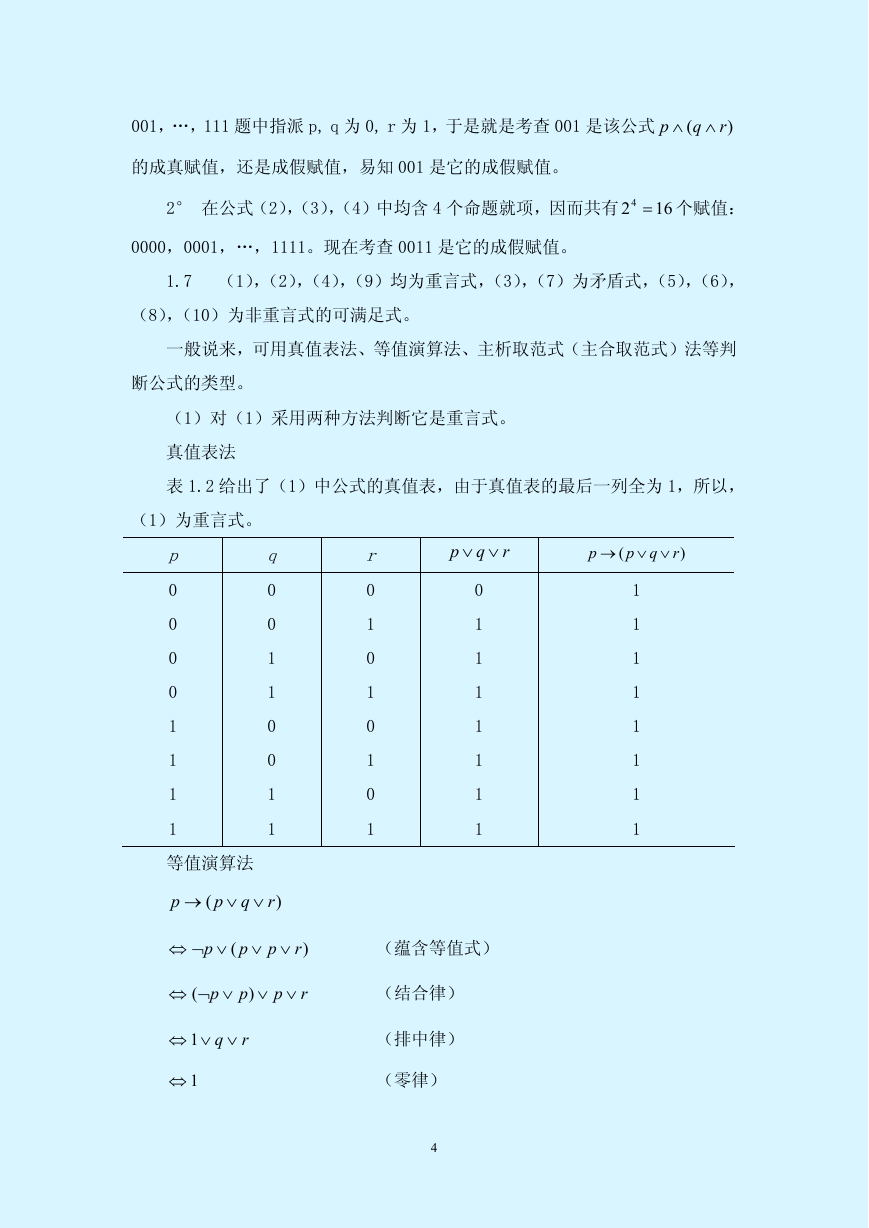
001，…，111 题中指派 p, q 为 0, r 为 1，于是就是考查 001 是该公式 p ∧ ( q ∧ r ) 的成真赋值，还是成假赋值，易知 001 是它的成假赋值。 2° 在公式（2），（3），（4）中均含 4 个命题就项，因而共有 24 = 个赋值： 16 0000，0001，…，1111。现在考查 0011 是它的成假赋值。 1.7 （1），（2），（4），（9）均为重言式，（3），（7）为矛盾式，（5），（6），（8），（10）为非重言式的可满足式。一般说来，可用真值表法、等值演算法、主析取范式（主合取范式）法等判断公式的类型。（1）对（1）采用两种方法判断它是重言式。真值表法表 1.2 给出了（1）中公式的真值表，由于真值表的最后一列全为 1，所以，（1）为重言式。 p q r rqp ∨∨ p rqp ∨∨→ ( ) 0 0 0 0 1 1 1 1 等值演算法 p ∨∨→ q ( p 0 1 0 1 0 1 0 1 0 1 1 1 1 1 1 1 0 0 1 1 0 0 1 1 r ) 1 1 1 1 1 1 1 1 ∨¬⇔ p ( p ∨∨ p r ) （蕴含等值式） ∨¬⇔ p ( p ) ∨∨ p r （结合律） q ∨∨⇔ 1 r 1⇔ （排中律）（零律） 4

由最后一步可知，（1）为重言式。（2）用等值演算法判（2）为重言式。 ( p p ¬→¬→ ) p ¬→¬∨¬⇔ p ) ( p （蕴含等值式） p ¬∨¬⇔ p p ¬∨⇔ p 1⇔ （等幂律）（蕴含等值式）（排中律）（3）用等值演算法判（3）为矛盾式 ∧→¬ q p ) ( q ∨¬¬⇔ p ( q ) ∧ q （蕴含等值式） ∧¬∨⇔ q p q ∧¬∨⇔ q p ( q ) 0∧⇔ p 0⇔ （德·摩根律）（结合律）（矛盾律）（零律）由最后一步可知，（3）为矛盾式。（5）用两种方法判（5）为非重言式的可满足式。真值表法 p 0 0 1 1 q 0 1 0 1 p¬ p →¬ q q ¬→ p ( 1 1 0 0 0 1 1 1 1 1 1 0 由表 1.3 可知（5）为非重言式的可满足式。主析取范式法 ( ¬→→→¬ ( q q p ) p ) ¬→→→¬ ( q q p ) p ) 1 1 1 0 ¬∨¬→∨⇔ q ) q ( ( p p ) 5

∨¬⇔ p ( q ) p ¬∨¬∨ q ( ) ¬∨¬∨¬∨¬⇔ q ) q p ( p p ¬∨¬⇔ q q ¬∧∨∧¬⇔ )1 1( p ( ) ∨¬∧¬⇔ q p ( ( q ) ∨¬∨ (( p p ) ¬∧ q ) ∨¬∨¬∧¬⇔ qp q p ( ) ( ∨¬∨¬∧¬⇔ qp q p ( ) ( ) ) ∨¬∧¬∨ q p ) ( ( p ¬∨ q ) q ¬∧¬∨ p ( ) ∨⇔ mmm ∨ 1 0 . 2 在（3）的主析取范式中不含全部（4 个）极小项，所以（3）为非重言式的可满足式，请读者在以上演算每一步的后面，填上所用基本的等值式。其余各式的类型，请读者自己验证。分析 o1 真值表法判断公式的类别是万能。公式 A 为重言式当且仅当 A 的真值表的最后一旬全为 1；A 为矛盾式当且仅当 A 的真值表的最后一列全为 0；A 为非重言式的可满足式当且仅当 A 的真值表最后一列至少有一个 1，又至少有一个 0。真值表法不易出错，但当命题变项较多时，真值表的行数较多。 o2 用等值演算法判断重言式与矛盾式比较方例，A 为重言式当且仅当 A 与 1 等值；A 为矛盾式当且仅当 A 与 0 等值，当 A 为非重言式的可满足式时，经过等值演算可将 A 化简，然后用观察法找到一个成真赋值，再找到一个成假赋值，就可判断 A 为非重言式的可满足式了。例如，对（6）用等值演算判断它的类型。 ( p ↔¬∧ p ) q q↔⇔ 0 （矛盾律） →∧→⇔ ( q q p ) ( )0 （等价等值式） ∨¬⇔ 0( q ) ∨¬∧ q ( ∨⇔ 1( q ¬∧ ) q q¬∧⇔ 1 )0 （蕴含等值式）（同一律）（零律） 6

q¬⇔ （同一律）到最后一步已将公式化得很简单。由此可知，无论 p 取 0 或 1 值，只要 q 取 0 值，原公式取值为 1，即 00 或 10 都为原公式的成真赋值，而 01，11 为成假赋值，于是公式为非重言式的可满足式。用主析取范式判断公式的类型也是万能的。A 为重言式当且仅当 A 的主析取范式含 n2 （ n 为 A 中所含命题变项的个数）个极小项；A 为矛盾式当且仅当 A 的主析取范式中不含任何极小项，记它的主析取范式为 0；A 为非重言式的可满足式当且仅当 A 的主析取范式中含极小项，但不是完全的。当命题变项较多时，用主析取范式法判公式的类型，运算量是很大的。用主合取范式判断公式的类型也是万能的。A 为重言式当且仅当 A 的主合取范式中不含任何极大项，此时记 A 的主合取范式为 1；A 为矛盾式当且仅当 A 的主合取范式含 n2 个极大项（ n 为 A 中含的命题变项的个数）；A 为非重言式的可满足式当且仅当 A 的主析取范式中含含极大项，但不是全部的。 1.8 （1）从左边开始演算 ( p ∧ q ) ∨ ( p ¬∧ q ) ∧⇔ p ( q ¬∨ q ) （分配律） 1∧⇔ p （排中律） .p⇔ （同一律）（2）从右边开始演算 p ∧→ q ( r ) ∨¬⇔ p ( q ∧ r ) （蕴含等值式） ∨¬⇔ p ( q ) ∨¬∧ p ( r ) （分配律） →∧→⇔ p q ) ( p ( r ). （蕴含等值式）（3）从左边开始演算 p ↔¬ ( q ) 7

→∧→⇔ (( q q p ( ) p )) ∨¬¬⇔ (( p ∧¬¬⇔ (( p q ) q ) ∨¬∨ p ( q )) ∨∧¬∨ p ) ( ( q ∨¬∧ q ) ( p ∧ q )) ∨¬∧¬¬⇔ (( q p ) ( p ∧ q )) ∨⇔ p ( q ) ∧¬∧ p ( q ). 请读者填上每步所用的基本等值式。本题也可以从右边开始演算 ( p ∨ q ) ∧¬∧ p ( q ) (( ¬¬⇔ p ∨ q ) ∧¬∧ p ( q ) ∨¬¬⇔ p ( ( q ) ( ¬¬∨ p ∧ q )) ∨¬∨¬¬⇔ (( q p ) ( p ∧ q )) ∧¬¬⇔ (( p q ) ∨¬∧ p ( q ) ∨¬∧ q ( p ) ∨¬∧ q ( q )) ∨∧¬⇔ 1( p q ) ∨¬∧ q ( p 1) ∧ →∧→¬⇔ (( q q p ( ) p )) p ↔¬⇔ ( q ). 读者填上每步所用的基本的等值式。 1.9 （1） (( ¬ p →∧ q ) p ) ∧¬¬⇔ p ( ( ∧¬¬⇔ p ( ( q ) ∨ p （蕴含等值式） q ) ∨ p ) （德·摩根律） ¬∧∧⇔ q p p （结合律、交换律） ∧¬∧⇔ p p ( ) q （矛盾式） .0⇔ （零律） 8

资料库

离散数学第三版课后答案.pdf

相关推荐

课程资源

热门标签

最新资料