具有轨道角动量的引力波.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书资料大小：0.41M 资料格式：pdf 举报版权申诉

weixin_38677806-12372955-4744300845195394619.pdf-第1页.png

第1页 / 共7页

weixin_38677806-12372955-4744300845195394619.pdf-第2页.png

第2页 / 共7页

weixin_38677806-12372955-4744300845195394619.pdf-第3页.png

第3页 / 共7页

weixin_38677806-12372955-4744300845195394619.pdf-第4页.png

第4页 / 共7页

weixin_38677806-12372955-4744300845195394619.pdf-第5页.png

第5页 / 共7页

weixin_38677806-12372955-4744300845195394619.pdf-第6页.png

第6页 / 共7页

weixin_38677806-12372955-4744300845195394619.pdf-第7页.png

第7页 / 共7页

Gravitational waves with orbital angular momentum

Abstract

1 Introduction

2 Gravitational wave beams

2.1 Laguerre–Gaussian (LG) beams

3 Effect of a passing gravitational wave beam on spacetime: possible detection

3.1 Effect of gravitational wave beams on laser-interferometer detectors

3.2 Detection scheme

4 Conclusions

Acknowledgements

References

Eur. Phys. J. C (2020) 80:326 https://doi.org/10.1140/epjc/s10052-020-7881-2 Letter Gravitational waves with orbital angular momentum Pratyusava Baral1,a, Anarya Ray2,b, Ratna Koley1,c 1 Department of Physics, Presidency University, Kolkata 700073, India 2 Department of Physics, University of Winsconsin, Milwaukee 53211, USA 3 School of Physical Sciences, Indian Association for the Cultivation of Science, Kolkata 700032, India , Parthasarathi Majumdar3,d Received: 4 October 2019 / Accepted: 27 March 2020 © The Author(s) 2020 Abstract Compact orbiting binaries like the black hole binary system observed in GW150914 carry large amount of orbital angular momentum. The post-ringdown compact object formed after merger of such a binary conﬁguration has only spin angular momentum, and this results in a large orbital angular momentum excess. One signiﬁcant possibility is that the gravitational waves generated by the system carry away this excess orbital angular momentum. An estimate of this excess is made. Arguing that plane gravitational waves cannot possibly carry any orbital angular momentum, a case is made in this paper for gravitational wave beams carrying orbital angular momentum, akin to optical beams. Restrict- ing to certain speciﬁc beam-conﬁgurations, we predict that such beams may produce a new type of strain, in addition to the longitudinal strains measured at aLIGO for GW150914 and GW170817. Current constraints on post-ringdown spins, derived within the plane-wave approximation of gravitational waves, therefore stand to improve. The minimal modiﬁcation that might be needed on a laser-interferometer detector (like aLIGO or VIRGO) to detect such additional strains is also brieﬂy discussed. 1 Introduction Gravitational waves (GWs) detected by the Advanced Laser Interferometer Gravitational Wave Observatory (aLIGO) [1– 3] have established the existence of inspiralling compact object binaries. Within General Relativity (GR), such sys- tems radiate gravitational waves, carrying energy and angular momenta [4,5], while spiraling into each other. The amount of angular momentum carried, as viewed by an observer at inﬁnity (assuming the space-time to be asymptotically ﬂat) a e-mail: baralpratyusava@gmail.com b e-mail: ronanarya9988@gmail.com c e-mail: ratna.physics@presiuniv.ac.in (corresponding author) d e-mail: bhpartha@gmail.com can be estimated by the difference in angular momentum of the initial and ﬁnal stages of a merger. GW150914 conﬁrmed the merger of two black holes separated by a radius of 210 km and of masses around 36 M and 29 M, forming a resul- tant Kerr black hole of mass ∼ 62 M and a spin parameter of ∼ 0.67 [1]. We estimate the rate of loss of orbital angular momentum by the coalescing binary, assuming the objects to be slowly moving, such that the quadrupole approximation to gravitational wave generation still holds. In this approxi- mation, the rate of loss of orbital angular momentum can be given as dr 2˙habx j ∂khab Qka ... d Li dt = c3 32π G = 2G 15c5 2G 15c5 i jk i jk ¨Q ja (μr 2)2ω5 (1) Inserting typical values for the masses (∼ 30 M) and the size of the compact binary (∼ 200 km), with the rotational angular frequency of about 10 Hz, the rate of loss of orbital angular momentum from the system is about 1034 Joules— which is quite large. An actual estimate of orbital angular momentum radiated closer to merger would include higher order modes and thus increase the number. From such an esti- mate, the motivations for a serious analysis towards the possi- bility of detection of such a large orbital angular momentum, carried by the gravitational waves, in current and forthcom- ing laser interferometer experiments are very strong. Measuring spacetime ﬂuctuations as a function of time only, aLIGO has successfully constrained source parame- ters from which one can calculate radiated angular momen- tum [9–11]. However a subtle issue arises if we want direct measurement of angular momentum at some future detec- tor. As we show in the sequel, monochromatic plane waves with spatially constant polarizations, used predominantly in detection analysis, cannot carry orbital angular momentum. 0123456789().: V,-vol 123

326 Page 2 of 7 Eur. Phys. J. C (2020) 80:326 Speciﬁcally, gravitational waves cannot reach the detector as monochromatic plane waves due to angular momentum con- servation. We stress that by the term ‘plane wave’ we mean, a monochromatic wave solution of the linearized, source-free Einstein equation, not only whose constant phase surfaces are planes in spacetime, but also whose polarizations are spa- tially constant, as the wave propagates. Taking a clue from well established results in optics [12–16], we propose gravi- tational radiation with some phase structure or gravitational wave beams as a basis for expansion of the source wave- form for detection analysis. The phase structure would enable us to measure orbital angular momentum directly. Recently, radiation from a spiralling charged particle [17,18] carrying orbital angular momentum in the context of classical electro- dynamics, has been shown to possess a similar phase struc- ture. There exist other motivational aspects of directly measur- ing angular momentum from gravitational waves. A direct measurement of orbital angular momentum would provide us with an estimate of its rate of loss from the inspiralling binary. This, in turn, might allow us to impose additional constraints on the parameters over and above those obtained by cross-correlation with various templates. This would fur- ther enable us to settle many controversies relating to various mergers [20] like GW170817 [3] (NS–NS merger) which are expected to be routine in the near future. Using this, we may also expect to put constraints on the exotic alternative com- pact objects like fuzz balls [21], gravastars [22,23], worm- holes [24], boson stars [25] and so on, and hence be able to ascertain better the actual composition of the coalescing binary. Comparing how well the estimated angular momen- tum loss of the system compares to the angular momen- tum carried by gravitational waves as detected by a faraway observer, additional restrictions on the validity of GR in the linearized regime may perhaps be ascertained. Lastly, the third-generation run of the aLIGO and VIRGO is expected to detect certain gravitational lensing events [19]. An additional probe of angular momentum is expected to give us additional knowledge of the medium through which it passes. This may vastly improve our understanding of interactions of gravita- tional waves with matter as it passes through astrophysical objects such as stars or galactic clusters. However for the time-being, we focus on a direct independent study of orbital angular momentum carried by gravitational waves. In this paper we examine the analytic structure of grav- itational waves in the linearized regime, starting from the gauge ﬁxed linearized vacuum Einstein equation. We further demand solutions that carry orbital angular momentum (We prove that plane waves do not carry orbital angular momen- tum in the next section). This naturally enables us to go beyond plane waves and discuss gravitational wave beams. However our solutions are well within the regime of Gen- eral Relativity and does not take any modiﬁed gravity effect 123 into account. We show en passant that plane waves cannot carry orbital angular momentum, implying that recourse to gravitational wave beams is imperative. We choose a par- ticular set of linearly independent beams which form a basis for gravitational waves with orbital angular momentum. Any gravitational radiation generated by sources within general relativity can be expanded in this beam basis. A brief dis- cussion is presented on the effects these beams would have on spacetime. We also give a schematic outline, how these beams carrying orbital angular momentum may be detected and the contribution of the beam to the overall signal mea- sured in a generic Laser-interferometer gravitational wave detector. 2 Gravitational wave beams We employ here the linearized tetrad formalism [27] for dis- cussing gravitational waves, for two reasons: the ease to dis- cuss fermionic interactions in astrophysically relevant quan- tum ﬁeld theoretic analysis, and to understand better the tran- sition from local Lorentz invariance to global Lorentz sym- metry under linearization—a phenomenon which remains slightly obscure within the metric formalism. However, the prescription to change to metric computations is included, for the ease of the readers. For the purpose of linearization, the spacetime tetrad com- a are decomposed as eμa = eμa + εμa, where ponents eμ eμa is the background Minkowski spacetime tetrad and as, ea εμa is the linear ﬂuctuation. Linearized gravity in the har- monic gauge using this perturbed tetrad can be expressed ν2εaμ = 0 where Greek indices specify spacetime labels and early Latin indices are tangent space labels. The late Latin indices are reserved for three dimen- sional space. Therefore, the metric and ﬂuctuations turns out to be μ2εaν +ea ημν = ηabea μeb μεaν +ea hμν =ea ν ν εaμ + O(ε2) (2) (3) Equation (3) explicitly states how to transform from the met- ric ﬂuctuations to the tetrad ﬂuctuations and vice-versa. The gauge ﬁxed linearized tetrad equation admits a wave like solution given by, εaμ = ϑaμ(x σ ) exp(ikλx λ) + ϑ∗ aμ(x σ ) exp(−ikλx λ) (4) ∗ ) representing complex conjugation. This with the asterisk ( solution imposed on linearized tetrad equation gives, (∂ ν ∂ν + 2ikν ∂ ν ) ϑaμ(x) = 0. (5)

Eur. Phys. J. C (2020) 80:326 Page 3 of 7 326 The Lagrangian density and the energy-momentum tensor for linearized gravity [28] are L = − c4 32π G T μν = c4 16π G (∂ μεaσ ∂μεaσ +ea (∂ μεaσ ∂ ν εaσ +ea σebρ ∂ μεaρ ∂μεb σebρ ∂ μεaρ ∂ ν εb σ ) σ ) (6) (7) Since we are dealing with small ﬂuctuations around a Minkowski spacetime tetrad in the linearized region, the sys- tem is globally Lorentz-symmetric. The conserved Noether charge density corresponding to this symmetry can be expressed as, Mρσ = ˙εaμ[x[ρ|(∂|σ]εaμ +ea νebμ∂|σ]εb ν )] (8) 8π G c2 where, over dot represents time derivative, and the square brackets denote anti-symmetry. Integrating this charge den- sity over all space gives the inﬁnitesimal Lorentz generators. If ϑaμ is not a function of the spatial coordinates (xi ) (xi k j − on integration the ﬁrst term reduces to terms like x j ki )d3x; with the integration measure being clearly rota- tionally invariant, the ﬁrst term vanishes by spatial rotational invariance ! This implies that a spatially constant polariza- tion, like for plane waves in our connotation [which deﬁnitely satisfy Eq. (5)], cannot carry orbital angular momentum. It follows that for gravitational waves to carry orbital angular momentum, their polarization tensors must themselves be tensor ﬁelds. One way to enable polarization ﬁelds in grav- itational waves is through gravitational wave beams, akin to optical beams. Plane waves deﬁnitely carry spin angu- lar momentum. But the spin angular momentum density is miniscule, and deﬁnitely cannot account for all angular momentum radiated. Moreover the spin part is a property of the radiation and can never be zero for a rank two tensor ﬁeld. The orbital angular momentum is dependent on orien- tation of objects and ﬁelds and thus somewhat arbitrary. Thus there is no reason to expect that orbital angular momentum of source is getting converted to spin angular momentum of the wave. Thus we are looking for the most general solution of linearized vacuum Einstein ﬁeld equations. 2.1 Laguerre–Gaussian (LG) beams Let z direction be the direction of propagation of the grav- itational wave beam. Since any conceivable detector has to be placed far away from the sources, we can safely assume the beam to be paraxial (kz ≈ k) [14,15]. So Eq. 5 can be expressed as (∇T where ∇T 2 is a two dimensional Laplace operator in the plane perpendicular to z. The paraxial approximation also guarantees that the change in polarization tensor in the 2 + ∂ z∂z − ∂t ∂t + 2ikz∂ z − 2ikt ∂t ) ϑaμ(x) = 0 (9) r 2 T = 1 r ∂2ϑ aμ kz direction of propagation is negligible in comparison to the . So Eq. (9) reduces to, wave vector (∇T 2+ 2ikz∂ z) ϑaμ(x) = 0. We choose the transverse plane ∂r + ∂r to be spanned by (r, φ) then ∇2 2 + 1 ∂ϑ aμ ∂z2 ∂φ 2. ∂z For simplicity, we choose to work with one particular com- ponent of ϑaμ and for the time being we drop the spacetime and tangent space indices. A solution of the form √ −ikr 2z 2r 2(z2 + z2 w(z) imφ − i (2 p + |m| + 1) tan −r 2 ϑmp(r, φ, z) = Amp w(z) × exp × exp |m| p 2r 2 w2(z) −1 z z R |m| exp (10) L R ) w2(z) λ 2π z z R 2 λ . L where and k ≈ kz = 2π satisﬁes Eq. (9) in its paraxial form [15] with m, p taking integer values referring to various modes. The radius of the 1 + beam w(z) is given by w(z) = w(0) |m| z R = π w(0) p (x) is the associated Laguerre polynomial while Amp is a normalization constant. By deﬁnition of Laguerre polynomials, p has to be an integer. The single valuedness of the ﬁeld under a rotation of π radian forces the azimuthally dependent phase factor to be quantized with m taking only integral values. The Laguerre–Gaussian modes are orthonormal in both labels m & p such that rdr ϑmp(r, φ, z)[ϑqr (r, φ, z)]∗ = δmq δ pr . ∞ 0 This guarantees that the LG modes form a complete orthonor- mal family which can be used as a basis for a beam with an arbitrary polarization distribution. These beams exhibit a symmetry manifest in the use of cylindrical coordinates. Any other choice of a complete set of beams a different sym- metry (like, e.g., the Bessel beam) is equally valid; these beams can of course be expressed as a linear combination of LG modes. Since our solutions form a basis, any waveform including plane waves or spherical waves can be expanded in our basis. dφ 0 The orbital angular momentum density can be expressed in a simple form which follows directly from Eq. (8), L = d3x − l ω |ϑmp|2ˆr + r c z r + l ω |ϑmp|2ˆz − 1 |ϑmp|2 ˆφ z2 z2+z2 R (11) Such solutions also exist in the case of electromagnetic waves and have been extensively studied in Refs. [12– 16]. Bialynicki-Birula et al. [29] have also discussed GW beams using an electromagnetic-gravitational correspon- dence within a spinoral formalism. In this work we take an 123

326 Page 4 of 7 Eur. Phys. J. C (2020) 80:326 approach that appears to be more convenient for phenomeno- logical applications. Integrating the angular momentum density (11) over all space, we get the total angular momentum. As stated earlier our analysis is only valid in the weak ﬁeld regime. So, the integration domain must be restricted to that regime. Here we should mention the caveat that unlike in laser optics, w(0) has no signiﬁcance and is just a free parameter of the chosen basis. 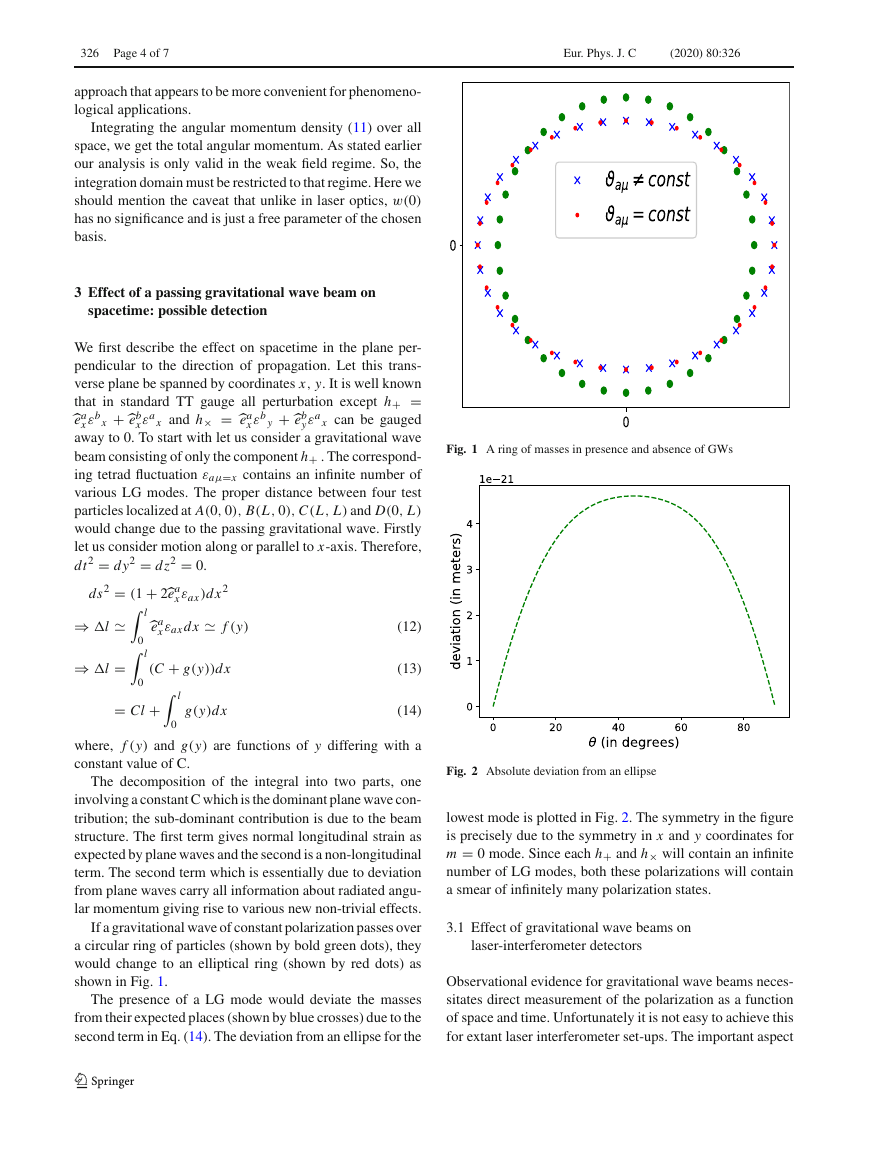3 Effect of a passing gravitational wave beam on spacetime: possible detection Fig. 1 A ring of masses in presence and absence of GWs εa εa εb x x + eb x y + eb y x and h× = ea We ﬁrst describe the effect on spacetime in the plane per- pendicular to the direction of propagation. Let this trans- verse plane be spanned by coordinates x, y. It is well known that in standard TT gauge all perturbation except h+ = ea εb x can be gauged x away to 0. To start with let us consider a gravitational wave beam consisting of only the component h+ . The correspond- ing tetrad ﬂuctuation εaμ=x contains an inﬁnite number of various LG modes. The proper distance between four test particles localized at A(0, 0), B(L , 0), C(L , L) and D(0, L) would change due to the passing gravitational wave. Firstly let us consider motion along or parallel to x-axis. Therefore, dt 2 = dy2 = dz2 = 0. ds2 = (1 + 2ea ea ⇒ l ⇒ l = (C + g(y))dx εax dx f (y) εax )dx 2 l l 0 0 (12) (13) x x l = Cl + g(y)dx 0 (14) f (y) and g(y) are functions of y differing with a where, constant value of C. The decomposition of the integral into two parts, one involving a constant C which is the dominant plane wave con- tribution; the sub-dominant contribution is due to the beam structure. The ﬁrst term gives normal longitudinal strain as expected by plane waves and the second is a non-longitudinal term. The second term which is essentially due to deviation from plane waves carry all information about radiated angu- lar momentum giving rise to various new non-trivial effects. If a gravitational wave of constant polarization passes over a circular ring of particles (shown by bold green dots), they would change to an elliptical ring (shown by red dots) as shown in Fig. 1. The presence of a LG mode would deviate the masses from their expected places (shown by blue crosses) due to the second term in Eq. (14). 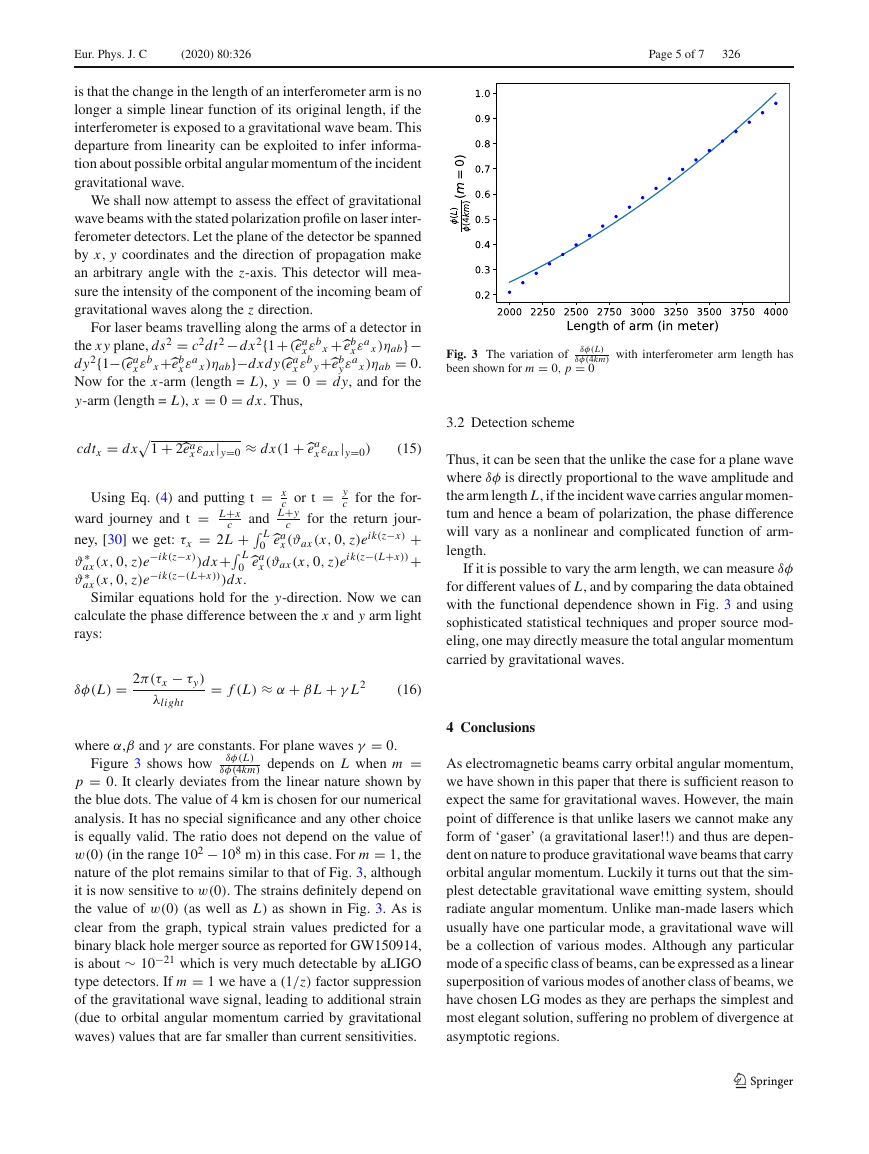The deviation from an ellipse for the 123 Fig. 2 Absolute deviation from an ellipse lowest mode is plotted in Fig. 2. The symmetry in the ﬁgure is precisely due to the symmetry in x and y coordinates for m = 0 mode. Since each h+ and h× will contain an inﬁnite number of LG modes, both these polarizations will contain a smear of inﬁnitely many polarization states. 3.1 Effect of gravitational wave beams on laser-interferometer detectors Observational evidence for gravitational wave beams neces- sitates direct measurement of the polarization as a function of space and time. Unfortunately it is not easy to achieve this for extant laser interferometer set-ups. The important aspect

Eur. Phys. J. C (2020) 80:326 Page 5 of 7 326 is that the change in the length of an interferometer arm is no longer a simple linear function of its original length, if the interferometer is exposed to a gravitational wave beam. This departure from linearity can be exploited to infer informa- tion about possible orbital angular momentum of the incident gravitational wave. We shall now attempt to assess the effect of gravitational wave beams with the stated polarization proﬁle on laser inter- ferometer detectors. Let the plane of the detector be spanned by x, y coordinates and the direction of propagation make an arbitrary angle with the z-axis. This detector will mea- sure the intensity of the component of the incoming beam of gravitational waves along the z direction. εb εb x εa x x+eb x +eb y+eb the x y plane, ds2 = c2dt 2− dx 2{1+ (ea For laser beams travelling along the arms of a detector in x )ηab}− dy2{1−(ea x )ηab}−dxdy(ea x )ηab = 0. x εb Now for the x-arm (length = L), y = 0 = dy, and for the y-arm (length = L), x = 0 = dx. Thus, εax|y=0 ≈ dx(1 +ea cdtx = dx 1 + 2ea εax|y=0) (15) εa x εa y x x x c Using Eq. (4) and putting t = x c or t = y c for the for- and L+y ward journey and t = L+x ney, [30] we get: τx = 2L + for the return jour- ea (ϑax (x, 0, z)eik(z−x) + −ik(z−x))dx+ ea (ϑax (x, 0, z)eik(z−(L+x))+ ϑ∗ −ik(z−(L+x)))dx. ϑ∗ (x, 0, z)e ax (x, 0, z)e ax Similar equations hold for the y-direction. Now we can calculate the phase difference between the x and y arm light rays: L 0 L 0 c x x δφ (L) = 2π(τx − τy) λlight = f (L) ≈ α + β L + γ L2 (16) where α,β and γ are constants. For plane waves γ = 0. δφ (4km) depends on L when m = Figure 3 shows how δφ (L) p = 0. It clearly deviates from the linear nature shown by the blue dots. The value of 4 km is chosen for our numerical analysis. It has no special signiﬁcance and any other choice is equally valid. The ratio does not depend on the value of w(0) (in the range 102 − 108 m) in this case. For m = 1, the nature of the plot remains similar to that of Fig. 3, although it is now sensitive to w(0). The strains deﬁnitely depend on the value of w(0) (as well as L) as shown in Fig. 3. As is clear from the graph, typical strain values predicted for a binary black hole merger source as reported for GW150914, is about ∼ 10 −21 which is very much detectable by aLIGO type detectors. If m = 1 we have a (1/z) factor suppression of the gravitational wave signal, leading to additional strain (due to orbital angular momentum carried by gravitational waves) values that are far smaller than current sensitivities. Fig. 3 The variation of been shown for m = 0, p = 0 δφ (L) δφ (4km) with interferometer arm length has 3.2 Detection scheme Thus, it can be seen that the unlike the case for a plane wave where δφ is directly proportional to the wave amplitude and the arm length L, if the incident wave carries angular momen- tum and hence a beam of polarization, the phase difference will vary as a nonlinear and complicated function of arm- length. If it is possible to vary the arm length, we can measure δφ for different values of L, and by comparing the data obtained with the functional dependence shown in Fig. 3 and using sophisticated statistical techniques and proper source mod- eling, one may directly measure the total angular momentum carried by gravitational waves. 4 Conclusions As electromagnetic beams carry orbital angular momentum, we have shown in this paper that there is sufﬁcient reason to expect the same for gravitational waves. However, the main point of difference is that unlike lasers we cannot make any form of ‘gaser’ (a gravitational laser!!) and thus are depen- dent on nature to produce gravitational wave beams that carry orbital angular momentum. Luckily it turns out that the sim- plest detectable gravitational wave emitting system, should radiate angular momentum. Unlike man-made lasers which usually have one particular mode, a gravitational wave will be a collection of various modes. Although any particular mode of a speciﬁc class of beams, can be expressed as a linear superposition of various modes of another class of beams, we have chosen LG modes as they are perhaps the simplest and most elegant solution, suffering no problem of divergence at asymptotic regions. 123

326 Page 6 of 7 Eur. Phys. J. C (2020) 80:326 In this paper, in addition to showing the necessity of con- sidering gravitational wave beams in place of plane waves in order to explain the orbital angular momentum emitted via gravitational waves, by the merger of inspiralling com- pact binaries, we have presented an account of the effects these gravitational wave beams will have on spacetime in general and on laser interferometer detectors. Further, per- haps for the ﬁrst time, we have proposed a schematic way of measuring the phase structure of gravitational radiation, by incorporating minimal changes in extant interferometers. Since the orbital angular momentum of gravitational waves can be directly calculated from these amplitudes, we have thus, again for the ﬁrst time, proposed a schematic method of direct measurement of angular momentum carried by grav- itational waves. We are primarily interested in the lowest order mode, because the ﬁrst higher mode for GW150914 like sources will have non-unique values of strains dependent on the normalization factor w(0) and primarily because we have a 1/zm-suppression. This might make the interference signal too weak to detect. Having said that though, the expressions are dependent on various non-linear parameters and a par- ticular set of w(0); tweaking the frequency and distance it may be possible to produce such additional strains for higher modes, which are more realistic. The idea of gravitational wave beams is at its infancy and thus lot of work remains to be done. From the values of the plus and cross polarizations at asymptotic regions obtained from various numerical simulations one might try to estimate various beam parameters. Since the beams form a complete basis, any wave form predicted by numerical relativity can always be expanded in terms of the beams by computing the overlap integrals and the corresponding beam parameters measured via the scheme discussed in this paper. This would enable us to understand if data from a ﬁxed length detector is sufﬁcient to determine the beam parameters uniquely with a little degeneracy. Although this work is yet to be done, our intuition suggests that the deviation from plane waves will not become apparent due to their smallness until we have some way to vary the length of detectors. However a more rigorous calculation is left to be done before making any concrete statement. Moreover the solution presented here involves the paraxial approximation. It is possible to get exact solutions of the vacuum linearized Einstein’s equations beyond the paraxial approximation, which still carry orbital angular momentum and form a complete basis. This is currently under study. Acknowledgements The authors would like to thank Soumendra Kishore Roy and Sk. Sajid of Presidency University, Kolkata for valu- able discussions and inputs. R. Koley acknowledges WBDHESTBT research fund. PB and AR would like to thank Bala Iyer of ICTS, K. G. Arun and J. Haque of CMI,India and A. Gupta of Pennsylvania State University for discussions in the IAGRG meeting 2018. PB is grateful 123 to Luc Blanchet for a discussion at the 2019 ICTS Summer School on Gravitational Waves regarding total orbital angular momentum radiated away through gravitational waves. Data Availability Statement This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Since we have a complete basis any waveform (including plane waveform) can be described using our solution. So in principle using the present LIGO- Virgo detectors we can estimate our beam parameters. But the issue that needs to be checked is if the parameter space is degenerate or not. Moreover increasing number of parameters will naturally improve the likelihood function, and thus one requires detailed statistical analysis of the parameters before blindly estimating it. We plan to work on this in the near future and hope to come up with a more concrete statement on the detectability of beam parameters from ﬁxed length detectors.] Open Access This article is licensed under a Creative Commons Attri- bution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, pro- vide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indi- cated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permit- ted use, you will need to obtain permission directly from the copy- right holder. To view a copy of this licence, visit http://creativecomm ons.org/licenses/by/4.0/. Funded by SCOAP3. References 1. B.P. Abbott et al., Phys. Rev. Lett. 116, 241102 (2016). arXiv:1610.02182 [gr-qc] 2. B.P. Abbott et al., Phys. Rev. Lett. 118, 221101 (2017). arXiv:1706.01812 [gr-qc] 3. B.P. Abbott et al., Phys. Rev. Lett. 119, 161101 (2017). arXiv:1710.05832 [gr-qc] 4. A. Einstein, Sitzungsber. K. Preuss. Akad. Wiss. 1, 688 (1916) 5. A. Einstein, Sitzungsber. K. Preuss. Akad. Wiss 1, 154 (1918) 6. S. Stevenson et al., Nat Commun. (2017). https://doi.org/10.1038/ ncomms14906 arXiv:1704.01352 [astro-ph.HE] 7. I. Mandel, A. Farmer. arXiv:1806.05820 [astro-ph.HE] 8. I. Bialynicki-Birula, S. Charzy´nski, Phys. Rev. Lett. 121, 171101 (2018). arXiv:1810.02219 [gr-qc] 9. K. Thorne, Rev. Mod. Phys. 52, 299 (1980) 10. T.W. Baumgarte, S.L. Shapiro, Numerical Relativity: Solving Ein- stein’s Equations on the Computer, 1st edn. (Cambridge University Press, Cambridge, 2010) 11. M. Shibata, Numerical Relativity (100 Years of General Relativity) (World Scientiﬁc Publishing Company, New York, 2015) 12. L. Allen et al., Phys. Rev. A 45(11), 8185–8190 (1992). (reprinted in [57, Paper 2.1]) 13. A.M. Yao, M.J. Padgett, Adv. Opt. Phot. 3, 161 (2011) 14. J.B. Gotte, S.M. Barnett, in Light Beams Carrying Orbital Angular Momentum, ed. by Andrews, D., Babiker, M. The Angular Momen- tun of Light, 1st edn. (Cambridge University Press, Cambridge, 2013) 15. H.A. Haus, Waves and Fields in Optoelectronics (Chapter 5) (Prentice-Hall Inc., New York, 1984) 16. D.S. Simon, A Guided Tour of Light Beams (Morgan & Claypool Publishers (IOP concise physics), New York, 2016)

Eur. Phys. J. C (2020) 80:326 Page 7 of 7 326 17. M. Katoh et al., Phys. Rev. Lett. 118, 094801 (2017). arXiv:1610.02182 [physics.optics] 18. V. Epp, U. Guselnikova, Phys. Lett. A 383(22), 2668–2671 (2019) 19. Christian et al., Phys. Rev. D 10, 103022 (2018). arXiv:1802.02586 28. M. Maggiore, in Gravitational Waves: Theory and Experiments. Oxford Master Series in Physics, vol. 1 (Oxford University Press, Oxford, 2007) 29. I. Bialynicki-Birula, Z. Bialynicka-Birula, New J. Phys. 18, 023022 [astro-ph.HE] 20. H. Yang et al., arXiv:1710.05891 [gr-qc] 21. S.D. Mathur, Fortsch. Phys. 53, (2016). arXiv:1511.08909v1 [gr-qc] 30. B. Schutz, A First Course in General Relativity, 2nd edn. (Cam- 793–827 (2005). bridge University Press, Cambridge, 2009) arXiv:hep-th/0502050 [hep-th] 22. P. O. Mazur, E. Mottola, arXiv:gr-qc/109035 [gr-qc] 23. C. Chirenti, L. Rezzolla, Phys. Rev. D 94, 084016 (2016). arXiv:1602.08759 [gr-qc] 24. T. Damour, S.N. Solodukhin, Phys. Rev. D 76, 024016 (2007). arXiv:0704.2667 [gr-qc] 25. R. Rufﬁni, S. Bonazzola, Phys. Rev. 187, 1767–1783 (1969) 26. Z. Mark et al., Phys. Rev. D 96, 084002 (2017). arXiv:1706.06155 [gr-qc] 27. J. Yepez, arXiv:1106.2037 [gr-qc] 123

分享到：

赞收藏

资料库

具有轨道角动量的引力波.pdf

相关推荐

开发技术

热门标签

最新资料