第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
《计算机图形学》实验报告（C++）.doc
计算机科学系实验报告 （首页）
课程名称
计算机图形学
班 级 06 计算机科学与技术
实验名称 计算机图形学综合实验 指导教师
季军杰
学 号 061401102 日 期 2009 年 6 月 6 日
姓名 蔡晓源
____________________________________________________________
一、实验目的
理解并编写下面的四个算法：
① 直线 Bresenham 算法
② 圆 Bresenham 算法
③ 画饼分图
④ 区域着色
二、实验设备与环境
PC 机、Windows XP 操作系统、Visual C++6.0
三、实验内容、程序清单及运行结果
(详见附页)
四、实验结论、实验体会
实验结论：通过各种不同的算法，可以用强大的 C++语言在 MFC 框架上绘制各种各样的图形。
实验体会：通过自己亲身动手去做计算机图形学的这四个实验：直线 Bresenham 算法、圆 Bresenham
算法、画饼分图和区域着色，使我很好的加深了对本门课程的认识和理解；但是由于之前自己没接触
过有关图形学的相关知识和算法，所以刚开始感觉有点难以入手，不过后来通过查阅图书馆的相关资
料和请教任课老师，花了一定的时间去理解各种不同算法的思想，也参考了一些关键算法的源代码，
在看懂了之后修改了里面相应的源程序，使之完全符合本次实验的要求。
总之，这次图形学的实验确实使我受益匪浅！有付出才有收获，只有真正通过自身努力的东西才是
自己的！
计算机科学系实验报告
（附页）
三、算法说明、程序清单及运行结果
3.1 直线 Bresenham 算法
①算法说明
算法思想：
（1） 画点（xi,yi）,dx=x2-x1,dy=y2-y1,计算误差初值 P1=2dy-dx,i=1。
（2） 求直线的下一点位置 xi+1=xi+1，如果 Pi>0，则 yi+1=yi+1，否则 Pi+1=Pi+2dy。
（3） 画点（xi+1,yi+1）。
（4） 求下一个误差 Pi+1，如果 Pi>0，则 Pi+1=Pi+2dy-2dx，否则 Pi+1=Pi+2dy。
（5） i=i+1；如果 i=0)s1=1;else s1=1;
if(y2-y1>=0)s2=-1;else s2=-1;
if(deltay>deltax){
temp=deltax;
deltax=deltay;
deltay=temp;
interchange=1;
}
else interchange=0;
//f 为误差初值
f=2*deltay-deltax;
pDC->SetPixel(x,y,c);
for(i=1;i<=350;i++){
if(f>=0){
if(interchange==1)x+=s1;
else y+=s2;
pDC->SetPixel(x,y,c);
f=f-2*deltax;
}
else{
if(interchange==1)y+=s2;
else x+=s1;
f=f+2*deltay;
}
}
}
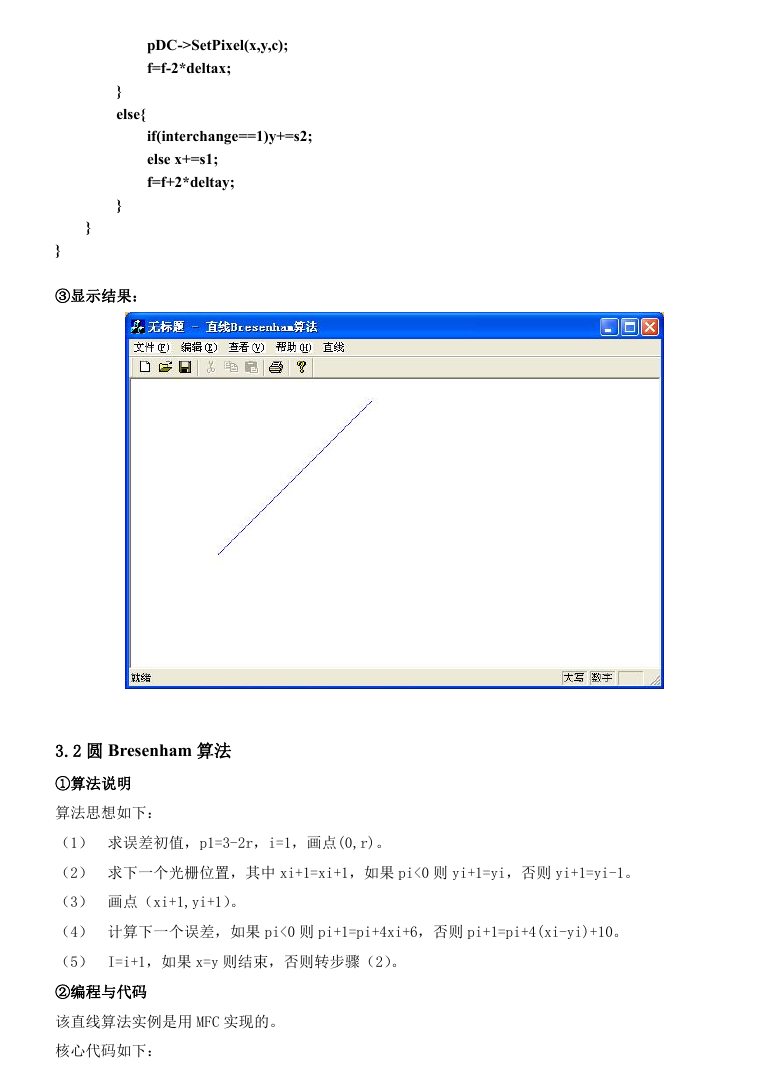
③显示结果：
3.2 圆 Bresenham 算法
①算法说明
算法思想如下：
（1） 求误差初值，p1=3-2r，i=1，画点(0,r)。
（2） 求下一个光栅位置，其中 xi+1=xi+1，如果 pi<0 则 yi+1=yi，否则 yi+1=yi-1。
（3） 画点（xi+1,yi+1）。
（4） 计算下一个误差，如果 pi<0 则 pi+1=pi+4xi+6，否则 pi+1=pi+4(xi-yi)+10。
（5） I=i+1，如果 x=y 则结束，否则转步骤（2）。
②编程与代码
该直线算法实例是用 MFC 实现的。
核心代码如下：
void CMainFrame::OnBresenhamcircle()
{
// TODO: Add your command handler code here
CDC* pDC=GetDC();
int xc=200,yc=200,radius=100,c=RGB(0,0,255);
int x1=0,y1=radius,p=3-2*radius;
while(x1SetPixel(xc+x1,yc+y1,c);
pDC->SetPixel(xc-x1,yc+y1,c);
pDC->SetPixel(xc+x1,yc-y1,c);
pDC->SetPixel(xc-x1,yc-y1,c);
pDC->SetPixel(xc+y1,yc+x1,c);
pDC->SetPixel(xc-y1,yc+x1,c);
pDC->SetPixel(xc+y1,yc-x1,c);
pDC->SetPixel(xc-y1,yc-x1,c);
if(p<0)
p=p+4*x1+6;
else
{
p=p+4*(x1-y1)+10;
y1-=1;
}
x1+=1;
}
if(x1==y1)
pDC->SetPixel(xc+x1,yc+y1,c);
pDC->SetPixel(xc-x1,yc+y1,c);
pDC->SetPixel(xc+x1,yc-y1,c);
pDC->SetPixel(xc-x1,yc-y1,c);
pDC->SetPixel(xc+y1,yc+x1,c);
pDC->SetPixel(xc-y1,yc+x1,c);
pDC->SetPixel(xc+y1,yc-x1,c);
pDC->SetPixel(xc-y1,yc-x1,c);
}
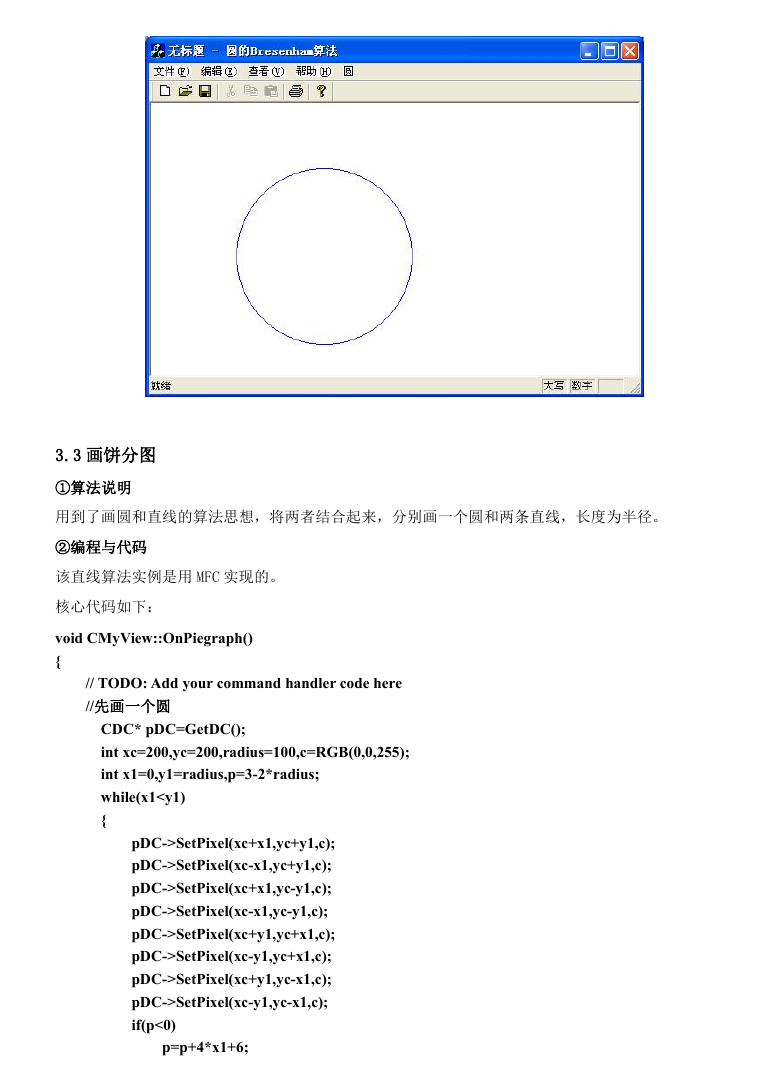
③显示结果：
3.3 画饼分图
①算法说明
用到了画圆和直线的算法思想，将两者结合起来，分别画一个圆和两条直线，长度为半径。
②编程与代码
该直线算法实例是用 MFC 实现的。
核心代码如下：
void CMyView::OnPiegraph()
{
// TODO: Add your command handler code here
//先画一个圆
CDC* pDC=GetDC();
int xc=200,yc=200,radius=100,c=RGB(0,0,255);
int x1=0,y1=radius,p=3-2*radius;
while(x1SetPixel(xc+x1,yc+y1,c);
pDC->SetPixel(xc-x1,yc+y1,c);
pDC->SetPixel(xc+x1,yc-y1,c);
pDC->SetPixel(xc-x1,yc-y1,c);
pDC->SetPixel(xc+y1,yc+x1,c);
pDC->SetPixel(xc-y1,yc+x1,c);
pDC->SetPixel(xc+y1,yc-x1,c);
pDC->SetPixel(xc-y1,yc-x1,c);
if(p<0)
p=p+4*x1+6;
else
{
p=p+4*(x1-y1)+10;
y1-=1;
}
x1+=1;
}
if(x1==y1)
pDC->SetPixel(xc+x1,yc+y1,c);
pDC->SetPixel(xc-x1,yc+y1,c);
pDC->SetPixel(xc+x1,yc-y1,c);
pDC->SetPixel(xc-x1,yc-y1,c);
pDC->SetPixel(xc+y1,yc+x1,c);
pDC->SetPixel(xc-y1,yc+x1,c);
pDC->SetPixel(xc+y1,yc-x1,c);
pDC->SetPixel(xc-y1,yc-x1,c);
//画一条直线，作为圆的半径
int x3=100,y3=200,x4=200,y4=300;
int i,s1,s2,interchange;
int x,y,deltax,deltay,f,temp;
x=200;
y=200;
deltax=abs(x4-x3);
deltay=abs(y4-y3);
if(x4-x3>=0)s1=1;else s1=1;
if(y4-y3>=0)s2=-1;else s2=-1;
if(deltay>deltax){
temp=deltax;
deltax=deltay;
deltay=temp;
interchange=1;
}
else interchange=0;
f=2*deltay-deltax;
pDC->SetPixel(x,y,c);
for(i=1;i<=142;i++){
if(f>=0){
if(interchange==1)x+=s1;
else y+=s2;
pDC->SetPixel(x,y,c);
f=f-2*deltax;
if(interchange==1)y+=s2;
}
else{
else x+=s1;
f=f+2*deltay;
}
}
//再画一条半径
int x5=100,y5=300,x6=200,y6=400;
int j,s3,s4,interchange1;
x=200;
y=200;
deltax=abs(x6-x5);
deltay=abs(y6-y5);
if(x6-x5>=0)s3=1;else s3=-1;
if(y6-y5>=0)s4=1;else s4=-1;
if(deltay>deltax){
temp=deltax;
deltax=deltay;
deltay=temp;
interchange=1;
}
else interchange=0;
f=2*deltay-deltax;
pDC->SetPixel(x,y,c);
for(i=1;i<=142;i++){
if(f>=0){
if(interchange==1)x+=s3;
else y+=s4;
pDC->SetPixel(x,y,c);
f=f-2*deltax;
if(interchange==1)y+=s4;
else x+=s3;
f=f+2*deltay;
}
else{
}
}
}
③显示结果：
3.4 区域着色
①算法说明
扫描线种子填充算法思想：
（1） 栈顶像素出栈。
（2） 沿扫描线对出栈像素的左右像素进行填充，直至遇到边界像素为止，即每出栈一个像素，就对
包含该像素的整个区间进行填充。
（3） 上述区间内最左、最右的像素分别记为 xl、xr。
（4） 在区间[xl,xr]中检查与当前扫描线相邻的上下两条扫面线的有关像素是否全为边界像素或已
填充的像素，若存在非边界、未填充的像素，则把每一区间的最右像素取作种子像素入栈。
②编程与代码
该区域着色实例是用 MFC 实现的，先绘画一个正方形，然后用种子填充法进行内部颜色填充。
核心代码如下：（需先在头文件 AreaView.h 中的 Public 下添加 CPoint
spt[4];）
void CMyView::OnLButtonDblClk(UINT nFlags, CPoint point)
{
// TODO: Add your message handler code here and/or call default
RedrawWindow();
CDC* pDC=GetDC();
CPen newpen(PS_SOLID,1,RGB(255,0,0));
CPen *old=pDC->SelectObject(&newpen);
//正方形各顶点的坐标
spt[0]=CPoint(150,150);
spt[1]=CPoint(150,300);
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
