论文研究-蚁群算法在定向问题中的应用 .pdf

发布时间：2022-05-30 发布人：admin 分类：说明书资料大小：0.27M 资料格式：pdf 举报版权申诉

weixin_39841365-11559402-16359647707119001323.pdf-第1页.png

第1页 / 共6页

weixin_39841365-11559402-16359647707119001323.pdf-第2页.png

第2页 / 共6页

weixin_39841365-11559402-16359647707119001323.pdf-第3页.png

第3页 / 共6页

weixin_39841365-11559402-16359647707119001323.pdf-第4页.png

第4页 / 共6页

weixin_39841365-11559402-16359647707119001323.pdf-第5页.png

第5页 / 共6页

weixin_39841365-11559402-16359647707119001323.pdf-第6页.png

第6页 / 共6页

文本预览

http://www.paper.edu.cn 蚁群算法在定向问题中的应用1 柯良军,冯祖仁西安交通大学机械制造系统工程国家重点实验室，西安 (710049) E-mail：fzr9910@xjtu.edu.cn 摘要：在极大极小蚁群系统的基础上，提出了一个求解定向问题的蚁群算法.给出了一种刻画两个解之间差异的距离.利用这种距离，提出了自适应更新信息素下界和自适应重新初试化信息素两种方法来避免停滞，其基本思想是使得构造的解与优解的距离足够大。实验结果表明：与 Chao 等人提出的算法相比较，蚁群算法能快速地求得高质量的解；并且所提出的方法能有效避免停滞，从而改进蚁群搜索能力。关键词：蚁群算法；定向问题；距离中图分类号：TP18 1．引言 , ) } = V E j V ∈ i {( , ) , i j 给定图 ( = G V E n , } ,边集 = 。任意两点i 和 j 的距离为 ijc 0 ,点集 {1, = L s 起点为点 1，终点为点 n , 并且 1 。每经过一个点可获得相应点的分数且每个点最多可经过一次。定向问题的优化目标是寻找一条从点 1 出发到点 n 终止的路径，使得所获得的总分数最高且路径长度不超过 maxT 。对于 ijx n ≤ ）, j 如果经过了边( , ) 等于 1, 否则为 0。则定向问题的数学描述为：。每个点 i 具有分数 is 。 ,则 ijx （1 s= n ,i ≤ j i max n n ∑∑ s x i ij i 1 = j 1 = s.t. x ik = n 1 − ∑ i = 2 n ∑ j = 2 x 1 j = n 1 − ∑ i 1 = x in = 1, n 1 − ∑ j = 2 x kj ≤ 1, k = 2, L , n − 1, (1) (2) (3) (4) ≤ T max , n n c x ij ij ∑∑ i 1 = i {0,1}, , ∈ 1 = j ijx j 1, = L , n . (5) 定向问题来自于定向运动。许多实际问题可以归结为定向问题[1, 2]。迄今为止，人们提出了许多求解该问题的精确算法。文献[3]中用整数规划来求解，文献[4]采用了割平面技术。但是定向问题是一类 NP-hard 问题，为此人们提出了许多启发式算法(如[5-9])。其中文献[5]提出了一种高效的五步启发式算法。近年来，蚁群算法（ACO）[10]已被成功应用于求解诸如 TSP 问题、Job_shop 问题[10,11] 等优化问题。自从蚁群算法提出以来[12]，很多学者对蚁群算法进行了改进[10,11]。其中 Max-Min Ant System (MMAS)通过设定信息素的上下界来避免算法的过早收敛，取得很好的效果[13]。然而在实践中，选取信息素的下界是一个难点.本文采用自适应方法来更新信息素以达到避免停滞的目的。 1本课题得到高等学校博士学科点专项科研基金（项目编号：20050698032）的资助。 - 1 -

http://www.paper.edu.cn 2．利用MMAS求解定向问题 MMAS 是一种广泛应用的蚁群算法。它利用一群受信息素和启发信息引导的蚂蚁构造解用以求解优化问题。其主要流程是：步骤 1：初始化所有边的信息素，设定信息素的上下界等参数。步骤 2：按照路径选择策略构造问题的解。步骤 3：按照信息素更新策略更新信息。步骤 4：判断终止条件是否满足，若满足，算法终止，否则返回到步骤 2。下面在 MMAS 的框架下求解定向问题。首先给出启发信息，再讨论解的构造，最后讨论信息素的更新。 2.1 启发信息在文献[5]中提出了多种表征点的偏好程度的量。考虑到计算复杂性和有效性，本文采用 Tsiligirides[6]提出的量来定义启发信息。假设当前（未完成）路径 P 的最后一个点为i ，对于未选取的点 j ，边( , ) i j 的启发信息定义如下: c ij η = i j ( , ) s j 由上式可知，那些具有较高分数并且离点为i 的距离越小的点，偏好度越高。 (6) 2.2 解的构造为了构造一个解，每只蚂蚁从起点出发，在每一个构造步，它依概率从可选点集中选取一个点，直到可选点集为空，它停止在点 n 。这样就完成一个解的构造过程。假设当前（未完成）路径 P 的最后一个点为i ，路径 P 对应点集为 P%，则可行点集为 = ∈ j V j P L P ∉ { ( % , C i ) + c ij + c jn ≤ T max } )L P 是 P 的长度。其中 ( 蚂蚁的路径选择概率为： ⎧ ⎪ = ⎨ ⎪ ⎩ p ij τ ∑ u C ∈ i 0, i j i j ( , ) ( , ) α β ⋅ η i u i u ( , ) ( , ) α ⋅ η τ , β 如果 j C ∈ i 其他 (7) (8) 2.3 信息素的更新 MMAS 通过限制信息素来避免停滞。并且它把信息素初试化为信息素的上界以使得算法在最初的运行阶段具有较高的探索能力。除此之外，它仅用优解来更新信息素。这个优解 ibs 。在所有蚂蚁都构造完一个解后，信息素按照 gbs 也可能是当代最优解可能是当前最优解以下规则更新: l u v ( , ) τ u v ( , ) τ u v ( , ) l 1 + τ 1 + = ρτ l 1 + < τ > τ u v ( , ) , min , 则则 l + Δ τ u v ( , ) τ u v ( , ) l τ u v ( , ) l 1 + = τ = τ 1 + max min max 如果如果 (9) (10) (11) - 2 -

u vτ ( , )l 其中 u vτ ( , ) Δ 1/ ⎧ = ⎨ 0, ⎩ 其他是边 ( , )u v 在第l 代的信息素。 best f s ( ), 如果 u v ( , ) ∈ s best ; maxτ 和 minτ 分别是信息素的上下 http://www.paper.edu.cn (12) 界。在 MMAS 中, 它们被设定为: τ min 这里 avg 等于 gbs 也可能是当代最优解 / 2n , 优解 n gb f s ( 1) = P best ρ − 1 ((1 ) avg ) (( τ )) max P (1 = − best bestP 是参数。通常选取为 0.05。 ibs 。 − n f x ( ) = n n −∑ ∑∑ s x i ij s i n i 1 = i 1 = j 1 = ) τ max (13) (14) best s 是优解，它可能是当前最 (15) 注意到如果 best f s ( ) 等于 0, 那么最优解必然找到了，算法可终止。因此(14) 是有意义的。 3．两种避免停滞的方法 a , L i {1, a 1 给定两个解 = , a 可知， as 和 , , = 和 L L L b i s b b 1 {1, a n , } k s b n , } l bs 分别由 1k + 和 1l + 条边组成。相应的集合为： k ≤ < l ≤ < , )},1 , )},1 L ), ), L a n ( k b n ( l S a S i j b , 由第二节的构造过程 (16) (17) a 1 b 1 s b ), L L ), ) 1 + a a ( , i i b b , ( j j 1 + S S b = ⊕ a {(1, = {(1, = d s , ( a S I 。 −U b d gg 是距离。 ( , ) S S b a 如上符号，令 S ⊕ = S b a S a , 其中 A 是集合 A 元素个数 , 性质 1: 证明: 给定解 as ， bs 和 cs , 它们相应的边集为 aS , s ≥ ；（2） ( d s ) 0 , a S ) ( ⊕ ⊆ s = 当且仅当 a s ) 0 S d s ( a ⊕U b ) ⊕ S S S S ( ) , b b a b c c , 因此 bS 和 cS 。由 d 的定义可知：（1）。注 d s s ( , a s b = ) ) b s= 。（3） ( d s a s d s s , ) ( , + b c d s ( s c ≤ , , a b ) 。综上所述， d s ( a a b 意到结论成立。 = = ， bs as n {1,3,4, } n {1,2,3,4, } s = 。 ) 3 例 1: 设由距离 d 的定义可知，它可以作为一种两个解差异的度量。在 MMAS 中，由于只增加优解对应边的信息素，因此在信息素更新后，构造优解的概率增加。特别地，当这个概率为 1 时，停滞将会出现，所有的蚂蚁将在下一代构造相同的解。也就是说，下一代构造的解与优解之间的距离为 0。考虑这些构造的解与优解的平均距离 d s ( a , , b 其中 an 是蚂蚁数, best best an i 1 = = ∑ avg s ( d s ( n a is 是第i 只蚂蚁构造的解。 ) - 3 - , i s ) (18)

avg s 特别地，当 ( 采用以下两种方法： best ) 等于 0, 所有的蚂蚁将构造相同的解。为避免这种情况，可以 http://www.paper.edu.cn best avg s 方法 1：如果 ( γ< , 增大 minτ 为 minλτ （ 1λ> ），从而减少信息素的上下界的差距。其中γ和λ是参数。因为这种方法自适应地调整信息素下界，称对应的算法为 AMMAS (adaptive MMAS)。 ) 图 1 AMMAS、 MMAS 和 MMAS+ari 应用到算例64×50的平均距离的演化 Fig1 The evolving of the average distance when AMMAS,MMAS and MMAS+ari are applied to instance 64×50 图 2 AMMAS、 MMAS 和 MMAS+ari 应用到算例64×50的总分数的演化 Fig2 The evolving of the total score when AMMAS,MMAS and MMAS+ari are applied to instance 64×50 γ< , 重新初试化信息素。称对应的算法为 MMAS＋ari (MMAS best avg s 方法 2：如果 ( ) + adaptive reinitializition)。 4．参数设置和数值实验分析本文所提出的算法用 C＋＋实现并且在 P4 1。7GHZ PC 上测试。算例采用文献[5]中的 1α= , 6γ= 。由于 AMMAS 和 MMAS＋ari 能自适应地避免停滞， bestP ibs 。 diamond-shaped 算例集( n 为 64，共 14 个算例)。参数选取为：蚂蚁数 1β= , 可以选取为较大的值，本文取为 0.9。每隔 10 代用算法最大运行代数为 400。对每个算例（记为 n × maxT ），运行 20 次。 gbs 来更新信息素，而在其他代中使用 2λ= , an = 0.95 ρ= , 20 , 图 1 和图 2 显示了三种算法应用到算例 64×50 的结果(这里 n 为 64, maxT 为 50)。图 1 给出了总分数（total score）的变化。图 2 给出了平均距离（average distances）的变化。由图可见，AMMAS 和 MMAS+ari 优于 MMAS。对于 MMAS, 在 180 代后, 平均距离很小(在 2 到 7.9 之间 - 4 -

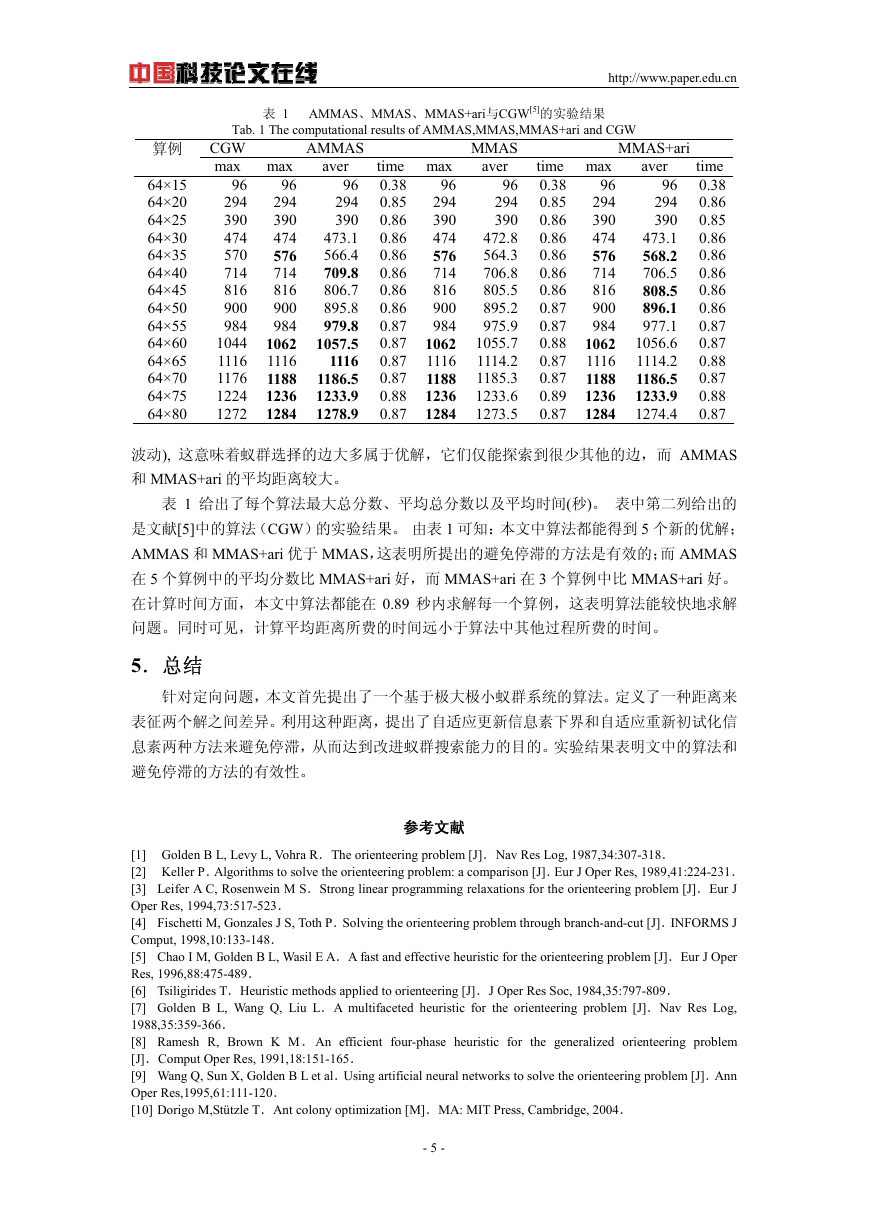
表 1 AMMAS、MMAS、MMAS+ari与CGW[5]的实验结果 Tab. 1 The computational results of AMMAS,MMAS,MMAS+ari and CGW http://www.paper.edu.cn MMAS+ari aver time max 96 96 0.38 294 294 0.85 390 390 0.86 473.1 474 0.86 568.2 576 0.86 706.5 714 0.86 816 808.5 0.86 900 896.1 0.87 984 977.1 0.87 1062 1056.6 0.88 1114.2 1116 0.87 1188 1186.5 0.87 1236 1233.9 0.89 1284 1274.4 0.87 time 0.38 0.86 0.85 0.86 0.86 0.86 0.86 0.86 0.87 0.87 0.88 0.87 0.88 0.87 算例 64×15 64×20 64×25 64×30 64×35 64×40 64×45 64×50 64×55 64×60 64×65 64×70 64×75 64×80 AMMAS CGW max max 96 294 390 474 576 714 816 900 984 aver 96 96 294 294 390 390 474 473.1 570 566.4 714 709.8 816 806.7 900 895.8 984 979.8 1044 1062 1057.5 1116 1116 1116 1176 1188 1186.5 1224 1236 1233.9 1272 1284 1278.9 time max 0.38 96 294 0.85 390 0.86 474 0.86 0.86 576 714 0.86 816 0.86 900 0.86 984 0.87 0.87 1062 1116 0.87 0.87 1188 0.88 1236 0.87 1284 MMAS aver 96 294 390 472.8 564.3 706.8 805.5 895.2 975.9 1055.7 1114.2 1185.3 1233.6 1273.5 波动), 这意味着蚁群选择的边大多属于优解，它们仅能探索到很少其他的边，而 AMMAS 和 MMAS+ari 的平均距离较大。表 1 给出了每个算法最大总分数、平均总分数以及平均时间(秒)。表中第二列给出的是文献[5]中的算法（CGW）的实验结果。由表 1 可知：本文中算法都能得到 5 个新的优解； AMMAS 和 MMAS+ari 优于 MMAS，这表明所提出的避免停滞的方法是有效的；而 AMMAS 在 5 个算例中的平均分数比 MMAS+ari 好，而 MMAS+ari 在 3 个算例中比 MMAS+ari 好。在计算时间方面，本文中算法都能在 0.89 秒内求解每一个算例，这表明算法能较快地求解问题。同时可见，计算平均距离所费的时间远小于算法中其他过程所费的时间。 5．总结针对定向问题，本文首先提出了一个基于极大极小蚁群系统的算法。定义了一种距离来表征两个解之间差异。利用这种距离，提出了自适应更新信息素下界和自适应重新初试化信息素两种方法来避免停滞，从而达到改进蚁群搜索能力的目的。实验结果表明文中的算法和避免停滞的方法的有效性。参考文献 [1] Golden B L, Levy L, Vohra R．The orienteering problem [J]．Nav Res Log, 1987,34:307-318． [2] Keller P．Algorithms to solve the orienteering problem: a comparison [J]．Eur J Oper Res, 1989,41:224-231． [3] Leifer A C, Rosenwein M S．Strong linear programming relaxations for the orienteering problem [J]．Eur J Oper Res, 1994,73:517-523． [4] Fischetti M, Gonzales J S, Toth P．Solving the orienteering problem through branch-and-cut [J]．INFORMS J Comput, 1998,10:133-148． [5] Chao I M, Golden B L, Wasil E A．A fast and effective heuristic for the orienteering problem [J]．Eur J Oper Res, 1996,88:475-489． [6] Tsiligirides T．Heuristic methods applied to orienteering [J]．J Oper Res Soc, 1984,35:797-809． [7] Golden B L, Wang Q, Liu L．A multifaceted heuristic for the orienteering problem [J]．Nav Res Log, 1988,35:359-366． [8] Ramesh R, Brown K M ．An efficient four-phase heuristic for the generalized orienteering problem [J]．Comput Oper Res, 1991,18:151-165． [9] Wang Q, Sun X, Golden B L et al．Using artificial neural networks to solve the orienteering problem [J]．Ann Oper Res,1995,61:111-120． [10] Dorigo M,Stützle T．Ant colony optimization [M]．MA: MIT Press, Cambridge, 2004． - 5 -

[11] Dorigo M, Blum C．Ant colony optimization theory: A survey [J]．Theor Comput Sci, 2005,344:243–278． [12] Dorigo M, Maniezzo V, Colorni A．Ant system: Optimization by a colony of cooperating agents [J]．IEEE Trans Syst, Man, and Cybern.-Part B, 1996,26(1): 29–41． [13] Stützle T, Hoos H H．Max-min ant system [J]．Fut Gener Comput Syst, 2000,16(8):889-914． http://www.paper.edu.cn Solving the orienteering problem by ant colony optimization State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an, Ke Liangjun, Feng Zuren PRC, (710049) Abstract Inspired by max-min ant system, an ant colony optimization algorithm is proposed for the orienteering problem. A distance is proposed to characterize the difference between two solutions. Based on this distance, two methods, that is, adaptively choosing the lower trail limit and reinitializing pheromone trails, are proposed to avoid stagnation. The basic idea is to make the distance between the solutions constructed and the best solution large enough. The experimental results show that: compared with the promising algorithm of Chao et al., the proposed algorithm can quickly obtain high-quality solutions; moreover, the proposed methods can effectively avoid stagnation and improve the search ability of ants. Keywords: Ant Colony Optimization; Orienteering Problem; Distance 作者简介：柯良军，男，1976 年生，博士，主要研究方向是智能优化算法和模式识别；冯祖仁，男，1953 年生，教授，主要研究方向是机器人学，智能计算和模式识别。 - 6 -

分享到：

赞收藏

资料库

论文研究-蚁群算法在定向问题中的应用 .pdf

相关推荐

开发技术

热门标签

最新资料