计算机组成原理课后答案（张功萱）.pdf-资料库

课后答案网，用心为你服务！大学答案 --- 中学答案 --- 考研答案 --- 考试答案最全最多的课后习题参考答案，尽在课后答案网（www.khdaw.com）！ Khdaw团队一直秉承用心为大家服务的宗旨，以关注学生的学习生活为出发点，旨在为广大学生朋友的自主学习提供一个分享和交流的平台。爱校园（www.aixiaoyuan.com）课后答案网（www.khdaw.com）淘答案（www.taodaan.com）

计算机科学与技术学院 07 级学生会学习部作业解答 1.3 冯·诺依曼计算机的基本思想是什么？什么叫存储程序方式？答：冯·诺依曼计算机的基本思想包含三个方面： 1) 计算机由输入设备、输出设备、运算器、存储器和控制器五大部件组成。 2) 采用二进制形式表示数据和指令。 3) 采用存储程序方式。第一章作业解答 khdaw.com 存储程序是指在用计算机解题之前，事先编制好程序，并连同所需的数据预先存入主存储器中。在解题过程（运行程序）中，由控制器按照事先编好并存入存储器中的程序自动地、连续地从存储器中依次取出指令并执行，直到获得所要求的结果为止。 1.4 早期计算机组织结构有什么特点？现代计算机结构为什么以存储器为中心？答：早期计算机组织结构的特点是：以运算器为中心的，其它部件都通过运算器完成信息的传递。随着微电子技术的进步，人们将运算器和控制器两个主要功能部件合二为一，集成到一个芯片里构成了微处理器。同时随着半导体存储器代替磁芯存储器，存储容量成倍地扩大，加上需要计算机处理、加工的信息量与日俱增，以运算器为中心的结构已不能满足计算机发展的需求，甚至会影响计算机的性能。为了适应发展的需要，现代计算机组织结构逐步转变为以存储器为中心。 1.8 衡量计算机性能有哪些基本的技术指标？以你所熟悉的计算机系统为例，说明它的型号、主频、字长、主存容量、所接的 I/O 设备的名称及主要规格。答：衡量计算机性能的基本技术指标主要有： 1. 基本字长 2. 主存容量 3. 运算速度 4. 所配置的外部设备及其性能指标 5. 系统软件的配置还有可靠性、可用性、可维护性、以及安全性、兼容性等性能指标。第二章作业解答 2.2 分别计算用二进制表示 4 位、5 位、8 位十进制数时所需要的最小二进制位的长度。答： ∵ 4 位十进制数的最大数为 9999，213＝8192＜9999＜214＝16384 ∴表示 4 位十进制数所需的最小二进制位的长度为 14 位。 ∵ 5 位十进制数的最大数为 99999，216＝65536＜9999＜217＝131072 ∴表示 5 位十进制数所需的最小二进制位的长度为 17 位。 ∵ 8 位十进制数的最大数为 99999999，226＝67108864＜99999999＜227＝134217728 ∴表示 8 位十进制数所需的最小二进制位的长度为 27 位。根据当 i 位十进制数与 j 位二进制数比较时的等式，10i = 2j，得 j≈3.3i，亦可得到上述结果。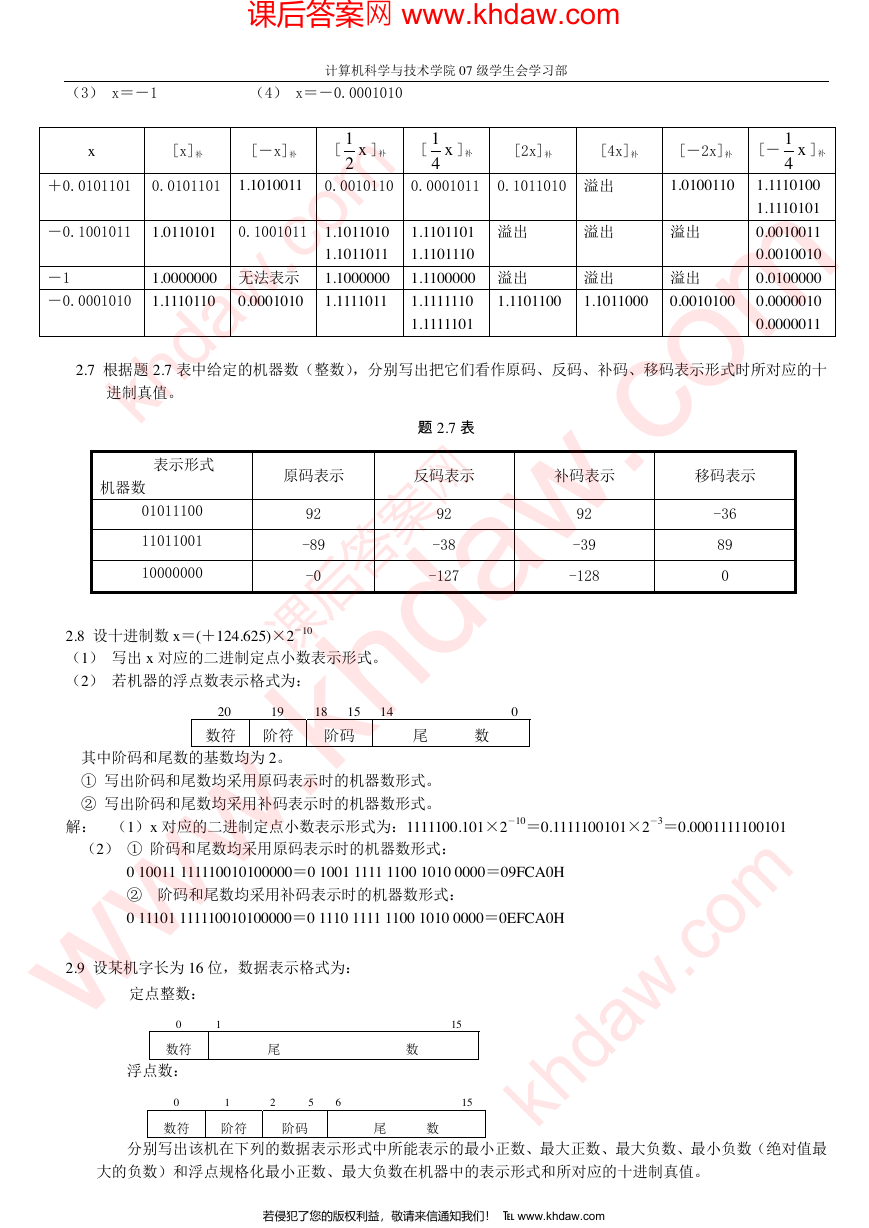 khdaw.com 机器采用定点小数，字长为 8 位，若结果不存在或出错，请注明）（1） x＝＋0.0101101 （2） x＝－0.1001011 2.6 已知 x 的二进制真值，试求 [x]补、[－x]补、[ ]补、[ ]补、[2x]补、[4x]补、[－2x]补、[－ ]补。（设 x21x41x41 www.khdaw.com www.khdaw.com

（3） x＝－1 （4） x＝－0.0001010 计算机科学与技术学院 07 级学生会学习部＋0.0101101 0.0010110 0.0001011 0.1011010 溢出 1.0100110 1.1110100 [ ]补 [ ]补 [2x]补 [4x]补 [－2x]补 [－ ]补 1.1101101 溢出溢出溢出 1.1101110 1.1100000 溢出溢出溢出 1.1110101 0.0010011 0.0010010 0.0100000 1.1111110 1.1101100 1.1011000 0.0010100 0.0000010 1.1111101 0.0000011 x －1 －0.0001010 －0.1001011 1.0110101 0.1001011 1.1011010 [x]补 [－x]补 0.0101101 1.1010011 khdaw.com 1.0000000 无法表示进制真值。 1.1110110 0.0001010 1.1111011 1.1011011 1.1000000 2.7 根据题 2.7 表中给定的机器数（整数），分别写出把它们看作原码、反码、补码、移码表示形式时所对应的十题 2.7 表表示形式机器数 01011100 11011001 10000000 原码表示反码表示补码表示移码表示 92 -89 -0 92 -38 -127 92 -39 -128 -36 89 0 2.8 设十进制数 x＝(＋124.625)×2 （1）写出 x 对应的二进制定点小数表示形式。（2）若机器的浮点数表示格式为：－10 20 19 18 15 14 0 数符阶符阶码尾数解：（1）x 对应的二进制定点小数表示形式为：1111100.101×2 －3＝0.0001111100101 其中阶码和尾数的基数均为 2。 ① 写出阶码和尾数均采用原码表示时的机器数形式。 ② 写出阶码和尾数均采用补码表示时的机器数形式。（2） ① 阶码和尾数均采用原码表示时的机器数形式： 0 10011 111110010100000＝0 1001 1111 1100 1010 0000＝09FCA0H ② 阶码和尾数均采用补码表示时的机器数形式： 0 11101 111110010100000＝0 1110 1111 1100 1010 0000＝0EFCA0H 2.9 设某机字长为 16 位，数据表示格式为：定点整数： 0 1 15 数符浮点数：尾数 0 1 2 5 6 15 数符阶符阶码尾数－10＝0.1111100101×2 khdaw.com 分别写出该机在下列的数据表示形式中所能表示的最小正数、最大正数、最大负数、最小负数（绝对值最大的负数）和浮点规格化最小正数、最大负数在机器中的表示形式和所对应的十进制真值。 x21x41x41 www.khdaw.com www.khdaw.com

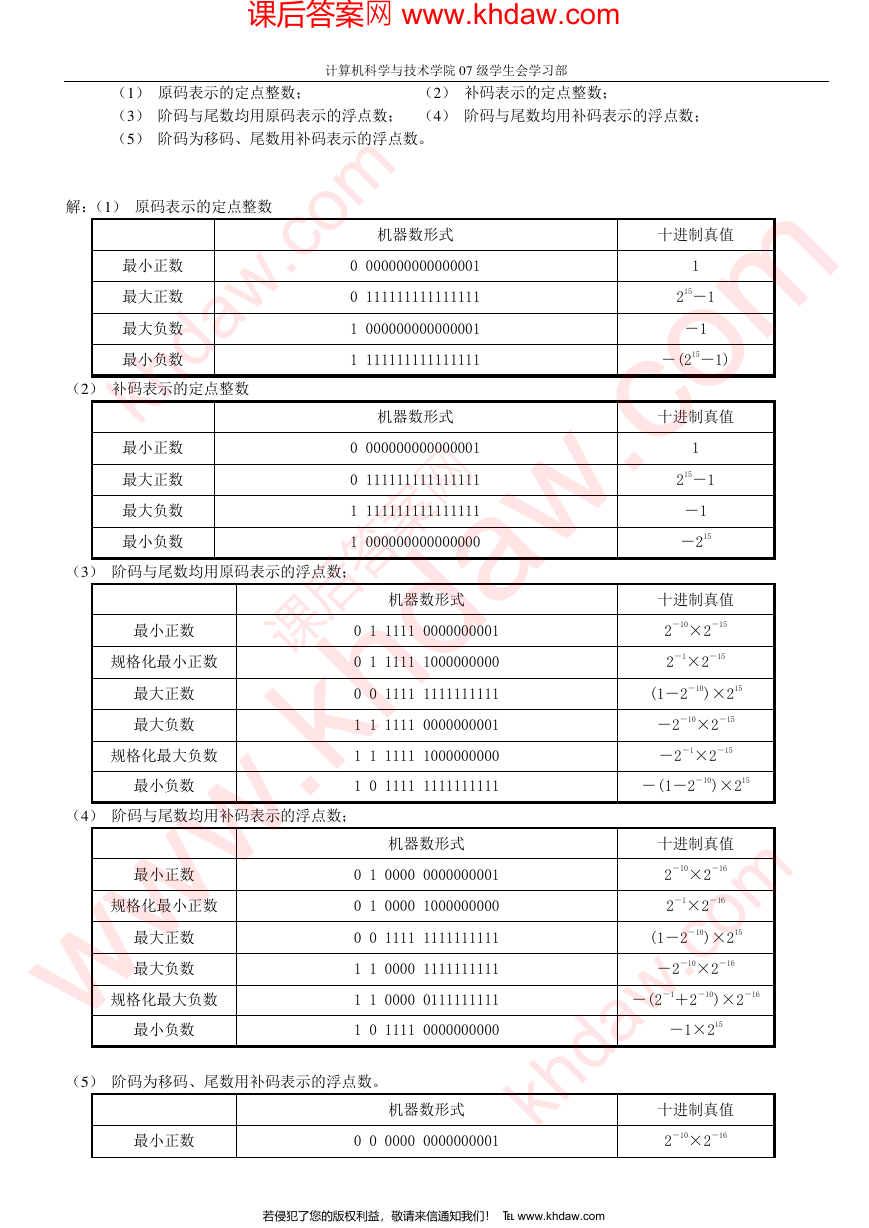
计算机科学与技术学院 07 级学生会学习部（1）原码表示的定点整数；（2）补码表示的定点整数；（3）阶码与尾数均用原码表示的浮点数；（4）阶码与尾数均用补码表示的浮点数；（5）阶码为移码、尾数用补码表示的浮点数。解：（1）原码表示的定点整数最小正数 khdaw.com 最大正数最大负数最小负数（2）补码表示的定点整数机器数形式十进制真值 0 000000000000001 0 111111111111111 1 000000000000001 1 111111111111111 1 215－1 －1 －(215－1) 机器数形式十进制真值最小正数最大正数最大负数最小负数 0 000000000000001 0 111111111111111 1 111111111111111 1 000000000000000 （3）阶码与尾数均用原码表示的浮点数；最小正数机器数形式 0 1 1111 0000000001 规格化最小正数 0 1 1111 1000000000 最大正数最大负数 0 0 1111 1111111111 1 1 1111 0000000001 规格化最大负数 1 1 1111 1000000000 1 215－1 －1 －215 十进制真值 2－10×2－15 2－1×2－15 (1－2－10)×215 －2－10×2－15 －2－1×2－15 最小负数 1 0 1111 1111111111 －(1－2－10)×215 （4）阶码与尾数均用补码表示的浮点数；最小正数规格化最小正数最大正数最大负数规格化最大负数最小负数机器数形式 0 1 0000 0000000001 0 1 0000 1000000000 0 0 1111 1111111111 1 1 0000 1111111111 1 1 0000 0111111111 1 0 1111 0000000000 2－1×2－16 2－10×2－16 十进制真值 (1－2－10)×215 khdaw.com －(2－1＋2－10)×2－16 －2－10×2－16 十进制真值－1×215 2－10×2－16 （5）阶码为移码、尾数用补码表示的浮点数。最小正数机器数形式 0 0 0000 0000000001 www.khdaw.com www.khdaw.com

0 1 1111 1111111111 1 0 0000 1111111111 1 0 0000 0111111111 1 0 1111 0000000000 2－1×2－16 (1－2－10)×215 －2－10×2－16 －(2－1＋2－10)×2－16 －1×215 2.11 用十六进制写出下列十进制数的 IEEE754 标准 32 位单精度浮点数的机器数的表示形式。（1） 0.15625 （2）－0.15625 （3） 16 （4）－5 规格化最小正数 0 0 0000 1000000000 计算机科学与技术学院 07 级学生会学习部－3 最小负数最大正数最大负数规格化最大负数 khdaw.com 解：（1）(0.15625)10＝(0. 00101)2＝1.01×2 阶码 E＝127＋(－3)＝124＝(1111100)2＝01111100 机器数形式：0 01111100 01000000000000000000000 十六进制形式：3E200000H －3 （2） (－0.15625)10＝(－0. 00101)2＝－1.01×2 阶码 E＝127＋(－3)＝124＝(1111100)2＝01111100 机器数形式：1 01111100 01000000000000000000000 十六进制形式：BE200000H （3） (16)10＝(10000)2＝－1.0000×24 阶码 E＝127＋4＝131＝(10000011)2 机器数形式：0 10000011 00000000000000000000000 十六进制形式：41800000H （4） (－5)10＝(－101)2＝－1.01×22 阶码 E＝127＋2＝129＝(10000001)2 机器数形式：1 10000001 01000000000000000000000 十六进制形式：C0A00000H 2.13 写出下列十六进制的 IEEE 单精度浮点数代码所代表的十进制数值。（1） 42E48000 （2） 3F880000 （3） 00800000 （4） C7F00000 解：（1） 42E48000＝0 10000101 11001001000000000000000 指数＝(10000101)2－127＝133－127＝6 M＝1.11001001000000000000000＝1＋(1/2＋1/4＋1/32＋1/256) 十进制数值 N＝[1＋(1/2＋1/4＋1/32＋1/256)]×26＝114.25 （2） 3F880000＝0 01111111 00010000000000000000000 指数＝(01111111)2－127＝127－127＝0 M＝1.00010000000000000000000＝1＋1/16＝1.0625 十进制数值 N＝1.0625×20＝1.0625 （3） 00800000＝0 00000001 00000000000000000000000 指数＝(00000001)2－127＝1－127＝－126 M＝1.00000000000000000000000 十进制数值 N＝1×2 （4） C7F00000＝1 10001111 11100000000000000000000 指数＝(10001111)2－127＝143－127＝16 M＝1. 11100000000000000000000＝1＋(1/2＋1/4＋1/8)＝1.875 十进制数值 N＝－(216＋215＋214＋213)＝－15×213＝－122880＝－1.875×216 khdaw.com －126 www.khdaw.com www.khdaw.com

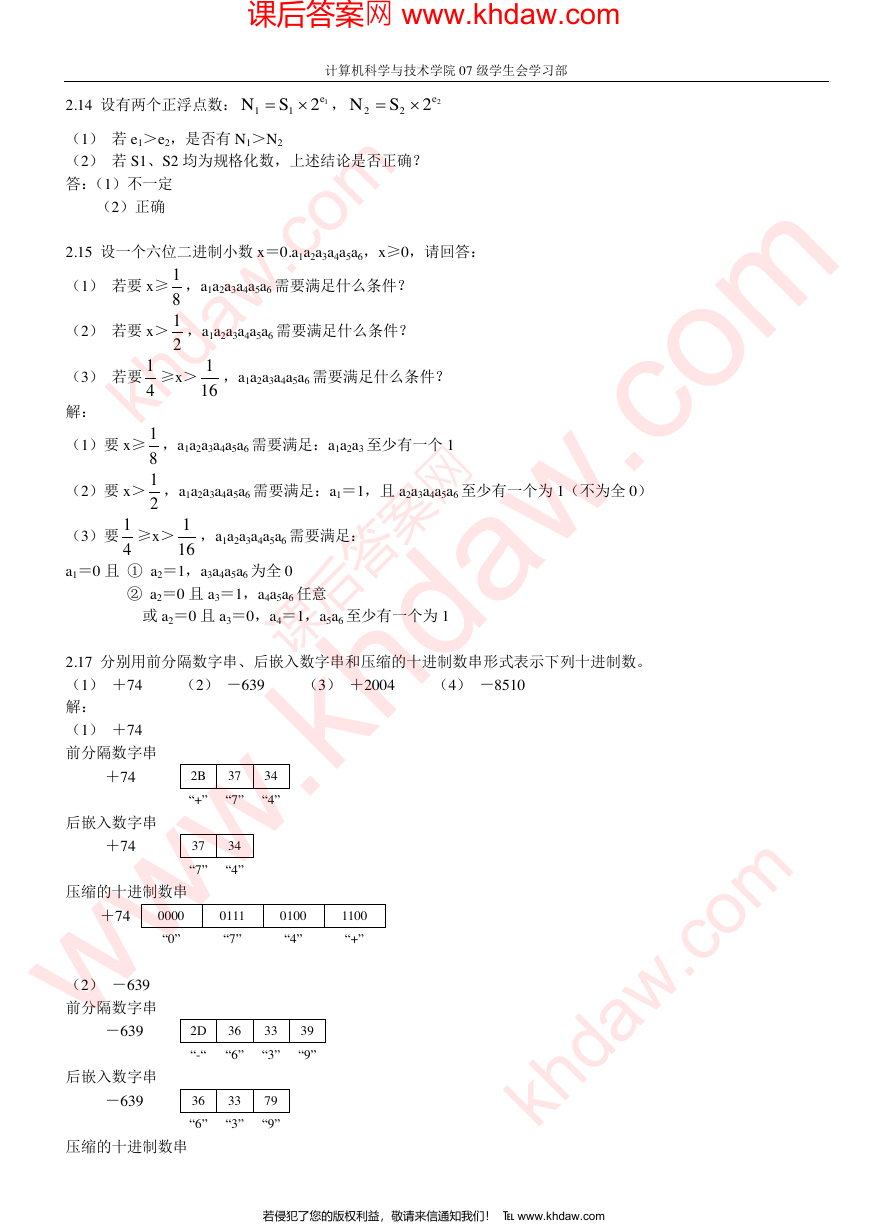
计算机科学与技术学院 07 级学生会学习部 2.14 设有两个正浮点数：， 2.15 设一个六位二进制小数 x＝0.a1a2a3a4a5a6，x≥0，请回答：（1）若要 x≥ ，a1a2a3a4a5a6 需要满足什么条件？（1）若 e1＞e2，是否有 N1＞N2 （2）若 S1、S2 均为规格化数，上述结论是否正确？答：（1）不一定（2）正确 khdaw.com （2）若要 x＞，a1a2a3a4a5a6 需要满足什么条件？（3）若要 ≥x＞，a1a2a3a4a5a6 需要满足什么条件？解：（1）要 x≥ ，a1a2a3a4a5a6 需要满足：a1a2a3 至少有一个 1 （2）要 x＞，a1a2a3a4a5a6 需要满足：a1＝1，且 a2a3a4a5a6 至少有一个为 1（不为全 0）（3）要 ≥x＞，a1a2a3a4a5a6 需要满足： a1＝0 且 ① a2＝1，a3a4a5a6 为全 0 ② a2＝0 且 a3＝1，a4a5a6 任意或 a2＝0 且 a3＝0，a4＝1，a5a6 至少有一个为 1 2.17 分别用前分隔数字串、后嵌入数字串和压缩的十进制数串形式表示下列十进制数。（1）＋74 （2）－639 （3）＋2004 （4）－8510 解：（1）＋74 前分隔数字串＋74 2B 37 34 “+” “7” “4” 后嵌入数字串＋74 37 34 “7” “4” 压缩的十进制数串＋74 0000 0111 0100 1100 “0” “7” “4” “+” （2）－639 前分隔数字串－639 2D 36 33 39 “-“ “6” “3” “9” 后嵌入数字串－639 36 33 79 “6” “3” “9” 压缩的十进制数串 khdaw.com 1e112SN2e222SN812141161812141161 www.khdaw.com www.khdaw.com

－639 0110 0011 1001 1101 计算机科学与技术学院 07 级学生会学习部（3）＋2004 前分隔数字串＋2004 后嵌入数字串＋2004 “-” 34 “9” 30 30 “3” 32 30 2B 32 “6” “0” “0” “4” “+” “2” khdaw.com 0010 0000 “2” “0” “0” “4” 0000 ＋2004 30 34 “0” “2” “0” 2D 38 35 31 30 （4）－8510 前分隔数字串－8510 压缩的十进制数串 0000 0100 1100 “0” “4” “+” “-“ “8” “5” “1” “0” 后嵌入数字串－8510 38 35 31 70 “8” “5” “1” “0” 压缩的十进制数串－8510 0000 1000 0101 0001 0000 1101 “0” “8” “5” “1” “0” “-” 2.19 什么是“码距”？数据校验与码距有什么关系？答：码距是指在一组编码中任何两个编码之间最小的距离。数据校验码的校验位越多，码距越大，编码的检错和纠错能力越强。 2.21 下面是两个字符（ASCII 码）的检一纠一错的海明校验码（偶校验），请检测它们是否有错？如果有错请加以改正，并写出相应的正确 ASCII 码所代表的字符。（1） 10111010011 （2） 10001010110 解：（1）指误字为 E1＝P1⊕A6⊕A5⊕A3⊕A2⊕A0＝1⊕1⊕1⊕1⊕0⊕1＝1 E2＝P2⊕A6⊕A4⊕A3⊕A1⊕A0＝0⊕1⊕0⊕1⊕1⊕1＝0 E3＝P4⊕A5⊕A4⊕A3＝1⊕1⊕0⊕1＝1 E4＝P8⊕A2⊕A1⊕A0＝0⊕0⊕1⊕1＝0 得到的指误字为 E4E3E2E1＝0101＝(5)10，表示接收到的海明校验码中第 5 位上的数码出现了错误。将第 5 位上的数码 A5＝1 取反，即可得到正确结果 10110010011。正确 ASCII 码所代表的字符为 1001011＝“K”。（2）指误字为 khdaw.com E1＝P1⊕A6⊕A5⊕A3⊕A2⊕A0＝1⊕0⊕1⊕1⊕1⊕0＝0 E2＝P2⊕A6⊕A4⊕A3⊕A1⊕A0＝0⊕0⊕0⊕1⊕1⊕0＝0 E3＝P4⊕A5⊕A4⊕A3＝0⊕1⊕0⊕1＝0 E4＝P8⊕A2⊕A1⊕A0＝0⊕1⊕1⊕0＝0 得到的指误字为 E4E3E2E1＝0000，无错。正确 ASCII 码为 0101110＝“．” 2.22 试编出 8 位有效信息 01101101 的检二纠一错的海明校验码（用偶校验）。 www.khdaw.com www.khdaw.com

解：8 位有效信息需要用 4 个校验位，所以检一纠一错的海明校验码共有 12 位。 4 个校验位为：计算机科学与技术学院 07 级学生会学习部 P1＝A7⊕A6⊕A4⊕A3⊕A1＝0⊕1⊕0⊕1⊕0＝0 P2＝A7⊕A5⊕A4⊕A2⊕A1＝0⊕1⊕0⊕1⊕0＝0 P4＝A6⊕A5⊕A4⊕A0＝1⊕1⊕0⊕1＝1 P8＝A3⊕A2⊕A1⊕A0＝1⊕1⊕0⊕1＝1 检一纠一错的海明校验码：000111011101＝1DDH 检二纠一错的海明校验码，增加 P0 khdaw.com 101011001000111110011 P0＝P1⊕P2⊕A7⊕P4⊕A6⊕A5⊕A4⊕P8⊕A3⊕A2⊕A1⊕A0＝1 有效信息 01101101 的 13 位检二纠一错的海明校验码：1000111011101＝11DDH 2.23 设准备传送的数据块信息是 1010110010001111，选择生成多项式为 G(x)＝100101，试求出数据块的 CRC 码。解：模 2 除后，余数 R(x)＝10011，数据块的 CRC 码： 2.24 某 CRC 码（CRC）的生成多项式 G(x)＝x3＋x2＋1，请判断下列 CRC 码是否存在错误。（1） 0000000 （2） 1111101 （3） 1001111 （4） 1000110 解：G(x)＝1101 （1） 0000000 模 2 除 1101，余数为：000，无错（2） 1111101 模 2 除 1101，余数为：010，有错（3） 1001111 模 2 除 1101，余数为：100，有错（4） 1000110 模 2 除 1101，余数为：000，无错第三章作业解答作业三 (1) 3.1 已知[x]补、[y]补，计算[x＋y]补和[x－y]补，并判断溢出情况。（1） [x] 补＝0.11011 [y]补＝0.00011 （2） [x]补＝0.10111 [y]补＝1.00101 （3） [x] 补＝1.01010 [y]补＝1.10001 解：（1） [x]补＝0.11011 [y]补＝0.00011 [－y]补＝1.111101 [x＋y]补＝0.11011＋0.00011＝0.11110 [x－y]补＝0.11011＋1.111101＝0.11000 （2）[x]补＝0.10111 [y]补＝1.00101 [－y]补＝0.11011 [x＋y]补＝0.10111＋1.00101＝1.11100 [x－y]补＝0.10111＋0.11011＝1.10010 溢出（3）[x]补＝1.01010 [y]补＝1.10001 [－y]补＝0.01111 [x＋y]补＝1.01010＋1.10001＝0.11011 溢出 [x－y]补＝1.01010＋0.01111＝1.11001 3.2 已知[x]补、[y]补，计算[x＋y]变形补和[x－y]变形补，并判断溢出情况。（1） [x]补＝100111 [y]补＝111100 （2） [x]补＝011011 [y]补＝110100 （3） [x]补＝101111 [y]补＝011000 解：（1）[x]变形补＝1100111 [y]变形补＝1111100 [－y]变形补＝0000100 [x＋y]变形补＝1100111＋1111100＝1100011 [x－y]变形补＝1100111＋0000100＝1101011 （2）[x]变形补＝0011011 [y]变形补＝1110100 [－y] ]变形补＝0001100 khdaw.com www.khdaw.com www.khdaw.com

资料库

计算机组成原理课后答案（张功萱）.pdf

相关推荐

课程资源

热门标签

最新资料