数字集成电路设计第五章答案 chapter5_ex

YoArcher-3161918-4744302543352693101.pdf-第1页.png

第1页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第2页.png

第2页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第3页.png

第3页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第4页.png

第4页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第5页.png

第5页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第6页.png

第6页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第7页.png

第7页 / 共27页

YoArcher-3161918-4744302543352693101.pdf-第8页.png

第8页 / 共27页

C H A P T E R 5 T H E C M O S I N V E R T E R Quantification of integrity, performance, and energy metrics of an inverter Optimization of an inverter design 5.1 Exercises and Design Problems 5.4.2 Propagation Delay: First-Order 5.2 The Static CMOS Inverter — An Intuitive Perspective 5.3 Evaluating the Robustness of the CMOS Inverter: The Static Behavior 5.3.1 Switching Threshold 5.3.2 Noise Margins 5.3.3 Robustness Revisited 5.4 Performance of CMOS Inverter: The Dynamic Behavior 5.4.1 Computing the Capacitances Analysis 5.4.3 Propagation Delay from a Design Perspective 5.5 Power, Energy, and Energy-Delay 5.5.1 Dynamic Power Consumption 5.5.2 Static Consumption 5.5.3 Putting It All Together 5.5.4 Analyzing Power Consumption Using SPICE 5.6 Perspective: Technology Scaling and its Impact on the Inverter Metrics 180

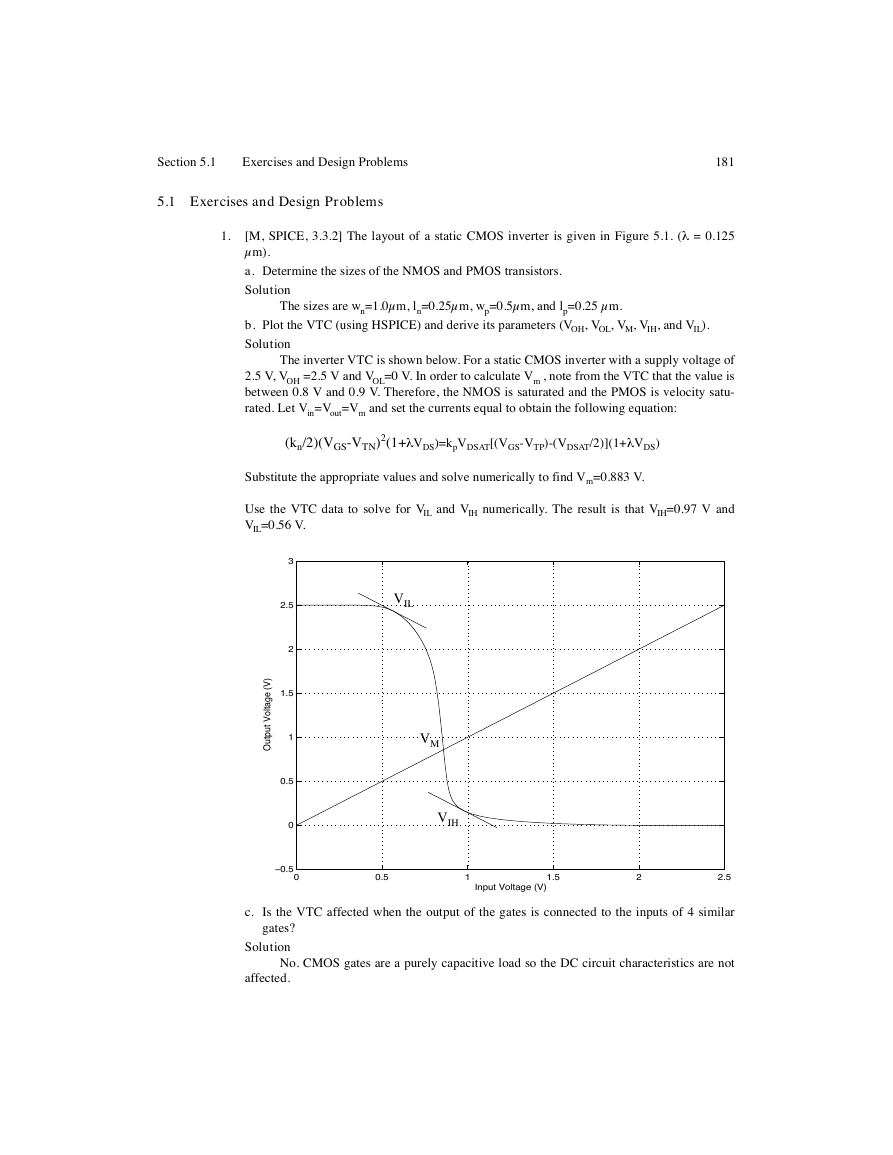
Section 5.1 Exercises and Design Problems 181 5.1 Exercises and Design Problems 1. [M, SPICE, 3.3.2] The layout of a static CMOS inverter is given in Figure 5.1. (λ = 0.125 µm). a. Determine the sizes of the NMOS and PMOS transistors. Solution The sizes are wn=1.0µm, ln=0.25µm, wp=0.5µm, and lp=0.25 µm. b. Plot the VTC (using HSPICE) and derive its parameters (VOH, VOL, VM, VIH, and VIL). Solution The inverter VTC is shown below. For a static CMOS inverter with a supply voltage of 2.5 V, VOH =2.5 V and VOL=0 V. In order to calculate Vm , note from the VTC that the value is between 0.8 V and 0.9 V. Therefore, the NMOS is saturated and the PMOS is velocity satu- rated. Let Vin=Vout=Vm and set the currents equal to obtain the following equation: (kn/2)(VGS-VTN)2(1+λVDS)=kpVDSAT[(VGS-VTP)-(VDSAT/2)](1+λVDS) Substitute the appropriate values and solve numerically to find Vm=0.883 V. Use the VTC data to solve for VIL and VIH numerically. The result is that VIH=0.97 V and VIL=0.56 V. ) V ( e g a t l o V t u p t u O 3 2.5 2 1.5 1 0.5 0 −0.5 0 VIL VM VIH 0.5 1 1.5 2 2.5 Input Voltage (V) c. Is the VTC affected when the output of the gates is connected to the inputs of 4 similar gates? Solution No. CMOS gates are a purely capacitive load so the DC circuit characteristics are not affected.

182 THE CMOS INVERTER Chapter 5 GND Poly In λ 2 NMOS Poly Metal1 Out Metal1 VDD = 2.5 V. PMOS Figure 5.1 CMOS inverter layout. d. Resize the inverter to achieve a switching threshold of approximately 0.75 V. Do not lay- out the new inverter, use HSPICE for your simulations. How are the noise margins affected by this modification? Solution Changing the NMOS sizing to wn=2.0µm moves the switching threshold to 0.75 V. This increases NMH and decreases NML. 2. Figure 5.2 shows a piecewise linear approximation for the VTC. The transition region is approximated by a straight line with a slope equal to the inverter gain at VM. The intersection of this line with the VOH and the VOL lines defines VIH and VIL. a. The noise margins of a CMOS inverter are highly dependent on the sizing ratio, r = kp/kn, of the NMOS and PMOS transistors. Use HSPICE with VTn = |VTp| to determine the value of r that results in equal noise margins? Give a qualitative explanation. Solution The TSMC 0.25µm models were used for simulation and the threshold voltages of NMOS and PMOS devices are nearly equal in this process. A value near r=1 should result in equal noise margins, since the transistors will be closely matched. HSPICE showed that the resulting noise margins for this sizing were NMH=0.97 V and NML=1.1 V. The mismatch is due to the fact that the PMOS threshold voltage is actually slightly lower, so the PMOS is stronger and the upper noise margin is reduced. The actual value that results in equal noise margins is r=0.83. b. Section 5.3.2 of the text uses this piecewise linear approximation to derive simplified expressions for NMH and NML in terms of the inverter gain. The derivation of the gain is based on the assumption that both the NMOS and the PMOS devices are velocity saturated at VM . For what range of r is this assumption valid? What is the resulting range of VM ? Solution

Section 5.1 Exercises and Design Problems 183 Using the equations for finding the region of operation, it can be shown that the PMOS and NMOS are both velocity saturated only while the switching threshold is between 1.06 V and 1.10 V. Since this range may be considered inclusive, we can assume that both devices are velocity saturated and set the currents equal with VIN=VOUT=VM to find kp/kn . The result is that kp/kn must be between 0.34 and 0.41. This result can be checked by sizing the devices accordingly and testing the resulting VM in HSPICE. The result gives a range of 1.04 V to 1.09 V. This makes sense, because the NMOS must be much stronger than the PMOS to achieve a switching threshold near 1 V. c. Derive expressions for the inverter gain at VM for the cases when the sizing ratio is just above and just below the limits of the range where both devices are velocity saturated. What are the operating regions of the NMOS and the PMOS for each case? Consider the effect of channel-length modulation by using the following expression for the small-signal resistance in the saturation region: ro,sat = 1/(λID). Vout VOH VOL Solution: VM VIL VIH Vin Figure 5.2 A different approach to derive VIL and VIH. When VM is slightly larger than 1.1 V, the NMOS is velocity saturated and the PMOS is saturated. When V‘ is slightly smaller than 1.06 V, the PMOS is velocity saturated and the NMOS is saturated. Section 5.3.2 of the text shows this derivation for the case when both devices are velocity saturated. These derivations can be completed by substituting the correct current equations and using the same method. The results are as follows: For the case when the NMOS is saturated and the PMOS is velocity saturated: dVout --------------- dVin –= – ) 1 λ +( ( ( ) – kn Vin Vtn p Vout VDD ------------------------------------------------------------------------------------------------------------------------------------------------------------------------ λ VDSATP kn  ----------------------- ------------ Vin Vtn  2 +( kpVDSATP 1 λ λ  p Vin VDD  kpVDSATP nVout Vtp )2 + + – – – 2 – n ) ) ( Dropping the second order terms in the numerator, substituting Vm for Vin, and simplifying the denominator leads to the following expression for the gain: dVout --------------- dVin –= kn Vm Vtn kpVDSATP ----------------------------------------------------------------------- λ p– ID Vm n – ( ) ( ) + ) λ ( For the case when the NMOS is velocity saturated and the PMOS is saturated: dVout --------------- dVin –= ) ) ) +( knVDSATN 1 λ --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- λ ( p Vout VDD )2 kp Vin VDD VDSATN  ------------------------  – Vtp λ kp p ------------ Vin VDD 2 nVout  n Vin Vtn  knVDSATN ) 1 λ +( Vtp + + – – – 2 – – – ( (

184 THE CMOS INVERTER Chapter 5 Again, dropping the second order terms in the numerator, substituting Vm for Vin, and simpli- fying the denominator leads to the following expression for the gain: dVout --------------- dVin –= ) knVDSATN kp Vm VDD Vtp ------------------------------------------------------------------------------------------ + – – λ p– ) ( ) λ ( n ( ID Vm 3. [M, SPICE, 3.3.2] Figure 5.3 shows an NMOS inverter with a resistive load. a. Qualitatively discuss why this circuit behaves as an inverter. Solution For VIN VT, M1 is con- ducting and Vout=2.5V - (I*R). This in turn gives a low Vout and the input signal is inverted. b. Find VOH and VOL calculate VIH and VIL. Solution Assuming negligable leakage, when Vin

Section 5.1 Exercises and Design Problems 185 * problem 3 for solutions 2.6 2.4 2.2 2 1.8 1.6 1.4 1.2 1 800m 600m 400m 200m 0 ) n i l ( s e g a t l o V 0 2n 4n 6n Time (lin) (TIME) 8n 10n d. 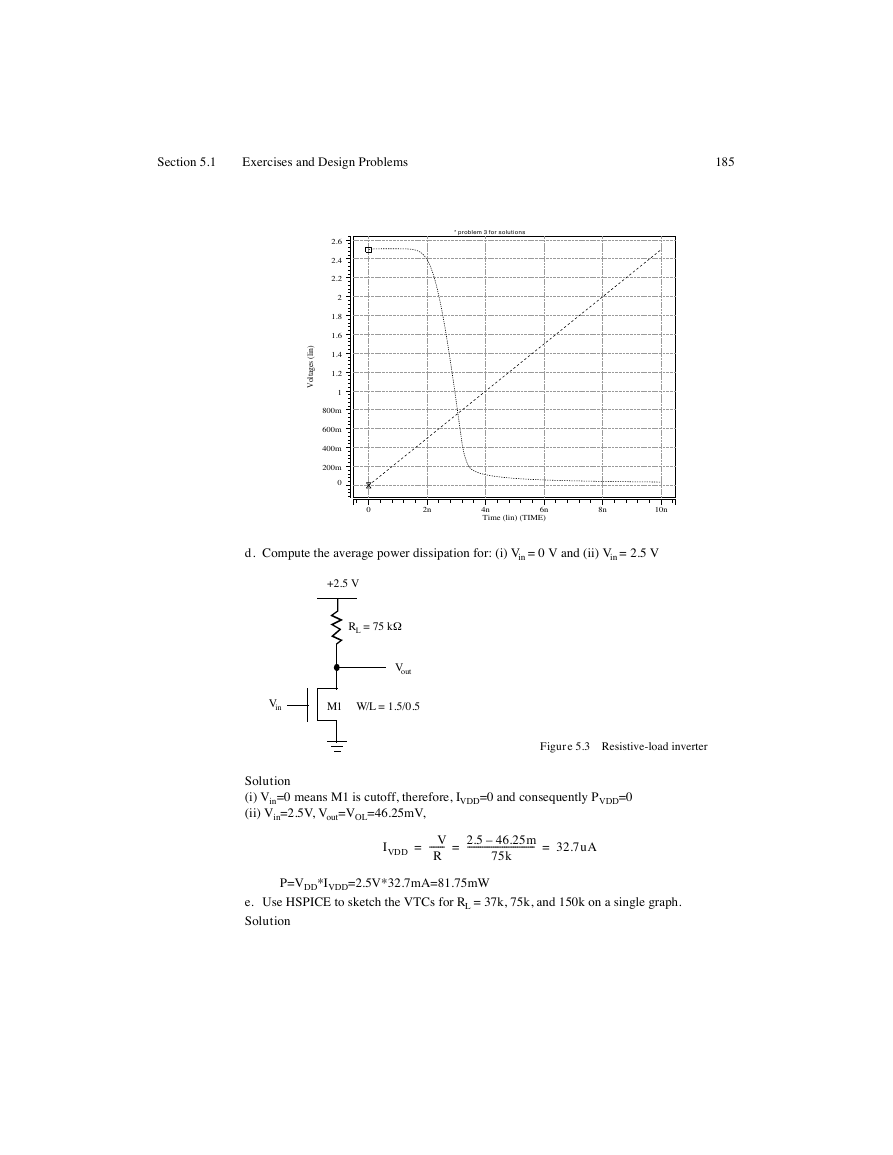Compute the average power dissipation for: (i) Vin = 0 V and (ii) Vin = 2.5 V +2.5 V RL = 75 kΩ Vout Vin M1 W/L = 1.5/0.5 Figure 5.3 Resistive-load inverter Solution (i) Vin=0 means M1 is cutoff, therefore, IVDD=0 and consequently PVDD=0 (ii) Vin=2.5V, Vout=VOL=46.25mV, IVDD = ∆V ------- R = 2.5 – 46.25m ------------------------------- 75k = 32.7uA P=VDD*IVDD=2.5V*32.7mA=81.75mW e. Use HSPICE to sketch the VTCs for RL = 37k, 75k, and 150k on a single graph. Solution

186 THE CMOS INVERTER Chapter 5 2.6 2.4 2.2 2 1.8 1.6 1.4 1.2 1 800m 600m 400m 200m 0 ) n i l ( s e g a t l o V * problem 5.3e R=150k R=75k R=37k 0 500m 1 1.5 Voltage X (lin) (VOLTS) 2 2.5 f. Comment on the relationship between the critical VTC voltages (i.e., VOL, VOH, VIL, VIH) and the load resistance, RL. Solution As RL increases, the VTC curve becomes more ideal for the following reasons: VOL decreases, NML increases, VIH decreases, and NMH increases. However, these come as tradeoffs because, as RL increases, VIL decreases, which is less ideal, and VOH remains unchanged. g. Do high or low impedance loads seem to produce more ideal inverter characteristics? Solution As the impedance load increases, there is a tradeoff, the inverter VTC becomes more ideal with a higher gain and thus better noise margins. However, the VTC curve is shifted in favor of M1 and the threshold voltage is lowered as the VTC moves to the left. [E, None, 3.3.3] For the inverter of Figure 5.3 and an output load of 3 pF: a. Calculate tplh, tphl, and tp. Solution tpLH=0.69RLCL= 155 nsec. 4. For tpHL: First calculate Ron for Vout at 2.5V and 1.25V. At Vout=2.5V, IDVsat=0.439mA giving Ron= 5695Ω and when Vout=1.25V, IDvsat=0.41m giving Ron= 3049W. Thus, the average resistance between Vout=2.5Vand Vout=1.25V is Raverage=4.372kΩ. tpLH=0.69RaverageCL=9.05nsec. tp=av{tpLH, tpHL}=82.0nsec b. Are the rising and falling delays equal? Why or why not? Solution tpLH >> tpHL because RL=75kΩ is much larger than the effective linearized on-resis- tance of M1.

Section 5.1 Exercises and Design Problems 187 c. Compute the static and dynamic power dissipation assuming the gate is clocked as fast as possible. Solution Static Power: VIN=VOL gives Vout=VOH=2.5V, thus IVDD=0A so PVDD=0W. VIN=VOH gives Vout=VOL=46.3mV, which is in the linear region. Calculating the current through M1 gives IVDD=32.8mA --> PVDD=82mW Dynamic Power: Pdyn=CL ∆V*Vdd*fmax=3pF*(2.5V-46.3mV)*2.5V*12.2MHz=0.225mW. 5. The next figure shows two implementations of MOS inverters. The first inverter uses only NMOS transistors. a. Calculate VOH, VOL, VM for each case. VDD = 2.5V M2 W/L=0.375/0.25 VOUT VIN VIN M1 W/L=0.75/0.25 A Figure 5.4 Inverter Implementations VDD = 2.5V W/L=0.75/0.25 VOUT W/L=0.375/0.25 M4 M3 B Solution Circuit A. VOH: We calculate VOH, when M1 is off. The threshold for M2 is: VT = VT0 γ ⋅+ ( 2φ – + VSB F – 2φ F– ) , VSB = VOUT , 2φ F– = 0.6V and M2 will be off when: VT– Substitute VT in the last equation and solve for VOUT. VDD VOUT – VGS VT– = = 0 , VDD VOUT – VT– = – 2.5 VOUT – ( 0.43 + 0.4 ⋅ ( + 0.6 VOUT – ) ) 0.6 = 0 We get VOUT=VOH=1.765V VOL: To calculate VOL, we set VIN=VDD=2.5V. We expect VOUT to be low, so we can make the assumption that M2 will be velocity saturated and M1 will be in the linear region. For M2: ID2 = k'n ⋅ ⋅ W2 -------- L2 (     VGS VT– ⋅ ) VDSAT – 2  VDSAT  -------------------   2 ⋅ 1 λVDS +( ) and

资料库

数字集成电路设计第五章答案 chapter5_ex_sol.pdf

相关推荐

课程资源

热门标签

最新资料