盘式制动器热应力场仿真分析王哲（开滦能源化工股份有限公司吕家坨矿业分公司，河北唐山063000）摘要：为了有效检测盘式制动器的性能，利用ANSYS建立了盘式制动器热应力三维有限元分析模型，探讨其在摩擦副作用下热应力分布的特点和规律，为优化盘式制动器的性能提供一些参考。关键词：盘式制动器；热应力；ANSYS中图分类号：TD534+.5文献标识码：A文章编号：2095-5979（2013）06-0008-03DiscBrakeThermalStressFieldSimulationAnalysisWANGZhe(LyujiatuoMine,KailuanEnergyChemicalCorporationLtd.,Tangshan063000,China)Abstract：Inordertoeffectivelydetecttheperformanceofthediscbrake,whichwasestablishedbasedonANSYSthree-dimensionalfiniteelementanalysismodelofthermalstress,thecharacteristicsofthethermalstressdistributionunderthefrictioneffectsandlawswerediscussed,somereferencesforoptimizingtheperformanceofdiscbrakewasprovided.Keywords：discbrake;thermalstress;ANSYS收稿日期：2013-08-21；责任编辑：聂明勋作者简介：王哲（1985—），男，河北廊坊人，助理工程师。E-mail：666999.chen@163.com0引言盘式制动器是一种常用的制动装置，广泛应用于交通运输、矿山开采等领域，同时，它也是一种经济、高效的扭矩加载装置，随着盘式制动器应用领域的扩展，国内外学者针对其工作性能也进行了大量的研究和探索。制动器制动产生摩擦热，如果热应力的数值超过了摩擦材料的强度极限，则易使其表面产生裂纹，如果热应力超过了摩擦材料的屈服极限，将导致其产生热变形，所以应对摩擦热产生的应力场进行分析研究，了解其特点和规律，为盘式制动器的性能优化提供参考。1三维热应力分析概述ANSYS软件具有强大的耦合场仿真功能，在温度场-结构场联合仿真中多采用顺序耦合的方法，即温度场仿真采用热单元分析建模，得到稳态或者瞬态的温度场仿真数据，分析结果存储于.RTH文件，然后将热单元转换成对应的结构单元，读入前面得到的温度结果文件，利用内部程序计算相应时刻的热应力，得到.RST结果文件，采用单元转换的方法将前面得到的温度场结果按时间顺序导入结果文件，计算出相应的热应力分布结果。ANSYS接触分析中，若按照接触类型的不同，可以分为柔体-柔体接触、刚体-柔体接触；若按照接触形式的不同，可以分为点-点接触、线-线接触、面-面接触等。盘式制动器在加载过程中，摩擦片在不同时刻分别与摩擦盘的不同位置接触，摩擦片和摩擦盘的接触变形、应力分布，为了真实地模拟接触的过程，需要将摩擦片与摩擦盘当做柔体处理，同时采用面-面接触类型进行仿真分析。2柔体-柔体接触分析的特点ANSYS默认采用线性方程求解系统响应的问题，然而由于整个接触系统的“未知性”，大多数的线性计算都需要在不断校正的基础上进行，这种矫正方法就是将载荷分成若干载荷步以及他们的子步，然后依次计算，每一步新的计算都建立在已有问题探讨CoalandChemicalIndustry煤炭与化工第36卷第6期2013年10月Vol.36No.6Oct.20138

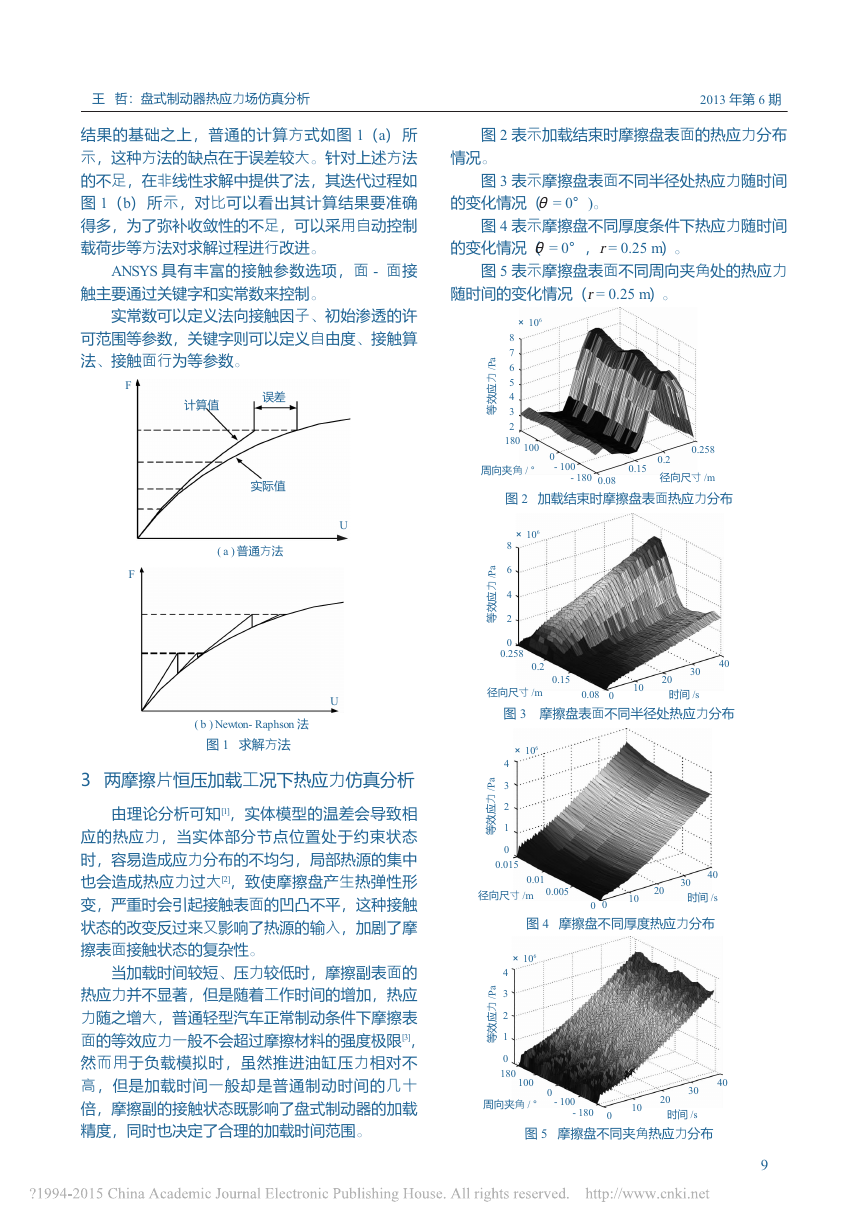
2013年第6期图5摩擦盘不同夹角热应力分布结果的基础之上，普通的计算方式如图1（a）所示，这种方法的缺点在于误差较大。针对上述方法的不足，在非线性求解中提供了法，其迭代过程如图1（b）所示，对比可以看出其计算结果要准确得多，为了弥补收敛性的不足，可以采用自动控制载荷步等方法对求解过程进行改进。ANSYS具有丰富的接触参数选项，面-面接触主要通过关键字和实常数来控制。实常数可以定义法向接触因子、初始渗透的许可范围等参数，关键字则可以定义自由度、接触算法、接触面行为等参数。3两摩擦片恒压加载工况下热应力仿真分析由理论分析可知[1]，实体模型的温差会导致相应的热应力，当实体部分节点位置处于约束状态时，容易造成应力分布的不均匀，局部热源的集中也会造成热应力过大[2]，致使摩擦盘产生热弹性形变，严重时会引起接触表面的凹凸不平，这种接触状态的改变反过来又影响了热源的输入，加剧了摩擦表面接触状态的复杂性。当加载时间较短、压力较低时，摩擦副表面的热应力并不显著，但是随着工作时间的增加，热应力随之增大，普通轻型汽车正常制动条件下摩擦表面的等效应力一般不会超过摩擦材料的强度极限[3]，然而用于负载模拟时，虽然推进油缸压力相对不高，但是加载时间一般却是普通制动时间的几十倍，摩擦副的接触状态既影响了盘式制动器的加载精度，同时也决定了合理的加载时间范围。图2表示加载结束时摩擦盘表面的热应力分布情况。图3表示摩擦盘表面不同半径处热应力随时间的变化情况（θ=0°)。图4表示摩擦盘不同厚度条件下热应力随时间的变化情况（θ=0°，r=0.25m）。图5表示摩擦盘表面不同周向夹角处的热应力随时间的变化情况（r=0.25m）。F计算值误差实际值(a)普通方法FU(b)Newton-Raphson法图1求解方法87654321801000-100-1800.080.150.20.258等效应力/Pa×106径向尺寸/m周向夹角/°图2加载结束时摩擦盘表面热应力分布等效应力/Pa×106864200.080.150.20.258010203040径向尺寸/m时间/s图3摩擦盘表面不同半径处热应力分布等效应力/Pa432101801000-100-180010203040时间/s周向夹角/°图4摩擦盘不同厚度热应力分布等效应力/Pa432100.0150.010.0050010203040时间/s径向尺寸/m王哲：盘式制动器热应力场仿真分析U×106×1069

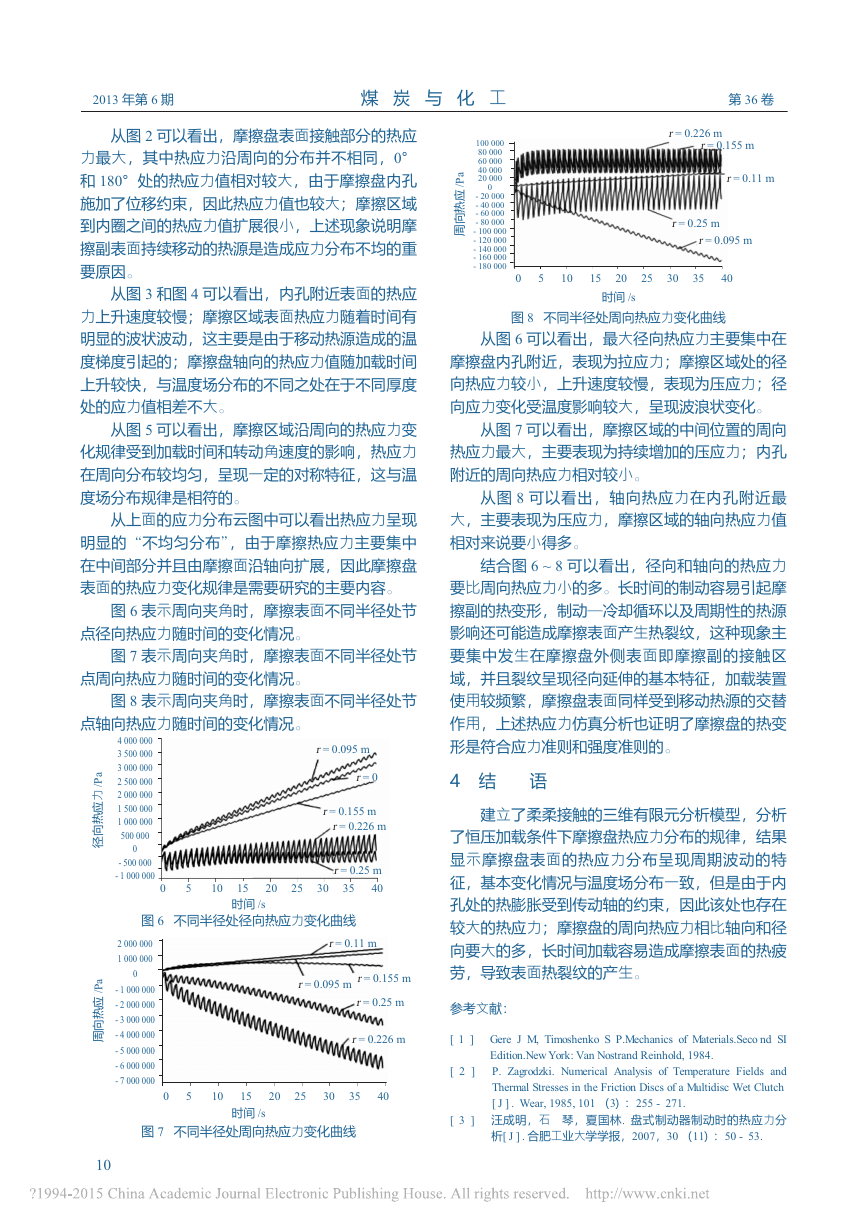
煤炭与化工2013年第6期第36卷从图2可以看出，摩擦盘表面接触部分的热应力最大，其中热应力沿周向的分布并不相同，0°和180°处的热应力值相对较大，由于摩擦盘内孔施加了位移约束，因此热应力值也较大；摩擦区域到内圈之间的热应力值扩展很小，上述现象说明摩擦副表面持续移动的热源是造成应力分布不均的重要原因。从图3和图4可以看出，内孔附近表面的热应力上升速度较慢；摩擦区域表面热应力随着时间有明显的波状波动，这主要是由于移动热源造成的温度梯度引起的；摩擦盘轴向的热应力值随加载时间上升较快，与温度场分布的不同之处在于不同厚度处的应力值相差不大。从图5可以看出，摩擦区域沿周向的热应力变化规律受到加载时间和转动角速度的影响，热应力在周向分布较均匀，呈现一定的对称特征，这与温度场分布规律是相符的。从上面的应力分布云图中可以看出热应力呈现明显的“不均匀分布”，由于摩擦热应力主要集中在中间部分并且由摩擦面沿轴向扩展，因此摩擦盘表面的热应力变化规律是需要研究的主要内容。图6表示周向夹角时，摩擦表面不同半径处节点径向热应力随时间的变化情况。图7表示周向夹角时，摩擦表面不同半径处节点周向热应力随时间的变化情况。图8表示周向夹角时，摩擦表面不同半径处节点轴向热应力随时间的变化情况。从图6可以看出，最大径向热应力主要集中在摩擦盘内孔附近，表现为拉应力；摩擦区域处的径向热应力较小，上升速度较慢，表现为压应力；径向应力变化受温度影响较大，呈现波浪状变化。从图7可以看出，摩擦区域的中间位置的周向热应力最大，主要表现为持续增加的压应力；内孔附近的周向热应力相对较小。从图8可以看出，轴向热应力在内孔附近最大，主要表现为压应力，摩擦区域的轴向热应力值相对来说要小得多。结合图6~8可以看出，径向和轴向的热应力要比周向热应力小的多。长时间的制动容易引起摩擦副的热变形，制动—冷却循环以及周期性的热源影响还可能造成摩擦表面产生热裂纹，这种现象主要集中发生在摩擦盘外侧表面即摩擦副的接触区域，并且裂纹呈现径向延伸的基本特征，加载装置使用较频繁，摩擦盘表面同样受到移动热源的交替作用，上述热应力仿真分析也证明了摩擦盘的热变形是符合应力准则和强度准则的。4结语建立了柔柔接触的三维有限元分析模型，分析了恒压加载条件下摩擦盘热应力分布的规律，结果显示摩擦盘表面的热应力分布呈现周期波动的特征，基本变化情况与温度场分布一致，但是由于内孔处的热膨胀受到传动轴的约束，因此该处也存在较大的热应力；摩擦盘的周向热应力相比轴向和径向要大的多，长时间加载容易造成摩擦表面的热疲劳，导致表面热裂纹的产生。参考文献：[1]GereJM,TimoshenkoSP.MechanicsofMaterials.SecondSIEdition.NewYork:VanNostrandReinhold,1984.[2]P.Zagrodzki.NumericalAnalysisofTemperatureFieldsandThermalStressesintheFrictionDiscsofaMultidiscWetClutch[J].Wear,1985,101（3）：255-271.[3]汪成明，石琴，夏国林.盘式制动器制动时的热应力分析[J].合肥工业大学学报，2007，30（11）：50-53.时间/s0510152025303540r=0.11mr=0.095mr=0.155mr=0.25mr=0.226m图8不同半径处周向热应力变化曲线时间/s图6不同半径处径向热应力变化曲线径向热应力/Pa图7不同半径处周向热应力变化曲线时间/s0510152025303540r=0.11mr=0.095mr=0.155mr=0.25mr=0.226m0510152025303540r=0.095mr=0.155mr=0.226mr=0.25m40000003500000300000025000002000000150000010000005000000-500000-1000000周向热应/Pa200000010000000-1000000-2000000-3000000-4000000-5000000-6000000-7000000r=0周向热应/Pa100000800006000040000200000-20000-40000-60000-80000-100000-120000-140000-160000-18000010