logo资料库

双像解析摄影测量.pdf

发布时间：2022-05-29 发布人：admin 分类：说明书 资料大小：0.73M 资料格式：pdf 举报 版权申诉
第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
资料共15页，剩余部分请下载后查看
    《摄影测量学》 课程设计报告书 1
    目录 一、作业任务 ............................................. 3 二、计算原理 ............................................. 4 2.1 点投影系数法计算原理 .............................. 4 2.2 共线方程严密法计算原理 ............................ 6 三、编程实现 ............................................. 7 四、计算结果 ............................................. 7 4.1 点投影系数法计算结果 .............................. 7 4.2 共线方程严密法计算结果 ............................ 8 五、学习体会 ............................................. 8 六、附录 ................................................. 9 6.1 点投影系数法源代码及运行截图 ...................... 9 6.2 共线方程严密法源代码及运行截图 ................... 11 2
    一、作业任务 已知一个立体像对： 左 像 片 的 外 方 位 元 素 为 : (14922.9778, 11532.4077, 3230.3383)m, (-0.0566, -0.1215, -0.6456)°， 右像片的外方位元素为: (16296.9601, 11524.2256, 3239.6070)m, (0.0429, -0.5148, -0.1538)°， 相机的内方位元素（x0, y0, f）为（-0.004，-0.008, 152.72）mm。 现量测了 6 个像点的框标坐标，如下（单位 mm）： 左片: 1(85.7255, 69.6561), 2(0.3206, 59.1841), 3(83.7954, -1.9617), 4(-2.2603, -15.1519), 5(88.2371,-73.7021), 6(2.4792,-67.5320) 右片: 1 ( 0.6313, 70.1653), 2 ( -84.4506, 60.4553), 3( -3.3174, -1.3205) 4 ( -97.0211, -13.7425), 5(2.7516, -72.5590), 6( -82.9161, -65.7818) 采用点投影系数法和共线方程严密法分别计算上述 6 个点的地面坐标。 3
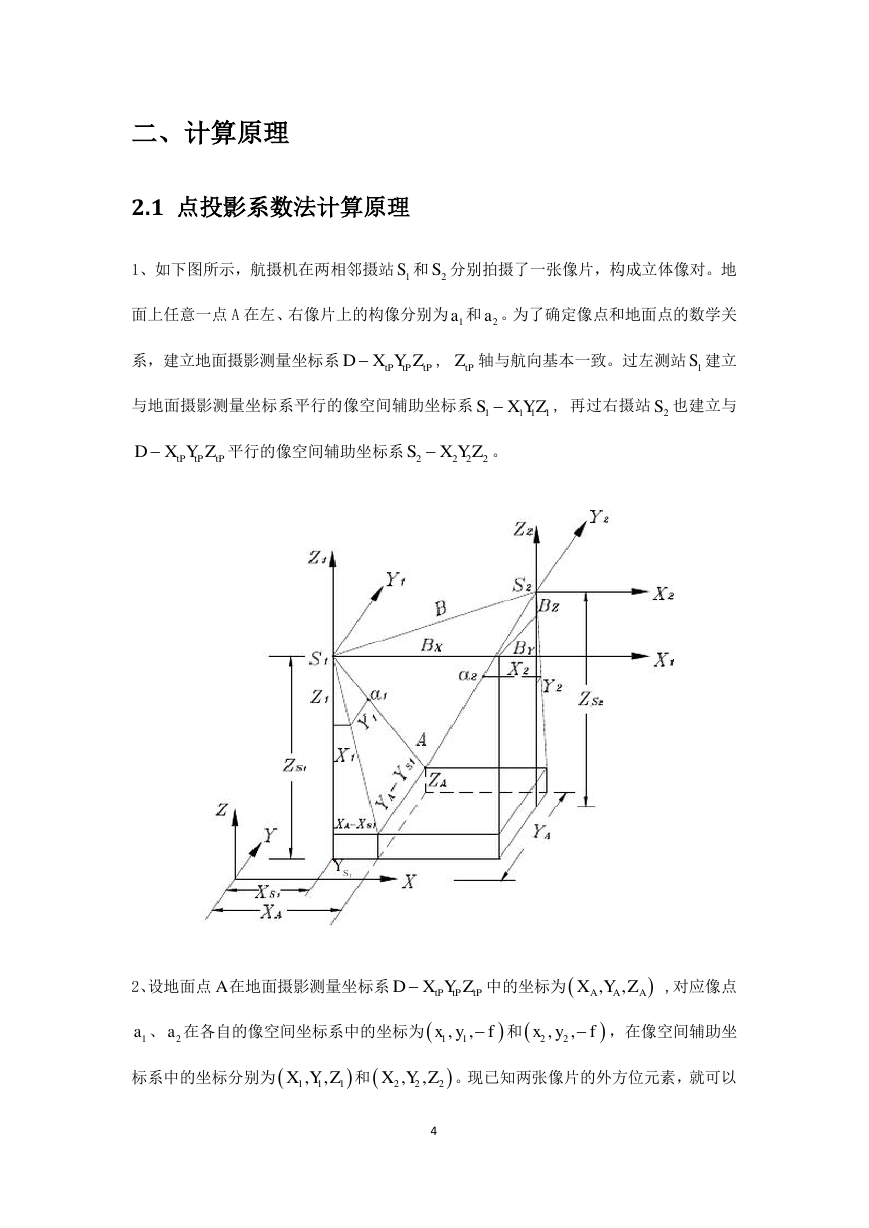
    二、计算原理 2.1 点投影系数法计算原理 1、如下图所示，航摄机在两相邻摄站 和 分别拍摄了一张像片，构成立体像对。地 面上任意一点 A 在左、右像片上的构像分别为 和 。为了确定像点和地面点的数学关 系，建立地面摄影测量坐标系 , 轴与航向基本一致。过左测站 建立 与地面摄影测量坐标系平行的像空间辅助坐标系 , 再过右摄站 也建立与 平行的像空间辅助坐标系 。 2、设地面点 在地面摄影测量坐标系 中的坐标为 ,对应像点 、 在各自的像空间坐标系中的坐标为 和 ，在像空间辅助坐 标系中的坐标分别为 和 。现已知两张像片的外方位元素，就可以 4 1S2S1a2atPtPtPDXYZtPZ1S1111SXYZ2StPtPtPDXYZ2222SXYZAtPtPtPDXYZ,,AAAXYZ1a2a11,,xyf22,,xyf111,,XYZ222,,XYZ
    由像点的像空间坐标计算出该点的像空间辅助坐标，即 上式中， 、 为由已知的外方位角元素算得的左、右像片的旋转矩阵。 3、右摄站 在 中的坐标，即摄影基线 的三个分量 、 、 可由外 方位直线元素算得 4、因为左、右像空间辅助坐标系与地面摄影测量坐标系相互平行，且摄站点、像点、 地面点、三点共线。则由上图可得 式中： 、 为左、右像点的投影系数。一般情况下，不同的点有不同的投影系数 值。 5、根据上式可以得到前方交会法计算地面点坐标的公式，即 式 中， 、 仍然未知，为此，结合式子 ，有 6、由式子 中的一、三两式联立求解投影系数得 5 112211121212,XxXxYRyYRyZfZf(211)1R2R2S1111SXYZBXBYBZB212121XSSYSSZSSBXXBYYBZZ(212)11122211111112222222ASASASASASASXXYYZZSANSaXYZXXYYZZSANSaXYZ(213)1N2N121212112211221122SSAASSASSXXXNXNXYYNYYNYZNZNZZZ(214)(214)1N2N(212)112211221122XYZBNXNXBNYNYBNZNZ(215)(215)
    2.2 共线方程严密法计算原理 1、一个地面点 分别对应左右两张像片两个点 、 ，每个像点对应两个共线方程， 即一个地面未知点对应四个共线方程 ，即 上式中， 、 、 分别表示旋转矩阵中的 中的 、 、 元素。 2、将四个共线方程分别对 X、Y、Z 进行线性化得到关于 X、Y、Z 三个未 知数的四个误差线性方程，即 上式中各系数和常数项分别为 6 22112211121221XZXZBZBXNXZXZBZBXNXZXZ(216)A1a2a111111111111222111111101313131212121013131321212120()()()()()()()()()()()()()()()ASASASASASASASASASASASASASASASaXXbYYcZZxxfaXXbYYcZZaXXbYYcZZyyfaXXbYYcZZaXXbYYcZZxxfa22222222223232322222220232323()()()()()()()()()ASASASASASASASASASXXbYYcZZaXXbYYcZZyyfaXXbYYcZZ(221)ijaijbijciRjajbjc11221112131415162122232425260000xyxylXlYlZllXlYlZllXlYlZllXlYlZl(222)
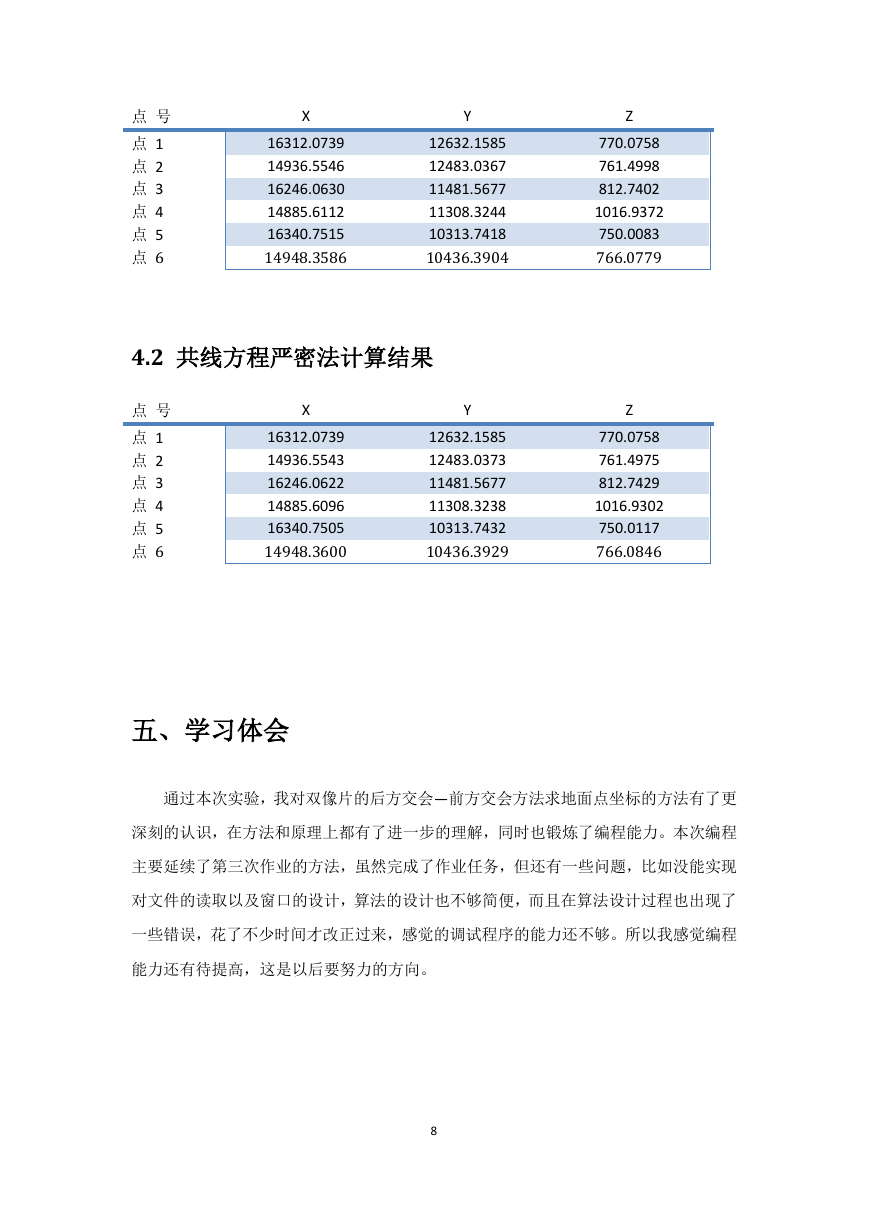
    其中， =1，2。 3、用矩阵形式表示误差方程式为： 其中 4、根据最小二乘原理，可以解的 三、编程实现 采用 C++语言进行了点投影系数法和共线方程严密法求地面点坐标的程序编写，源 代码和运行结果截图详见附录。 四、计算结果 4.1 点投影系数法计算结果 7 11032103310342035203620311103030322()()()()()()()()()iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiixiSiSiSiiSiiSiiSyiSilfaxxalfbxxblfcxxclfayyalfbyyblfcyyclfaXfbYfcZxxaXxxbYxxcZlfaXfbY2030303()()()iiiiiSiSiiSiiSiiSfcZyyaXyybYyycZiVAXL(223)1122111213141516212223242526,TxyxyllllllALllllllllll1()()TTXAAAL(224)
    X 16312.0739 14936.5546 16246.0630 14885.6112 16340.7515 14948.3586 Y 12632.1585 12483.0367 11481.5677 11308.3244 10313.7418 10436.3904 点 号 点 1 点 2 点 3 点 4 点 5 点 6 4.2 共线方程严密法计算结果 X 16312.0739 14936.5543 16246.0622 14885.6096 16340.7505 14948.3600 Y 12632.1585 12483.0373 11481.5677 11308.3238 10313.7432 10436.3929 点 号 点 1 点 2 点 3 点 4 点 5 点 6 Z 770.0758 761.4998 812.7402 1016.9372 750.0083 766.0779 Z 770.0758 761.4975 812.7429 1016.9302 750.0117 766.0846 五、学习体会 通过本次实验，我对双像片的后方交会—前方交会方法求地面点坐标的方法有了更 深刻的认识，在方法和原理上都有了进一步的理解，同时也锻炼了编程能力。本次编程 主要延续了第三次作业的方法，虽然完成了作业任务，但还有一些问题，比如没能实现 对文件的读取以及窗口的设计，算法的设计也不够简便，而且在算法设计过程也出现了 一些错误，花了不少时间才改正过来，感觉的调试程序的能力还不够。所以我感觉编程 能力还有待提高，这是以后要努力的方向。 8
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料