第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
论文研究-拉格朗日松弛的无人机路径规划.pdf
Computer Engineering and Applications 计算机工程与应用
2012，48（27）
233
拉格朗日松弛的无人机路径规划
刘 山 1，顾晔倩 1，李雨石 1，曹盛文 1，刘 轩 2
LIU Shan1, GU Yeqian1, LI Yushi1, CAO Shengwen1, LIU Xuan2
1.中国民航大学 计算机学院，天津 300300
2.麦基尔大学 电气和计算机工程系，魁北克 蒙特利尔 H3AoG4，加拿大
1.School of Computer Application, Civil Aviation University of China, Tianjin 300300, China
2.Department of Electrical and Computer Engineering, McGill University, Montréal, Quebec H3AoG4, Canada
LIU Shan, GU Yeqian, LI Yushi, et al. Lagrange relaxation for UAV path planning. Computer Engineering
and Applications, 2012, 48（27）：233-238.
Abstract：It proposes a path planning algorithm based on an urban building block model for Unmanned Air Vehicle
（UAV for short）.The proposed algorithm mainly contains two aspects. First the algorithm simulates the buildings in
urban environment with cylinders, so it’s able to calculate the block area of the relative position between the build-
ings and UAV. In addition, the total shading area isn’t the addition of each shading area, instead it’s a union set. The
algorithm calculates the union set by using a program. Second, after calculating the curved surface of UAV’s flight
plane, this algorithm proposes an optimal path planning method based on Lagrange relaxation of UAV. The path is a
polygonal line along the equant diagonal line on the searching area of UAV. The shading area of this path is mini-
mal. The Matlab simulation result suggests this algorithm is efficient.
Key words：Unmanned Air Vehicle（UAV）; path planning; urban environment; blocked; Lagrange relaxation algorithm
摘 要：提出了基于城市建筑物遮挡模型的无人驾驶飞行器（简称无人机）路径规划方法，主要包含两方面的
内容：一是利用圆柱体虚拟城市的建筑物环境，使建筑物对无人机的遮挡面积可计算，另外，由于建筑物的相
对位置会相互遮挡，不可以进行简单的面积加法。采用程序实现了无人机的遮挡总和的计算，即每个建筑物
遮挡面积的并集。二是在计算出无人机飞行的水平平面上（x，y）点的遮挡曲面值的基础上，给出了无人机基于
拉格朗日松弛算法的优化路径规划，即走一条遮挡面积最小的路径的方法。给出 matlab 仿真结果，实验结果表
明该方法是十分有效的。
关键词：无人机；路径规划；城市环境；遮挡；拉格朗日松弛算法
文章编号：1002-8331（2012）27-0233-06 文献标识码：A 中图分类号：TP391
1 引言
内的广泛关注和研究热潮[1-2]。
无人机在最近几十年得到了深入的研究和飞速
的发展，使得它的用途日益广泛。由于无人机成本
低，生存能力强，机动性好，使用性强等特性，使得其
在军用和民用领域都有广阔的应用前景，无人机及
其相关技术也获得了飞速的发展，引起了世界范围
路径规划的能力是无人机所必须具有的能力，
也是无人机自主飞行的重要技术研究领域之一。无
人机的路径规划是指在特的定约束条件下，依靠地
形信息和障碍信息，寻找从起始点到目标点并满足
无人机性能指标的最优或可行的路径。它是无人机
基金项目：国际合作与交流专项基金（No.2008DFA12300）。
作者简介：刘山（1955—），男，教授，研究领域：数据挖掘、计算机视频；顾晔倩（1985—），女，硕士研究生，研究领域：计算机视频；
李雨石（1987—），女，硕士研究生，研究领域：计算机视频；曹盛文（1987—），男，硕士研究生，研究领域：计算机视频；
刘轩（1982—），女，硕士研究生，研究领域：计算机视频。E-mail：yeqian0520@126.com
收稿日期：2011-03-18 修回日期：2011-06-02
DOI：10.3778/j.issn.1002-8331.2012.27.048
CNKI 出版日期：2011-08-04
http://www.cnki.net/kcms/detail/11.2127.TP.20110804.1607.087.html
234
2012，48（27）
Computer Engineering and Applications 计算机工程与应用
任务规划系统的关键技术，是确保无人机提高飞行
器效能，圆满完成侦查任务的有效手段。
目前，反恐防暴、消防救援的监测、侦查直接涉
及到国民经济建设和人民日常生活的安全，得到各
国政府的高度重视。无人机用于城市交通环境下进
行低空观察，既可与同步卫星和地面移动侦察机器
人配合，又可与定翼机大范围低空观测相互补充。
通过提高无人机自主飞行的性能，进行无人机路径
规划，可望大大增强和提升我国对城市、大工业区域
反恐防暴、消防救援、交通监控和安全保卫的能力。
近几年来，随着国民经济的发展，城市中机动车辆渐
渐增多，交通需求不断增加，由此导致了交通堵塞的
频繁发生，城市交通面临着越来越大的压力。因此，
对无人机进行路径规划，使其对路况信息做出准确
而及时的监控和反馈，从而有效避免堵塞和交通事
故的发生，有着广泛的研究意义。
无人机的路径规划主要是因为无人机所监控的
城市建筑和交通环境是十分复杂的，准确刻画无人
机在给定位置上观测到地面的面积是一个十分复杂
的问题。国外和国内的众多研究机构相继开展这方
面的研究工作。其中包括采用双向稀疏 A*算法[3]获
取对最优路径的搜索。Rosli Omar 等人分析了面向
能见度线的方法[4]，给出了克服大量障碍存在时无人
机的路径规划。另外有蚁群优化算法[5]，通过评价函
数值，来更新路径的信息素，搜索生成最初的航迹。
符小卫等将粒子群优化算法 [6]引入无人路径规划
中。而 J.Kim 与 Y.Kim 在 2009 年提出了城市环境下
基于环形路径的多无人机跟踪地面目标[7]。紧接着，
Kim 和 Jongrae Crassidis 分析了基于城市环境下地面
目标最大能见度的无人机路径规划[8]，文中将多个运
动目标，分为若干个小组，提出了一种循环路径的规
划方法，用于跟踪多个运动目标。
综上所述算法，存在搜索速度慢和耗内存空间
大的缺憾，而且都是通过实时搜索得到最优航迹，容
易陷入局部最优。本文在基于圆柱虚拟城市建筑物
环境的基础上，提出了一种基于拉格朗日松弛算法
的无人机路径规划方法。本方法是通过离线计算直
接获取的，具有计算精确可靠、效率高的优点。
2 城市环境遮挡模型
当无人机在城市上空执行飞行任务时，无人机
可能会被周围的建筑物等所遮挡，因此，要进行无人
机的路径规划，首先要解决无人机的遮挡问题。
在计算建筑物遮挡时，由于建筑物的相互遮挡
原因，遮挡的总面积是每个建筑物遮挡面积集合的
并集，需要用程序来实现。如图 1 所示，假设无人机
按飞行的高度为 H，无人机与建筑物顶部的仰角为α，
建筑物用一个圆柱体代替高度为 h，半径为 r，无人机
到建筑物中心水平距离为 a，投影圆的半径为 l。
Z
O
C″
H
h
B″
X
U 无人机
o
B′
B
α
r
F′
C′
α
Y
A
o′
c
o
A′
G
图 1 无人机被建筑物遮挡的面积示意图
在对城市的建筑物进行仿真时，采用圆柱体虚
拟城市建筑物（如图 2），使无人机在与建筑物任何相
对位置和方向上，都可以计算出该建筑物的遮挡面
积，即无人机被建筑物遮挡时看不到的地面面积。
Z
5
15
10
Y
5
10
X
15
20
图 2 城市建筑物的圆柱虚拟示意图
2.1 三角形 UBB′ 顶点坐标的计算
根据无人机被建筑物遮挡面积的俯视图，即图 3，
可以得到：UO 直线方程：过（Xu，Yu）和（Xr，Yr）点：
y = ax + (y
u
- y
- x
y
x
r
r
其中，a =
- ax
u
b = y
u
u
) = ax + b
- ax
u
u
。
（1）
B
（Xr，Yr）
A
（Xl，Yl）
O
U
（Xu，Yu）
B′
a
h′
A′
图 3 无人机被建筑物遮挡的面积俯视图
BB′ 直线方程：过（Xr，Yr）与 UO 直线垂直有：
刘 山，顾晔倩，李雨石，等：拉格朗日松弛的无人机路径规划
2012，48（27）
235
x + (y
+ 1
a
x
r
) = - 1
a
r
x + c
（2）
y = - 1
a
+ 1
a
r
其中c = y
。
x
r
B 和 B′ 点坐标：过（Xr，Yr）与 UO 直线距离为 r：
r = |ax - y + b|
ì
ïï
a2 + 1
í
ïï
x + c
î
y = - 1
a
解方程
X
ì
ï
ï
ïï
í
ï
ï
ïï
Y
î
BB′
= (c - b) ± r a2 + 1
a + 1
a
（3）
= (b - c) r a2 + 1
a2 + 1
+ c
BB′
同理可以计算出三角形 DUAA′ 的顶点坐标。
2.2 投影圆心坐标（Xl，Yl）和半径 L 的计算
根据图 4 所示，无人机被建筑物遮挡的面积侧视
图，通过无人机和建筑物的坐标，从而计算投影圆心
坐标和半径。计算过程如下：
tan α = H - h
α
\ α = H - h
tan α
同时 tan α = h
h'
\ h' = h
tan α
由等比关系可得：
=
r
l
a
a + h'
=
H - h
tan α
H - h
tan α
+ h
tan α
= H - h
tan α
Þ l = rH
H - h
投影圆心坐标（Xl，Yl）在 UO 直线上，距离 BB′ 直
线距离为 h′ ：
|
|| 1
a
x + y - c
|
||
ì
ï
h' =
ï
í
ï
ï
î
+ 1
1
a2
y = ax + b
ì
ï
ï
解方程：
í
ï
Y1 = (ac2 - b) ± h' a2 + 1
ï
î
X1 = a(c - b) ± h' a2 + 1
a2 + 1
a2 + 1
（4）
UAV
H
α
h
（Xu，Yu）
a
U
（Xr，Yr）
（Xl，Yl）
l
h′
图 4 无人机被建筑物遮挡的面积侧视图
2.3 判断点 P 在三角形 ABC 中的面积法
当存在多个建筑物时，无人机在（x，y）时遮挡面
积是有重叠的，为了不重复计算，首先要判断出地面
上每一个点是否被多次遮挡。
定义：平面上的三点 A(x1y1)B(x2y2)C(x3y3)
的面积量：
S(ABC) = 1
2
(y
1
)´(y
- y
) -
3
- x
´((x
1
2
)´(x
3
- y
2
2
))
3
- x
已知：三角形的三个顶点 A，B，C，及平面上的一
点 P。
算法描述如下：
算法 1 判断点 P 在 DABC 中的面积法
1
If abs（S（A，B，C））=abs（S（P，B，C））+abs（S（A，P，
C））+abs（S（A，B，P））
P 在三角形 ABC 的内部或边上；
2 then
3
4 End if
5
If abs（S（P，B，C））&&abs（S（A，P，C））&& abs（S（A，
B，P））>0
P 在三角形 ABC 内部；
Else
6 then
7
8
9
10 End if
11 if abs（S（A，B，C））
236
2012，48（27）
Computer Engineering and Applications 计算机工程与应用
then
B（x，y）=1；
End if
End
6
7
8
9
10
11
12 End
A（x，y）=sum（B（x，y）中 1 的个数）/L*L；
End
3 基于拉格朗日松弛算法的无人机路径规划
方法
拉格朗日松弛算法[9]可以用来处理带有时间约
束的最短路径问题，方法是可以改变任何在通过时
间上的非负通行费，找到在约束的最短路径的长度
上的下界。受约束的最短路径[10]的描述如下。
给出：网络 G = (NA),c
为弧 (ij) 的代价，t
为
ij
ij
对弧 (ij) 的遍历时间。
Z* = Min å
c
ij
x
ij
(ij)Î A
水平飞行的平面平均分割成正方形的格子 A(Ij) ，各
自的交点上具有遮挡数值，如图 5 所示。
1
2
3
4
5
1
2
3
4
5
图 5 离散化建筑物的遮挡曲面示意图
每 个 栅 格 A(nn) 上 的 邻 接 关 系 与 时 间 代 价
mtime(n ´ nn ´ n) 和花费代价 mcost(n ´ nn ´ n) 的邻
接矩阵的转换（按行存储栅格点），如图 6。
（i，j）
（i，j+1）
（5）
1
1.414
1
1
（i+1，j）
（i+1，j）
（i+1，j+1）
（i，j）
A（i，j+1） （i，j+1）
A（i+1，j）
A（i+1，j+1）
A（i+1，j+1）
A（i+1，j+1）
（i+1，j）
（i+1，j+1）
图 6 矩阵间的转换示意图
4 算法验证与仿真
无人机路径规划的拉格朗日松弛算法的实现，
输入遮挡栅格矩阵，生成代价矩阵和时间矩阵，最后
输出遮挡栅格矩阵的路径规划结果，并以粒子群优
化（PSO）算法为例，进行了比较。由结果可以看出，
通过该算法，无论飞行区域的大小，无人机均能在限
制时间内，找到遮挡面积最小的路径。
为了能够清楚地证明本文给出算法的有效性，
首先以小范围飞行为例，在 n = 3，即将无人机的飞行
区域划分为 3×3 的矩阵，时间约束为 10 的情况下，如
图 7 所示为代价和时间矩阵。
经过计算，得到的结果为：
Path=1
2 5
Time=5.696 4
9
s.t. å
j
x
ij
- å
x
=
ji
i = s
i = t
1,
ì
ï
-1,
í
ï
0, otherwise
î
t
j
£ T 复杂的约束
å
= 0 or 1 for all(ij)Î A
(ij)Î A
x
x
ij
ij
ij
3.1 基于拉格朗日松弛模型的转换过程
将“松弛”复杂约束，然后使用惩罚太多通过时
间的“启发式方法”，然后把它和拉格朗日松弛理论
联系在一起。根据式（1），做如下改变：
对于每个 μ ³ 0，通过下式替换目标：
Z(μ) = Min å
+ μ( å
x
x
c
t
- T) =
ij
ij
ij
ij
(ij)Î A
å
(ij)Î A
(c
+ μt
ij
(ij)Î A
）x
ij
ij
- μT
那么，对于 μ ³ 0，有 Z(μ) £ Z* 因为：
å
x
t
ij
ij
£ T
(ij)Î A
可以改变任何在 μ 通过时间上的非负通行费。
对路径 P 令：
= å
c
c
P
= å
, t
ij
P
(ij)Î P
(ij)Î P
对固定的 μ 和 P ，令 c
t
ij
(μ) = å
(ij)Î P
P
[c
ij
+ μt
] 。
ij
界限原则：假设 μ ³ 0 ，P 是关于修改代价 c
(μ)
(μ) - μT 是在约束的最短经
P
的最小代价路径，那么 c
的长度上的下界。
3.2 拉格朗日松弛模型的数据准备
P
离散化建筑物的遮挡曲面为栅格，即将无人机
刘 山，顾晔倩，李雨石，等：拉格朗日松弛的无人机路径规划
2012，48（27）
237
1
（0.2，4.1）
2
（0.5，5.0）
3
（0.2，1.3）
（0.4，2.6）
（0.4，0.4）
（0.1，4.8）
5
（0.0，3.9）
（0.5，0.7）
（0.4，0.2）
）
7
.
，0
1
.
0
（
）
1
.
6
，3
9
.
0
（
（0.2，1.2）
（0.1，2.0）
8
（0.3，4.0） 9
）
6
.
，4
4
.
0
（
4
）
9
.
，2
9
.
0
（
7
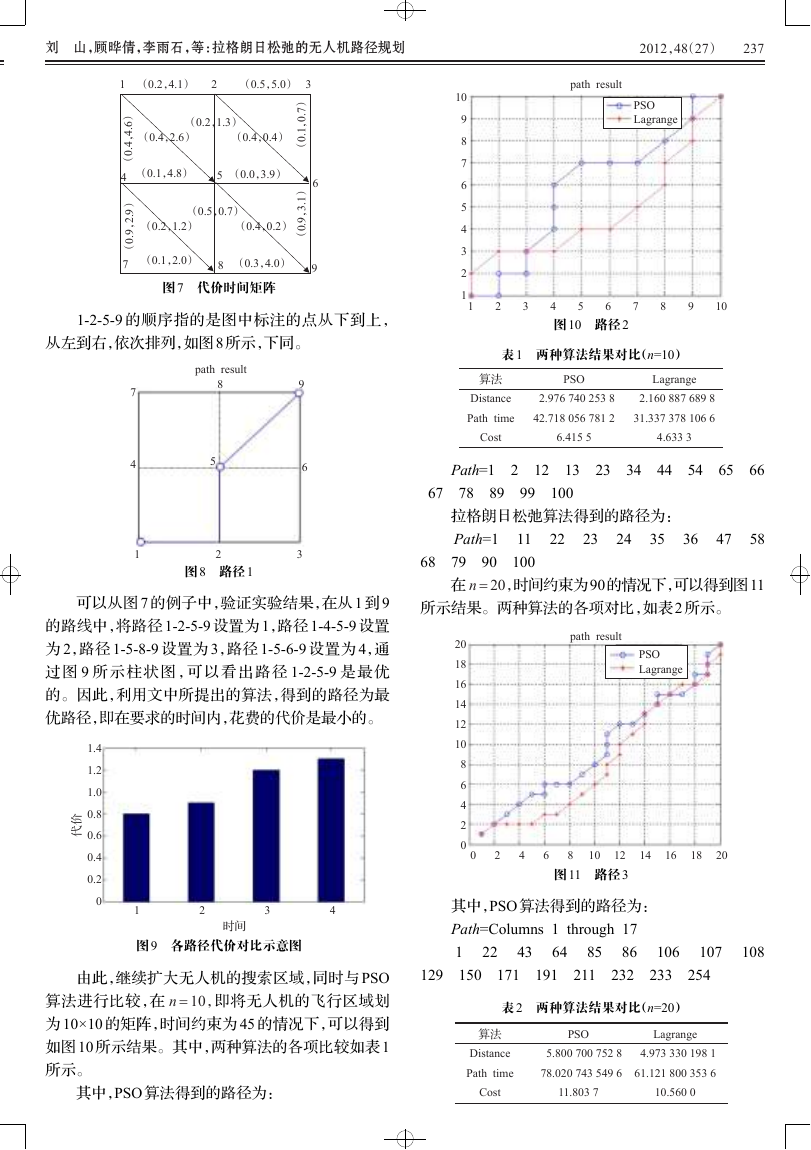
图 7 代价时间矩阵
1-2-5-9 的顺序指的是图中标注的点从下到上，
从左到右，依次排列，如图 8 所示，下同。
7
4
path result
8
5
9
6
1
2
3
图 8 路径 1
可以从图 7 的例子中，验证实验结果，在从 1 到 9
的路线中，将路径 1-2-5-9 设置为 1，路径 1-4-5-9 设置
为 2，路径 1-5-8-9 设置为 3，路径 1-5-6-9 设置为 4，通
过图 9 所示柱状图，可以看出路径 1-2-5-9 是最优
的。因此，利用文中所提出的算法，得到的路径为最
优路径，即在要求的时间内，花费的代价是最小的。
1.4
1.2
1.0
0.8
0.6
0.4
0.2
0
价
代
1
2
3
4
时间
图 9 各路径代价对比示意图
由此，继续扩大无人机的搜索区域，同时与 PSO
算法进行比较，在 n = 10，即将无人机的飞行区域划
为 10×10 的矩阵，时间约束为 45 的情况下，可以得到
如图 10 所示结果。其中，两种算法的各项比较如表 1
所示。
其中，PSO 算法得到的路径为：
10
9
8
7
6
5
4
3
2
1
1
2
3
path result
PSO
Lagrange
6
5
4
图 10 路径 2
7
8
9
10
表 1 两种算法结果对比（n=10）
算法
PSO
Lagrange
Distance
Path time
2.976 740 253 8
42.718 056 781 2
2.160 887 689 8
31.337 378 106 6
Cost
6.415 5
4.633 3
Path=1
2
12
13
89 99 100
67 78
23
34
44
54
65
66
拉格朗日松弛算法得到的路径为：
Path=1
22
23
24
35
11
90 100
68 79
36
47
58
在 n = 20，时间约束为90的情况下，可以得到图11
所示结果。两种算法的各项对比，如表 2 所示。
20
18
16
14
12
10
8
6
4
2
0
0
2
4
6
path result
PSO
Lagrange
8
10
12
图 11 路径 3
14
16
18
20
其中，PSO 算法得到的路径为：
Path=Columns 1 through 17
1
86
191 211 232
22
43
64
85
129 150 171
107
106
233 254
108
表 2 两种算法结果对比（n=20）
算法
Distance
Path time
Cost
PSO
Lagrange
5.800 700 752 8
78.020 743 549 6
4.973 330 198 1
61.121 800 353 6
11.803 7
10.560 0
238
2012，48（27）
Computer Engineering and Applications 计算机工程与应用
Columns 18 through 27
275
297
379 400
295
296
318
338
339
359
拉格朗日松弛算法得到的路径为：
Path=Columns 1 through 17
1
22
46
24
25
192 213 234 254
23
131 151 172
47
68
89
110
Columns 18 through 26
318
275
296
317
339
359
360
380
400
通过以上实验结果，可以得出，在同样的飞行环
境下，文中所提出的算法，无论在距离、时间和代价
上，都明显优于粒子群优化算法。生成的路径，不仅
满足时间要求，而且保证了遮挡面积的最小，从而验
证了算法的有效性。
5 结论
无人机应用领域从单纯的军事领域逐渐扩展至
民用领域，其普及程度大大提高。本文通过两个主
要的模型：圆柱虚拟城市环境模型和基于时间约束
的水平飞行平面遮挡面积最小化模型，给出了无人
机最优路径的规划方法，该方法与以往此问题的启
发式解决方法的不同点：一是计算精确可靠、效率
高。二是研究成果到实用没有跨度，利用此方法可
直接开发出任意城市的无人机路径规划系统。必
将会对未来的城市安防和城市交通监控起到重大
的作用。
参考文献：
[1] Kevin B J.Splined based path planning for Unmanned
Air Vehicles[C]//Proceedings of the AIAA Guidance，Navi-
gation and Control Conference，2001：254-257.
[2] Timothy W，Randal W B.Trajectory planning for coordi-
nated Rendezvous for unmanned air vehicles[R].AIAA
2000-4370-CP，2000.
[3] Meng Bobo，Gao Xiaoguang.UAV path planning based on
bidirectional sparse A* search algorithm[C]//Intelligent
Computation Technology and Automation（ICICTA），2010.
[4] Omar R，Gu Dawei.Visibility line based methods for
UAV path planning[C]//ICROS-SICE，2009.
[5] Zhang Chao，Zhen Ziyang，Wang Daobo，et al.UAV path
planning method based on ant colony optimization[C]//
Control and Decision Conference（CCDC），2010.
[6] Bao Yong，Fu Xiaowei，Gao Xiaoguang.Path planning for
reconnaissance UAV based on Particle Swarm Optimiza-
tion[C]//The Second International Conference on Computa-
tional Intelligence and Natural Computing Proceedings
（CINC），2010.
[7] Kim J，Kim Y.Optimal circular flight of multiple UAVs
for target tracking in urban areas[R].2009：345-358.
[8] Kim，Crassidis J，John L.UAV path planning for maxi-
mum visibility of ground targets in an urban area[C]//
Proceedings of the 13th Conf on Information Fusion，
2010.
[9] 周莉，隋蕾，沙秀艳.利用拉格朗日松弛算法求解三维分配
问题[J].烟台师范学院学报，2006，22（2）：102-104.
[10] 胡耀民，刘伟铭.多约束最短路径模型与求解[J].湖南科技
大学学报，2010（1）.
（上接 232 页）
[7] 潘文霞.双层土壤参数的优化计算[J].中国电机工程学报，
1996，16（5）：358-360.
[12] 何智强，蒋正龙，周卫华，等.利用遗传算法对土壤模型的
反演计算[J].高电压技术，2007，33（9）：90-94.
[13] 付龙海，吴广宁，王颢，等.青藏铁路望楚段变电站土壤结
[8] 杨慧娜，谢桦，李中新.接地设计中两层土壤参数的优化计
构参数的确定[J].高电压技术，2006，32（2）：84-86.
算[J].现代电力，1999，16（1）：58-65.
[9] 周秧，李勐，索春梅，等.分层土壤中接地网参数的数值计
算[J].东北电力大学学报，2006，26（4）：32-35.
[10] Nahman J，Salamon D.A practical method for the inter-
pretation of earth resistivity data obtained from driven
rod tests[J].IEEE Trans on Power Delivery，1988，3（4）：
1375-1379.
[11] Dawalibi F，Blattner C J.Earth resistivity measurement
interpretation techniques[J].IEEE Trans on Power Appa-
ratus and Systems，1984，103（2）：374-382.
[14] 赵志斌，索志刚.复杂测试条件下分层土壤模型的建立[J].
高电压技术，2011，37（5）：1281-1287.
[15] 唐天兵，申文杰，韦凌云，等.一种改进的多目标混合遗
传 算 法 及 应 用 [J]. 计 算 机 工 程 与 应 用 ，2010，46（22）：
242-244.
[16] 薛毅.最优化原理与方法[M].北京：北京工业大学出版社，
2001.
[17] 江建.精英自适应混合遗传算法及其实现[J].计算机工程
与应用，2009，45（27）：34-35.
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
