第1页 / 共15页
第2页 / 共15页
第3页 / 共15页
第4页 / 共15页
第5页 / 共15页
第6页 / 共15页
第7页 / 共15页
第8页 / 共15页
pybrain 教程.docx
构建网络
1、 前馈网络
——如何建立一个多层感知器？
首先，构建一个前馈网络对象：
>>> from pybrain.structure import FeedForwardNetwork
>>> n = FeedForwardNetwork()
然后，构建输入层、隐层、输出层：
>>> from pybrain.structure import LinearLayer, SigmoidLayer
>>> inLayer = LinearLayer(2)
>>> hiddenLayer = SigmoidLayer(3)
>>> outLayer = LinearLayer(1)
把它们加入到网络中：
>>> n.addInputModule(inLayer)
>>> n.addModule(hiddenLayer)
>>> n.addOutputModule(outLayer)
我们可以添加多个输入和输出模块。网络必须知道它的哪个模块是输入模块和输出模块，以
便前向传播输入、反向传播误差。
然后，构建每层之间的连接（例如全连接）：
>>> from pybrain.structure import FullConnection
>>> in_to_hidden = FullConnection(inLayer, hiddenLayer)
>>> hidden_to_out = FullConnection(hiddenLayer, outLayer)
把它们加入到网络中：
>>> n.addConnection(in_to_hidden)
>>> n.addConnection(hidden_to_out)
现在，所有的元素已经到位，我们使用.sortModules()方法使得 MLP 可用：
>>> n.sortModules()
2、 激活神经网络
>>> n.activate([1,2])
array([-0.11302355])
输出可能是不同的，因为网络是被随机初始化的。想要查看参数，只需要查看.params 域：
>>> in_to_hidden.params
array([ 1.37751406,
-1.27774679])
>>> hidden_to_out.params
1.39320901, -0.24052686, -0.67970042, -0.5999425 ,
array([-0.32156782, 1.09338421,
0.48784924])
或：
>>> n.params
array([ 1.37751406,
1.39320901, -0.24052686, -0.67970042, -0.5999425 ,
-1.27774679, -0.32156782,
1.09338421,
0.48784924])
3、 检查网络结构
>>> print n
FeedForwardNetwork-6
Modules:
[, ,
]
Connections:
[
'SigmoidLayer-7'>,
'LinearLayer-8'>]
4、 为网络结构命名
即给网络一个 id。即这个网络有一个属性.name。如果没有给网络命名，则会自动产生一个
名字。
网络的构件也是：
>>> LinearLayer(2)
>>> LinearLayer(2, name="foo")
5、 递归神经网络 Recurrent Networks
与 FeedForward Networks 不同，Recurrent Networks 可以保存历史，某些学习算法需要它，
缺点是消耗内存。
构建一个递归神经网络：
>>> from pybrain.structure import RecurrentNetwork
>>> n = RecurrentNetwork()
>>> n.addInputModule(LinearLayer(2, name='in'))
>>> n.addModule(SigmoidLayer(3, name='hidden'))
>>> n.addOutputModule(LinearLayer(1, name='out'))
>>> n.addConnection(FullConnection(n['in'], n['hidden'], name='c1'))
>>> n.addConnection(FullConnection(n['hidden'], n['out'], name='c2'))
递归神经网络有一种额外的方法：.addRecurrentConnection()：
>>> n.addRecurrentConnection(FullConnection(n['hidden'], n['hidden'],
name='c3'))
如果我们现在激活网络，会得到这样的输出：
>>> n.sortModules()
>>> n.activate((2, 2))
array([-0.1959887])
>>> n.activate((2, 2))
array([-0.19623716])
>>> n.activate((2, 2))
array([-0.19675801])
我们也可以清楚网络的历史记录，即 reset()方法：
>>> n.reset()
>>> n.activate((2, 2))
array([-0.1959887])
>>> n.activate((2, 2))
array([-0.19623716])
>>> n.activate((2, 2))
array([-0.19675801])
构造一个用于分类的数据集，训练网络，展示结果。
使用前馈神经网络来分类
首先导入必要构件：
from pybrain.datasets
from pybrain.utilities
from pybrain.tools.shortcuts
from pybrain.supervised.trainers import BackpropTrainer
from pybrain.structure.modules
import ClassificationDataSet
import percentError
import buildNetwork
import SoftmaxLayer
pylab 是用来图形化输出的：
from pylab import ion, ioff, figure, draw, contourf, clf, show, hold, plot
from scipy import diag, arange, meshgrid, where
from numpy.random import multivariate_normal
我们用一个 2D 的数据集，分为 3 类。从文件中读取这个数据集（如 pylab.load()）：
means = [(-1,0),(2,4),(3,1)]
cov = [diag([1,1]), diag([0.5,1.2]), diag([1.5,0.7])]
alldata = ClassificationDataSet(2, 1, nb_classes=3)
for n in xrange(400):
for klass in range(3):
input = multivariate_normal(means[klass],cov[klass])
alldata.addSample(input, [klass])
随机设为 75%的训练集和 25%的测试集：
tstdata, trndata = alldata.splitWithProportion( 0.25 )
每个类别一个输出神经元。
trndata._convertToOneOfMany( )
tstdata._convertToOneOfMany( )
输出数据集信息：
print "Number of training patterns: ", len(trndata)
print "Input and output dimensions: ", trndata.indim, trndata.outdim
print "First sample (input, target, class):"
print trndata['input'][0], trndata['target'][0], trndata['class'][0]
现在，建立一个 5 个隐层单元的前馈网络，使用 buildNetwork()函数。输入层、输出层与输
入数据维度、类别维度一致。可以添加隐藏层。
输出层使用 softmax()函数。
fnn=buildNetwork(trndata.indim,5,trndata.outdim,outclass=SoftmaxLayer)
建立一个训练器，把网络和训练数据集作为它的输入。我们这里使用 BackpropTrainer：
trainer = BackpropTrainer( fnn, dataset=trndata, momentum=0.1, verbose=True,
weightdecay=0.01)
我们得到一个漂亮的轮廓，用一个方格网的数据点，放到数据集中。因此数据集的目标值可
以被忽略。
ticks = arange(-3.,6.,0.2)
X, Y = meshgrid(ticks, ticks)
griddata = ClassificationDataSet(2,1, nb_classes=3)
for i in xrange(X.size):
# 需要列向量，而不是数组
griddata.addSample([X.ravel()[i],Y.ravel()[i]], [0])
griddata._convertToOneOfMany()
开始训练迭代：
for i in range(20):
trainer.trainEpochs（1）
trnresult = percentError( trainer.testOnClassData(),
trndata['class'] )
tstresult = percentError( trainer.testOnClassData(
dataset=tstdata ), tstdata['class'] )
print "epoch: %4d" % trainer.totalepochs, \
"
"
train error: %5.2f%%" % trnresult, \
test error: %5.2f%%" % tstresult
out = fnn.activateOnDataset(griddata)
out = out.argmax(axis=1)
out = out.reshape(X.shape)
# 最大激活值作为类别
figure(1)
# interactive graphics off
ioff()
# clear the plot
clf()
hold(True) # overplot on
for c in [0,1,2]:
here, _ = where(tstdata['class']==c)
plot(tstdata['input'][here,0],tstdata['input'][here,1],'o')
if out.max()!=out.min():
# safety check against flat field
contourf(X, Y, out)
# interactive graphics on
# update the plot
# plot the contour
ion()
draw()
ioff()
show()
一个数据集可以被看做一组已命名的二维数组，称为“域”。DS 可以实现 DataSet：
使用数据集
inp = DS['input']
第一个输入向量：
inp[0,:]
还有期望输输出，遵循相同的规则。
如何遍历数据集：
for inp, targ in DS:
...
也可以一个一个地向数据集中增加数据：
for inp, targ in samples:
DS.appendLinked(inp, targ)
或者：
assert(ia.shape[0] == ta.shape[0])
DS.setField('input', ia)
DS.setField('target', ta)
用后一种方法不能查看联接数组维度，否则它就不可能从头开始构建一个数据集。
你也可以添加你自己的联接或非联接数据，但是训练的迭代可能会崩溃：
DS.addField('myfield')
DS.setField('myfield', myarray)
DS.linkFields('input','target','myfield') # must provide complete list here
随机产生训练集和测试集：
>>> len(DS)
100
>>> TrainDS, TestDS = DS.splitWithProportion(0.8)
>>> len(TrainDS), len(TestDS)
(80, 20)
1、 有监督数据集（for 监督回归训练）
包含两个域：输入和目标输出。大小必须在创建时设定。
>>> from pybrain.datasets import SupervisedDataSet
>>> DS = SupervisedDataSet( 3, 2 )
>>> DS.appendLinked( [1,2,3], [4,5] )
>>> len(DS)
1
>>> DS['input']
array([[ 1.,
2.,
3.]])
2、 顺序数据集（for 监督顺序回归训练）
新概念：sequences。
本质上讲，它的维度被分成可变长度的序列：
getNumSequences()
getSequence(index)
getSequenceLength(index)
创建一个顺序数据集也包含输入和输出域。顺序数据集 继承了有监督数据集，有监督数据
集也可以看成是 每个序列长度都为 1 的顺序数据集。
怎么向数据集中添加数据：
在每个序列被存储的时候，先调用 newSequence()，然后像上面一样 appendLinked()。
遍历顺序数据集：
for i in range(DS.getNumSequences):
for input, target in DS.getSequenceIterator(i):
# do stuff
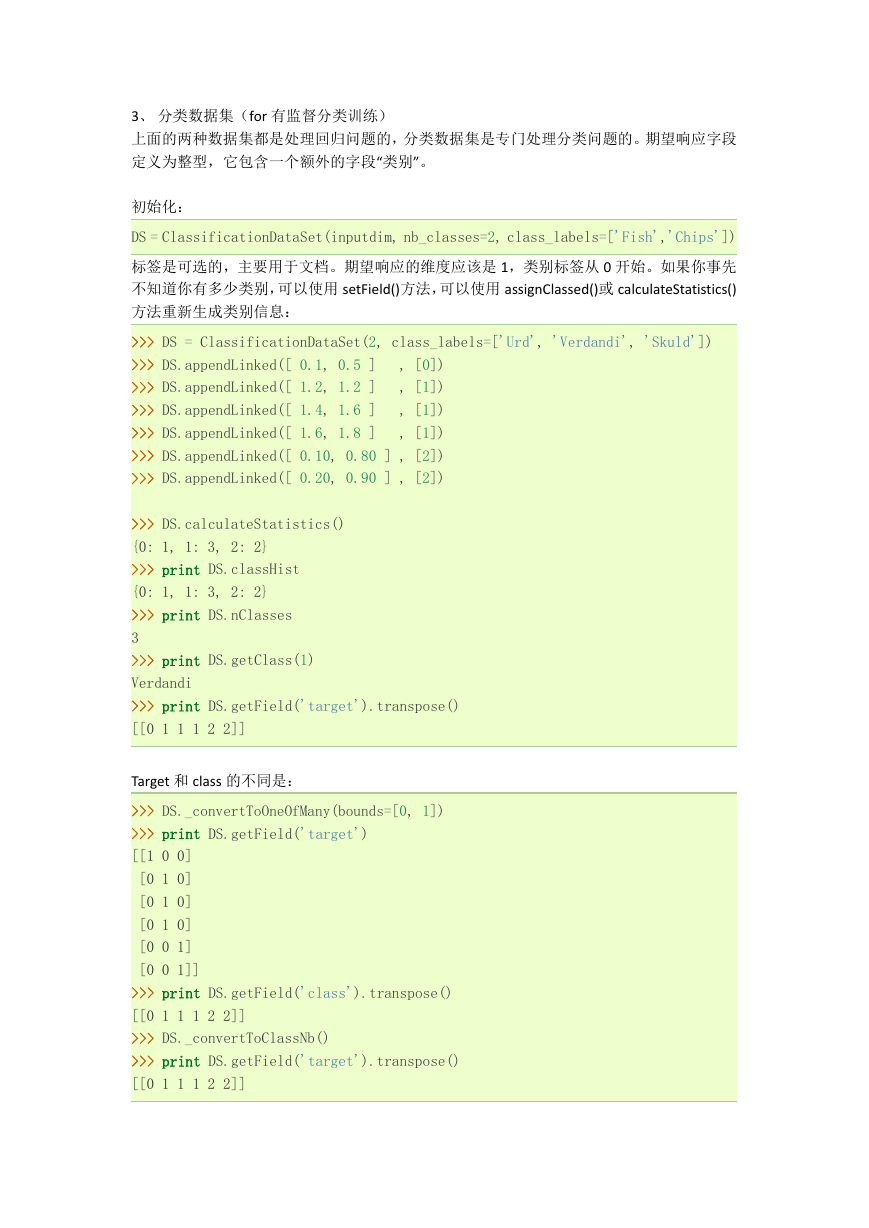
3、 分类数据集（for 有监督分类训练）
上面的两种数据集都是处理回归问题的，分类数据集是专门处理分类问题的。期望响应字段
定义为整型，它包含一个额外的字段“类别”。
初始化：
DS = ClassificationDataSet(inputdim, nb_classes=2, class_labels=['Fish','Chips'])
标签是可选的，主要用于文档。期望响应的维度应该是 1，类别标签从 0 开始。如果你事先
不知道你有多少类别，可以使用 setField()方法，可以使用 assignClassed()或 calculateStatistics()
方法重新生成类别信息：
>>> DS = ClassificationDataSet(2, class_labels=['Urd', 'Verdandi', 'Skuld'])
, [0])
>>> DS.appendLinked([ 0.1, 0.5 ]
, [1])
>>> DS.appendLinked([ 1.2, 1.2 ]
, [1])
>>> DS.appendLinked([ 1.4, 1.6 ]
>>> DS.appendLinked([ 1.6, 1.8 ]
, [1])
>>> DS.appendLinked([ 0.10, 0.80 ] , [2])
>>> DS.appendLinked([ 0.20, 0.90 ] , [2])
>>> DS.calculateStatistics()
{0: 1, 1: 3, 2: 2}
>>> print DS.classHist
{0: 1, 1: 3, 2: 2}
>>> print DS.nClasses
3
>>> print DS.getClass(1)
Verdandi
>>> print DS.getField('target').transpose()
[[0 1 1 1 2 2]]
Target 和 class 的不同是：
>>> DS._convertToOneOfMany(bounds=[0, 1])
>>> print DS.getField('target')
[[1 0 0]
[0 1 0]
[0 1 0]
[0 1 0]
[0 0 1]
[0 0 1]]
>>> print DS.getField('class').transpose()
[[0 1 1 1 2 2]]
>>> DS._convertToClassNb()
>>> print DS.getField('target').transpose()
[[0 1 1 1 2 2]]
4、 重要性数据集（for 权重有监督训练）
顺序数据集允许为每个部分分配不同的权重，0.0~1.0 之间。特例是每个权重都是 1.0。
黑盒子优化
介绍 pybrain 中的优化算法。
很多实际问题都可以被看做是一个优化问题：寻找控制器的最佳设置、最小化投资风险、寻
找一个游戏的最佳策略等等。常常包括决定一系列的变量，最大化或最小化目标函数。
优化问题的主要策略是从以下几个方面中选择变量：
所有实数：连续优化。
有范围的实数：约束优化。
整数：整数规划。
上面的组合。
其他。例如：图。
这些可以根据目标函数的特性进一步分类，例如：连续、偏导明确可达、二次型等等。
在黑盒子优化中，目标函数就是一个黑盒子，例如：没有条件。
Pybrain 的优化工具提供了最一般、都是黑盒子的情况。分为 2 类：
BlackBoxOptimizer，适用于所有类型的变量集。
ContinuousOptimizer，只能用于连续的优化。
1、 连续优化
首先定义一个简单的目标函数，连续的变量，例如：平方和：
>>> def objF(x): return sum(x**2)
和一个初始猜测从哪里开始看：
>>> x0 = array([2.1, -1])
现在，我们可以初始化一种优化算法，例如：CMAES：
>>> from pybrain.optimization import CMAES
>>> l = CMAES(objF, x0)
默认情况下，所有的优化算法都是最大化目标函数，但是你也可以通过设置 minimize 属性
来改成最小化目标函数：
>>> l.minimize = True
或者在构造的时候 直接写成：
CMAES(objF, x0, minimize = True)
优化结束的标准可以由算法决定，也可以通过：
评估的最大值
学习步骤的最大值
达到一个期望值
如：
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
