220 2017，53（2） Computer Engineering and Applications 计算机工程与应用 引入高阶 P-Laplace 的图像全变分盲复原方法 吴亚娟，徐黎明 WU Yajuan, XU Liming 西华师范大学 计算机学院，四川 南充 637009 College of Computer Science, China West Normal University, Nanchong, Sichuan 637009, China WU Yajuan, XU Liming. Total variation blind restoration using high-order P-Laplace. Computer Engineering and Applications, 2017, 53（2）：220-224. Abstract：To solve the problems of deterministic blind restoration, like the special phenomena of ringing and insufficient suppression noise, the high-order P-Laplace operator is introduced into the classical total variation restoration methods. Firstly, shock filter is used to predict the clear edges of images, and then deal with edge and internal smooth region of images in different forms respectively according to changing rules of the natural image pixels. Finally, it restores the images by split Bregman iteration and alternating minimization algorithm. The experimental results show that the improved algorithm proposed in the paper can alleviate the ringing phenomenon, protect edge information and ameliorate the effects of image restoration compared to a number of blind restoration algorithms in recent years. Key words：deterministic blind restoration; high-order P-Laplace; total variation; split Bregman; alternating minimization 摘 要：针对确定性盲复原中的振铃、阶梯现象和噪声抑制不充分的问题，将高阶 P-Laplace 算子引入到经典的全变分 盲复原方法中。首先利用 shock 滤波器进行清晰边缘预测，后根据自然图像中像素的变化规律，对图像的边缘和平滑 区域进行不同形式的处理，最后采用分裂布雷格曼迭代和交替最小化算法对非约束扩散方程进行求解。实验结果证 明，与近年的一些盲复原算法相比，提出的改进算法能较好地缓解振铃现象，保护好边缘信息并改善图像复原效果。 关键词：确定性盲复原；高阶 P-Laplace；全变分；分裂布雷格曼；交替最小化 文献标志码：A 中图分类号：TP391.41 doi：10.3778/j.issn.1002-8331.1607-0125 1 引言 在图像获取、传输、压缩、解压、存储等过程中都易 引起图像缺失或退化[1]。例如：由于物体、设备的运动， 场景不稳定等引起的模糊；在图像传输过程中加入噪 声，受到高斯白色噪声的影响。此外大气湍流扩散也会 引起模糊。退化图像通常可以简化为线性移不变卷积 核与高斯白噪声之和。在二维线性移不变系统[2]中，退 化图像的模型定义为： g(xy) = h(xy) ⊗ f (xy) + n(xy) 其中，g(xy) 为退化图像，f (xy) 是理想图像，h(xy) 为点扩散函数（Point Spread Function，PSF），n(xy) 为 白色加性噪声，⊗ 为卷积操作。 将退化图像恢复成原始的清晰图像即图像复原，根 据PSF是否已知将图像复原分为图像非盲复原（Non-Blind Image Restoration）和图像盲复原（Blind Image Resto- ration）。图像盲复原是在 PSF 未知或已知信息较少的 情况下根据模糊图像的相关数据进行恢复[3]。相关算法 按照图像模型可以分为随机性方法和确定性方法。前 者基于统计方法对图像和噪声进行建模，并利用相关的 统计信息作为正则化约束项进行求解，旨在寻找具有给 定方差的图像或者属于特定分布的图像。此类算法较 多，如文献[4-8]提到的算法。 确定性方法则通过最小化残差范数估计原始图 像。以 Chan 等人提出的基于全变分范数的盲复原方法[9] （Total Variation，TV）为代表，通过添加正则化约束项将 求解盲反卷积中的病态问题转变成良态问题。Babacan 基金项目：西华师范大学科研启动项目（No.11B026）；国家自然科学基金（No.61071162）。 作 者 简 介 ：吴 亚 娟（1974—），女 ，博 士 ，副 教 授 ，研 究 领 域 为 图 像 处 理 和 模 式 识 别 ，E-mail：wuyajuan@cwnu.edu.cn；徐 黎 明 （1991—），男，硕士研究生，研究领域为图像处理。 收稿日期：2016-07-11 修回日期：2016-08-16 文章编号：1002-8331（2017）02-0220-05 

吴亚娟，徐黎明：引入高阶 P-Laplace 的图像全变分盲复原方法 2017，53（2） 221 等人提出了将自回归模型应用到 PSF 的正则约束中，后 用 TV method 复原图像的方法[10]。 国内外许多学者都致力于盲复原算法的研究。有 学者提出了类 TV 函数的正则化约束方法[11]，但忽略了 退化图像平滑区域内的像素值变化，易产生分片常数现 象。结合 Laplace 算子的全变分模型[12]较好地解决了该 问题，但该算法难以平衡收敛性、复杂度和可靠性，且计 算量较大比较耗时。还有学者结合神经网络进行图像 盲反卷积[13]，降低了算法的时间复杂度。此外，高阶扩 散盲复原模型[14]因其较好的平滑扩散性，利用分片平面 图像来近似边界以消除二阶非线性扩散所造成的阶梯 效应，但可能会平滑掉边缘信息。 2 引入高阶 P-Laplace 的全变分盲复原模型 一幅理想图像的边缘部分应具有较好的稀疏特性， 而平滑区域则存在均匀分布和连续平滑渐进的特性。 全变分盲复原方法能保护边缘，而高阶扩散盲复原能较 好地近似平滑区域的变化，消除分片现象以避免阶梯效 应和假边缘情况。为保持良好的边缘性质和平滑渐进， 将四阶的 P-Laplace 算子引入到 TV method 中，复原模 型为：   1 2 h ⊗ u - u α J(uh) = min uh 2 Ω h ⊗ u - u 为 L 的逼近程度。  |Ñ2u|pdxdy  0 2 2 2 其中， 图像 u 0  0 2 2 + α 1 Ω |Ñu|dxdy +  + （1） 范数，表示清晰图像 u 和模糊 |Ñu|dxdy 和  |Ñ2u|pdxdy 均为正 Ω Ω 则化约束项，α 为对应的控制参数，用于控制正则 1 项的权重。 p 为扩散控制因子，由等照度线的曲率 k 和 和 α 2 梯度模值 |Ñu| 共同决定，p 的表达式为：p = 1 + 等照度线的曲率 k = Ñ × Ñu |Ñu| 。 k k + |Ñu| 。 Ω F(xydud 2udnu)dx 对于满足边界条件的泛函 J[u(xy)] 可以定义为： J[u(xy)] =  当 n = 2(Ñ2u) 时，分片平滑的解可以由 n 的高阶扩散 方程得到，并近似于理想图像中平滑区域的像素变化规 律，由此带来较好的视觉感官。特将高阶拉普拉斯扩散因 子  (Ñ2u) pdxdy 引入到全变分盲复原模型中，以抑制振铃 Ω v h h h hv hh (Ñ (Ñ = Ñ + 2Ñ2u + Ñ2u ) p ， vv hv hh 现象和阶梯效应。其中 (Ñ2u) p = (Ñ2u Ñu u) 。 u) ，Ñu = Ñ 全变分盲复原得到的图像拥有较好的客观评价，但 视觉效果不佳，易产生阶梯效应。高阶扩散复原算法由 于其各向同性的特征，使得该类模型可能会平滑掉图像 的边缘细节，导致图像的客观评价不高[15]。式（1）中融入 两种算法的正则项，较好地结合两种复原方法的优势。 3 数值实现 图像盲复原的特性使得事先估计 PSF成为必要操作， 但估计未知信息导致了图像盲复原成为盲反卷积问题 中的一个病态问题，不存在唯一解。正则化方法通过添 加正则化约束项，将该病态问题转化为可求得有限解。 3.1 估计模糊核 首先采用 shock 滤波器 [16]对模糊图像进行边缘预 测，旨在利用双曲线偏微分方程对上述退化模型进行锐 化增强以得出清晰的边缘。因此，根据退化模型可以近 似得出清晰边缘退化成模糊边缘的退化模型： Ñu (xy) = h ⊗ Ñu + n 0 0 其中，Ñu 为退化图像的边缘梯度，Ñu 表示近似的清晰 图像的边缘梯度。将预测得出的清晰图像的边缘梯度 集 Ñu/ 作为先验模型，并引入 h 的 L 范数作为正则项， 估计得到的 PSF 为： hÙ = arg min ||h ⊗ Ñu/ - Ñg||2 + μ||h||2 2 2 uh 为 PSF 的 L 其中，||h ⊗ Ñu/ - Ñg||2 用于估计模糊边缘和清晰边缘 的逼近程度，||h||2 范数，用于抑制 PSF 中的 2 噪声，μ 是 ||h||2 的正则化系数，用于控制该项的权重。 2 根据帕赛伐尔定理，利用快速傅里叶变换（Fast Fourier Transform，FFT）将时间域转换到频率域的点乘运算， 解得： 2 - - - -- --- -- u/)F(¶ F(¶ x - - -- --- -- - u/)F(¶ F(¶ - - - -- --- -- ) + u/)F(¶ F(¶ y - - -- --- -- - u/)F(¶ F(¶ u x 0 u/) + x x y u ) 0 y u/) + μ y ö ÷ ÷ ø æ ç hÙ = F -1 ç è 和 ¶ y x 分别表示水平方向和垂直方向的梯度算 其中，¶ 子。根据 PSF 的非负性，去除 h 中负值。利用预测出的 清晰边缘和 PSF 估计，采用经典图像反卷积算法对图像 清晰部分进行复原，模型定义为： uÙ = arg min ||hÙ ⊗ Ñu - u uh ||2 + η||Ñu - Ñu/||2 0 0 0 ||2 表示模糊图像 u ||hÙ ⊗ Ñu - u 与原始清晰图像 u 的逼 近程度，||Ñu - Ñu/||2 为正则项，η 表示正则项的控制参 数。采用上述方法进行 FFT 操作，求得闭合解为： )F(¶ ü ï ý ï þ 为保证模糊核函数的鲁棒性与预测模糊核的准确 ) + η[ - -- --- - -- ----- F(¶ F(h)F(u x F(h)F(h) + η[ - - -- --- -- ----- F(¶ x -- ----- u/) + - F(¶ y -- ----- ) + - F(¶ )F(¶ y ] u/) y ] ) x )F(¶ uÙ = F -1 )F(¶ ì ï í ï î 0 x y 性，在实验中采用由粗到细的多尺度策略进行估计。 3.2 分裂布雷格曼优化 关于高阶全变分盲复原模型的求解方法很多，文章 采用分裂布雷格曼迭代（Split Bregman Iteration，SBI） 策 略 [17] 和 交 替 最 小 化 迭 代（Alternating Minimization Iteration，AMI）算 法 [9] 进 行 求 解 。 首 先 在 式（1）中 令 = Ñ2u ，后引入两项惩罚项和时间变量，将式 b 1 （1）中的约束模型转化到无约束的最优化模型。定义为： = Ñu ，b 1 

222 2017，53（2） Computer Engineering and Applications 计算机工程与应用 arg min uh   1 2 h ⊗ u - u  2 2 0 + α || + α ||b 1 1 2 ||b 2 ||p +  + - Ñu - t ||2 2 1 + λ 2 2 ||b 2 - Ñ2u - t ||2 2 2 ||b 1 λ 1 2 和 λ 2 为无约束模型中的惩罚项的权重系数，t 其中，λ 1 1 和 t 为用于迭代的时间变量。利用 SBI 算法得到非约 束最优化模型后，再采用 AMI 算法进行求解。具体步 骤如下： 2 （1）初始化。令 n = 1 ，b1 、b1 、t1 1 2 1 ，求解 u 。 （2）固定 b 、b 1 λ un + 1 = arg min 1 1 2 2 、t 、t 1 2 2  h ⊗ u - u  + 0 2 2 u λ 2 2 ||b 2 - Ñ2u - tn ||2 2 2 、t1 2 为 0，u1 = u 。 0 ||b 1 - Ñu - tn ||2 2 1 +  + 其中，h 为分块循环矩阵，对该式求导并采用 FFT 变换 求解可得： un + 1 = ì ï í 0 - -- --- F(h)F(h) + λ ï î 1 （3）解得 u ，固定 t 、t 2 1 - -- --- F(Ñ)F(bn - tn ) + λ 1 1 - -- --- F(Ñ)F(Ñ) + λ - - - ----- F(Ñ2)F(bn 2 2 - - ----- - F(Ñ2)F(Ñ2) - -- --- F(h)F(u ) + λ 1 和 b - tn F -1 。 ü ï ý ï þ ) 2 2 2 ，交替求解 b 1 λ 1 2 λ 2 2 ||b 1 ||b 2 - Ñu(n + 1) - t (n) 1 ||2 2 - Ñu(n + 1) - t (n) 2 ||2 2 n + 1 = arg min b 1 b 1 || +  α ||b 1 1 b 2 n + 1 = arg min  α b 2 ||b 2 2 || + 利用二维迭代收缩（Iterative Shrinkage）函数[18]对 b 1 进行迭代更新。 和 b 和 b ，同样采用 Shrinkage 函数迭代 2 2 （4）解得 u 、b 1 ，解得： 更新 t 和 t 1 t (n + 1) 1 t (n + 1) 2 2 = t (n) 1 = t (n) 2 + Ñu(n + 1) - b(n + 1) + Ñu(n + 1) - b(n + 1) 1 2 3.3 自适应参数 P 值的实现 根据梯度模值 |Ñu| 和曲率 k 的关系可得：p = 1 + (Ñ × Ñu |Ñu| )/(Ñ × Ñu |Ñu| 表示为： + |Ñu|) ，在图像网格示意图（图 1）中可 p = 1 + u u2 y xx - 2u x u u2 y xx 其中： x - 2u u u y xy u u y + u + u xy u2 x u2 yy x + (u2 x yy （2） + u2 y )2 NW W N n u(ij) w s NE E e SE SW 图 1 半点网格示意图 S = u ，¶2u ¶x2 ¶u ¶x 在图 1 中利用逼近思想来离散化式（2），可得： ，¶2u ¶x¶y = u = u xx xy x (u )n ij x = (u )n ij y = (u )n ij xx = (u )n ij yy = (u )n ij xy = un i + 1j un ij + 1 un i + 1j un ij + 1 ij - 1 i - 1j - un 2h - un 2h - 2un ij h2 - 2un ij 2h - 2un ij h2 + un i - 1j + un ij - 1 un i + 1j + 1 + un ij - 1 （3） （4） （5） （6） （7） （8） 将式（4）~（8）带入式（2），便能得到 p 值的具体的离 散化数值表示。 4 实验结果分析 在Inter Core 3.30 GHz/4 GB/Windows 7/Mtalab 7.0 的环境中，对通用测试图（256 像素×256 像素的 Lena/ Cameraman 标准灰度图像）和自带的 8×8 棋盘图像进行 复原。为保证实验的公正性和客观性，所有图像像素值 均归一化到 0~1 之间，迭代次数均为 500 次。复原效果 评价采用主观感受结合客观方法，客观方法[19]用 PSNR （峰值信噪比）来衡量无噪模糊图像，其值越高表示复原 效果越好；利用 MSENS（噪声抑制均方误差）来评价含 噪模糊图像，其值越低代表噪声抑制越充分，复原效果 越好。主观评价[20]则采用 SA 主观分值评价方法。 4.1 参数设置 首先确定合适的 p 值。在图像定点上，梯度模值 |Ñu| 固定，此时扩散因子 p 随 k 值的增大而增大。采用 上述的自适应方式确定合适的 p 值。 2 2 λ 1 和 λ 同文献[9]中对 b 1 的影响相似，λ 取值 越大，Shrinkage 函数迭代更新速度越慢。所有实验中， 统一设定 λ 1 = 10α 1 和 b ，λ 。 采用多尺度策略确定合适的 α 1 = 10-2α 对 TV method 中的正则项影响很大，决定了边缘信息的处理及 扩散程度；参数 α 决定了复原图像过程中平滑区域内 2 高阶扩散的速度。 。参数 α 1 和 α 2 2 2 以图2（a）的复原过程为例，令 α 1 Î[10-5104]，α ' = hα 。 1 1 先采用大尺度步长，令 h = 10 ，结果如图 3 所示。在该范 围内，复原效果由坏变好再变坏，选取一个结果较好的范 Î[10-310-1] ，然后在此范围采用小尺度步长进行复 围 α 1 原。令 h = 2 ，结果如图 4 所示。该图显示当 α = 0.01 ， 1 PSNR 值最大，故选取 α 1 = 0.01 。 利用相同方法确定合适的 α ，取 α 2 = 200 。按照上 2 述方法选取合适的值则能保证复原效果最优。 

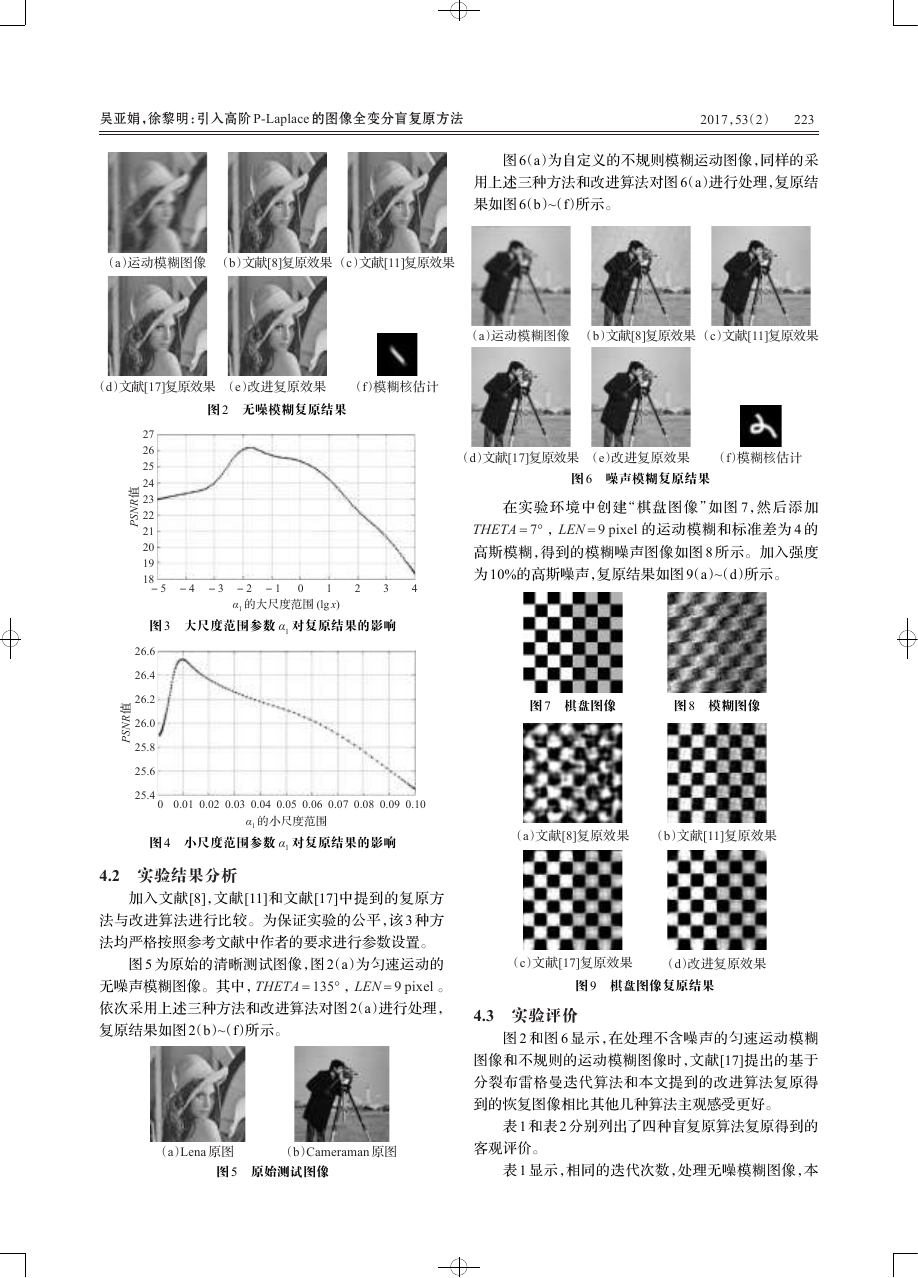
吴亚娟，徐黎明：引入高阶 P-Laplace 的图像全变分盲复原方法 2017，53（2） 223 图 6（a）为自定义的不规则模糊运动图像，同样的采 用上述三种方法和改进算法对图 6（a）进行处理，复原结 果如图 6（b）~（f）所示。 （a）运动模糊图像 （b）文献[8]复原效果 （c）文献[11]复原效果 （d）文献[17]复原效果 （e）改进复原效果 （f）模糊核估计 图 2 无噪模糊复原结果 值 R N S P 27 26 25 24 23 22 21 20 19 18 －5 －4 －3 －2 －1 0 1 2 3 4 的大尺度范围 (lg x) α 1 图 3 大尺度范围参数 α 1 对复原结果的影响 26.6 26.4 26.2 26.0 25.8 25.6 25.4 值 R N S P 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 的小尺度范围 α 1 图 4 小尺度范围参数 α 1 对复原结果的影响 4.2 实验结果分析 加入文献[8]，文献[11]和文献[17]中提到的复原方 法与改进算法进行比较。为保证实验的公平，该 3 种方 法均严格按照参考文献中作者的要求进行参数设置。 图 5 为原始的清晰测试图像，图 2（a）为匀速运动的 无噪声模糊图像。其中，THETA = 135° ，LEN = 9 pixel 。 依次采用上述三种方法和改进算法对图 2（a）进行处理， 复原结果如图 2（b）~（f）所示。 （a）Lena 原图 （b）Cameraman 原图 图 5 原始测试图像 （a）运动模糊图像 （b）文献[8]复原效果 （c）文献[11]复原效果 （d）文献[17]复原效果 （e）改进复原效果 （f）模糊核估计 图 6 噪声模糊复原结果 在实验环境中创建“棋盘图像”如图 7，然后添加 THETA = 7° ，LEN = 9 pixel 的运动模糊和标准差为 4 的 高斯模糊，得到的模糊噪声图像如图 8 所示。加入强度 为 10%的高斯噪声，复原结果如图 9（a）~（d）所示。 图 7 棋盘图像 图 8 模糊图像 （a）文献[8]复原效果 （b）文献[11]复原效果 （c）文献[17]复原效果 （d）改进复原效果 图 9 棋盘图像复原结果 4.3 实验评价 图 2 和图 6 显示，在处理不含噪声的匀速运动模糊 图像和不规则的运动模糊图像时，文献[17]提出的基于 分裂布雷格曼迭代算法和本文提到的改进算法复原得 到的恢复图像相比其他几种算法主观感受更好。 表 1 和表 2 分别列出了四种盲复原算法复原得到的 客观评价。 表 1 显示，相同的迭代次数，处理无噪模糊图像，本 

224 2017，53（2） Computer Engineering and Applications 计算机工程与应用 表 1 Lena 和 Cameraman 降质图像复原结果的 PSNR 和 SA 值比较 图像 Lena Cameraman 算法 文献[8] 文献[11] 文献[17] 改进算法 文献[8] 文献[11] 文献[17] 改进算法 PSNR/dB 29.39 27.62 31.24 33.47 34.55 32.50 35.24 37.75 SA 4 3 3 4 3 3 4 5 表 2 不同强度噪声的棋盘模糊图像复原结果的 PSNR 和 MSENS 值比较表 算法 高斯噪声/% PSNR/dB 文献[8] 文献[11] 文献[17] 改进算法 10 30 60 10 30 60 10 30 60 10 30 60 33.25 24.85 20.84 38.88 32.17 27.30 34.91 28.57 21.43 41.64 36.24 30.09 MSENS 218.47 1 081.40 4 060.50 43.45 322.34 1 078.74 92.98 149.39 761.81 62.38 104.86 350.25 文算法得到的 PSNR 值最高，相比其他几种算法 PSNR 提高了约 7.14%~13.88%。表 2 显示，引入不同强度的噪 声时，改进算法的 PSNR 值最高，MSENS 值也比较理想 （只有在噪声强度为 10%的情况下，改进算法的 MSENS 值略高于文献[11]的算法复原后得到的 MSENS 值）。 5 结束语 以常见的运动模糊为例，将高阶 P-Laplace 算子引入 全变分盲复原模型中，较好地避免了阶梯效应和振铃现 象，对含噪模糊图像的复原达到较理想的效果。同时随 机引入棋盘图像，效果理想，使得改进的复原方法更具 有客观性和一般性。但当图像受到噪声严重污染时，该 方法不能保持在稳定理想的状态，得到的 PSNR 值下降 较快，算法的可靠性与稳定性是文章值得改进的地方。 参考文献： [1] Chan R，Chan T F，Yip A，et al.Numerical methods and applications in total variation image restoration[M].Hand- book of mathematical methods in imaging.New York： Springer，2011：1059-1094. [2] Chaudhuri S，Velmurugan R，Rameshan R.Blind deconvo- International lution methods：a review[M].[S.l.]：Springer Publishing，2014：37-60. [3] 李鑫楠.图像盲复原算法研究[D].长春：吉林大学，2015. [4] Babacan S D，Molina R，Katsaggelos A K，et al.Parameter estimation in TV image restoration using variational dis- tribution approximation[J].IEEE Transactions on Image Processing，2008，17（3）：326-339. [5] Cho S，Lee S.Fast motion deblurring[J].ACM Transactions on Graphics，2009，28（5）：89-97. [6] Xu L，Jia J.Two-phase kernel estimation for robust motion deblurring[C]//European Conference on Computer Vision （ECCV），Greece，2010：81-84. [7] Levin A，Weiss Y，Durand F，et al.Understanding blind decon- volution algorithms[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2011，33（12）：2354-2367. [8] 阮光诗，孙俊喜，孙阳，等.处理异常值的相机抖动模糊图 像复原[J].中国图象图形学报，2014，19（5）：677-682. [9] Chan T F，Wong C.Total variation blind deconvolution[J]. IEEE Transactions on Image Processing，1988，7（3）：370-395. [10] Babacan S D，Molina R，Katsaggelos A K，et al.Varia- tional Bayesian blind deconvolution using a total varia- tion prior[J].IEEE Transactions on Image Processing， 2009，18（1）：12-26. [11] Almeida M S，Almeida L B.Blind and semi-blind de- blurring of natural images[J].IEEE Transactions on Image Processing，2010，19（1）：36-52. [12] Liao H，Ng M K.Blind deconvolution using generalized cross-validation approach to regularization parameter esti- mation[J].IEEE Transactions on Image Processing，2011， 20（3）：670-680. [13] Deng Z，Xia Y.A neural network algorithm for fast blind image restoration using a novel 2D-ARMA parameter estimation[C]//International Conference on Audio Lan- guage and Image Processing（ICALIP），2010：1744-1748. [14] Pang Z，Yang Y.A projected gradient algorithm based on the augmented Lagrangian strategy for image restoration and texture extraction[J].Image and Vision Computing， 2011，29（2/3）：117-126. [15] Cui X，Shi Z，Lin J，et al.The research of image quality assessment methods[J].Physics Procedia，2012：485-491. [16] Money J H，Kang S H.Total variation minimizing blind reference[J].Image and deconvolution with shock filter Vision Computing，2008，26（2）：302-314. [17] Li W，Li Q，Gong W，et al.Total variation blind decon- volution employing split Bregman iteration[J].ELSEVIER Journal of Visual Communication and Image Represen- tation，2012，23（3）：409-417. ℓ [18] Yang A Y，Sastry S S，Ganesh A，et al.Fast 1 minimi- zation algorithms and an application in robust face recog- nition：a review[C]//IEEE International Conference on Image Processing，2010：1849-1852. [19] 赵雪青.降质图像复原方法研究[D].西安：陕西师范大学，2013. [20] Ma L，Li S，Ngan K N，et al.Reduced-reference image quality assessment in reorganized DCT domain[J].Signal Processing：Image Communication，2013，28（8）：884-902.