利用OpenMP/CUDA/MPI对FFT算法优化程序课程报告.pdf

发布时间：2022-06-10 发布人：admin 分类：说明书资料大小：0.32M 资料格式：pdf 举报版权申诉

weixin_44348354-13713152-16359647774394485908.pdf-第1页.png

第1页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第2页.png

第2页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第3页.png

第3页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第4页.png

第4页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第5页.png

第5页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第6页.png

第6页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第7页.png

第7页 / 共12页

weixin_44348354-13713152-16359647774394485908.pdf-第8页.png

第8页 / 共12页

文本预览

Big Integer Multiplication Using Parallel FFT Zhihao Lv January 30, 2020 Abstract The Fast Fourier Transform(FFT) reduce the time complexity of big integer mul- tiplication to Θ(nlogn). However, its parallel implementation is still needed due to the high algorithm constant causing by mass calculation of complex numbers. In this paper we discuss three ways to implement parallel FFT including OpenMP with shared memory, CUDA with cuFFT library and MPI with distributed memory. Details of implementation and runtime comparison is presented in the paper. 1 Introduction 1.1 FFT[2] Fast Fourier transform is the algorithm that calculates the dicrete Fourier transform of secquence X =< X[0],X[1], ...,X[n− 1] > into sequence Y =< Y [0],Y [1], ...,Y [n− 1] > in Θ(nlogn): Y [i] = X[k]ωki i = 0,1, ...,n− 1 (1) n−1 ∑ k=0 Here ω is the primitive nth square root of unity in the complex plane. Assume that n is a power of 2(if not, we can add zero for aligment). Because of the properties of ω, Equation. 1 can be derived into: (n/2)−1 ∑ X[2k]ωki + ωi Y [i] = X[2k + 1]ωki (n/2)−1 ∑ k=0 Here ω is the primitive nth square root of unity in the complex plane. Note that two summation on right side both require a half size calculation compared to the orignal problem, which satisﬁed the divide and conquer strategy. k=0 (2) 1.2 Big Interger Multiplication When numbers in multiplication is bigger 1018, we cannot store them in long long int data type but to design high precision algorithm. Simple simulation with time complexity Θ(nlogn) is too slow for scientiﬁc computing. It is natural to link an integer with a polynomial, for example 234 → 2x3 +3x2 +4. Since the multiplication of polynomials with

the point value representation is Θ(n), we can interpolate two polynomial with ωki by FFT and multiply in Θ(n). When performing the inverse Fourier transform, interpolate with ω−ki: Y1[i] = X1[k]ωki n−1 ∑ k=0 n−1 ∑ k=0 Y2[i] = Z[i] = Y1[i]∗Y2[i] Z[k]ω−ki n−1 ∑ 1 n k=0 X[i] = X2[k]ωki (3) (4) (5) The whole process can be done within Θ(nlogn). 2 Serial Algorithm 2.1 Iterative Algorithm It is not difﬁcult to write a recursive FFT algorithm, but apparently it is too slow and some principles can be found in the recursive process(Figure. 1). For n equals to 2m, when returning to ith level, the calculations are decribe in Equa- Figure 1: Recursive Process tion. 6: 2

Xi[k] = Xi+1[k] + ωkXi+1[k + 2m−i] Xi[k + 2m−i] = Xi+1[k]− ωkXi+1[k + 2m−i] (6) For every pair of two points, it is named as Butterﬂy Operation(Figure. 2). Comparing the sequence at the bottom level and the top level, we can ﬁnd that they Figure 2: Butterﬂy Operation Top(Decimal) Top(Binary) Bottom(Decimal) Bottom(Binary) 0 1 2 3 4 5 6 7 000 001 010 011 100 101 110 111 0 4 2 6 1 5 3 7 000 100 010 110 001 101 011 111 are reverse in bitwise(Table. 1). Table 1: Bitwise Reverse Proposition 2.1 The order of the end level sequence in FFT recursive process is ex- actly the bitwise reverse of the initial order. Therefore, if we swap the position in bitwise, butterﬂy operation can be performed iteratively, thus allowing the feasibility parallel algorithm. 2.2 Serial Code Implementation of bitwise reverse is as Figure. 3. 1 f o r ( i n t i =0; i >1] > >1)|(( i &1)<<(n0−1)); Figure 3: Bitwise Reverse Implementation of FFT is as Figure. 4 3

f o r ( i n t 1 void FFT ( cpx x [ ] , i n t 2 3 4 5 6 7 8 9 10 11 12 13 } } i f ( f ==−1) } 14 } f o r ( i n t f ){ i =0; i

3 OpenMP 3.1 Modiﬁcation of Serial Code Based on multithreading, the main principle of OpenMP is adding preprocessor direc- tive #pragma omp to fork multiple thread and perform the following clause in parallel. The key part for parallelization is the FFT function. Of course, some other part like pre-pocessing will also be parallel if they do not have data dependencies. In the serial code(Figure. 4), we can ﬁnd that variable j and k in two for-loops from line 8 to line 10 actually have no dependency. If we make a copy of array x we can also overcome the data dependencies. f , cpx om [ ] ) { / / f ==1 IDFT , f ==0 DFT f o r shared ( x , pos ) i f ( i

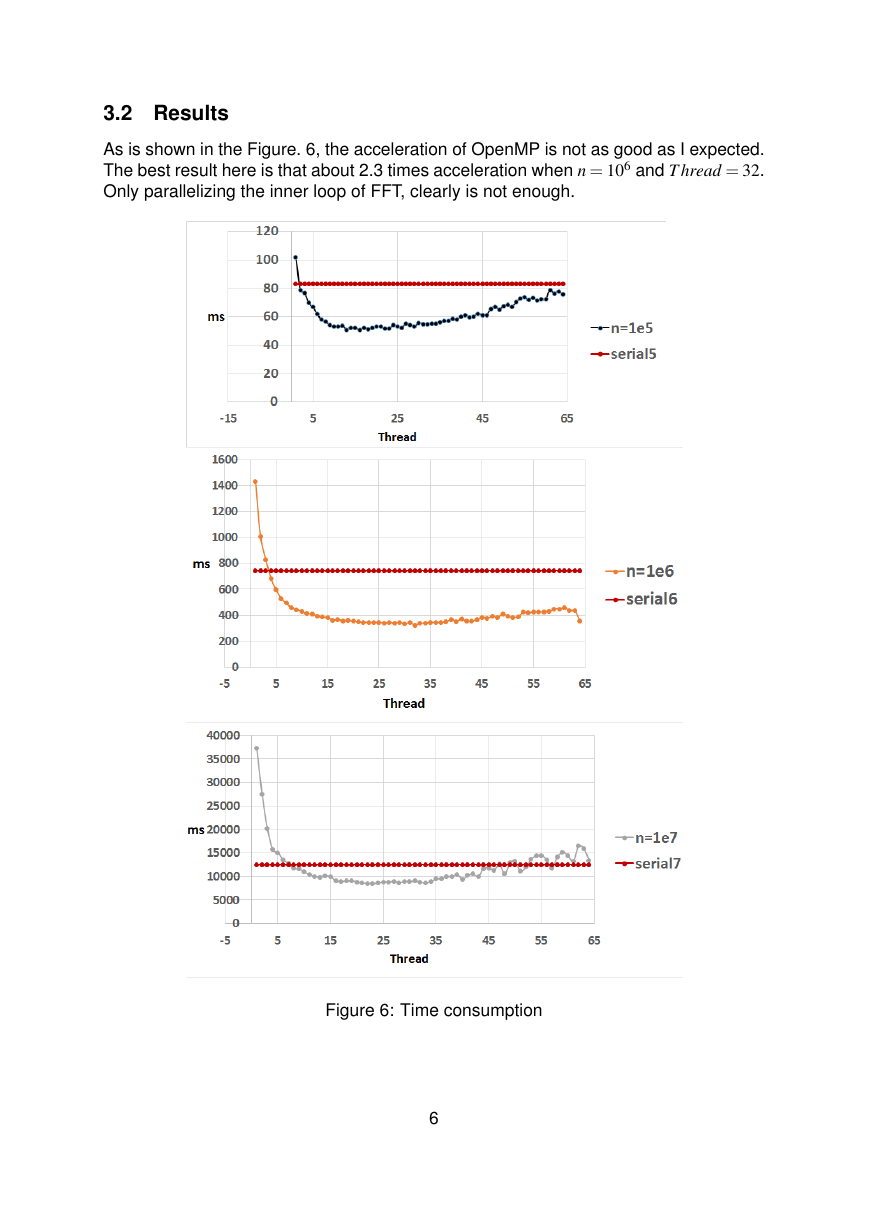
3.2 Results As is shown in the Figure. 6, the acceleration of OpenMP is not as good as I expected. The best result here is that about 2.3 times acceleration when n = 106 and T hread = 32. Only parallelizing the inner loop of FFT, clearly is not enough. Figure 6: Time consumption 6

4 CUDA 4.1 cuFFT The most time-consumption part of FFT is complex number calculation, while GPU computing with SIMD pattern can perfectly solve this problem. However, setting the thread and block number to achieve the best performance could be troublesome so I use CUDA additional library, cuFFT[1], in which the FFT function has been encapsuled and can be used as below(Figure. 7). . . . 1 cudaMalloc ( ( void ∗∗)&a , s i z e ) ; 2 cudaMemcpy ( a , h a , size , cudaMemcpyHostToDevice ) ; 3 4 c u f f t H a n d l e plan ; 5 c u f f t P l a n 1 d (& plan , 6 cufftExecZ2Z ( plan , a , a , CUFFT FORWARD ) ; 7 8 cufftExecZ2Z ( plan , a , a , CUFFT INVERSE ) ; 9 c u f f t D e s t r o y ( plan ) ; t , CUFFT Z2Z , 1 ) ; . . . Figure 7: cuFFT Other computations such as multiplication and convertion of answers from complex to integer are clearly SIMD pattern and can be written in following form(Figure. 8). g l o b a l cufftDoubleComplex ∗b ){ void vector mul ( cufftDoubleComplex ∗a , const const f o r i n t numThreads = blockDim . x ∗ gridDim . x ; i n t ( i n t threadID= b l o c k I d x . x∗ blockDim . x+ threadIdx . x ; i = threadID ; i += numThreads ) { i < T [ 0 ] ; cuDoubleComplex c = cuCmul ( a [ i ] , b [ i ] ) ; a [ i ] = make cuDoubleComplex ( cuCreal ( c ) / T [ 0 ] , cuCimag ( c ) / T [ 0 ] ) ; 1 2 3 4 5 6 7 8 9 } 10 } . . . 11 12 cudaGetDeviceProperties (& prop , 0 ) ; 13 vector mul <<>>(a , b ) ; / prop . maxThreadsPerBlock + 1 , Figure 8: Other kernel functions 7

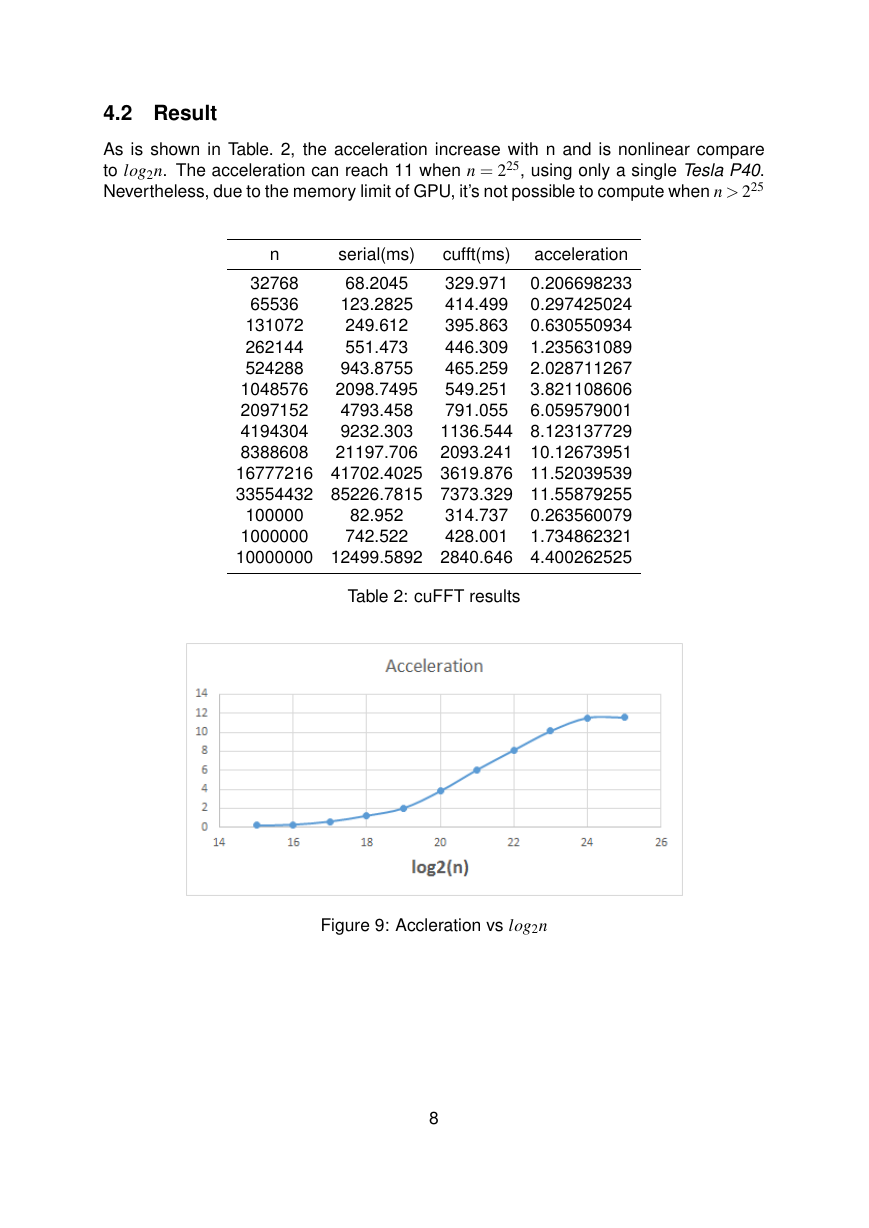
4.2 Result As is shown in Table. 2, the acceleration increase with n and is nonlinear compare to log2n. The acceleration can reach 11 when n = 225, using only a single Tesla P40. Nevertheless, due to the memory limit of GPU, it’s not possible to compute when n > 225 n serial(ms) 68.2045 123.2825 249.612 551.473 943.8755 2098.7495 4793.458 9232.303 21197.706 cufft(ms) acceleration 329.971 0.206698233 32768 414.499 0.297425024 65536 395.863 0.630550934 131072 446.309 1.235631089 262144 465.259 2.028711267 524288 549.251 3.821108606 1048576 791.055 6.059579001 2097152 1136.544 8.123137729 4194304 8388608 2093.241 10.12673951 16777216 41702.4025 3619.876 11.52039539 33554432 85226.7815 7373.329 11.55879255 0.263560079 100000 1000000 1.734862321 10000000 12499.5892 2840.646 4.400262525 82.952 742.522 314.737 428.001 Table 2: cuFFT results Figure 9: Accleration vs log2n 8

分享到：

赞收藏

资料库

利用OpenMP/CUDA/MPI对FFT算法优化程序课程报告.pdf

相关推荐

课程资源

热门标签

最新资料