logo资料库

同步发电机励磁系统控制器的设计与仿真.pdf

发布时间：2022-05-30 发布人：admin 分类：说明书 资料大小：0.43M 资料格式：pdf 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    中国科技论文在线 http://www.paper.edu.cn 同步发电机励磁系统控制器的设计与仿真# 张沈习* （河海大学电气工程系，南京 210098） 摘要：本文先建立了同步发电机励磁系统的数学模型，然后给出了三种同步发电机励磁系统 控制器的设计方法：常规 PID 控制器的设计、模糊 PID 控制器的设计、RBF 神经网络 PID 控 制器的设计，并且用 MATLAB 对在这三种控制器控制下的同步发电机的励磁系统进行了仿真 和对比，得到的结论是：常规 PID 控制效果比较理想，但当发电机系统参数变化或者电力系 统故障时，不能很好地响应参考电压；模糊 PID 在常规 PID 的基础上根据系统控制误差和误 差变化率对系统的 PID 控制参数进行在线修正，从而实现系统更快更好地稳定下来，但其控 制效果仍然受到原 PID 参数的制约；而 RBF 神经网络 PID 控制能够根据系统的控制误差在线 调整各输入量的权值，从而实现系统的自适应控制，而且其适应性极强，只要不陷入局部最 小值，总能很好地控制系统对输入进行响应。 关键词：电力系统；励磁系统；常规 PID；模糊 PID；RBF 神经网络 PID 中图分类号：TM761 Design and Simulation of Synchronous Generator Excitation System Controller Zhang Shenxi (Dept.of Electrical Engineering,Hohai Univercity,NanJing 210098) Abstract: This article first establishes a synchronous generator excitation system model, then gives three kinds of methods to design synchronous generator excitation system controller: conventional PID controller, fuzzy PID controller, RBF neural network PID controller. And uses MATLAB to simulate the excitation system,which is controlled by the three kinds of controller mentioned above.The conclusion comes that:The conventional PID controller’s results will be ideal, but when the generator’s parameters varies or power system fails,it cannot give a good response to the reference voltage;The fuzzy PID controller is in the basis of conventional PID controller ,it can revise the PID control parameters of the system on line according to the system error and error change rate. It can achieve faster and better stability of the system, but its effect is still under the constraints of PID parameters;The RBF neural network PID controller can adjust the input weights online to achieve adaptive control according to the system error.As long as not falling into local minimum, it always has a good response to the input with its highly adaptable. Keywords:Power system;Excitatin system;Conventional PID;Fuzzy PID;RBF neural network PID 0 引言 同步发电机励磁控制系统是非线性、参数时变、要求响应速度快的实时闭环反馈控制系 统，对励磁自动控制系统提出了较高的控制要求。虽然研究励磁控制己有多种方法，取得了 不少成果，但尚存在相应的问题。随着新技术和新理论的发展，开辟智能型的最优励磁控制 系统是发展方向。励磁控制方式的发展是随着控制理论的发展而发展的，从上个世纪 40 年 代至今，主要经过了以下几个发展阶段[1]：古典励磁控制方式、强力式励磁控制、线性最优 励磁控制、非线性励磁控制自适应励磁控制、智能励磁控制。以上每种控制策略在解决某一 方面的问题时有着良好的效果，但是往往在设计或控制过程中都有难以解决的问题。因此， 基金项目：河海大学大学生创新计划训练 作者简介：张沈习（1988-），男，本科生，主要研究方向：电力系统建模，控制系统的设计. E-mail: willzsx@163.com - 1 -
    中国科技论文在线 http://www.paper.edu.cn 如果将这些控制方法结合起来，最大限度的发挥这些控制方法的优点，并尽量避免它们的不 足，将会把电力系统的励磁控制推到一个全新的阶段。 本文研究的目的是得到常规 PID 控制器控制下的同步电机励磁特性、模糊 PID 控制器 控制下的同步电机励磁特性和 RBF 神经网络 PID 控制器控制下的同步电机励磁特性，并对 三种控制策略进行比较和分析。 1 励磁系统数学模型 由于不考虑发电机的内部状态变化，且不考虑辅助控制信号，则励磁系统为单输入单输 出系统，所以本文采用简化的传递函数来表征系统各个组成部分的数学模型[2]。 1.1 同步发电机传递函数 同步发电机的传递函数是非常复杂的，但如果只研究励磁系统的动态特性时，同步发电 机的传递函数可以简化为一阶滞后环节： G s ( ) G = K G T s + d 0 1 (1) 其中， GK 表示发电机的放大系数， 0dT 表示其时间常数，忽略发电机磁场饱和现象。 1.2 电压测量和比较单元传递函数 测量比较单元的传递函数可用下式表示： G s ( ) R = de U s ( ) U s ( ) G = K R T s + R 1 (2) 其中， deU 表示测量比较单元的输出信号， GU 表示机端电压， RK 表示电压比例系数， RT 表示测量回路的时间常数。 1.3 移相触发单元及功率单元传递函数 最大可能滞后的时间可由下式确定: zT = 1 mf (3) 其中， m 表示整流电路控制的相数， f 表示电源的频率。 因此，包括触发器和晶闸管整流器的移相触发单元及功率单元的传递函数为： G s ( ) = u s ( ) d s u ( ) SM = K z ⎡ ⎢ ⎢ ⎢ ⎣ 1 + T s z + 1 1 2 T s 2 2 z + ... ⎤ ⎥ ⎥ ⎥ ⎦ (4) 式中， du 为功率单元的输出， zK 为 du 和 SMu 之间的放大系数。略去高次项就得到简 化后的传递函数为: G z = K z T s + z 1 (5) 这样，就得到了同步发电机励磁控制系统各部分的传递函数，从而可以得到整个控制系 统的模型。 - 2 -
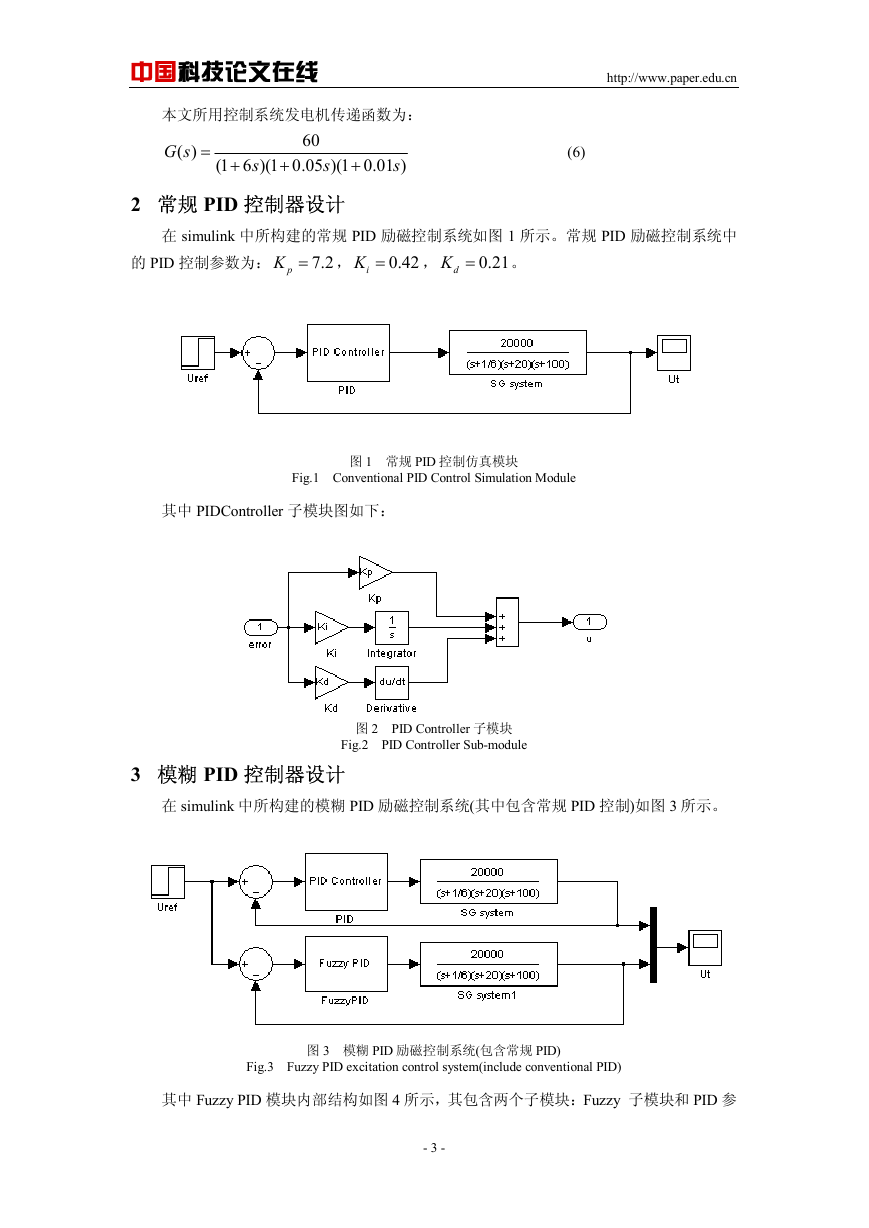
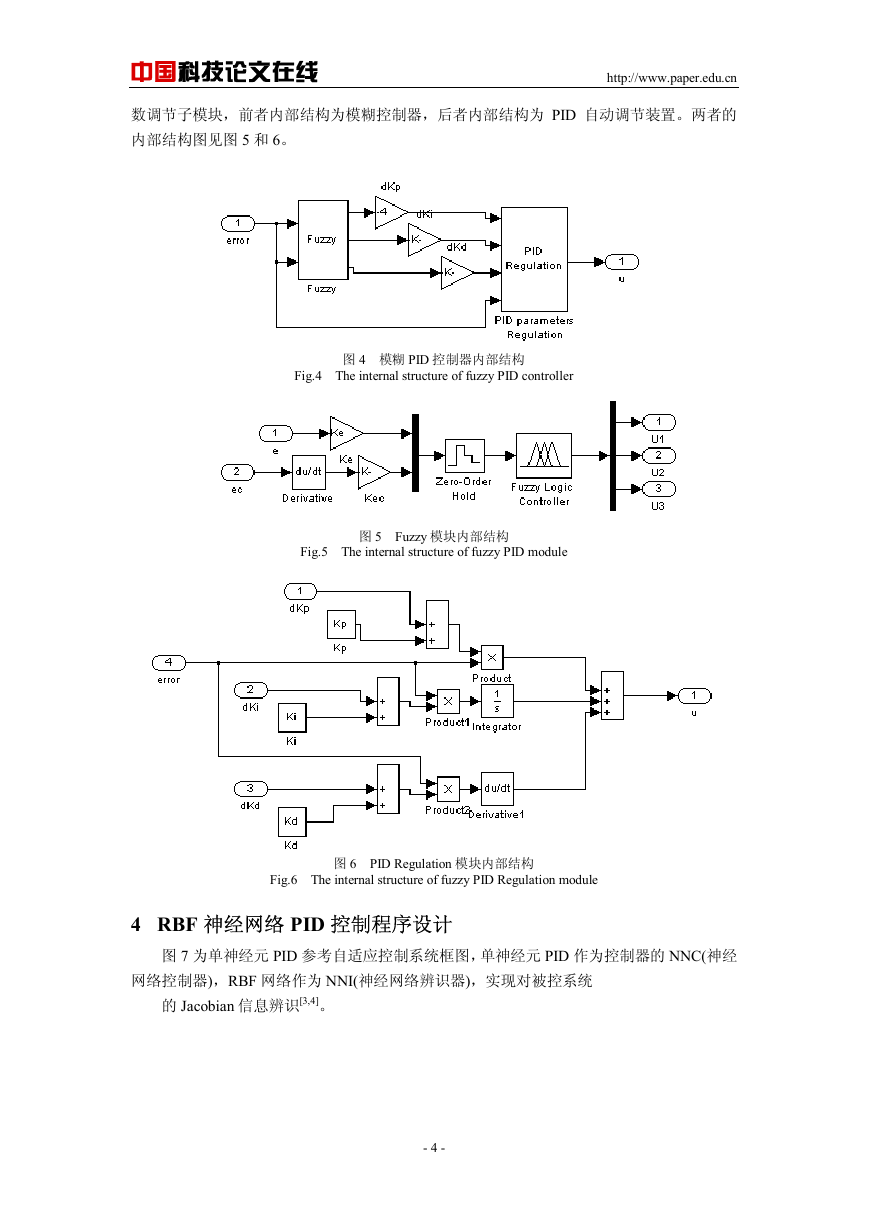
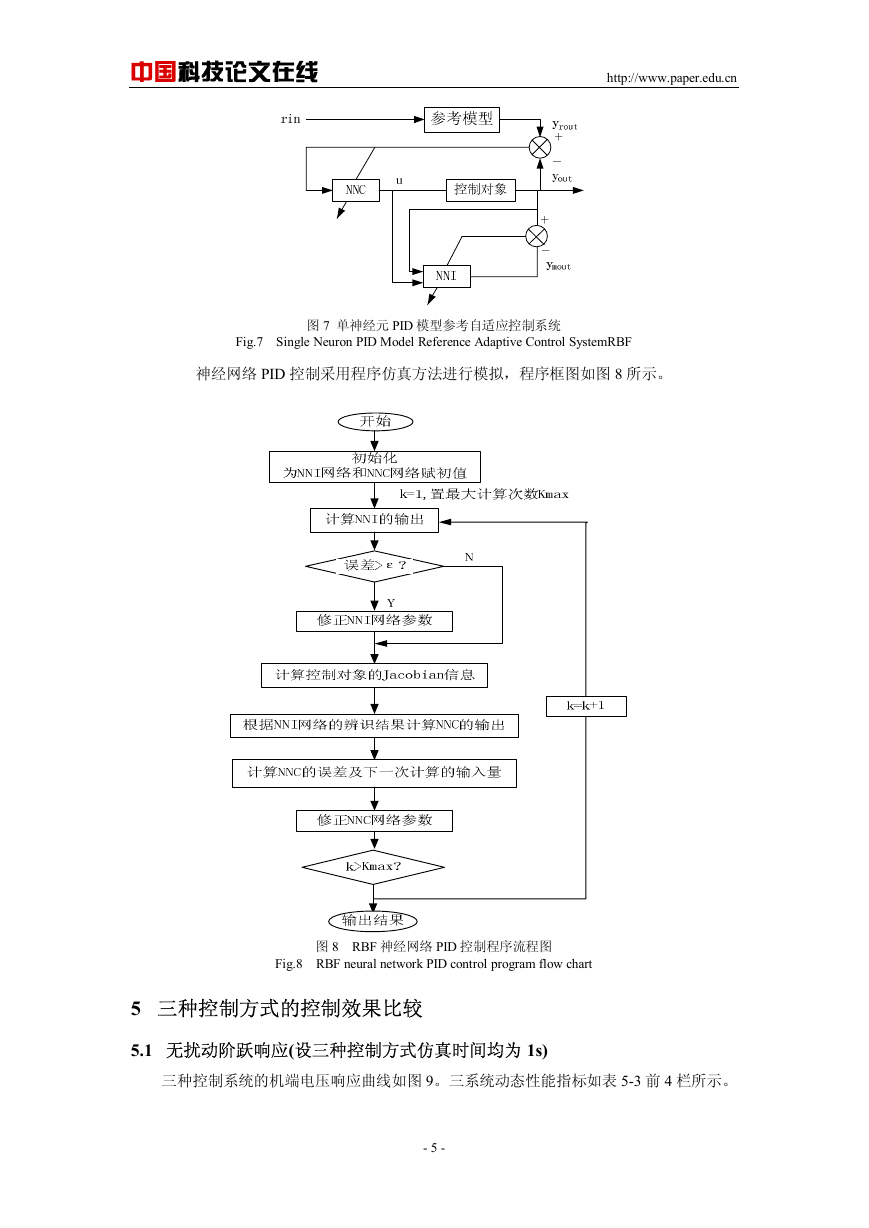
    中国科技论文在线 http://www.paper.edu.cn 本文所用控制系统发电机传递函数为： G s ( ) = 60 s (1 6 )(1 0.05 )(1 0.01 ) + + s s + (6) 2 常规 PID 控制器设计 在 simulink 中所构建的常规 PID 励磁控制系统如图 1 所示。常规 PID 励磁控制系统中 的 PID 控制参数为： pK = ， 7.2 iK = 0.42 ， dK = 0.21 。 图 1 常规 PID 控制仿真模块 Fig.1 Conventional PID Control Simulation Module 其中 PIDController 子模块图如下： 图 2 PID Controller 子模块 Fig.2 PID Controller Sub-module 3 模糊 PID 控制器设计 在 simulink 中所构建的模糊 PID 励磁控制系统(其中包含常规 PID 控制)如图 3 所示。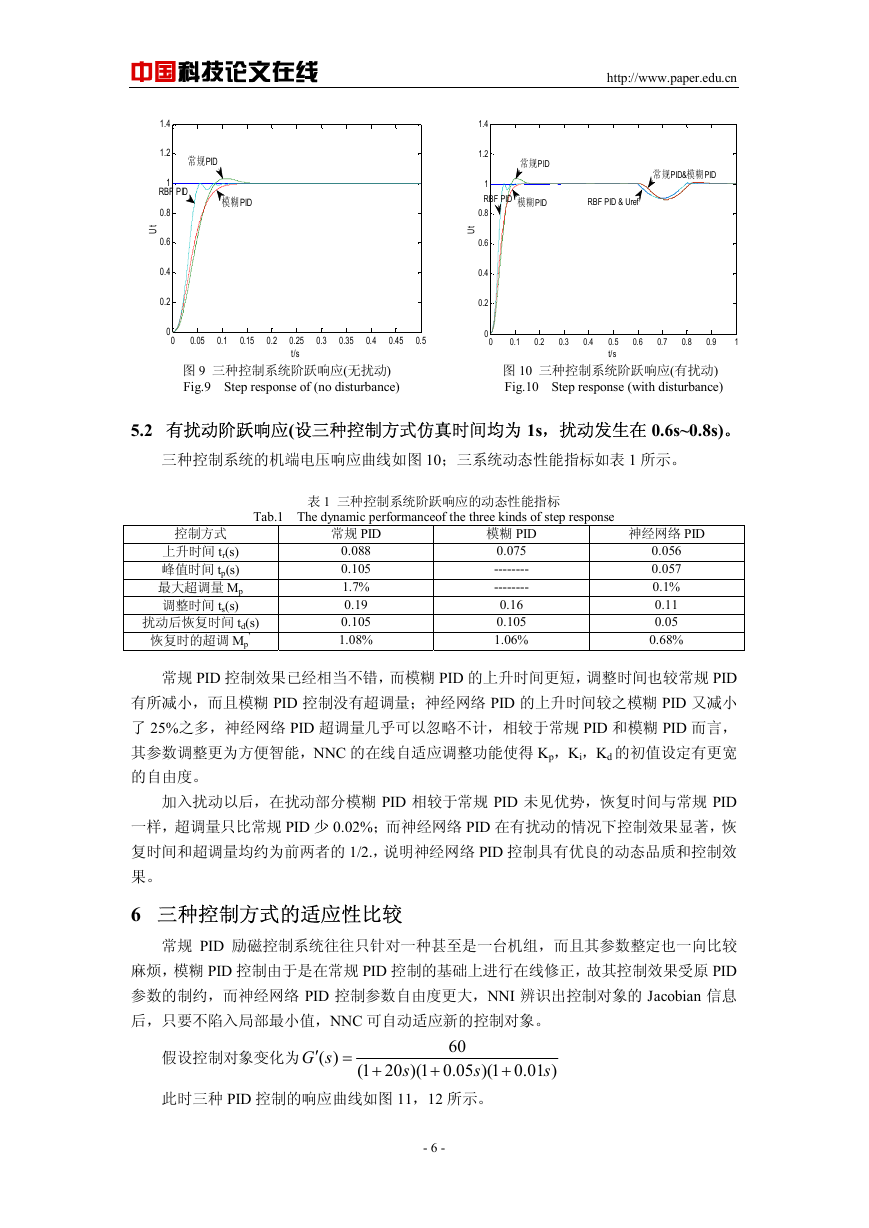 图 3 模糊 PID 励磁控制系统(包含常规 PID) Fig.3 Fuzzy PID excitation control system(include conventional PID) 其中 Fuzzy PID 模块内部结构如图 4 所示，其包含两个子模块：Fuzzy 子模块和 PID 参 - 3 -
    中国科技论文在线 http://www.paper.edu.cn 数调节子模块，前者内部结构为模糊控制器，后者内部结构为 PID 自动调节装置。两者的 内部结构图见图 5 和 6。 图 4 模糊 PID 控制器内部结构 Fig.4 The internal structure of fuzzy PID controller 图 5 Fuzzy 模块内部结构 Fig.5 The internal structure of fuzzy PID module 图 6 PID Regulation 模块内部结构 Fig.6 The internal structure of fuzzy PID Regulation module 4 RBF 神经网络 PID 控制程序设计 图 7 为单神经元 PID 参考自适应控制系统框图，单神经元 PID 作为控制器的 NNC(神经 网络控制器)，RBF 网络作为 NNI(神经网络辨识器)，实现对被控系统 的 Jacobian 信息辨识[3,4]。 - 4 -
    中国科技论文在线 http://www.paper.edu.cn 图 7 单神经元 PID 模型参考自适应控制系统 Fig.7 Single Neuron PID Model Reference Adaptive Control SystemRBF 神经网络 PID 控制采用程序仿真方法进行模拟，程序框图如图 8 所示。 图 8 RBF 神经网络 PID 控制程序流程图 Fig.8 RBF neural network PID control program flow chart 5 三种控制方式的控制效果比较 5.1 无扰动阶跃响应(设三种控制方式仿真时间均为 1s) 三种控制系统的机端电压响应曲线如图 9。三系统动态性能指标如表 5-3 前 4 栏所示。 - 5 -
    中国科技论文在线 http://www.paper.edu.cn 1.4 1.2 常规PID 1 RBF PID 模糊PID t U 0.8 0.6 0.4 0.2 0 0 1.4 1.2 1 RBF PID 0.8 t U 常规PID 常规PID&模糊PID 模糊PID RBF PID & Uref 0.6 0.4 0.2 0 0 0.1 0.2 0.3 0.4 0.5 t/s 0.6 0.7 0.8 0.9 1 0.05 0.1 0.15 0.2 0.25 t/s 0.3 0.35 0.4 0.45 0.5 图 9 三种控制系统阶跃响应(无扰动) 图 10 三种控制系统阶跃响应(有扰动) Fig.9 Step response of (no disturbance) Fig.10 Step response (with disturbance) 5.2 有扰动阶跃响应(设三种控制方式仿真时间均为 1s，扰动发生在 0.6s~0.8s)。 三种控制系统的机端电压响应曲线如图 10；三系统动态性能指标如表 1 所示。 表 1 三种控制系统阶跃响应的动态性能指标 Tab.1 The dynamic performanceof the three kinds of step response 模糊 PID 神经网络 PID 控制方式 上升时间 tr(s) 峰值时间 tp(s) 最大超调量 Mp 调整时间 ts(s) 扰动后恢复时间 td(s) ’ 恢复时的超调 Mp 常规 PID 0.088 0.105 1.7% 0.19 0.105 1.08% 0.075 -------- -------- 0.16 0.105 1.06% 0.056 0.057 0.1% 0.11 0.05 0.68% 常规 PID 控制效果已经相当不错，而模糊 PID 的上升时间更短，调整时间也较常规 PID 有所减小，而且模糊 PID 控制没有超调量；神经网络 PID 的上升时间较之模糊 PID 又减小 了 25%之多，神经网络 PID 超调量几乎可以忽略不计，相较于常规 PID 和模糊 PID 而言， 其参数调整更为方便智能，NNC 的在线自适应调整功能使得 Kp，Ki，Kd 的初值设定有更宽 的自由度。 加入扰动以后，在扰动部分模糊 PID 相较于常规 PID 未见优势，恢复时间与常规 PID 一样，超调量只比常规 PID 少 0.02%；而神经网络 PID 在有扰动的情况下控制效果显著，恢 复时间和超调量均约为前两者的 1/2.，说明神经网络 PID 控制具有优良的动态品质和控制效 果。 6 三种控制方式的适应性比较 常规 PID 励磁控制系统往往只针对一种甚至是一台机组，而且其参数整定也一向比较 麻烦，模糊 PID 控制由于是在常规 PID 控制的基础上进行在线修正，故其控制效果受原 PID 参数的制约，而神经网络 PID 控制参数自由度更大，NNI 辨识出控制对象的 Jacobian 信息 后，只要不陷入局部最小值，NNC 可自动适应新的控制对象。 假设控制对象变化为 G s ( ) ′ = 60 s (1 20 )(1 0.05 )(1 0.01 ) + + + s s 此时三种 PID 控制的响应曲线如图 11，12 所示。 - 6 -
    中国科技论文在线 http://www.paper.edu.cn 1.4 1.2 ??PID 1 RBF PID ??PID ??PID&??PID RBF PID & Uref RBF PID 模糊PID 常规PID 1.4 1.2 1 0.8 0.6 0.4 0.2 t U 0 0 0.05 0.1 0.15 0.2 0.3 0.35 0.4 0.45 0.5 0.25 t/s Ut 0.8 0.6 0.4 0.2 0 0 控制方式 上升时间 tr(s) 峰值时间 tp(s) 最大超调量 Mp 调整时间 ts(s) 0.1 0.2 0.3 0.4 0.5 t/s 0.6 0.7 0.8 0.9 1 图 11 三种控制响应曲线(无扰动) 图 12 三种控制响应曲线(有扰动) Response curves of control (no disturbance) Response curves of control (with disturbance) 为画图方便，图 12 中的扰动由 0.6~0.8s 调整为 05~0.7s。系统调整时间由原先的不到 0.2s 变为接近 0.4s，超调量也从 1.7%上升为 4.04%。 表 2 发电机系统参数变化后三种控制系统阶跃响应的动态性能指标 Tab.2 The three kinds of dynamic step response performance after the parameters changed 模糊 PID 神经网络 PID 常规 PID 0.135 0.177 5.22% 0.395 0.155 0.85% 0.126 0.168 4.96% 0.290 0.155 0.84% 0.116 0.122 4.70% 0.147 0.05 0.13% 扰动后恢复时间 td(s) ’ 恢复时的超调 Mp 注：前 4 栏数据为无扰动的情况，有扰动增加了第 5，6 栏 控制响应曲线如图 11，12。发电机参数变化前模糊控制无超调量，而现在模糊 PID 控 制产生 3.95%的超调量，且调整时间也随着常规 PID 控制成倍增加；而神经网络 PID 控制系 统依然保持着它卓越的控制能力和动态特性，如表 2 所示，无论是在系统响应时间还是超调 量，抑或是干扰情况下的响应，神经网络这种智能控制方法都表现出它的强大。 7 结论 1、常规 PID 控制效果虽然比较理想，但是当发电机系统参数变化或者电力系统故障时， 不能很好地响应参考电压； 2、模糊 PID 控制在常规 PID 参数的基础上根据系统控制误差和误差变化率对系统的 PID 参数进行在线修正，从而使系统更快更好地稳定，但其控制效果仍受到原 PID 参数的制约； 3、RBF 神经网络 PID 控制能够根据系统的控制误差在线调整各输入量的权值，从而实 现控制系统的自适应控制，其适应性极强，只要不陷入局部最小值，总能很好地控制励磁系 统对输入进行响应。 [参考文献]（References） [1] 韦皓. 基于模糊神经网络的发电机 PID 励磁控制研究[D]. 硕士学位论文, 广西大学, 2007. [2] 杨永灯. 同步发电机模糊自调整 PID 励磁控制策略研究[D].硕士学位论文, 西安理工大学, 2006. [3] 刘金堒. 先进 PID 控制及其 MATLAB 仿真[M]. 北京: 电子工业出版社,2003 年 1 月. [4] 李小凡. 基于 RBF 神经网络整定的 PID 控制器设计[J]. 兵工自动化,2009 年 1 月, 第 28 卷第 1 期. [5] 石辛民,郝整清. 模糊控制及其 MATLAB 仿真[M]. 北京: 清华大学出版社,北京交通大学出版社, 2008 年 3 月. [6] 龙云. 同步发电机励磁调节参数优化[D]. 硕士学位论文, 浙江大学, 2003. - 7 -
    分享到：
    赞 收藏

    相关推荐

    资料库

    开发技术

    共收录19306份资料，累计14个分类，关注成员有19位，主要包括：Actionscript,Javascript,PHP,VB,Perl,Delphi,Python,C#,C,Java,C++,Web开发,硬件开发,其它

    热门标签

    Actionscript Javascript PHP VB Perl Delphi Python C# C Java C++ Web开发 硬件开发 其它

    最新资料