悬链线方程的推导 一根无比柔软的绳子，两固定，自然静止状态下，它的形状是悬链线。其实曲线是以绳 子命名的。如何根据绳子的受力来推导出悬链线方程呢？用高等数学所学的知识就够了。 第一步：背景知识 ㈠我们熟悉如何将 sin(   n  ) 2 转化成余弦的形式，口诀是奇变偶不变，符号看象限。 现在扩展一下，研究正切、余切，正割、余割的转化口诀。 tanx cotx 转换：奇变号变偶不变。也就是说，n 为奇数时，要转化成相反形式，且要 补一个负号，n 为偶数时就不用变了。 secx cscx 转换：奇变偶不变，符号看象限。我正弦、余弦非常相似。 ㈡不定积分 csc xdx    dx sin x    ln csc x  cot Cx    dx x 2 cos x 2 sin2 sec 2 xdx 2 2 x tan 2   d x tan 2 x 2 tan  ln tan Cx  2 sec xdx    dx cos x    ln sec x  tan Cx  ( xd  sin( x   ) 2  ) 2  ln csc( x   ) 2  cot( x   ) 2  C ，令 x  a tan t ，   2  t  2   sec tdt  ln sec t  tan Ct   C  ln( x  2 x  2 a )  C 1 求    ln CC 1  x a 2 a x dx 2  2 a 2 sec tan 2 a  a ln  a 2 2 tdt at  2 x a  

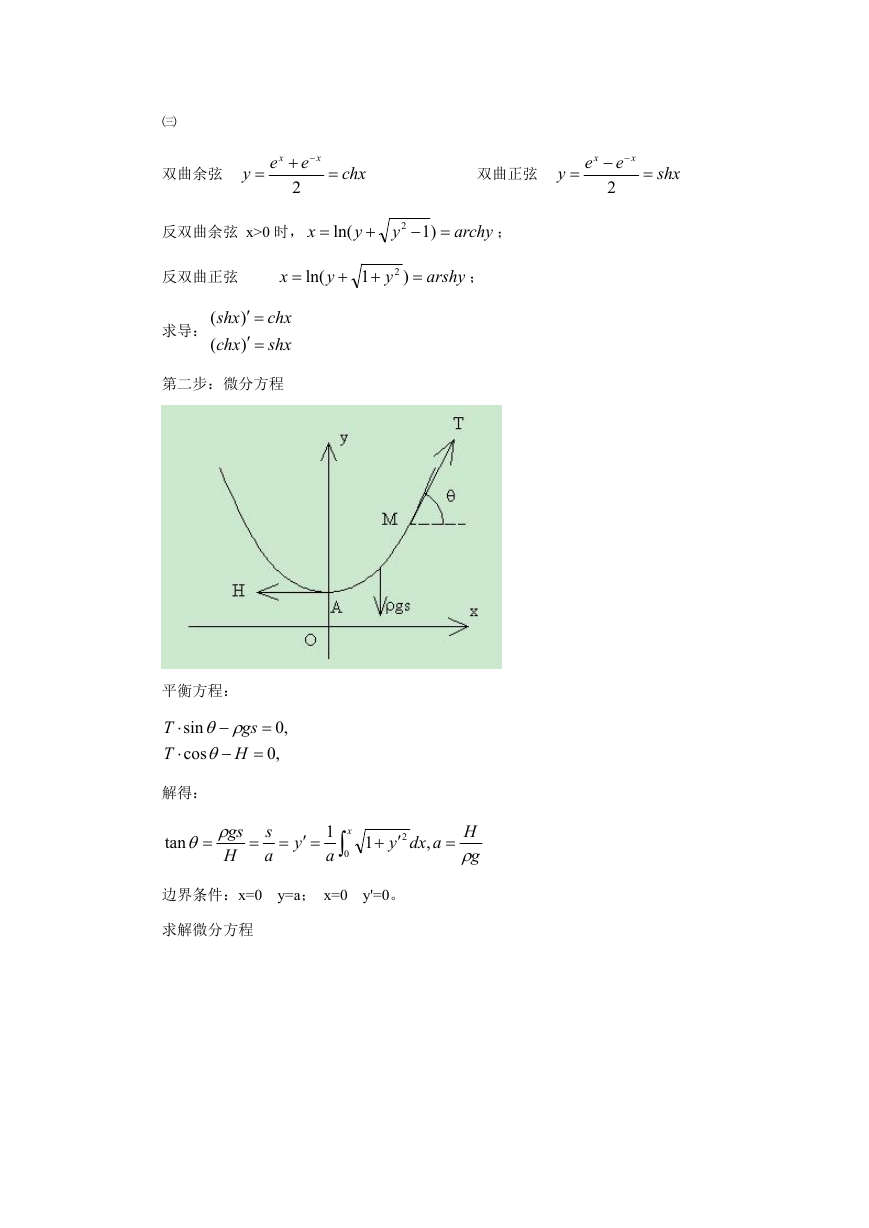
㈢ 双曲余弦 y  x e  x e  2  chx 双曲正弦 y  x e  x e  2  shx 反双曲余弦 x>0 时， x  ln( y  2 y  )1  archy ； 反双曲正弦 x  ln( y  1  2 y )  arshy ； 求导： ( ( shx chx  )  ) chx shx 第二步：微分方程 平衡方程： T T   sin cos ,0 gs    ,0 H    解得： tan   gs  H  s a  y 1 a x  0 1  y 2 Hadx , g   边界条件：x=0 y=a； x=0 y'=0。 求解微分方程 

y    11 a dp 1 p  dp 1 p  2 2 d p d x  11 a  2 p 2  y , 令 y  p ，则 y    1 a 1 a  dx dx 解得 : ln( p  2 p  )1  1 a Cx  1 把 p x  0 代入，得 C 1  ,0 arshp  1 a x arshp Cx  1  1 a 0  )1( x a )1( sh x a )1( x a  sh  a ( a sh p  sh dy dx dy   dy   把 y x  0 xd x ) ( a a xcha   a sha  xd a C 2  y dx x a ) 代入，得 C 2  ,0 y xcha  a x a ea   x a e  2