郑君里《信号与系统》（第3版）笔记和课后习题（含考研真题）详解.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书资料大小：34.19M 资料格式：pdf 举报版权申诉

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第1页.png

第1页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第2页.png

第2页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第3页.png

第3页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第4页.png

第4页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第5页.png

第5页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第6页.png

第6页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第7页.png

第7页 / 共404页

f5715728-c33f-478a-9b26-58c4501854a8.pdf-第8页.png

第8页 / 共404页

目　录

第1章　绪　论

1.1　复习笔记

1.2　课后习题详解

1.3　名校考研真题详解

第2章　连续时间系统的时域分析

2.1　复习笔记

2.2　课后习题详解

2.3　名校考研真题详解

第3章　傅里叶变换

3.1　复习笔记

3.2　课后习题详解

3.3　名校考研真题详解

第4章　拉普拉斯变换、连续时间系统的s域分析

4.1　复习笔记

4.2　课后习题详解

4.3　名校考研真题详解

第5章　傅里叶变换应用于通信系统——滤波、调制与抽样

5.1　复习笔记

5.2　课后习题详解

5.3　名校考研真题详解

第6章　信号的矢量空间分析

6.1　复习笔记

6.2　课后习题详解

6.3　名校考研真题详解

第7章　离散时间系统的时域分析

7.1　复习笔记

7.2　课后习题详解

7.3　名校考研真题详解

第8章　z变换、离散时间系统的z域分析

8.1　复习笔记

8.2　课后习题详解

8.3　名校考研真题详解

第9章　离散傅里叶变换以及其他离散正交变换

9.1　复习笔记

9.2　课后习题详解

9.3　名校考研真题详解

第10章　模拟与数字滤波器

10.1　复习笔记

10.2　课后习题详解

10.3　名校考研真题详解

第11章　反馈系统

11.1　复习笔记

11.2　课后习题详解

11.3　名校考研真题详解

第12章　系统的状态变量分析

12.1　复习笔记

12.2　课后习题详解

12.3　名校考研真题详解

目录第 1 章绪论 ........................................................................................................................................................... 5 1.1 复习笔记 ...................................................................................................................................................... 5 1.2 课后习题详解 .............................................................................................................................................. 7 1.3 名校考研真题详解 .................................................................................................................................... 23 第 2 章连续时间系统的时域分析 ......................................................................................................................... 25 2.1 复习笔记 .................................................................................................................................................... 25 2.2 课后习题详解 ............................................................................................................................................ 27 2.3 名校考研真题详解 .................................................................................................................................... 53 第 3 章傅里叶变换 ................................................................................................................................................. 56 3.1 复习笔记 .................................................................................................................................................... 56 3.2 课后习题详解 ............................................................................................................................................ 59 3.3 名校考研真题详解 .................................................................................................................................. 102 第 4 章拉普拉斯变换、连续时间系统的 s 域分析 ........................................................................................... 107 4.1 复习笔记 .................................................................................................................................................. 107 4.2 课后习题详解 .......................................................................................................................................... 110 4.3 名校考研真题详解 .................................................................................................................................. 157 第 5 章傅里叶变换应用于通信系统——滤波、调制与抽样 ........................................................................... 164 5.1 复习笔记 .................................................................................................................................................. 164 5.2 课后习题详解 .......................................................................................................................................... 166 5.3 名校考研真题详解 .................................................................................................................................. 185 第 6 章信号的矢量空间分析 ............................................................................................................................... 192 6.1 复习笔记 .................................................................................................................................................. 192 6.2 课后习题详解 .......................................................................................................................................... 194 6.3 名校考研真题详解 .................................................................................................................................. 218 第 7 章离散时间系统的时域分析 ....................................................................................................................... 220 7.1 复习笔记 .................................................................................................................................................. 220 7.2 课后习题详解 .......................................................................................................................................... 222 7.3 名校考研真题详解 .................................................................................................................................. 246 第 8 章 z 变换、离散时间系统的 z 域分析 ........................................................................................................ 249 8.1 复习笔记 .................................................................................................................................................. 249 8.2 课后习题详解 .......................................................................................................................................... 252 8.3 名校考研真题详解 .................................................................................................................................. 283 第 9 章离散傅里叶变换以及其他离散正交变换 ............................................................................................... 287 9.1 复习笔记 .................................................................................................................................................. 287 9.2 课后习题详解 .......................................................................................................................................... 289 9.3 名校考研真题详解 .................................................................................................................................. 314 第 10 章模拟与数字滤波器 ................................................................................................................................. 317 10.1 复习笔记 ................................................................................................................................................ 317 10.2 课后习题详解 ........................................................................................................................................ 319 10.3 名校考研真题详解 ................................................................................................................................ 346 第 11 章反馈系统 ................................................................................................................................................. 353 11.1 复习笔记 ................................................................................................................................................ 353 11.2 课后习题详解 ........................................................................................................................................ 355 11.3 名校考研真题详解 ................................................................................................................................ 381 第 12 章系统的状态变量分析 ............................................................................................................................. 385 12.1 复习笔记 ................................................................................................................................................ 385 12.2 课后习题详解 ........................................................................................................................................ 386 12.3 名校考研真题详解 ................................................................................................................................ 406

第 1 章绪论 1.1 复习笔记一、信号信号是消息的表现形式和载体，消息是信号的具体内容。信号从不同角度可以分为四类：（1）确定性信号与随机信号；（2）周期信号和非周期信号；（3）连续时间信号与离散时间信号；（4）一维信号与多维信号。 1．典型的连续信号（1）指数信号：（2）正弦信号：（3）复指数信号：（4）抽样信号：（5）钟形信号(高斯函数)： 2．信号的运算（1）时移（2）反褶（3）尺度变换，若，则的波形沿时间轴向左移动；反之，则向右移动。，把的波形以为轴反褶过来。 ( 为正实系数)，若，则的波形沿时间轴被压缩；反之，则被扩展。 3．阶跃函数和冲激函数（1）单位阶跃信号在跳变点处，函数值未定义，或在处规定函数值。（2）单位冲激信号冲激函数的性质 (),atftKeaR()sin()ftKt()()stjtftKeKesin()tSatt2()()tftEe0()()ftftt00t()ft()()ftft()ft0t()()ftfata1a()ft()ut0,0()1,0tutt0t0t1(0)2u()t()1()0,0tdttt

①抽样性： ②奇偶性： ③尺度运算： ④微积分性质： ⑤冲激偶： ⑥卷积性质： 4．信号的分解（1）直流分量＋交流分量：（2）偶分量＋奇分量：其中，偶分量：；奇分量：。（3）脉冲分量的叠加冲激信号的叠加：阶跃信号的叠加：（较少用）（4）实部分量+虚部分量瞬时值为复数的信号 f(t)可分解为：（5）正交函数分量的叠加：如傅里叶级数。二、系统系统是由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。 1．系统的分类根据数学模型的差异来划分，系统分为：（1）连续时间系统和离散时间系统；（2）线性系统和非线性系统；（3）时变系统和时不变系统；（4）集总参数系统和分布参数系统；（5）可逆系统和不可逆系统；（6）即时系统和动态系统。 2．线性时不变系统的基本特性输入 f(t) 系统输出 y(t) ()()()(0)(0)()(0)tftdttfdtftdtf()()tt1()()atta()(),()()tdtutdutdt''()()(0)tftdtf'()0tdt()()()fttft()()()DAftftft11()[()()][()()]22ftftftftft1()[()()]2eftftft1()[()()]2oftftft111()()()ftftttdt11101()()(0)()()dftftfututtdtdt()()()riftftjft

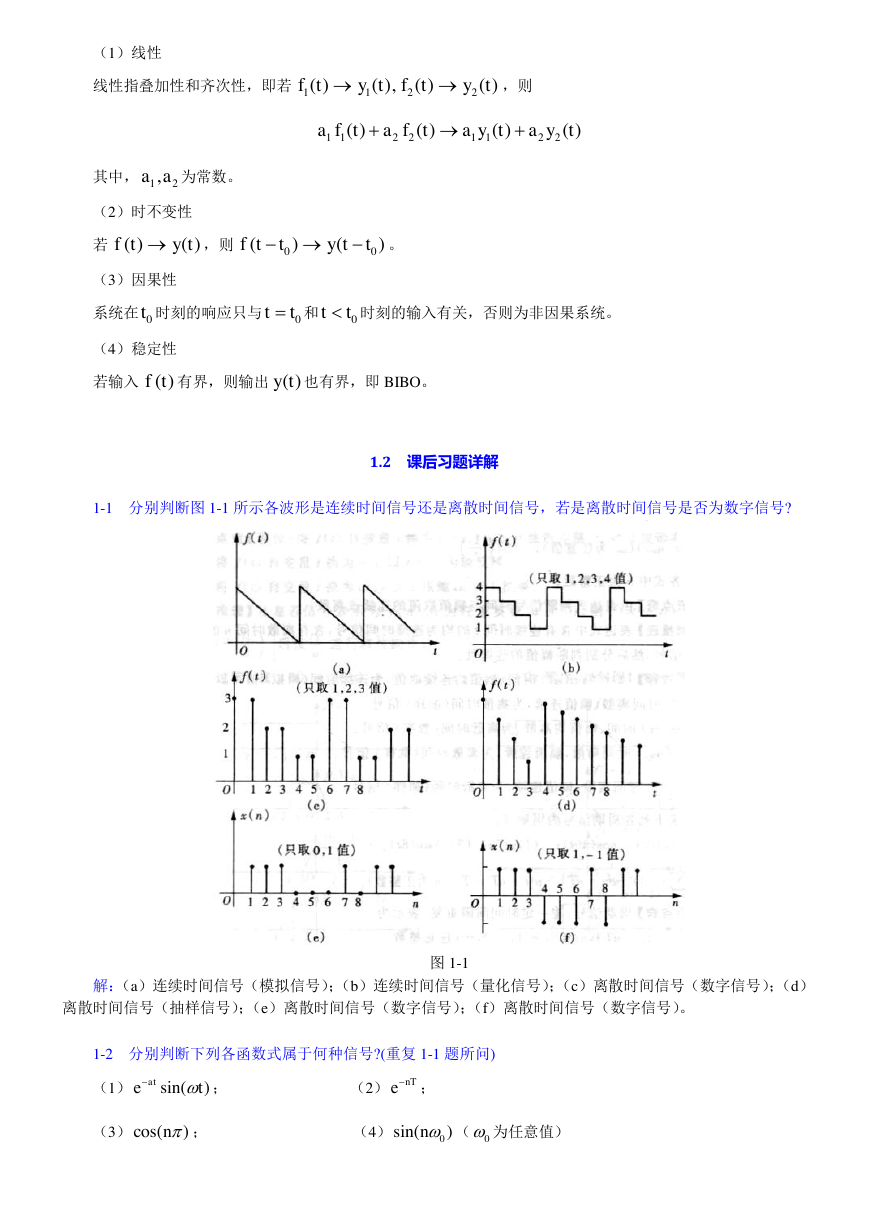
（1）线性线性指叠加性和齐次性，即若，则其中，为常数。（2）时不变性若，则。（3）因果性系统在时刻的响应只与和时刻的输入有关，否则为非因果系统。（4）稳定性若输入有界，则输出也有界，即 BIBO。 1.2 课后习题详解 1-1 分别判断图 1-1 所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号? 解：（a）连续时间信号（模拟信号）；（b）连续时间信号（量化信号）；（c）离散时间信号（数字信号）；（d）离散时间信号（抽样信号）；（e）离散时间信号（数字信号）；（f）离散时间信号（数字信号）。图 1-1 1-2 分别判断下列各函数式属于何种信号?(重复 1-1 题所问) （1）；（2）；（3）；（4）（为任意值） 1122()(),()()ftytftyt11221122()()()()aftaftaytayt12,aa()()ftyt00()()fttytt0t0tt0tt()ft()ytsin()atetnTecos()n0sin()n0

（5）。以上各式中 n 为正整数。解：（1）时间、幅值均连续取值，故为连续时间信号（模拟信号）；（2）时间离散、幅值连续，故为离散时间信号（抽样信号）；（3）时间、幅值均离散，故为离散时间信号（数字信号）；（4）时间离散、幅值连续，故为离散时间信号（抽样信号）；（5）时间离散、幅值连续，故为离散时间信号（抽样信号）。 1-3 分别求下列各周期信号的周期 T：（1）；（2）；（3）；（4）。解：（1）分量的周期，分量的周期，两者的最小公倍数是，所以此信号的周期。（2）因为（3）因为。（4）原式可整理为，所以此信号周期为。，所以此信号的周期为所以此信号的周期为 2T。 1-4 对于教材例 1-1 所示信号，由 f（t）求 f(-3t-2)，但改变运算顺序，先求 f(3t)或先求 f(-t)，讨论所得结果是否与原例结果一致。解法一：图 1-2 1()2nsin()atetnTecos()n0sin()n1()2ntt30cos10costje1028sin5t为正整数nTnTtunTtun|1cos(10)t12105Tcos(30)t215T55T10cos(10)sin(10)jtetjt2105T221cos(16)[5sin(8)]25sin(8)2512.512.5cos(16)2tttt2168T()(3)(3)(32)ftftftft

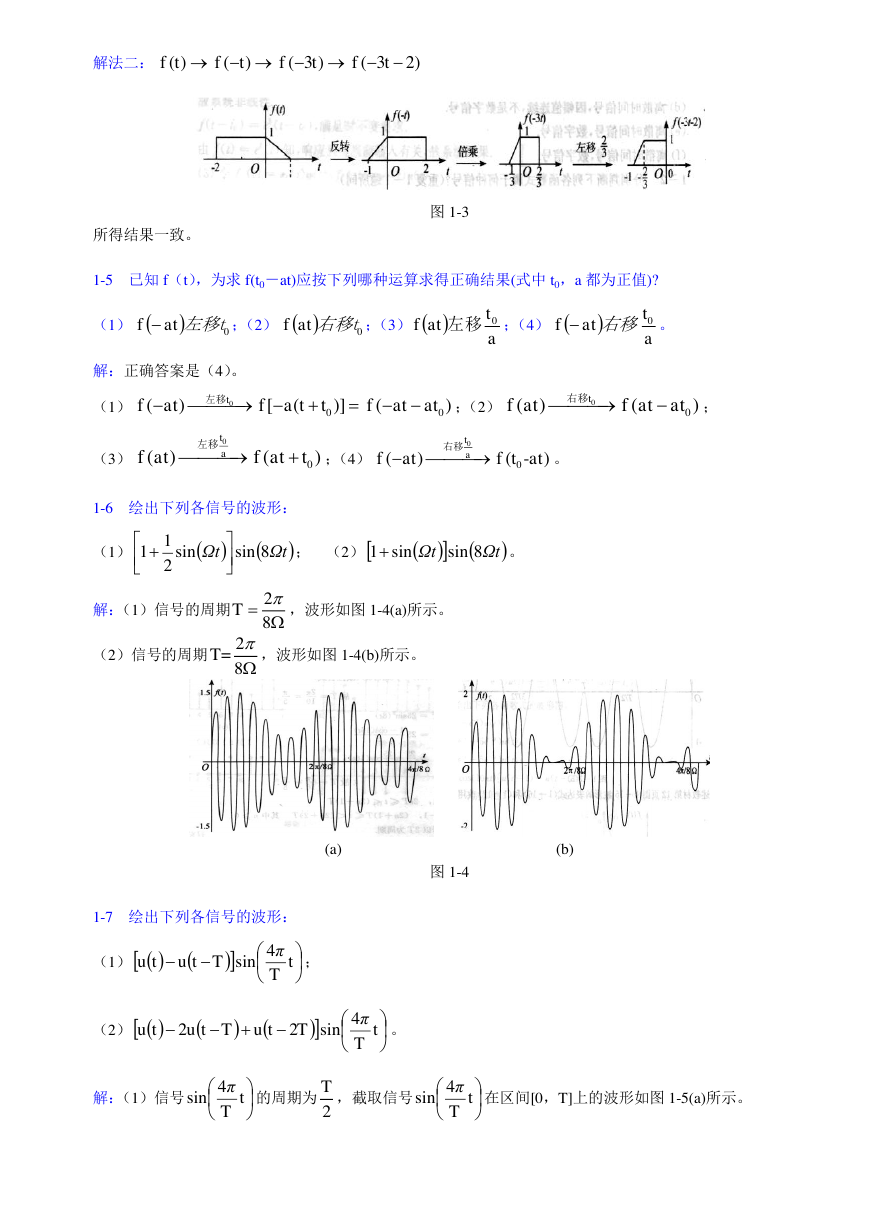
解法二：图 1-3 所得结果一致。 1-5 已知 f（t），为求 f(t0－at)应按下列哪种运算求得正确结果(式中 t0，a 都为正值)? （1）；（2）；（3）；（4）。解：正确答案是（4）。（1）（3） 1-6 绘出下列各信号的波形：；（2）；；（4）。（1）；（2）。解：（1）信号的周期，波形如图 1-4(a)所示。（2）信号的周期，波形如图 1-4(b)所示。 (a) (b) 图 1-4 1-7 绘出下列各信号的波形：（1）（2）；。解：（1）信号的周期为，截取信号在区间[0，T]上的波形如图 1-5(a)所示。 ()()(3)(32)ftftftft0左移tatf0右移tatfaat0tf左移at右移atf0000()[()]()tfatfattfatat左移00()()tfatfatat右移00()()tafatfatt左移00()(-)tafatftat右移ΩtΩt8sinsin211ΩtΩt8sinsin128T2T=8tTπTtutu4sintTπTtuTtutu4sin22tTπ4sinT2tTπ4sin

（2）信号的周期为，截取信号在区间[0，T]上的波形，在区间[T，2T]上将其反相，所得波形如图 1-5(b)所示。 (a) (b) 图 1-5 1-8 试将教材中描述图 1-15 波形的表达式(1-16)和(1-17)改用阶跃信号表示。解：（1）表达式（1-16）为改用阶跃函数可表示为（2）表达式（1-17）为图 1-6 改用阶跃信号可表示为 tTπ4sinT2tTπ4sin0)=atattateftee（（）00(0)()tttt当当0()00()()()attatatfteututteeutt（）00()000()0()()()()()()attatatatattateuteutteutteutteuteutt()0001(1),(0)=11(1)1,()attattatettafeettaa（）d

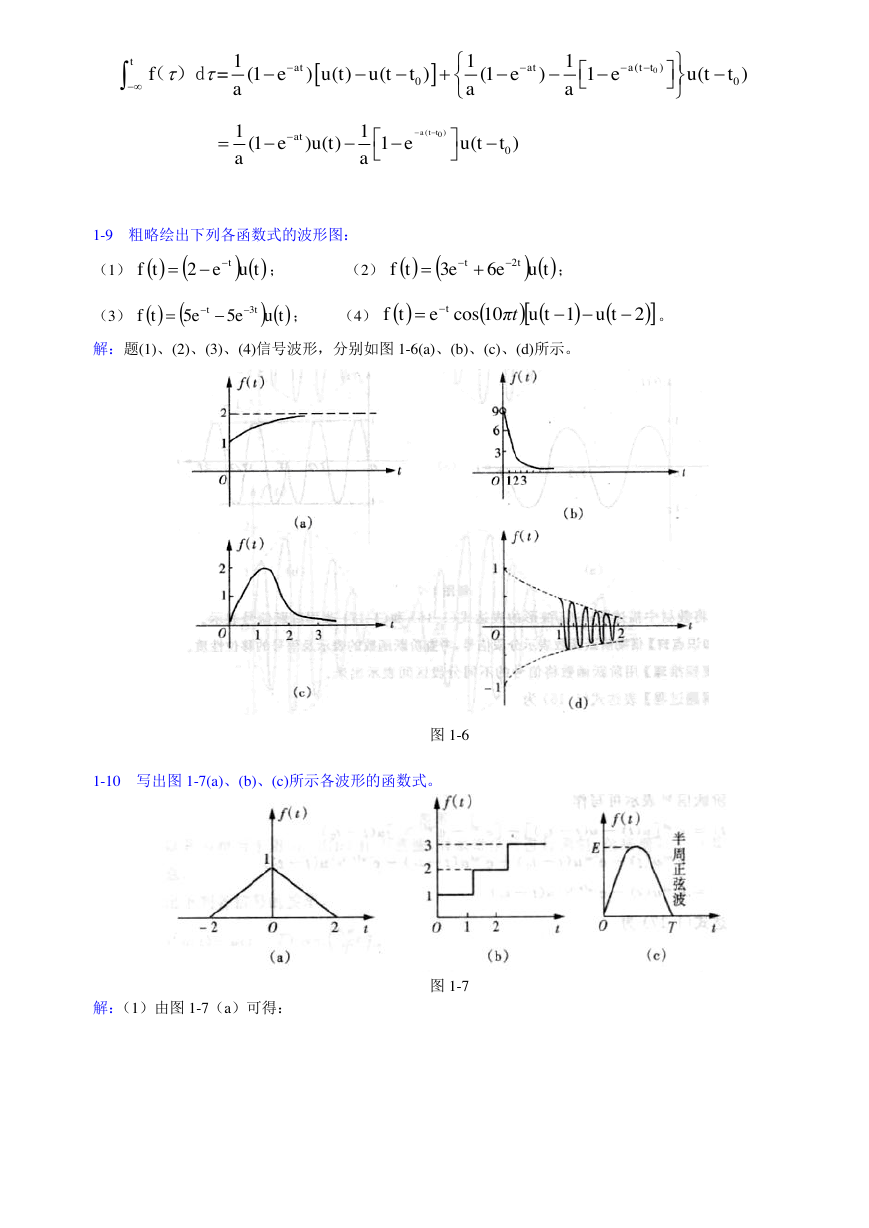
1-9 粗略绘出下列各函数式的波形图：（1）；（2）；（3）；（4）。解：题(1)、(2)、(3)、(4)信号波形，分别如图 1-6(a)、(b)、(c)、(d)所示。 1-10 写出图 1-7(a)、(b)、(c)所示各波形的函数式。图 1-6 解：（1）由图 1-7（a）可得：图 1-7 0()00111=(1)()()(1)1()tattatatfeututteeuttaaa（）d()0011(1)()1()attateuteuttaatuetft2tueetftt263tueetftt3552110costutuπtetft

分享到：

赞收藏

资料库

郑君里《信号与系统》（第3版）笔记和课后习题（含考研真题）详解.pdf

相关推荐

课程资源

热门标签

最新资料