五一建模赛B题.pdf-资料库

m0_51780913-18747305-16359647664314515304.pdf-第1页.png

第1页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第2页.png

第2页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第3页.png

第3页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第4页.png

第4页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第5页.png

第5页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第6页.png

第6页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第7页.png

第7页 / 共22页

m0_51780913-18747305-16359647664314515304.pdf-第8页.png

第8页 / 共22页

五一数学建模竞赛承诺书我们仔细阅读了五一数学建模竞赛的竞赛规则。我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与本队以外的任何人（包括指导教师）研究、讨论与赛题有关的问题。我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其它公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。如有违反竞赛规则的行为，我们愿意承担由此引起的一切后果。我们授权五一数学建模竞赛组委会，可将我们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。参赛题号（从 A/B/C 中选择一项填写）： B

五一数学建模竞赛题目：针对消防救援模型的分析与预测关键词：消防救援，回归分析，预测分析，模型优化摘要：随着我国经济的高速发展，城市空间环境复杂性上升，事故灾害频发，消防救援队承担的任务也呈现多样化、复杂化。通过消防记录，本文使用各种数据分析方法对消防灾害进行分析与预测，并提出相应方案。问题一，针对值班问题，本文将使用统计分析各时间段的灾害趋势，得出集中趋势数据，在满足出警任务需求下完成最小规模人员统筹与安排问题二，针对各月份灾害预测，本文将尝试使用多元线性回归模型，boxTidwell 变换和马尔可夫算法进行分析预测，力求与第五年数据预测的高准确性与高拟合度，从而来预测 2021 年的各数据问题三，针对各事件发生次数与月份之间的相关模型，本文采用多元线性回归模型和多相似回归模型来确定每类时间发生次数的最优模型问题四，针对各类时间密度在空间上的相关性，本文在对数据进行统计分析与处理后，使用皮尔逊相关系数与斯皮尔曼秩相关系数来对区域事件相关性进行分析问题五，分析时间密度与人口密度的关系，本文通过线性回归分析，发现了拟合度极高的线性回归模型来描述时间密度与人口密度之间的关系问题六，针对提供的有权无向图，本文先采用 Floyd 算法来获取每个节点之间的最短路径，然后对每个地区的事件发生概率及逆行统计分析，得出其集中趋势，然后使用 Python 来枚举各个顶点，通过模拟消防救灾与路程花费等因素，并通过 K-means 算法进行检验分析。综合各项结果，最终为消防站新建的选址提供建议与解决方案（前面两页必须使用模板格式，否则论文检测不通过）此页为论文正文开始处

一、问题分析与解答 1.背景知识 2.数据分析本题一共给出了两个附件数据，本文将对这些附件进行初步的解读。附件一：附件一给出了 15 个区域的基本信息，这些信息由两部分组成。第一部分是城市对应的人口数量，第二部分则是各区域的面积。附件二：附件二给出了每个地点的消防出警数据，而这些数据由 4 部分组成。第一部分是出警的日期，第二部分是当天具体的出警时间，第三部分是事故发生的所在城市，第四部分则是发生的事故的所属类型。 3.具体问题根据题意，本文主要解决的问题主要有六个。 1. 如果将每天分为三个时间段（0:00-8:00 为时段Ⅰ，8:00-16:00 为时段Ⅱ，16:00-24:00 为时段Ⅲ），并且每个时间段安排不少于 5 人值班。假设消防队每天有 30 人可安排值班，根据附件 2 中消防救援队出警数据数据，建立数学模型，确定消防队在每年 2 月、5 月、8 月、11 月中第一天的三个时间段各应安排多少人值班。 2. 以该地 2016 年 1 月 1 日至 2019 年 12 月 31 日的数据为基础，以月份为单位，建立消防救援出警次数的预测模型；以 2020 年 1 月 1 日至 2020 年 12 月 31 日的数据作为模型的验证数据集，评价模型的准确性和稳定性，并对 2021 年各月份的消防救援出警次数进行预测，完成表 1。 3. 依据 7 种类别事件的发生时间，建立各类事件发生次数与月份关系的多种数学模型，以拟合度最优为评价标准，确定每类事件发生次数的最优模型。 4. 根据图 1，建立数学模型，分析该地区 2016-2020 年各类事件密度在空间上的相关性，并且给出不同区域相关性最强的事件类别（事件密度指每周每平方公里内的事件发生次数）。 5. 依据附件 2，建立数学模型，分析该地各类事件密度与人口密度之间的关系（人口密度指每平方公里内的人口数量）。 6. 目前该地有两个消防站，分别位于区域 J 和区域 N，依据附件 1 和附件 2，综合考虑各种因素，建立数学模型，确定如果新建 1 个消防站，应该建在哪个区域？如果在 2021-2029 年每隔 3 年新建 1 个消防站，则应依次建在哪些区域？

4.分析与解答 4.1 问题一的分析与求解 4.1.1 问题一的分析思路对于问题一我们可以按照统计分析的思路进行深入思考。首先我们根据每年的 2 月初、五月初、八月初以及 11 月初这四个时间的灾害发生的频次进行统计，并且根据每天的三个不同时间段（ 0:00-8:00 为时段 Ⅰ ， 8:00-16:00 为时段 Ⅱ ， 16:00-24:00 为时段Ⅲ）的发生灾害的次数进行统计，并通过分析，来做出最合理化的值班人员分配安排。我们选取切尾均值的分析方法，进行数据处理与分析。不同于求平均值或者是四分位数的求解方法，切尾均值能够很好有效的规避极端数据情况对于小样本的影响，保证了数据处理结果的相对精确性。同时，切尾均值分析方法能够在人员数量合宜的样本中，表示在实际问题中的最优数量方法。在本问题中，我们需要在保证值班人员完全符合可能出警情况的要求后，尽可能的节省人员使用率，形成资源配置利用率的最大化，从而寻求得问题的最优解。 4.1.2 问题一的数据分析与处理 1）出警数量我们根据灾害发生频次，并通过切尾均值的研究方式，算得每一个时间段的出警数量。从而以出警数量来作为一段时间内所需要的值班人数的最低要求，衡量值班人数的最小基数。 2）值班人数根据有关消防控制室管理及应急程序的管理办法要求，消防控制室必须实行每日 24 小时专人值班制度，每班不应少于 2 人。所以我们在安排值班人数时候，设立了“4+2”的原则，即有一次出警 4 人，固定至少有 2 人在出警时留守值班，进行相关调度等候和协调管理。 4.1.3 对于出警情况变量选取和最优值班人数模型的建立解决本题的关键在于，我们既要寻找到满足各类条件的人数合理解，又要考虑人数资源利用率最大化的最优解。根据题意，做出了对人员数量除保证不超过 30 人外的其他要求的限制，但为了寻得这个最优解，我们建立以下模型。 1）出警次数 (1) 其中，表示出警次数。中，k 表示年份，i 表示月份中的某日，j 表示该日的具体时间段。表示某年某天中某一时间段的具体出警次数。 2020 在（1）式中， =2016 的分析计算是为了反应数据变化的集中趋势，能够相对准确的预估警情发生的情况，是运用了切尾均值的算法进行合理化分析。 = =2016 −min () 2020 − −min () 从而合理的安排值班人数最优解。

2）留守值班人数留守= 守+·,>0 ,=0 W 表示每次出警数量，常=5，表示无出警任务最少的留守人数。常 4.1.4 问题一的求解将附件二中的消防出警数据代入公式（1）（2），得到以下数据（2）根据 4+2 原则，即有一次出警 4 人，固定至少 2 人在出警时留守。如果没有出警则安排最少 6 个人值班的策略从而得出以上分配合理。综上所述，2.1，5.1，8.1，11.1 各时间段应该安排的人数为： 0：00-8：00 8：00-16：00 16：00-24：00 10 10 6 6 10 10 6 6 2.1 5.1 8.1 11.1 6 6 6 6 4.2 问题二的分析与求解 4.2.1 问题二的分析思路问题给出了从 2016 年 1 月 1 号到 2020 年 12 月 31 日该地消防救援队的出警数据，要求我们根据 2016 年到 2019 年的数据建立模型，并以 2020 年的数据作为验证的对象，从而预测出 2021 年各个月的消防出警情况。我们认为本题中，作为应变量的出警情况可以与作为自变量的年份日期用线形形式来刻画，所以我们采用多元线性回归模型来预测 2021 年的出警情况。首先使用多元线性回归模型得到线性回归结果，再分别对回归结果用 QQ 图和异常值的离群值检

验来检验结果是否结果是否满足正态性，是否具有离群点。对于变量，我们对因变量做线性假设来观察其是否需要非线性转化。同时，我们要会检验变量的独立性和多重共线性。最终，用 2020 年的数据来检测该模型的准确程度。在保证了 80％左右的数据落在 90％的置信区间内，我们便用该模型对 2021 年的数据进行预测并得到结果。 4.2.2 问题二的模型的建立 1）多元线性回归模型多元线性回归模型通常用来研究一个应变量依赖多个自变量的变化关系，如果二者的关系可以用线性形式表示，则可以建立多元线性模型来进行分析。我们这里不妨假设应变量为 y,自变量为 x。则 x 与 y 之间的随机线性关系可以如下表示。 y   0   1 x 1  . . .   k x k   式中， 1 , x x 2 ,..., x 是非随机的变量；y 是随机的应变量； 0 k 如果用矩阵表示，则表示如下。 x 11 x 12 ... x 1 n y= 1 1   1   ...  1  y y 2 ... y ， x =             n ... ... ... 1 x k x 2 k ... x kn       , k 1 , ,...,    是回归系数；ξ是随机误差项。 β=  ，    1    2  ...    n         1    2  ...    n       这时模型可以写作： y  X    得到回归模型参数的估计值后，需要对回归方程和回归系数进行显著性检。 4.2.3 问题二数据的处理及求解结果 1）统计 2016-2019 年每一个月的出警次数，得出四组数据： 1 月 2 月 3 月 4 月 5 月 6 月 7 月 8 月 9 月 10 月 11 月 12 月 2016 2017 2018 2019 79 58 54 67 95 28 129 76 98 44 68 73 51 14 71 44 275 148 107 138 67 87 119 146 63 23 59 72 40 42 50 30 50 49 46 41 31 33 44 26 38 65 40 25 43 68 63 36 2）建立多元线性回归模型自变量为年份和月份，出警次数是我们做的预测。下面是步骤：

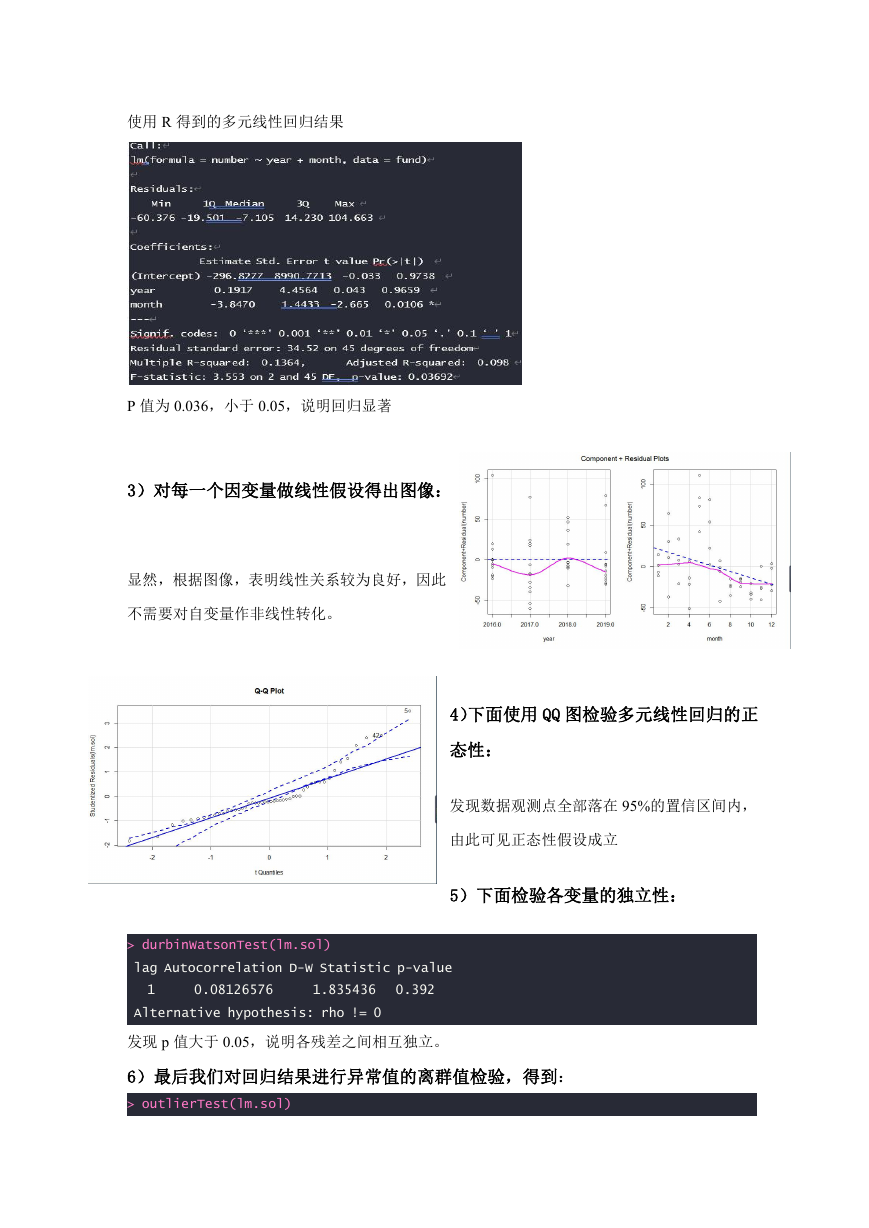
使用 R 得到的多元线性回归结果 P 值为 0.036，小于 0.05，说明回归显著 3）对每一个因变量做线性假设得出图像：显然，根据图像，表明线性关系较为良好，因此不需要对自变量作非线性转化。 4）下面使用 QQ 图检验多元线性回归的正态性：发现数据观测点全部落在 95%的置信区间内，由此可见正态性假设成立 5）下面检验各变量的独立性： > durbinWatsonTest(lm.sol) lag Autocorrelation D-W Statistic p-value 1 0.08126576 1.835436 0.392 Alternative hypothesis: rho != 0 发现 p 值大于 0.05，说明各残差之间相互独立。 6）最后我们对回归结果进行异常值的离群值检验，得到： > outlierTest(lm.sol)

No Studentized residuals with Bonferroni p < 0.05 Largest |rstudent|: rstudent unadjusted p-value Bonferroni p 5 3.500834 我们得到了标准化残差值，其中，P 值大于 0.05， 0.001076 0.051647 因此没有离群点。 8）我们对回归数据进行 boxTidwell 变换并拟合广义泊松曲线。[2] 通过 R 提供的 boxTidwell() 函数通过获得预测变量幂数的最大似然估计来改善线性关系。最终发现对于 R 方的影响不大，因此无需做非线性转换。因此我们得到的多元线性回归方程为： number(出警次数)=0.1917*year-3.8470*month-296.8277 9）由 2020 年的数据得出模型准确率 2020 28 23 28 46 62 55 25 29 36 25 51 62 我们根据得到的线性回归方程进行计算得到 2020 年的数据描述区间对比计算得出的数据区间与实际数据，发现十二个观测点中有 7 个观测点落在了 95% 的置信区间内，有 9 个数据落在了 90%的置信区间，因此模型的准确率在 58%至 75% 之间

资料库

五一建模赛B题.pdf

相关推荐

行业

热门标签

最新资料