SAR image formation toolbox for MATLAB.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书资料大小：0.99M 资料格式：pdf 举报版权申诉

c_1024-15867869-16359647368617622774.pdf-第1页.png

第1页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第2页.png

第2页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第3页.png

第3页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第4页.png

第4页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第5页.png

第5页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第6页.png

第6页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第7页.png

第7页 / 共13页

c_1024-15867869-16359647368617622774.pdf-第8页.png

第8页 / 共13页

文本预览

Algorithms for Synthetic Aperture Radar Imagery XVII, edited by Edmund G. Zelnio, Frederick D. Garber, Proc. of SPIE Vol. 7699, 769906 · © 2010 SPIE · CCC code: 0277-786X/10/$18 · doi: 10.1117/12.855375 Proc. of SPIE Vol. 7699 769906-1 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms SARimageformationtoolboxforMATLABLeRoyA.GorhamandLindaJ.MooreAirForceResearchLaboratory,SensorsDirectorate2241AvionicsCircle,Bldg620,WPAFB,OH45433-7321ABSTRACTWhilemanysyntheticapertureradar(SAR)imageformationtechniquesexist,twoofthemostintuitivemethodsforimplementationbySARnovicesarethematchedﬁlterandbackprojectionalgorithms.Thematchedﬁlterand(non-optimized)backprojectionalgorithmsareundeniablycomputationallycomplex.However,thebackprojec-tionalgorithmmaybesuccessfullyemployedformanySARresearchendeavorsnotinvolvingconsiderablylargedatasetsandnotrequiringtime-criticalimageformation.ExecutionofbothimagereconstructionalgorithmsinMATLABisexplicitlyaddressed.Inparticular,amanipulationofthebackprojectionimagingequationsissuppliedtoshowhowcommonMATLABfunctions,ifftandinterp1,maybeusedforstraight-forwardSARimageformation.Inaddition,limitsforscenesizeandpixelspacingarederivedtoaidintheselectionofanappropriateimaginggridtoavoidaliasing.ExampleSARimagesgeneratedthoughuseofthebackprojectionalgorithmareprovidedgivenfourpubliclyavailableSARdatasets.Finally,MATLABcodeforSARimagereconstructionusingthematchedﬁlterandbackprojectionalgorithmsisprovided.Keywords:SAR,imageformation,matchedﬁlter,backprojectionalgorithm1.INTRODUCTIONOverthepastfourdecades,numerousimageformationalgorithmshavebeendevelopedwithvaryinglevelsofcomplexityandaccuracy.However,thesealgorithmshaveasteeplearningcurveforSARnovices.Inthispaper,weintroducetwoalgorithms-matchedﬁlterandbackprojection-implementedinMATLAB,whichareverysimpletounderstand.Abeneﬁtofmatchedﬁlterimagereconstructionisthatthemethodoﬀersoptimizationofthesignal-to-noiseratio(SNR).1Useofthematchedﬁlterrequiresahypothesisregardingatarget’scharacteristics;theseassumptionsyieldaspeciﬁcallydesignedﬁlterthatwillideallymatchtothetarget.Whilethematchedﬁlteralgorithmisintuitiveandstraight-forward,thegenerationofa2DSARimageusingthistechniquerequiresO(N4)operations.Formostpracticalsituations,thecomputationalcomplexityofthematchedﬁlteralgorithmrendersuseofthemethodunrealistic.However,understandingofthisfundamentalimagingalgorithmisextremelybeneﬁcial,especiallyfortheSARnovice.WhileseveraltechniquesexistforSARimagegeneration,twocommonlyemployedapproachesworthnotingherearethepolarformatandbackprojectionalgorithms.Thesealgorithmsdiﬀerinregardstothetradeoﬀbetweencomputationalcomplexityandimagequality.2,3Thepolarformatalgorithm4,5forSARimagerecon-structionissimilartocomputer-aidedtomographyimagingtechniques.6,7,8Polarformatreconstructionemploysadirect2DFouriertransform,whichprovidestheopportunitytotakeadvantageoftheextremelyeﬃcientfastFouriertransform.PolarformatimagereconstructionrequiresO(N2logN)operationsgivenanNxNSARim-age.Whilemorecomputationallyeﬀectivethanthebackprojectionalgorithm,thepolarformatimagingmethodinvolvesanapproximationofthereceivedsignalphase.Thisapproximationintroduceserrorsintotheﬁnalre-constructedSARimage.SeveralcorrectiontechniqueshavebeensuggestedasameansofimprovingtheaccuracyofSARimagesgeneratedviapolarformatreconstruction.9,10Anotherfrequentlyusedimageformationtechniqueisthebackprojectionalgorithm.7,11AdistinctadvantageofthebackprojectionalgorithmistheabilitytoformSARimagesasphasehistoryiscollected,pulsebypulse,andtointegratenewlyobtainedinformationintotheSARimageasitbecomesavailable.Thebackprojectionalgorithmiscomputationallyexpensive,however,asitrequiresO(N3)operationsforanNxNSARimage.For-tunately,thebackprojectionalgorithmlendsitselfnaturallytoparallelprocessing.BackprojectionhasrecentlyFurtherauthorinformation:(E-mail:leroy.gorham@wpafb.af.milandlinda.moore2@wpafb.af.mil)

Proc. of SPIE Vol. 7699 769906-2 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms beenimplementedongraphicsprocessingunits(GPUs),12,13whichprovideinexpensiveplatformsforparallelcomputing.Severalmethodshavebeenproposedasameansofreducingthecomputationalcomplexityofthebackpro-jectionalgorithmwhileretainingtheadvantagesofthisimageformationapproach.14,15,16,17Manyofthesefastbackprojectionalgorithmsareﬂexible,providingmannersinwhichimagequalitymaybeacceptablysacriﬁcedinordertofurtherimprovedataprocessingtime.Theseimageformationalgorithms,severalofwhicharefavorablegivenwidebandwidthsandlargesyntheticapertures,oﬀerdecreasedcomputationalcomplexitiesofO(N5/2)14andO(N2logN).15,16,17Non-optimizedbackprojectionimagingmaybeimpracticalforexceptionallylargedatasetswithtime-criticalimageformationrequirements;however,knowledgeofthissimpleSARimagingtechniqueisundoubtedlyvaluableformanyresearchendeavors.Theremainderofthispaperisoutlinedasfollows.InSection2,wedeﬁneourterminologyandtheSARsignalmodel.Wealsoderivelimitsforscenesizeandpixelspacingtoaidinselectinganimaginggridthatavoidsaliasing.InSection3,wederiveanddescribethematchedﬁlteralgorithmforimageformation.InSection4,wederiveabackprojectionalgorithm,whichisbasedonthematchedﬁlteralgorithm.WedescribehowtoutilizebasicMATLABfunctionslikeifftandinterp1toimplementthealgorithm.InSection5,weapplythebackprojectionalgorithmtofourpubliclyavailableSARdatasets.Finally,MATLABcodeforthetwoimagingalgorithms,matchedﬁlterandbackprojection,aresuppliedinAppendixA.1andA.2.TheauthorswillbegladtoprovidecopiesoftheMATLABcodeusedtogeneratetheﬁguresprovidedinthispaperinresponsetorequestsviaemail.2.SIGNALMODELThefollowingSARsignalmodel18isusedforthedevelopmentofMATLABimplementationsofthematchedﬁlterandbackprojectionimagingalgorithms.TheSARsensortravelsalongaﬂightpathsuchthattheantennaphasecenterhasathree-dimensionalspatiallocationdenotedra(τ)suchthatra(τ)=[xa(τ),ya(τ),za(τ)]T(1)whereτdenotesthesyntheticaperture,orslowtime,domain.Allcoordinatesaredeﬁnedwithrespecttoasceneorigin,whichcorrespondstotheSARmotioncompensationpoint.Thedistancefromtheantennaphasecentertotheorigin,ra(τ),isdenotedbyda(τ)=x2a(τ)+y2a(τ)+z2a(τ).(2)Atargetisspeciﬁedatalocationr(τ)=[x(τ),y(τ),z(τ)]T.(3)Ingeneral,thistargetcanhaveanyarbitrarymotion,butinthispaper,wewillassumethatthetargetisstationary.Thus,thedependenceonτisdroppedfortheremainderofthederivation.Thetargethasaradarcrosssectionwhichisdependentonfrequencyandaspectangle.Thedistancefromtheantennaphasecentertothetargetisdenotedbyda0(τ)=(xa(τ)−x)2+(ya(τ)−y)2+(za(τ)−z)2.(4)Atperiodicintervals,theradartransmitsapulsethatreﬂectsoﬀscatterersinthescene.Someoftheenergyisthenreceivedbytheradar.Inagivensyntheticaperture,thereareNppulsesusedtoformtheimage.Thetransmissiontimeofeachpulseisdenotedbythesequence{τn|n=1,2,...,Np}.Theoutputofthereceiveratagiventime,τn,isasequenceofband-limitedfrequencysamplesdelayedwithrespecttothetimeofpulsetransmissionbytheround-triptimetothetarget.ThereareKfrequencysamplesperpulse,andtheassociatedfrequencyvaluesarerepresentedbythesequence{fk|k=1,2,...,K}.ThereceiveroutputfromthetargetlocatedatrisS(fk,τn)=A(fk,τn)exp−j4πfkΔR(τn)c.(5)

Proc. of SPIE Vol. 7699 769906-3 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms Theamplitude,A(fk,τn),isrelatedtotheradarcrosssectionofthetargetwhilethephaseisdependentonthefrequencyofeachsampleandonthediﬀerentialrange,ΔR(τn),givenbyΔR(τn)=da0(τn)−da(τn).(6)Equation(5)assumesthateachpulseismotioncompensatedsuchthatascattereratthesceneoriginwillhavezerophaseforallfkandτn.Theactualreceiveroutputisthusthesumofthecontributionsofallscatterersinthescene.Thefrequencysamples,{fk},haveaminimumvaluedenotedbyf1,amedianvaluedenotedbyfc,amaximumvaluedenotedbyfK,andastepsizedenotedbyΔf.Thefrequencystepsizeisinverselyrelatedtothemaximumalias-freerangeextentoftheimage,Wr,byWr=c2Δf.(7)Thus,thefrequencystepsizeischosentomatchthesizeofthescenetobeimaged.Thetotalbandwidth,B,ofthereceivedpulseisB=(K−1)Δf.Therangeresolutionisthusδr=c2B=c2(K−1)Δf.(8)Inasimilarmannerasabove,theazimuthangletraversedduringthesyntheticaperturedeterminesthecross-rangeresolution,andtheazimuthanglefrompulsetopulsedeterminesthemaximumalias-freecross-rangeextentoftheimage,Wx.GivenanazimuthstepsizeofΔθ,Wx=λmin2Δθ(9)whereλministheminimumwavelengthsuchthatλmin=c/fK.Thetotalazimuthangle,θa,traversedduringthesyntheticapertureisθa=(Np−1)Δθ.Thus,thecross-rangeresolution,δx,isgivenbyδx=λc2θa=λc2(Np−1)Δθ(10)whereλcisthecenterwavelengthsuchthatλc=c/fc.Toutilizetheimagingalgorithmsdescribedinthispaper,onecanselectanyarbitrarypixellocations.How-ever,oneshouldbecarefulwhenselectingtheselocationstoavoidaliasingoftheimageorthefrequencysupport.ThepixelspacingshouldbeﬁnerthantheresolutiondeﬁnedinEquations(8)and(10)andtheoverallscenesizeshouldbelessthanthemaximumscenesizedeﬁnedinEquations(7)and(9).3.MATCHEDFILTERALGORITHMThemoststraightforwardmethodforformingaSARimageistoperformamatchedﬁlter.Onecanbuildthematchedﬁltertoanykindofscatterer,butherewewillassumeanisotropicpointscatterer.ThereceivedsignalfromapointscattereratlocationrisgiveninEquation(5).AnisotropicscattererwillhaveaconstantamplitudeandthusA(fk,τn)=A0.Therefore,thematchedﬁlterresponse,denotedbyI(r),atlocationrisgivenbyI(r)=1NpKNpn=1Kk=1S(fk,τn)exp+j4πfkΔR(τn)c=A0,(11)assumingasinglescattererinthescene.Toformanimageusingthismethod,Equation(11)isappliedforeachpixelintheimage.Thisrequirescalculationofthediﬀerentialrange,ΔR(τn),foreverypixelforeverypulse.ThealgorithmhasacomputationalcomplexityofO(N4)for2Dimages,whichmakesitimpracticalformostapplications.However,Equation(11)formsthebasisforthederivationofthebackprojectionalgorithminSection4.MATLABcodeforthematchedﬁlteralgorithmisprovidedinAppendixA.1.

Proc. of SPIE Vol. 7699 769906-4 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms MATLABTypeSymbolDescriptionUnitsdata.deltaFscalarΔfFrequencystepsizeHzdata.minFNpvectorf1MinimumfrequencyforeverypulseHzdata.NfftscalarNfftLengthofFFT(backprojectiononly)data.xmatArbitraryrXcoordinateofeverypixelintheimagemdata.ymatArbitraryrYcoordinateofeverypixelintheimagemdata.zmatArbitraryrZcoordinateofeverypixelintheimagemdata.AntXNpvectorraAntennalocationforeverypulsemdata.AntYNpvectorraAntennalocationforeverypulsemdata.AntZNpvectorraAntennalocationforeverypulsemdata.R0Npvectorda(τn)Distancetothemo-comppointmdata.phdata(KxNp)arrayS(fk,τn)Complexphasehistorydata,Eq.(5)Table1.NecessaryﬁeldsintheMATLABdatastructureforimageformation.x (m)y (m)−5−4−3−2−1012345−5−4−3−2−1012345−50−45−40−35−30−25−20−15−10−50(a)matchedﬁlterimagex (m)y (m)−5−4−3−2−1012345−5−4−3−2−1012345−50−45−40−35−30−25−20−15−10−50(b)backprojectionimageFigure1.ComparisonofSARimages(indB)of3pointtargets,locatedat(0,0,0),(-3,2,0),and(1,4,0),generatedusingthe(a)matchedﬁlterand(b)backprojectionalgorithms.InordertousetheMATLABfunction,mfBasic,theinputsareprovidedinastructurecalleddata.TheﬁeldsofthisstructurearedeﬁnedinTable1.Theimagepixellocations,r,arespeciﬁedinthepixellocationmatricesdata.xmat,data.ymatanddata.zmatwhichcontainthe(x,y,z)locationsofeachpixel.Theoutputimageisstoredindata.imfinal,whichhasthesamedimensionsasthepixellocationmatrices.Whilethesepixelscanhavearbitrarypositions,itisoftendesirabletoformanimageontoaregular2Dor3Dgrid.Inthiscase,theMATLABfunctionmeshgridisusefultobuildthepixellocationmatrices.Inalltheimageexamplesprovidedinthispaper,meshgridwasusedtobuilddata.xmatanddata.ymat,whiledata.zmatwasﬁlledwithzeros.IfaDigitalElevationMap(DEM)isavailable,data.zmatcanbeﬁlledwithinterpolatedheightvaluesforeverypixeltoimproveimagequality.Figure1(a)showsanexampleofanimageformedusingthematchedﬁlteralgorithm.Phasehistorydatawassimulatedfor3pointtargetsusingEquation(5)whereA(fk,τn)=1.Here,Np=128pulsesweresimulatedwithK=512frequencysamplesperpulse,acenterfrequencyof10GHzanda600MHzbandwidth.Acircularﬂightpathwasusedwitha30degreedepressionangleandaslantrangeof10km.A3degreeintegrationanglewasusedwithacenterazimuthangleof50degrees.Thesceneextentwas10mx10mwith2cmpixelspacingineachdimension.

Proc. of SPIE Vol. 7699 769906-5 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms 4.BACKPROJECTIONALGORITHMThebackprojectionalgorithmoﬀersanintuitiveimagingtechniqueforSARnovices.Whilethebackprojectionalgorithmiscomputationallyexpensive,itsimplementationisnotunreasonableformanySARresearchventures.Inthissection,backprojectionimagingequationsaremanipulatedinordertoillustratehowthealgorithmcanbeexecutedthroughuseofcommonMATLABfunctions.4.1DerivationofEﬃcientCalculationofRangeProﬁlesThematchedﬁlterresponseshowninEquation(11)canbeusedtocomputethetargetresponseatadiscreterangebin,m.GivenSARphasehistory,S(fk,τn),collectedbyNppulsesoverarangeofKfrequencies,therangeproﬁleatrangebinmgivenareceivedpulseatslowtimeτniss(m,τn)=Kk=1S(fk,τn)exp+j4πfkΔR(m,τn)c.(12)Bysubstitutingthefrequencyvaluesfk=(k−1)Δf+f1intoEquation(12),therangeproﬁlemayberewrittenass(m,τn)=Kk=1S(fk,τn)exp+j4π((k−1)Δf+f1)ΔR(m,τn)c=Kk=1S(fk,τn)exp+j4πΔfΔR(m,τn)(k−1)c++j4πf1ΔR(m,τn)c=Kk=1S(fk,τn)exp[Φ(ΔR(m,τn))·(k−1)]exp+j4πf1ΔR(m,τn)c(13)wherephasefunctionΦ(ΔR(m,τn))=(+j4πΔfΔR(m,τn))/c.InordertoimplementthebackprojectionalgorithminMATLAB,Equation(13)mustberewrittenintermsofMATLAB’sinversediscreteFouriertransform(ifft)function.InMATLAB,thedeﬁnitionsofthediscreteFouriertransformsbetweenX(k)andx(m)aregivenas19X(k)=Mm=1x(m)·ω(m−1)(k−1)Kx(m)=1KKk=1X(k)·ω−(m−1)(k−1)K(14)whereωK=exp(−j2π/K).Therefore,theinversediscreteFouriertransformofX(k)isgivenasx(m)=ifft(X(k))=1KKk=1X(k)exp+j2π(m−1)K·(k−1)=1KKk=1X(k)exp(Θ(m)·(k−1))(15)whereΘ(m)=(j2π(m−1))/K.InordertowriteEquation(13)intermsofMATLAB’sifftfunction,thepreviouslydeﬁnedphasefunction,Φ(ΔR(m,τn)),fromEquation(13),mustequalΘ(m)fromEquation(15).Tosatisfythisrequirement,thefollowingequalitymusthold:ΔR(m,τn)=(m−1)K·c2Δf=(m−1)K·Wr.(16)NotethatΔR(m,τn)representsasamplingacrossrangeandthemaximumunambiguousrangeoccurswhen(m−1)=K(recallEquation(7)).

Proc. of SPIE Vol. 7699 769906-6 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms InsertingtheresultfromEquation(16)intoEquation(13)yieldss(m,τn)=Kk=1S(fk,τn)exp+j4πΔf(k−1)c·ΔR(m,τn)·exp+j4πf1ΔR(m,τn)c=Kk=1S(fk,τn)exp+j4πΔf(k−1)c·m−1K·c2Δf·exp+j4πf1ΔR(m,τn)c=Kk=1S(fk,τn)exp+j2π(m−1)K·(k−1)·exp+j4πf1ΔR(m,τn)c.(17)Finally,recallingtheexpressionfortheinversediscreteFouriertransformfromEquation(15),therangeproﬁlemaybeexpressedintermsofMATLAB’sifft.s(m,τn)=K·ifft(S(fk,τn))·exp+j4πf1ΔR(m,τn)c(18)TheconstantKappearsinEquation(18)becausebydeﬁnition,theinversediscreteFouriertransformcon-tainsascalingfactorof1/K.Inaddition,it’simportanttonotethattheMATLABimplementationoftheinversediscreteFouriertransformassumesthatKiseven.However,forvaluesofKthatarepowersof2,thecomputationalcomplexityoftheinversediscreteFouriertransformisoptimized.ByinsertingtheexpressionforΔR(m,τn)fromEquation(16),analternativeexpressionfortheimplementationofarangeproﬁleinMATLABisgivenbys(m,τn)=K·ifft(S(fk,τn))·expj2πf1(m−1)KΔf.(19)Oneﬁnalconsiderationmustbeaddressed.Eachpulseismotioncompensatedsuchthatascattereratthesceneoriginhaszerophaseandwillappearinthezerofrequencybinintherangeproﬁle.ThisbincorrespondstothecenteroftherangeproﬁlecomputedinEquation(19).Bydefault,thefunctionifftcomputesthevaluesfrom1≤m≤Kwherem=1correspondstothezerofrequencybin.Toputm=1atthecenteroftherangeproﬁle,thecommandfftshiftisappliedtotheoutputoftheifftcommand.ThisoperationensuresthattheoutputiscorrectlyorderedfollowingtheinversediscreteFouriertransformoperationandthatthezerofrequencycomponentcorrespondstothecenteroftheoutputvector.Asaresult,rangeindex,m,acquiresvaluesbetween−K/2+1andK/2.Therefore,ΔR(m,τn)ofEquation(16)hasvaluesbetween−Wr/2andWr/2−Wr/KandEquation(19)becomess(m,τn)=K·fftshift{ifft(S(fk,τn))}·expj2πf1(m−1)KΔf.(20)4.2ImageFormationProcessForimplementationofthebackprojectionimagingalgorithminMATLAB,Equation(6)isusedtocomputethediﬀerentialrange,ΔR(τn),foreachpixel,foreachpulse,wherethepixel(x,y,z)coordinatesareinsertedintoEquation(4).InordertouseEquation(20)toformaSARimage,aninterpolationstepisrequiredduetothefactthatthediscretevaluesofΔR(m,τn)donotcorrespondexactlytotheΔR(τn)valuescalculatedforeverypixel.Thereareseveralmethodsforperformingthisinterpolation,20,11butherewewillsimplyusetheMATLABinterp1functiontoimplementlinearinterpolation.Sinces(m,τn)isaband-limitedsignal,theidealinterpolatorisasincinterpolator.Thiscanbeapproximatedbyzero-paddingtheifftcomputationandthenperforminglinearinterpolationontheinversediscreteFouriertransformoutput.Agoodruleofthumbisthatthelengthoftheifft,denotedNfft,shouldbe10timesthelengthofthedata,K.Also,theifftfunctionismosteﬃcientwhenNfftisapowerof2.Inthebackprojectionalgorithm,Nfftisprovidedasaninputtotheimagingfunction,asshowninTable1.

Proc. of SPIE Vol. 7699 769906-7 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms TheﬁrststepintheimageformationprocessistoimplementEquation(20)foreverypulse,zero-paddingthedatasuchthatthelengthoftheifftisNfft.Thus,s(m,τn)=Nfft·fftshift{ifft(S(fk,τn))}·expj2πf1(m−1)NfftΔf.(21)whereS(fk,τn)=0forallk>K.Toﬁndtheimageresponseforapixelatlocationr,givenpulsen,ΔR(τn)iscalculatedandusedtoﬁndaninterpolatedvalueofs(m,τn).Thisisdenotedassint(r,τn).Theﬁnalimageresponse,I(r),issimplythesummationofthesevaluesforeverypulse.I(r)=Npn=1sint(r,τn).(22)Figure1(b)showsanexampleofanimageformedusingthebackprojectionalgorithm.TheimagewasgeneratedusingthesamedataandequivalentpixellocationsasthoseemployedinFigure1(a).5.IMAGEEXAMPLESInthelastfewyears,theAirForceResearchLaboratory(AFRL)hasreleasedseveraldatasetsofbothsyntheticandmeasuredSARdata.Inthissection,thebackprojectionalgorithmintroducedinSection4isappliedtodatafromtheBackhoeDataDome,the2D/3DVolumetricChallengeProblem,andtheSAR-basedGroundMovingTargetIndicator(GMTI)ChallengeProblem.Inaddition,theimagingcodewasimplementedontheCivilianVehicleRadarDataDomessyntheticdatasetfromTheOhioStateUniversity.5.1BackhoeDataDomeIn2004,AFRLreleasedasyntheticallygenerateddatadomeofabackhoetarget.21Thescatteredﬁelddataforthebackhoewascomputedona2π-steradiandatadomeoverthetargetforafrequencybandwidthof5.9GHzatacenterfrequencyof10GHz.x (m)y (m)−5−4−3−2−1012345−5−4−3−2−1012345−70−60−50−40−30−20−100Figure2.Backprojectionimage(indB)usingtheBackhoeDataDomesyntheticdataset.ThebackprojectionalgorithmwasperformedonthisdatasetandaresultingimageisgiveninFigure2.Thedataimagedconsistedofall360◦aspectanglesfromasingleelevationof10◦usingVVpolarization.Thefull5.9GHzbandwidthwasusedtoformtheimage.Thesceneextentis10mx10mwith2cmpixelspacing,resultingina501x501pixelimage.Nowindowingwasappliedtothedatabeforeimaging.ThecalculatedmaximumscenesizeisWr=12.97m;Wx=9.27m.

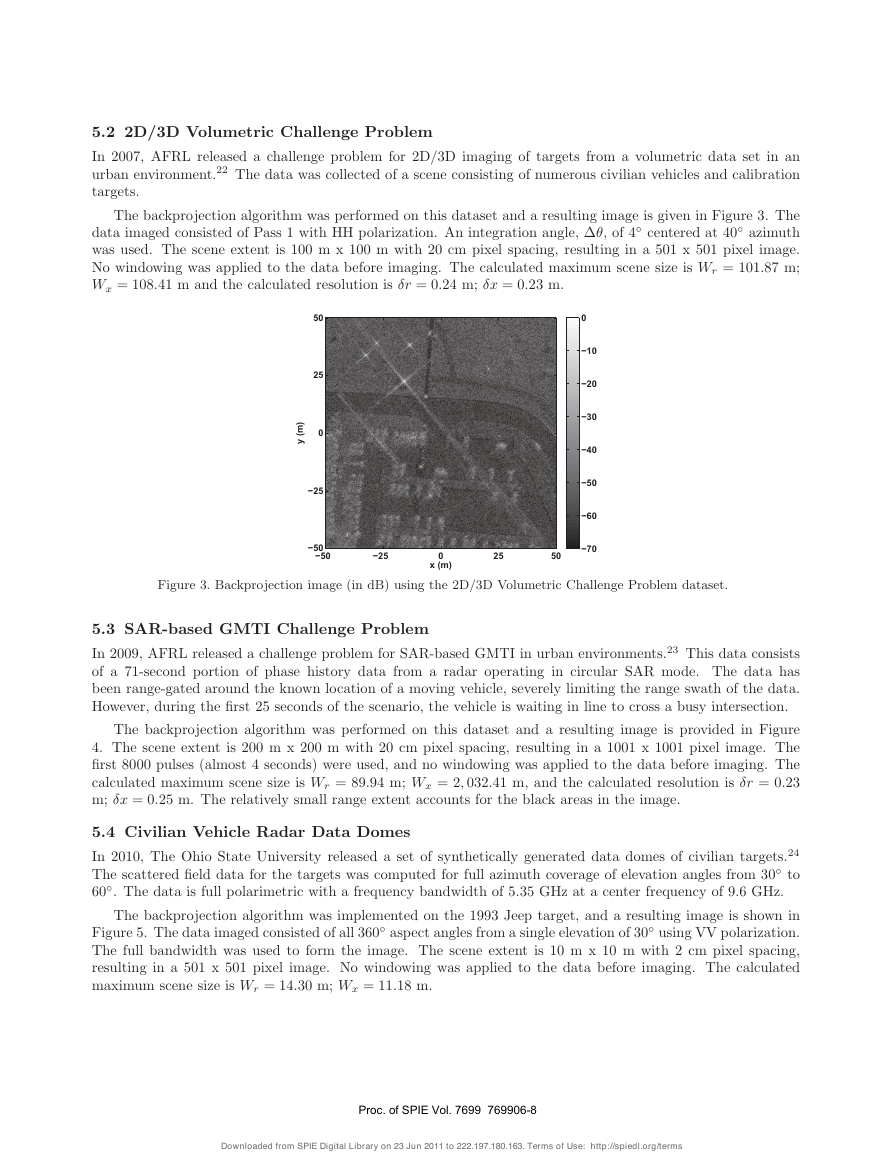
Proc. of SPIE Vol. 7699 769906-8 Downloaded from SPIE Digital Library on 23 Jun 2011 to 222.197.180.163. Terms of Use: http://spiedl.org/terms 5.22D/3DVolumetricChallengeProblemIn2007,AFRLreleasedachallengeproblemfor2D/3Dimagingoftargetsfromavolumetricdatasetinanurbanenvironment.22Thedatawascollectedofasceneconsistingofnumerouscivilianvehiclesandcalibrationtargets.ThebackprojectionalgorithmwasperformedonthisdatasetandaresultingimageisgiveninFigure3.ThedataimagedconsistedofPass1withHHpolarization.Anintegrationangle,Δθ,of4◦centeredat40◦azimuthwasused.Thesceneextentis100mx100mwith20cmpixelspacing,resultingina501x501pixelimage.Nowindowingwasappliedtothedatabeforeimaging.ThecalculatedmaximumscenesizeisWr=101.87m;Wx=108.41mandthecalculatedresolutionisδr=0.24m;δx=0.23m.x (m)y (m)−50−2502550−50−2502550−70−60−50−40−30−20−100Figure3.Backprojectionimage(indB)usingthe2D/3DVolumetricChallengeProblemdataset.5.3SAR-basedGMTIChallengeProblemIn2009,AFRLreleasedachallengeproblemforSAR-basedGMTIinurbanenvironments.23Thisdataconsistsofa71-secondportionofphasehistorydatafromaradaroperatingincircularSARmode.Thedatahasbeenrange-gatedaroundtheknownlocationofamovingvehicle,severelylimitingtherangeswathofthedata.However,duringtheﬁrst25secondsofthescenario,thevehicleiswaitinginlinetocrossabusyintersection.ThebackprojectionalgorithmwasperformedonthisdatasetandaresultingimageisprovidedinFigure4.Thesceneextentis200mx200mwith20cmpixelspacing,resultingina1001x1001pixelimage.Theﬁrst8000pulses(almost4seconds)wereused,andnowindowingwasappliedtothedatabeforeimaging.ThecalculatedmaximumscenesizeisWr=89.94m;Wx=2,032.41m,andthecalculatedresolutionisδr=0.23m;δx=0.25m.Therelativelysmallrangeextentaccountsfortheblackareasintheimage.5.4CivilianVehicleRadarDataDomesIn2010,TheOhioStateUniversityreleasedasetofsyntheticallygenerateddatadomesofciviliantargets.24Thescatteredﬁelddataforthetargetswascomputedforfullazimuthcoverageofelevationanglesfrom30◦to60◦.Thedataisfullpolarimetricwithafrequencybandwidthof5.35GHzatacenterfrequencyof9.6GHz.Thebackprojectionalgorithmwasimplementedonthe1993Jeeptarget,andaresultingimageisshowninFigure5.Thedataimagedconsistedofall360◦aspectanglesfromasingleelevationof30◦usingVVpolarization.Thefullbandwidthwasusedtoformtheimage.Thesceneextentis10mx10mwith2cmpixelspacing,resultingina501x501pixelimage.Nowindowingwasappliedtothedatabeforeimaging.ThecalculatedmaximumscenesizeisWr=14.30m;Wx=11.18m.

分享到：

赞收藏

资料库

SAR image formation toolbox for MATLAB.pdf

相关推荐

课程资源

热门标签

最新资料