第1页 / 共8页
第2页 / 共8页
第3页 / 共8页
第4页 / 共8页
第5页 / 共8页
第6页 / 共8页
第7页 / 共8页
第8页 / 共8页
直线圆与椭圆的绘制.docx
实验二 直线、圆与椭圆的绘制
实验二 直线、圆与椭圆的绘制
一、 实验目的
1．进一步学习使用 Trubo C 和 Visual C++的图形功能；
2．理解并掌握直线的 DDA 算法与 Bresenham 算法的原理；
3．比较 DDA 算法与 Bresenham 算法绘制直线的异同，进一步加深理解。
4．理解并掌握圆与椭圆的利用极坐标方程实现的 DDA 算法的原理
5．理解并掌握圆的 Bresenham 算法原理
6. 理解椭圆的中点算法
二、 实验原理
DDA 算法是一个增量算法。增量算法：在一个迭代算法中，每一步的 x、y
值是用前一步的值加上一个增量来获得。
通过各行各列象素中心构造一组虚拟网格线。按直线从起点到终点的顺序计
算直线与各垂直网格线的交点，然后根据误差项的符号确定该列象素中与此交点
最近的象素。
圆的 Bresenham 算法：
以点(0,r)为起点，按顺时针方向生成圆时，相当于在第一象限内，所以 y 是
x 的单调递减函数。y 的计算式为：
2
y
2
r
(
x
i
2
1)
令 d1、d2 分别为 yi 到 y、yi-1 到 y 的距离，可知：
d
d
1
2
d
i
2
2
y
i
y
y
(
2(
x
i
2
y
i
1)
2
2
y
i
1)
2
r
2
y
i
2
2
(
x
i
2
(
x
i
(
y
i
1)
1)
2
1)
r
i
(
y
2
2
r
令判断式 di=d1-d2，并代入 d1、d2，则有：
2
2
1)
（1）如果 di<0，则 y=yi，即选择当前像素的正右方作为下一个像素，递推公式
为：
x
i
y
i
d
i
1
1
1
x
i
y
i
d
i
1
4
x
i
6
（2）如果 di≥0，则 y=yi-1，即选择当前像素的右下方作为下一个像素，递推
公式为：
（3）计算判别式的初值。初始点为（0，R），则：
1
1
4(
x
i
y
i
d
x
i
y
i
d
) 10
y
i
x
i
1
1
1
i
i
2
2
R
3 2
R
d
1)
三、 主要仪器及耗材
R
R
2
(
0
2
2
pc 机
四、 实验内容与步骤
// 定义直线两端点和
1．编程实现直线的 DDA 算法程序；
void CMyView::OnDdaline()
{
CDC *pDC=GetDC();
// 获得设备指针
int x0=100,y0=100,x1=300,y1=200,c=RGB(255,0,0);
直线颜色（红色）
float x,y,i;
float dx,dy,k;
dx=(float)(x1-x0);
dy=(float)(y1-y0);
k=dy/dx;//计算斜率
y=y0; x=x0;
if(abs(k)<1)
{
for(;x<=x1;x++)
{pDC->SetPixel(x,int(y+0.5),c);
y=y+k;}//x 自增，y=y+k
}
if(abs(k)>=1)
{
for(;y<=y1;y++)
{pDC->SetPixel(int(x+0.5),y,c);
x=x+1/k;}
//释放设备指针
}
ReleaseDC(pDC);
}
2．编程实现直线 Bresenham 算法程序及整数 Bresenham 算法程序；
直线的 Bresenham 算法实现：
void CTestView ::OnBresenhamline()
{
CDC *pDC=GetDC();
int x1=100,y1=200,x2=600,y2=800,color=RGB(0,0,255);
int i,x,y,dx,dy;
float k,e;
dx=x2-x1;
dy=y2-y1;
k=dy/dx;
e=-0.5;
for(i=0;i<=dx;i++)
y=y1;//e 初值 d0-0.5
x=x1;
{ y++; e=e-1;}
pDC->SetPixel(x,y,color);
{
x++;
e=e+k;
if(e>=0)
}
}
直线的整数 Bresenham 算法实现：
void CTestView::OnBresenhamline()
{
CDC *pDC=GetDC();
int x0=100,y0=100,x1=500,y1=600,color=RGB(0,0,255); int i,x,y,dx,dy;
float k,e;
dx=x1-x0;
dy=y1-y0;
e=-dx;
x=x0; y=y0;
for(i=0;i<=dx;i++)
{
pDC->SetPixel(x,y,color);
x++;
e+=2*dy;
if(e>=0)
{ y++;e=e-2*dx;} }
ReleaseDC(pDC);
}
3．编程实现圆的 Bresenham 算法程序；
圆的 Bresenham 算法实现：
void CMyView::OnBresenhamcircle()
{
CDC *pDC=GetDC();
int x0=100,y0=100,x,y,r=80,c=0; //黑色圆弧
float e,d;
e=3-2*r;x=0;y=r;
while(x<=y)
{
if (e<0)
{e=e+4*x+6;x++;}
else{e=e+4*(x-y)+10; x++;y--;}
pDC->SetPixel(x+x0,y+y0,c);//8 对称画圆
pDC->SetPixel(-x+x0,y+y0,c);
pDC->SetPixel(-x+x0,-y+y0,c);
pDC->SetPixel(x+x0,-y+y0,c);
pDC->SetPixel(y+x0,x+y0,c);
pDC->SetPixel(-y+x0,x+y0,c);
pDC->SetPixel(-y+x0,-x+y0,c);
pDC->SetPixel(y+x0,-x+y0,c);
}
ReleaseDC(pDC);
}
4.椭圆的中点算法实现：
void CTestView::OnMidpointellispe()
{
CDC *pDC=GetDC();
int a=100,b=300,x,y,color=50;
float d1,d2;
x=0;y=b;
d1=b*b+a*a*(-b+0.25);
pDC->SetPixel(x,y,color);
pDC->SetPixel(-x,-y,color);
pDC->SetPixel(-x,y,color);
pDC->SetPixel(x,-y,color);
while(b*b*(x+1)SetPixel(x,y,color);
pDC->SetPixel(-x,-y,color);
pDC->SetPixel(-x,y,color);
pDC->SetPixel(x,-y,color);
}/*while 上半部分*/
d2=b*b*(x+0.5)*(x+0.5)+a*a*(y-1)*(y-1)-a*a*b*b;
while(y>0)
{
if(d2<=0) {
d2+=b*b*(2*x+2)+a*a*(-2*y+3);
x++; y--; }
else { d2+=a*a*(-2*y+3);y--; }
pDC->SetPixel(x,y,color);
pDC->SetPixel(-x,-y,color);
pDC->SetPixel(-x,y,color);
pDC->SetPixel(x,-y,color);
}
}
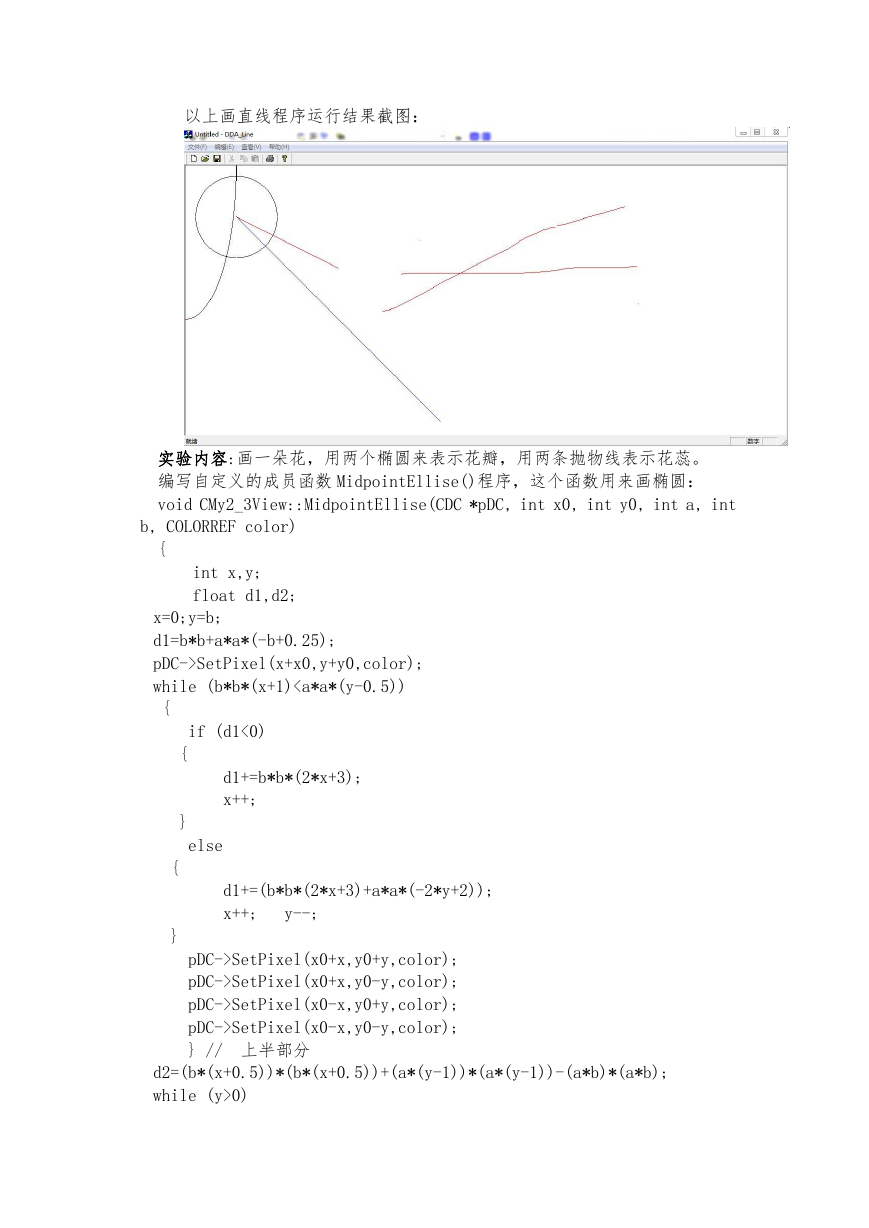
以上画直线程序运行结果截图：
实验内容:画一朵花，用两个椭圆来表示花瓣，用两条抛物线表示花蕊。
编写自定义的成员函数 MidpointEllise()程序，这个函数用来画椭圆：
void CMy2_3View::MidpointEllise(CDC *pDC, int x0, int y0, int a, int
b, COLORREF color)
{
int x,y;
float d1,d2;
x=0;y=b;
d1=b*b+a*a*(-b+0.25);
pDC->SetPixel(x+x0,y+y0,color);
while (b*b*(x+1)SetPixel(x0+x,y0+y,color);
pDC->SetPixel(x0+x,y0-y,color);
pDC->SetPixel(x0-x,y0+y,color);
pDC->SetPixel(x0-x,y0-y,color);
} // 上半部分
d2=(b*(x+0.5))*(b*(x+0.5))+(a*(y-1))*(a*(y-1))-(a*b)*(a*b);
while (y>0)
{
if (d2<0)
{
}
{
}
d2+=b*b*(2*x+2)+a*a*(-2*y+3);
x++;
y--;
else
d2+=a*a*(-2*y+3);
y--;
pDC->SetPixel(x0+x,y0+y,color);
pDC->SetPixel(x0+x,y0-y,color);
pDC->SetPixel(x0-x,y0+y,color);
pDC->SetPixel(x0-x,y0-y,color);
} //下半部分
}
编写自定义的的成员函数 PositiveNegativeParabola()程序，这个函数用来画
花蕊：
void CMy2_3View::PositiveNegativeParabola(CDC *pDC, float a, float b,
float c, int color)
{
{
int x,y,d;
x=0;
y=0;
pDC->SetPixel(x+450+b,y+225+c,color);
if(a>0)
y=1;
pDC->SetPixel(x+450+b,y+225+c,color);
d=1;
while(y<=30)
{
if(d>=0)
{
}
d=d-2*a*x-a;
x++;
else
{
}
d=d+1;
y++;
pDC->SetPixel(-x+450+b,y+225+c,color);
pDC->SetPixel(x+450+b,y+225+c,color);
}
}
else if(a<0)
{
x=1;
pDC->SetPixel(x+450+b,y+225+c,color);
d=1;
while(y>=-35)
{
if(d>=0)
{
}
{
}
d=d-1;
y--;
else
d=d-2*a*x-a;
x++;
pDC->SetPixel(-x+450+b,y+225+c,color);
pDC->SetPixel(x+450+b,y+225+c,color);
}
else
{
}
printf("this is not a Parabola!\n");
}
}
编写 OnDraw()函数程序：
void CMy2_3View::OnDraw(CDC* pDC)
{
CMy2_3Doc* pDoc = GetDocument();
ASSERT_VALID(pDoc);
// TODO: add draw code for native data here
MidpointEllise(pDC, 430, 220, 100, 40, RGB(255,0,0));
MidpointEllise(pDC, 430, 220, 40, 100, RGB(255,0,0));
PositiveNegativeParabola(pDC,-0.7,-20,3,RGB(255,0,0));
PositiveNegativeParabola(pDC,-0.1,-20,3,RGB(255,0,0));
}
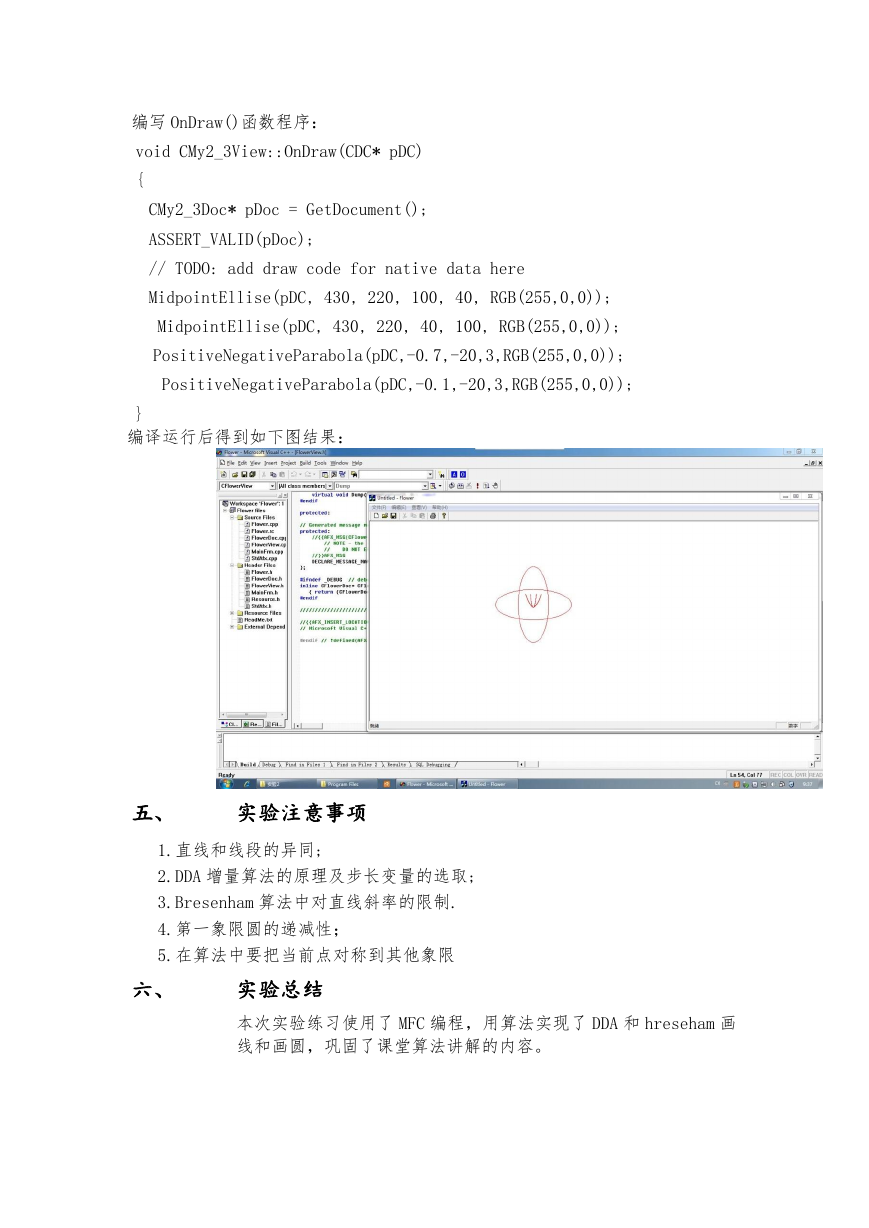
编译运行后得到如下图结果：
五、
实验注意事项
1.直线和线段的异同;
2.DDA 增量算法的原理及步长变量的选取;
3.Bresenham 算法中对直线斜率的限制.
4.第一象限圆的递减性；
5.在算法中要把当前点对称到其他象限
六、
实验总结
本次实验练习使用了 MFC 编程，用算法实现了 DDA 和 hreseham 画
线和画圆，巩固了课堂算法讲解的内容。
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
