第1页 / 共4209页
第2页 / 共4209页
第3页 / 共4209页
第4页 / 共4209页
第5页 / 共4209页
第6页 / 共4209页
第7页 / 共4209页
第8页 / 共4209页
Encyclopedia of Actuarial Science 精算科学百科全书.pdf
cover
1. Claims Distributions
Aggregate Loss Modeling.pdf
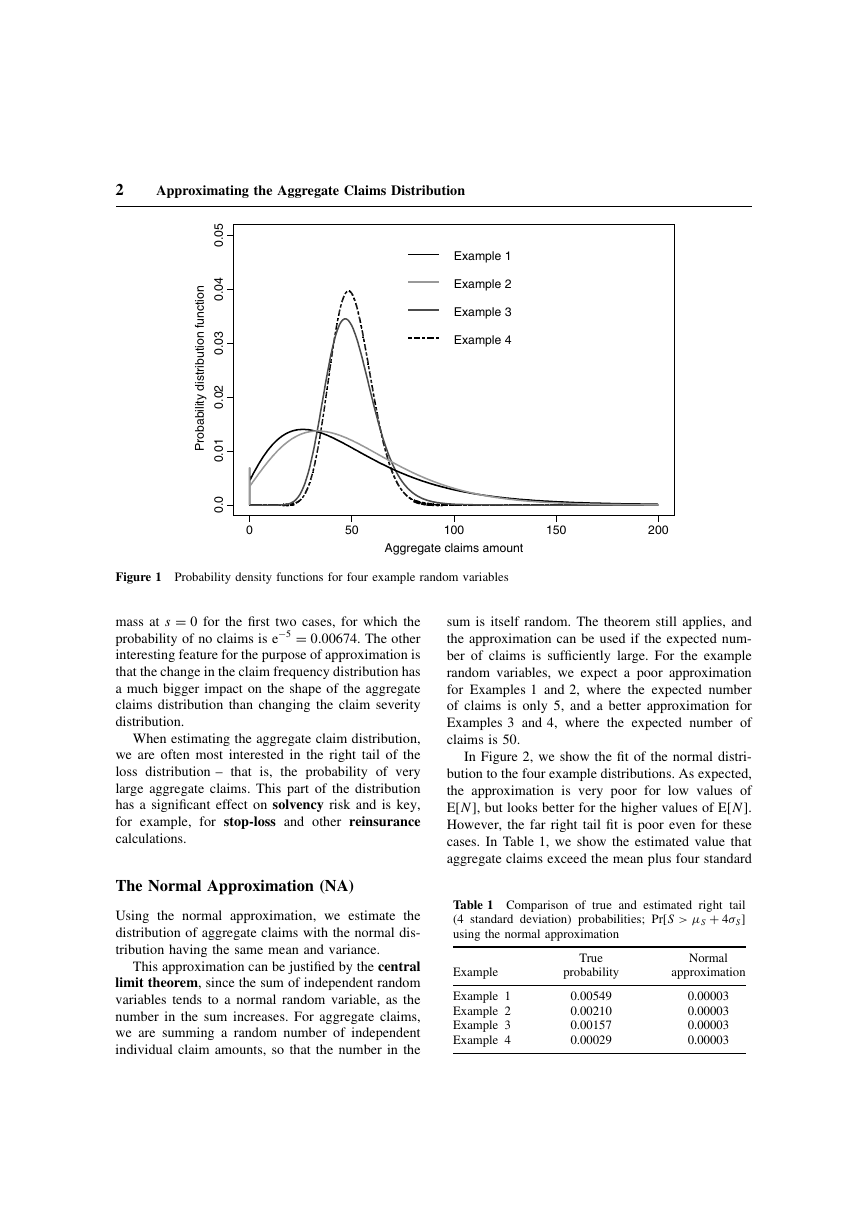
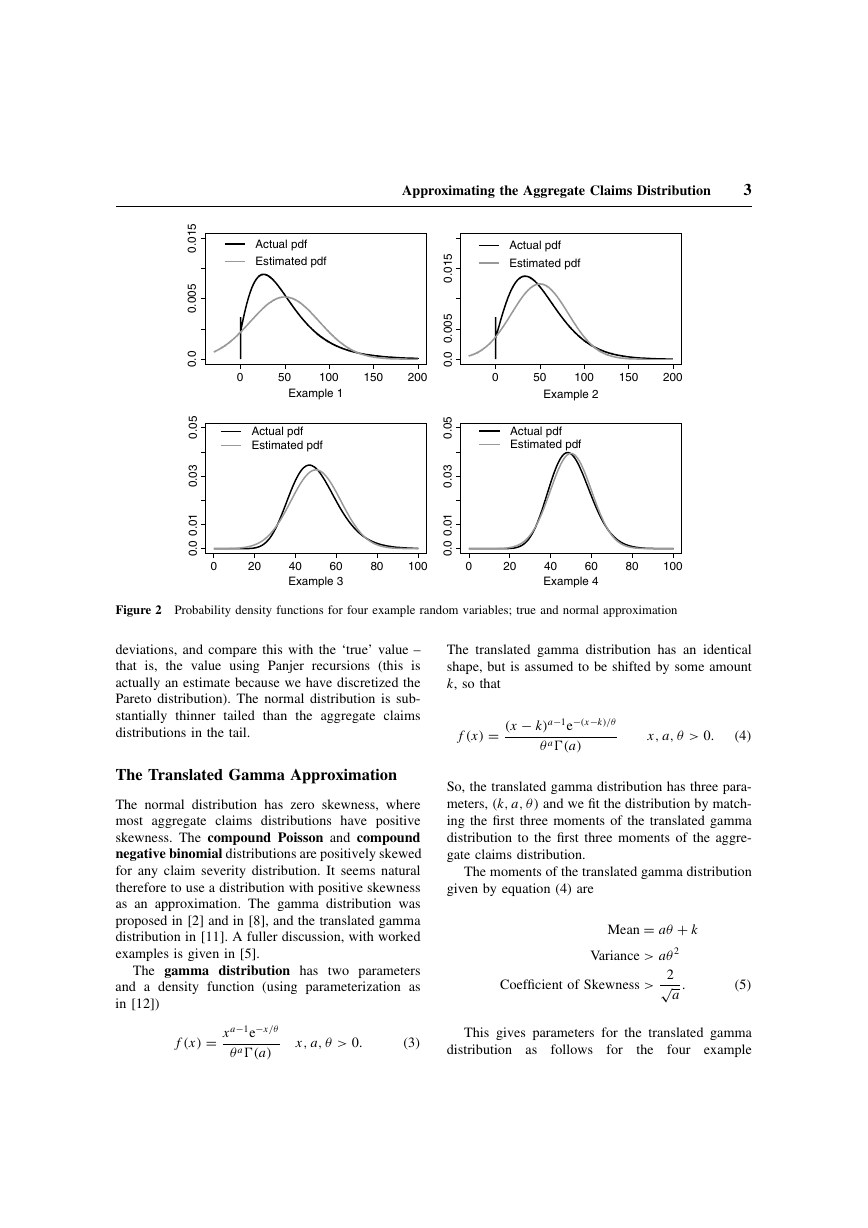
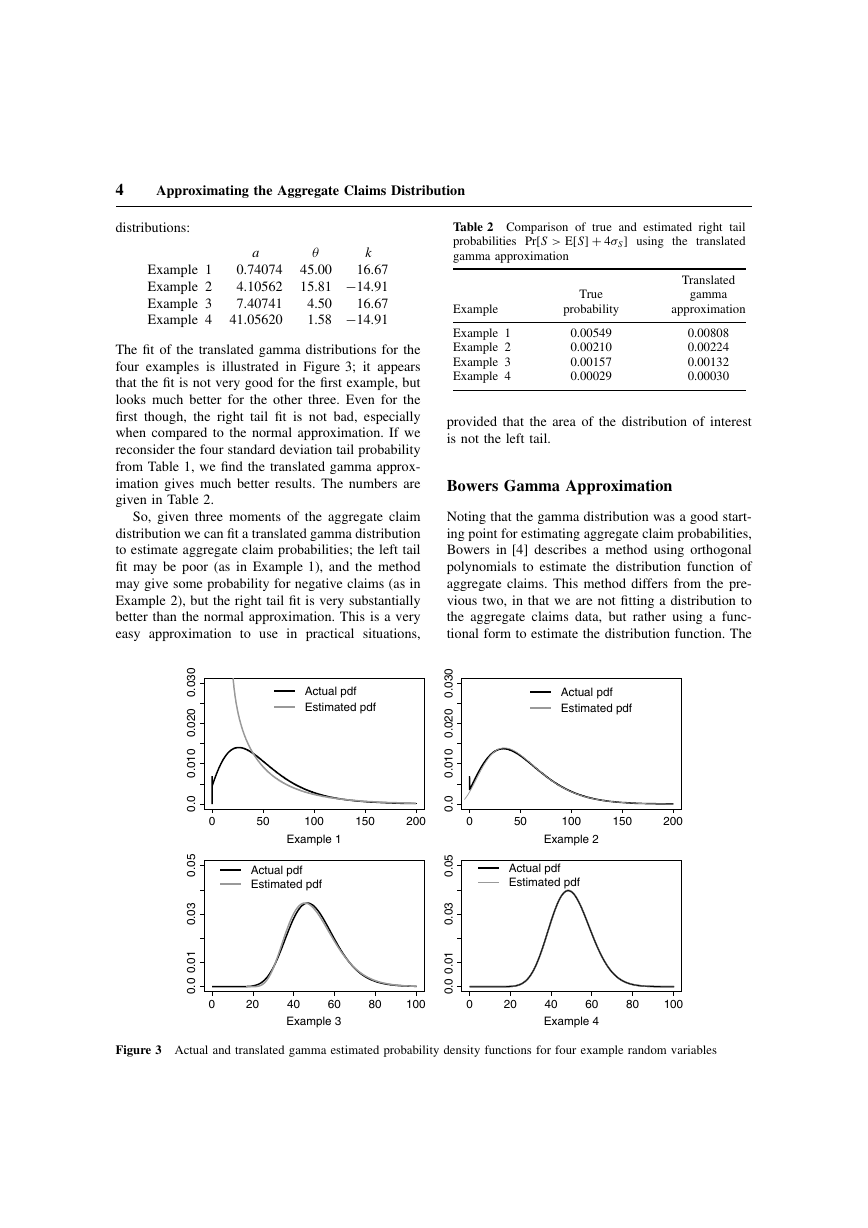
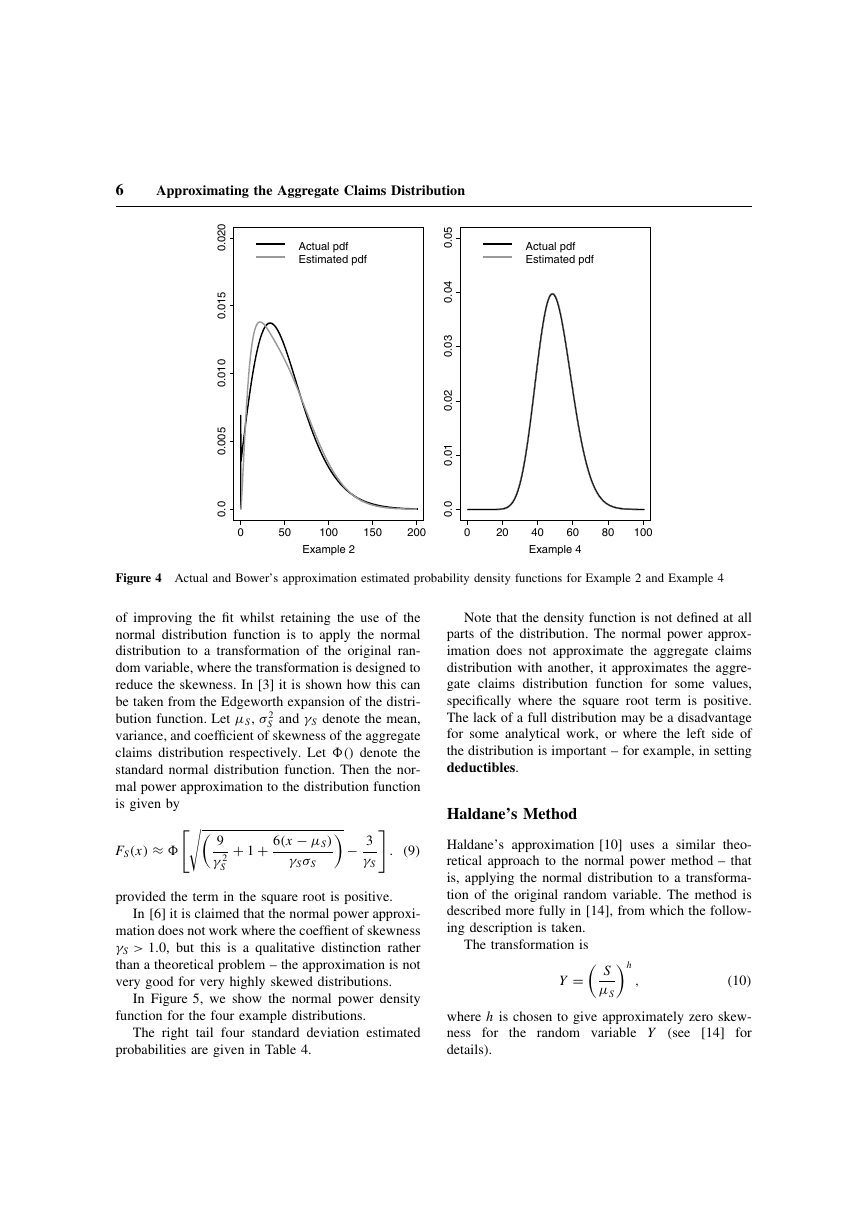
Approximating the Aggregate Claims Distribution.pdf
Bailey–Simon Method.pdf
Beekman’s Convolution Formula.pdf
Beta Function.pdf
Censored Distributions.pdf
Claim Size Processes.pdf
Collective Risk Models.pdf
Collective Risk Theory.pdf
Comonotonicity.pdf
Compound Distributions.pdf
Compound Poisson Frequency Models.pdf
Compound Process.pdf
Continuous Multivariate Distributions.pdf
Continuous Parametric Distributions.pdf
Convolutions of Distributions.pdf
Copulas.pdf
Cramer-Lundberg Asymptotics.pdf
Cramer-Lundberg Condition and Estimate.pdf
Credit Risk.pdf
De Pril Recursions and Approximations.pdf
Dependent Risks.pdf
Discrete Multivariate Distributions.pdf
Discrete Parametric Distributions.pdf
Discretization of Distributions.pdf
Empirical Distribution.pdf
Esscher Transform.pdf
Estimation.pdf
Extreme Value Distributions.pdf
Extreme Value Theory.pdf
Failure Rate.pdf
Gamma Function.pdf
Generalized Discrete Distributions.pdf
Heckman-Meyers Algorithm.pdf
Individual Risk Model.pdf
Inflation Impact on Aggregate Claims.pdf
Integrated Tail Distribution.pdf
Largest Claims and ECOMOR Reinsurance.pdf
Levy Processes.pdf
Lundberg Approximations, Generalized.pdf
Lundberg Inequality for Ruin Probability.pdf
Markov Chain Monte Carlo Methods.pdf
Mean Residual Lifetime.pdf
Mixed Poisson Distributions.pdf
Mixture of Distributions.pdf
Mixtures of Exponential Distributions.pdf
Options and Guarantees in Life Insurance.pdf
Ordering of Risks.pdf
Pareto Rating.pdf
Phase Method.pdf
Phase-type Distributions.pdf
Reliability Classifications.pdf
Retention and Reinsurance Programmes.pdf
Ruin Theory.pdf
Scale Distribution.pdf
Seasonality.pdf
Severity of Ruin.pdf
Stationary Processes.pdf
Stop-loss Premium.pdf
Stop-loss Reinsurance.pdf
Subexponential Distributions.pdf
Sundt and Jewell Class of Distributions.pdf
Sundt’s Classes of Distributions.pdf
Thinned Distributions.pdf
Time of Ruin.pdf
Truncated Distributions.pdf
Value-at-risk.pdf
Zero-modified Frequency Distributions.pdf
2. Collective Risk Theory
Adjustment Coefficient.pdf
Aggregate Loss Modeling.pdf
Ammeter Process.pdf
Ammeter, Hans (1912–1986).pdf
Approximating the Aggregate Claims Distribution.pdf
Bayesian Claims Reserving.pdf
Beekman’s Convolution Formula.pdf
Brownian Motion.pdf
Change of Measure.pdf
Claim Number Processes.pdf
Collective Risk Models.pdf
Collective Risk Theory.pdf
Comonotonicity.pdf
Compound Distributions.pdf
Compound Poisson Frequency Models.pdf
Compound Process.pdf
Convolutions of Distributions.pdf
Counting Processes.pdf
Coverage.pdf
Cramer, Harald (1893–1985).pdf
Cramer-Lundberg Asymptotics.pdf
Cramer-Lundberg Condition and Estimate.pdf
De Pril Recursions and Approximations.pdf
Dependent Risks.pdf
Diffusion Approximations.pdf
Dividends.pdf
Early Warning Systems.pdf
Esscher Transform.pdf
Financial Insurance.pdf
Gaussian Processes.pdf
Generalized Discrete Distributions.pdf
Heckman-Meyers Algorithm.pdf
Individual Risk Model.pdf
Integrated Tail Distribution.pdf
Large Deviations.pdf
Lundberg Approximations, Generalized.pdf
Lundberg Inequality for Ruin Probability.pdf
Markov Chains and Markov Processes.pdf
Markov Models in Actuarial Science.pdf
Mean Residual Lifetime.pdf
Mixtures of Exponential Distributions.pdf
Nonparametric Statistics.pdf
Occurrence-Exposure Rate.pdf
Operational Time.pdf
Phase Method.pdf
Point Processes.pdf
Poisson Processes.pdf
Reliability Classifications.pdf
Renewal Theory.pdf
Retrospective Premium.pdf
Risk Management- An Interdisciplinary Framework.pdf
Risk Measures.pdf
Risk Minimization.pdf
Risk Process.pdf
Ruin Theory.pdf
Seasonality.pdf
Segerdahl, Carl–Otto (1912–1972).pdf
Severity of Ruin.pdf
Shot-noise Processes.pdf
Simulation of Risk Processes.pdf
Solvency.pdf
Stability.pdf
Stochastic Simulation.pdf
Stop-loss Premium.pdf
Subexponential Distributions.pdf
Surplus Process.pdf
Time of Ruin.pdf
3. Direct Nonlife Insurance
Accident Insurance.pdf
Accounting.pdf
Actuary.pdf
Affine Models of the Term Structure of Interest Rates.pdf
Aggregate Loss Modeling.pdf
ALAE.pdf
Annual Statements.pdf
Antiselection, Non-life.pdf
Aquaculture Insurance.pdf
ASTIN.pdf
Automobile Insurance, Commercial.pdf
Automobile Insurance, Private.pdf
Aviation Insurance.pdf
Beard, Robert Eric (1911–1983).pdf
Bonus-Malus Systems.pdf
Bundling.pdf
Burglary Insurance.pdf
Captives.pdf
Casualty Actuarial Society.pdf
Catastrophe Excess of Loss.pdf
Claim Frequency.pdf
Claim Number Processes.pdf
Closed Claim.pdf
Coinsurance.pdf
Combined Ratio.pdf
Commercial Multi-peril Insurance.pdf
Consequential Damage.pdf
Cooperative Game Theory.pdf
Coverage.pdf
Crop Insurance.pdf
Deductible.pdf
Demutualization.pdf
Dependent Risks.pdf
Deregulation of Commercial Insurance.pdf
DFA - Dynamic Financial Analysis.pdf
Duration.pdf
Dynamic Financial Modeling of an Insurance Enterprise.pdf
Earthquake Insurance.pdf
Employer’s Liability Insurance.pdf
Employment Practices Liability Insurance.pdf
Expense Ratios.pdf
Fidelity and Surety.pdf
Financial Engineering.pdf
Financial Insurance.pdf
Fire Insurance.pdf
Flood Risk.pdf
Franckx, Edouard (1907–1988).pdf
Fraud in Insurance.pdf
History of Insurance.pdf
Homeowners Insurance.pdf
Insurance Company.pdf
Insurance Forms.pdf
Insurance Regulation and Supervision.pdf
Lapses.pdf
Leverage.pdf
Liability Insurance.pdf
Lloyd’s.pdf
Long-tail Business.pdf
Loss Ratio.pdf
Loss-of-Profits Insurance.pdf
Marine Insurance.pdf
Mass Tort Liabilities.pdf
Mortgage Insurance in the United States.pdf
Mutuals.pdf
Natural Hazards.pdf
Non-life Insurance.pdf
P&I Clubs.pdf
Policy.pdf
Pooling in Insurance.pdf
Premium.pdf
Property Insurance - Personal.pdf
Ratemaking.pdf
Replacement Value.pdf
Reserving in Non-life Insurance.pdf
Risk Classification, Practical Aspects1.pdf
Risk Classification, Pricing Aspects.pdf
Risk Statistics.pdf
Self-insurance.pdf
Sickness Insurance.pdf
Total Loss.pdf
Travel Insurance.pdf
Unemployment Insurance.pdf
Workers’ Compensation Insurance.pdf
4. Economics
Adverse Selection.pdf
Audit.pdf
Background Risk.pdf
Borch, Karl Henrik (1919–1986).pdf
Borch’s Theorem.pdf
Capital Allocation for P&C Insurers- A Survey of Methods.pdf
Collective Risk Theory.pdf
Complete Markets.pdf
Convexity.pdf
Cooperative Game Theory.pdf
De Finetti, Bruno (1906–1985).pdf
Decision Theory.pdf
Deregulation of Commercial Insurance.pdf
Derivative Securities.pdf
DFA - Dynamic Financial Analysis.pdf
Efficient Markets Hypothesis.pdf
Equilibrium Theory.pdf
Finance.pdf
Financial Economics.pdf
Financial Intermediaries- the Relationship Between their Economic Functions and Actuarial Risks.pdf
Financial Markets.pdf
Fraud in Insurance.pdf
Free Riding.pdf
Frontier Between Public and Private Insurance Schemes.pdf
Incomplete Markets.pdf
Insolvency.pdf
Insurability.pdf
Lotteries.pdf
Market Equilibrium.pdf
Moral Hazard.pdf
Noncooperative Game Theory.pdf
Nonexpected Utility Theory.pdf
Oligopoly in Insurance Markets.pdf
Operations Research.pdf
Optimal Risk Sharing.pdf
Ordering of Risks.pdf
Pareto Optimality.pdf
Pooling Equilibria.pdf
Pooling in Insurance.pdf
Portfolio Theory.pdf
Premium Principles.pdf
Reinsurance Forms.pdf
Retention and Reinsurance Programmes.pdf
Risk Aversion.pdf
Risk Management- An Interdisciplinary Framework.pdf
Risk Measures.pdf
Risk Minimization.pdf
Risk Utility Ranking.pdf
Risk-based Capital Allocation.pdf
Solvency.pdf
Stochastic Control Theory.pdf
Stochastic Orderings.pdf
Underwriting Cycle.pdf
Utility Maximization.pdf
Utility Theory.pdf
Wilkie Investment Model.pdf
5. Finance
Accounting.pdf
Affine Models of the Term Structure of Interest Rates.pdf
AFIR.pdf
Alternative Risk Transfer.pdf
Arbitrage.pdf
Asset Management.pdf
Asset–Liability Modeling.pdf
Assets in Pension Funds.pdf
Association of Actuaries and Financial Analysts.pdf
Background Risk.pdf
Binomial Model.pdf
Black–Scholes Model.pdf
Brownian Motion.pdf
Capital Allocation for P&C Insurers- A Survey of Methods.pdf
Capital in Life Assurance.pdf
Catastrophe Derivatives.pdf
Change of Measure.pdf
Collective Investment (Pooling).pdf
Complete Markets.pdf
Credit Risk.pdf
Credit Scoring.pdf
Derivative Pricing, Numerical Methods.pdf
Derivative Securities.pdf
DFA - Dynamic Financial Analysis.pdf
Diffusion Processes.pdf
Dynamic Financial Modeling of an Insurance Enterprise.pdf
Early Warning Systems.pdf
Efficient Markets Hypothesis.pdf
Equilibrium Theory.pdf
Esscher Transform.pdf
Finance.pdf
Financial Economics.pdf
Financial Engineering.pdf
Financial Intermediaries- the Relationship Between their Economic Functions and Actuarial Risks.pdf
Financial Markets.pdf
Financial Pricing of Insurance.pdf
Financial Reinsurance.pdf
Fixed-income Security.pdf
Foreign Exchange Risk in Insurance.pdf
Hedging and Risk Management.pdf
Hidden Markov Models.pdf
History of Actuarial Profession.pdf
Incomplete Markets.pdf
Index-linked Security.pdf
Inflation- A Case Study.pdf
Insolvency.pdf
Insurability.pdf
Interest-rate Modeling.pdf
Interest-rate Risk and Immunization.pdf
Ito Calculus.pdf
Life Insurance.pdf
Life Reinsurance.pdf
Logistic Regression Model.pdf
Market Equilibrium.pdf
Market Models.pdf
Martingales.pdf
Matching.pdf
Model Office.pdf
Noncooperative Game Theory.pdf
Options and Guarantees in Life Insurance.pdf
Ornstein-Uhlenbeck Process.pdf
Participating Business.pdf
Pensions.pdf
Portfolio Theory.pdf
Premium Principles.pdf
Present Values and Accumulations.pdf
Profit Testing.pdf
Redington, Frank Mitchell (1906–1984).pdf
Reinsurance – Terms, Conditions, and Methods of Placing.pdf
Reinsurance Supervision.pdf
Reinsurance1.pdf
Untitled
Risk Measures.pdf
Risk-based Capital Requirements.pdf
Self-insurance.pdf
Shot-noise Processes.pdf
Simulation Methods for Stochastic Differential Equations.pdf
Stochastic Control Theory.pdf
Stochastic Investment Models.pdf
Surplus in Life and Pension Insurance.pdf
Time Series.pdf
Transaction Costs.pdf
Underwriting Cycle.pdf
Unit-linked Business.pdf
Utility Maximization.pdf
Valuation of Life Insurance Liabilities.pdf
Value-at-risk.pdf
Volatility.pdf
Wilkie Investment Model.pdf
6. Life, Pension and Health Insurance
Accident Insurance.pdf
Actuarial Control Cycle.pdf
Actuary.pdf
American Society of Pension Actuaries.pdf
Annuities.pdf
Asset Management.pdf
Asset Shares.pdf
Assets in Pension Funds.pdf
Capital in Life Assurance.pdf
Censored Distributions.pdf
Censoring.pdf
Cohort.pdf
Commutation Functions.pdf
Competing Risks.pdf
De Moivre, Abraham (1667–1754).pdf
De Witt, Johan (1625–1672).pdf
Decrement Analysis.pdf
Demography.pdf
Dependent Risks.pdf
Disability Insurance.pdf
Disability Insurance,Numerical Methods
Dodson, James (1710–1757).pdf
Dynamic Financial Modeling of an Insurance Enterprise.pdf
Early Mortality Tables.pdf
Early Warning Systems.pdf
Estate.pdf
Euler–Maclaurin Expansion and Woolhouse’s Formula.pdf
Frailty.pdf
Fraud in Insurance.pdf
Genetics and Insurance.pdf
Gompertz, Benjamin (1779–1865).pdf
Graduation.pdf
Graunt, John (1620–1674).pdf
Group Life Insurance.pdf
Halley, Edmond (1656–1742).pdf
Hattendorff’s Theorem.pdf
Health Insurance.pdf
Heterogeneity in Life Insurance.pdf
History of Actuarial Education.pdf
History of Actuarial Profession.pdf
History of Insurance.pdf
International Actuarial Notation.pdf
Lexis Diagram.pdf
Lidstone, George James (1870–1952).pdf
Lidstone’s Theorem.pdf
Life Insurance.pdf
Life Table Data, Combining.pdf
Life Table.pdf
Linton, Morris Albert (1887–1966).pdf
Long-term Care Insurance.pdf
Lundberg, Filip (1876–1965).pdf
Markov Models in Actuarial Science.pdf
Mass Tort Liabilities.pdf
Maturity Guarantees Working Party.pdf
Maximum Likelihood.pdf
Model Office.pdf
Mortality Laws.pdf
Options and Guarantees in Life Insurance.pdf
Participating Business.pdf
Pension Fund Mathematics.pdf
Pensions- Finance, Risk and Accounting.pdf
Pensions, Individual.pdf
Pensions.pdf
Present Values and Accumulations.pdf
Price, Richard (1723–1791).pdf
Profit Testing.pdf
Risk Classification, Pricing Aspects.pdf
Risk-based Capital Requirements.pdf
Sickness Insurance.pdf
Social Security.pdf
Surplus in Life and Pension Insurance.pdf
Surrenders and Alterations.pdf
Technical Bases in Life Insurance.pdf
Unit-linked Business.pdf
Valuation of Life Insurance Liabilities.pdf
Waring’s Theorem.pdf
Wilkie Investment Model.pdf
7. Organizations, Journals and History
Actuarial Institute of the Republic of China.pdf
Actuarial Research Clearing House (ARCH).pdf
Actuarial Society of Ghana.pdf
Actuarial Society of Hong Kong.pdf
Actuary.pdf
AFIR.pdf
Aktuarvereinigung Osterreichs (Austrian Actuarial Association).pdf
American Academy of Actuaries.pdf
American Risk and Insurance Association (ARIA).pdf
American Society of Pension Actuaries.pdf
Ammeter, Hans (1912–1986).pdf
Argentina, Actuarial Associations.pdf
Association of Actuaries and Financial Analysts.pdf
Association Royale des Actuaires Belges.pdf
ASTIN.pdf
Bailey, Arthur L. (1905–1954).pdf
Beard, Robert Eric (1911–1983).pdf
Bernoulli Family.pdf
Borch, Karl Henrik (1919–1986).pdf
Brazilian Institute of Actuaries (IBA).pdf
British Actuarial Journal.pdf
Canadian Institute of Actuaries.pdf
Casualty Actuarial Society.pdf
Ceska Spolecnost Aktuaru (The Czech Society of Actuaries).pdf
China, Development of Actuarial Science.pdf
Col-legi d’Actuaris de Catalunya.pdf
Combinatorics.pdf
Competing Risks.pdf
Conference of Consulting Actuaries.pdf
Cramer, Harald (1893–1985).pdf
Croatian Actuarial Association.pdf
Cyprus Association of Actuaries (CAA).pdf
De Finetti, Bruno (1906–1985).pdf
De Moivre, Abraham (1667–1754).pdf
De Witt, Johan (1625–1672).pdf
Decrement Analysis.pdf
Demography.pdf
Den Danske Aktuarforening (The Danish Society of Actuaries).pdf
Den Norske Aktuarforening (The Norwegian Society of Actuaries).pdf
Deutsche Aktuarvereinigung e. V. (DAV).pdf
Dodson, James (1710–1757).pdf
Early Mortality Tables.pdf
Estonian Actuarial Society.pdf
Faculty of Actuaries.pdf
Franckx, Edouard (1907–1988).pdf
Gompertz, Benjamin (1779–1865).pdf
Graduation.pdf
Graphical Methods.pdf
Graunt, John (1620–1674).pdf
Groupe Consultatif Actuariel Europeen.pdf
Halley, Edmond (1656–1742).pdf
Hellenic Actuarial Society.pdf
Het Actuarieel Genootschap (The Dutch Actuarial Society).pdf
History of Actuarial Education.pdf
History of Actuarial Profession.pdf
History of Actuarial Science.pdf
History of Insurance.pdf
Hungarian Actuarial Society.pdf
Huygens, Christiaan and Lodewijck (1629–1695).pdf
I nternational Actuarial Association.pdf
Institut des Actuaires.pdf
Institute of Actuaries of Australia.pdf
Institute of Actuaries of Japan.pdf
Institute of Actuaries.pdf
Insurance Company.pdf
Insurance- Mathematics and Economics.pdf
International Association for the Study of Insurance Economics – ‘The Geneva Association’.pdf
International Association of Consulting Actuaries.pdf
Israel Association of Actuaries.pdf
Istituto Italiano degli Attuari.pdf
Journal of Actuarial Practice.pdf
Latvian Actuarial Association.pdf
Lidstone, George James (1870–1952).pdf
Linton, Morris Albert (1887–1966).pdf
Lloyd’s.pdf
Long-term Care Insurance.pdf
Lotteries.pdf
Lundberg, Filip (1876–1965).pdf
McClintock, Emory (1840–1916).pdf
Mexico, Actuarial Associations.pdf
Mortality Laws.pdf
National Associations of Actuaries.pdf
New Zealand Society of Actuaries.pdf
Pakistan Society of Actuaries.pdf
Persatuan Aktuari Malaysia.pdf
Polskie Stowarzyszenie Aktuariuszy.pdf
Portuguese Institute of Actuaries.pdf
Price, Richard (1723–1791).pdf
Probability Theory.pdf
Professionalism.pdf
Redington, Frank Mitchell (1906–1984).pdf
RESTIN.pdf
Risk-based Capital Requirements.pdf
Rubinow, Isaac Max (1875–1936).pdf
Scandinavian Actuarial Journal.pdf
Segerdahl, Carl–Otto (1912–1972).pdf
Singapore Actuarial Society.pdf
Slovak Society of Actuaries.pdf
Slovensko Aktuarsko Drustvo (The Slovenian Association of Actuaries).pdf
Society of Actuaries.pdf
Suomen Aktuaariyhdistys (The Actuarial Society of Finland).pdf
Svenska Aktuarieforeningen, Swedish Society of Actuaries.pdf
Sverdrup, Erling (1917–1994).pdf
Swiss Association of Actuaries.pdf
Thiele, Thorvald Nicolai (1838–1910).pdf
Ukrainian Actuarial Society.pdf
Utility Theory.pdf
Wright, Elizur (1804–1885).pdf
8. Premium Calculation, Nonlife
Adverse Selection.pdf
Alternative Risk Transfer.pdf
Automobile Insurance, Private.pdf
Bailey–Simon Method.pdf
Bayesian Statistics.pdf
Bonus-Malus Systems.pdf
Burning Cost.pdf
Catastrophe Models and Catastrophe Loads.pdf
Claim Size Processes.pdf
Credibility Theory.pdf
Decision Theory.pdf
Dirichlet Processes.pdf
Disability Insurance.pdf
Discretization of Distributions.pdf
Experience-rating.pdf
Financial Pricing of Insurance.pdf
Foreign Exchange Risk in Insurance.pdf
Fuzzy Set Theory.pdf
Group Life Insurance.pdf
Heterogeneity in Life Insurance.pdf
Homeowners Insurance.pdf
Kalman Filter, Reserving Methods.pdf
Kalman Filter.pdf
Life Insurance.pdf
Long-tail Business.pdf
Nonparametric Statistics.pdf
Nonproportional Reinsurance.pdf
Ordering of Risks.pdf
Premium Principles.pdf
Premium.pdf
Ratemaking.pdf
Reinsurance Pricing.pdf
Retention and Reinsurance Programmes.pdf
Retrospective Premium.pdf
Risk Classification, Practical Aspects1.pdf
Risk Measures.pdf
Risk Utility Ranking.pdf
Stochastic Orderings.pdf
Stop-loss Reinsurance.pdf
9. Probability Theory
Adjustment Coefficient.pdf
Affine Models of the Term Structure of Interest Rates.pdf
Ammeter Process.pdf
Approximating the Aggregate Claims Distribution.pdf
Bayesian Statistics.pdf
Beekman’s Convolution Formula.pdf
Bernoulli Family.pdf
Binomial Model.pdf
Black–Scholes Model.pdf
Bonus-Malus Systems.pdf
Brownian Motion.pdf
Catastrophe Derivatives.pdf
Censoring.pdf
Central Limit Theorem.pdf
Change of Measure.pdf
Collective Risk Models.pdf
Combinatorics.pdf
Competing Risks.pdf
Continuous Multivariate Distributions.pdf
Continuous Parametric Distributions.pdf
Convexity.pdf
Convolutions of Distributions.pdf
Copulas.pdf
Coupling
Coverage.pdf
Cramer, Harald (1893–1985).pdf
Cramer-Lundberg Asymptotics.pdf
Cramer-Lundberg Condition and Estimate.pdf
Credit Scoring.pdf
De Moivre, Abraham (1667–1754).pdf
Decrement Analysis.pdf
Derivative Pricing, Numerical Methods.pdf
Diffusion Approximations.pdf
Dirichlet Processes.pdf
Discrete Multivariate Distributions.pdf
Discrete Parametric Distributions.pdf
Estimation.pdf
Extreme Value Theory.pdf
Extremes.pdf
Failure Rate.pdf
Filtration.pdf
Finance.pdf
Fuzzy Set Theory.pdf
Gaussian Processes.pdf
Generalized Discrete Distributions.pdf
Generalized Linear Models.pdf
Genetics and Insurance.pdf
Hattendorff’s Theorem.pdf
Heckman-Meyers Algorithm.pdf
Hidden Markov Models.pdf
Huygens, Christiaan and Lodewijck (1629–1695).pdf
Inflation Impact on Aggregate Claims.pdf
Information Criteria.pdf
Integrated Tail Distribution.pdf
Interest-rate Modeling.pdf
Ito Calculus.pdf
Large Deviations.pdf
Levy Processes.pdf
Life Insurance Mathematics.pdf
Life Table.pdf
Long Range Dependence.pdf
Lundberg Approximations, Generalized.pdf
Lundberg Inequality for Ruin Probability.pdf
Lundberg, Filip (1876–1965).pdf
Market Models.pdf
Markov Chains and Markov Processes.pdf
Markov Models in Actuarial Science.pdf
Martingales.pdf
Maturity Guarantees Working Party.pdf
Mixed Poisson Distributions.pdf
Mixture of Distributions.pdf
Multivariate Statistics.pdf
Neural Networks.pdf
Non-life Reserves – Continuous-time Micro Models.pdf
Numerical Algorithms.pdf
Operational Time.pdf
Operations Research.pdf
Ornstein-Uhlenbeck Process.pdf
Pension Fund Mathematics.pdf
Phase Method.pdf
Phase-type Distributions.pdf
Point Processes.pdf
Poisson Processes.pdf
Probability Theory.pdf
Queueing Theory.pdf
Random Number Generation and Quasi-Monte Carlo.pdf
Random Variable.pdf
Random Walk.pdf
Rare Event.pdf
Regenerative Processes.pdf
Reliability Analysis.pdf
Reliability Classifications.pdf
Renewal Theory.pdf
Risk Process.pdf
Robustness.pdf
Ruin Theory.pdf
Severity of Ruin.pdf
Shot-noise Processes.pdf
Simulation Methods for Stochastic Differential Equations.pdf
Simulation of Risk Processes.pdf
Simulation of Stochastic Processes.pdf
Stability.pdf
Stationary Processes.pdf
Stochastic Control Theory.pdf
Stochastic Optimization.pdf
Stochastic Orderings.pdf
Stochastic Processes.pdf
Subexponential Distributions.pdf
Surplus Process.pdf
Survival Analysis.pdf
Sverdrup, Erling (1917–1994).pdf
Time Series.pdf
Transforms.pdf
Under- and Overdispersion.pdf
Volatility.pdf
Waring’s Theorem.pdf
Wilkie Investment Model.pdf
10. Reinsurance
Alternative Risk Transfer.pdf
Audit.pdf
Aviation Insurance.pdf
Bernoulli Family.pdf
Borch’s Theorem.pdf
Burning Cost.pdf
Captives.pdf
Catastrophe Derivatives.pdf
Catastrophe Excess of Loss.pdf
Catastrophe Models and Catastrophe Loads.pdf
Coinsurance.pdf
Crop Insurance.pdf
De Finetti, Bruno (1906–1985).pdf
Deductible.pdf
DFA - Dynamic Financial Analysis.pdf
Excess-of-loss Reinsurance.pdf
Exposure Rating.pdf
Extreme Value Distributions.pdf
Extremes.pdf
Financial Reinsurance.pdf
Fire Insurance.pdf
Fluctuation Reserves.pdf
Health Insurance.pdf
Largest Claims and ECOMOR Reinsurance.pdf
Life Reinsurance.pdf
Loss Ratio.pdf
Marine Insurance.pdf
Mortgage Insurance in the United States.pdf
Nonexpected Utility Theory.pdf
Non-life Insurance.pdf
Nonparametric Statistics.pdf
Nonproportional Reinsurance.pdf
Optimal Risk Sharing.pdf
P&I Clubs.pdf
Pareto Rating.pdf
Pooling in Insurance.pdf
Pooling of Employee Benefits.pdf
Profit Testing.pdf
Proportional Reinsurance.pdf
Quota-share Reinsurance.pdf
Reinsurance – Terms, Conditions, and Methods of Placing.pdf
Reinsurance Forms.pdf
Reinsurance Pricing.pdf
Reinsurance Supervision.pdf
Reinsurance, Functions and Values1.pdf
Reinsurance, Reserving.pdf
Reinsurance1.pdf
Untitled
RESTIN.pdf
Retention and Reinsurance Programmes.pdf
Risk Management- An Interdisciplinary Framework.pdf
Stop-loss Premium.pdf
Stop-loss Reinsurance.pdf
Surplus Treaty.pdf
Working Covers.pdf
11. Reserving, Nonlife
Accident Insurance.pdf
Accounting.pdf
Actuary.pdf
Annual Statements.pdf
Assets in Pension Funds.pdf
Automobile Insurance, Commercial.pdf
Aviation Insurance.pdf
Bayesian Claims Reserving.pdf
Bornhuetter-Ferguson Method.pdf
Captives.pdf
Catastrophe Models and Catastrophe Loads.pdf
Chain-ladder Method.pdf
Claim Frequency.pdf
Claims Reserving using Credibility Methods.pdf
Combined Ratio.pdf
Consequential Damage.pdf
Disability Insurance.pdf
Duration.pdf
Dynamic Financial Modeling of an Insurance Enterprise.pdf
Experience-rating.pdf
Financial Economics.pdf
Financial Insurance.pdf
Financial Reinsurance.pdf
Fire Insurance.pdf
Fluctuation Reserves.pdf
Generalized Linear Models.pdf
Health Insurance.pdf
Inflation- A Case Study.pdf
Insurance Company.pdf
Insurance Forms.pdf
Kalman Filter, Reserving Methods.pdf
Leverage.pdf
Long-tail Business.pdf
Marine Insurance.pdf
Non-life Reserves – Continuous-time Micro Models.pdf
Pooling of Employee Benefits.pdf
Premium.pdf
Ratemaking.pdf
Reinsurance Supervision.pdf
Reinsurance, Reserving.pdf
Reserving in Non-life Insurance.pdf
Separation Method.pdf
Workers’ Compensation Insurance.pdf
12. Statistics
Bailey, Arthur L. (1905–1954).pdf
Bailey–Simon Method.pdf
Bayesian Claims Reserving.pdf
Bayesian Statistics.pdf
Borch, Karl Henrik (1919–1986).pdf
Bornhuetter-Ferguson Method.pdf
Censoring.pdf
Central Limit Theorem.pdf
Claim Number Processes.pdf
Claims Reserving using Credibility Methods.pdf
Cohort.pdf
Competing Risks.pdf
Continuous Multivariate Distributions.pdf
Credibility Theory.pdf
Credit Scoring.pdf
Decision Theory.pdf
Decrement Analysis.pdf
Derivative Pricing, Numerical Methods.pdf
Dirichlet Processes.pdf
Discrete Multivariate Distributions.pdf
Empirical Distribution.pdf
Estimation.pdf
Experience-rating.pdf
Extreme Value Distributions.pdf
Extremes.pdf
Frailty.pdf
Fraud in Insurance.pdf
Fuzzy Set Theory.pdf
Generalized Linear Models.pdf
Graduation.pdf
Graphical Methods.pdf
Hidden Markov Models.pdf
Information Criteria.pdf
Kalman Filter, Reserving Methods.pdf
Kalman Filter.pdf
Life Insurance Mathematics.pdf
Life Table Data, Combining.pdf
Life Table.pdf
Logistic Regression Model.pdf
Maximum Likelihood.pdf
Mixture of Distributions.pdf
Multivariate Statistics.pdf
Neural Networks.pdf
Non-life Reserves – Continuous-time Micro Models.pdf
Nonparametric Statistics.pdf
Numerical Algorithms.pdf
Occurrence-Exposure Rate.pdf
Outlier Detection.pdf
Parameter and Model Uncertainty.pdf
Pareto Rating.pdf
Phase Method.pdf
Prediction.pdf
Probability Theory.pdf
Random Number Generation and Quasi-Monte Carlo.pdf
Rare Event.pdf
Regression Models for Data Analysis.pdf
Reliability Analysis.pdf
Resampling.pdf
Risk Classification, Pricing Aspects.pdf
Risk Statistics.pdf
Robustness.pdf
Screening Methods.pdf
Seasonality.pdf
Separation Method.pdf
Simulation Methods for Stochastic Differential Equations.pdf
Simulation of Risk Processes.pdf
Splines.pdf
Statistical Terminology.pdf
Stochastic Simulation.pdf
Survival Analysis.pdf
Time Series.pdf
Under- and Overdispersion.pdf
Utility Theory.pdf
Value-at-risk.pdf
Aggregate Loss Modeling
One of the primary goals of actuarial risk theory is
the evaluation of the risk associated with a portfo-
lio of insurance contracts over the life of the con-
tracts. Many insurance contracts (in both life and
non-life areas) are short-term. Typically, automobile
insurance, homeowner’s insurance, group life and
health insurance policies are of one-year duration.
One of the primary objectives of risk theory is
to model the distribution of total claim costs for
portfolios of policies, so that business decisions can
be made regarding various aspects of the insurance
contracts. The total claim cost over a fixed time
period is often modeled by considering the frequency
of claims and the sizes of the individual claims
separately.
Let X1, X2, X3, . . . be independent and identically
distributed random variables with common distribu-
tion function FX(x). Let N denote the number of
claims occurring in a fixed time period. Assume that
the distribution of each Xi, i = 1, . . . , N, is indepen-
dent of N for fixed N. Then the total claim cost for
the fixed time period can be written as
S = X1 + X2 + ··· + XN ,
with distribution function
∞
FS (x) =
n=0
∗n
X (x),
pnF
(1)
X (·) indicates the n-fold convolution of
∗n
where F
FX(·).
The distribution of the random sum given by equa-
tion (1) is the direct quantity of interest to actuaries
for the development of premium rates and safety
margins. In general, the insurer has historical data on
the number of events (insurance claims) per unit time
period (typically one year) for a specific risk, such
as a given driver/car combination (e.g. a 21-year-old
male insured in a Porsche 911). Analysis of this data
generally reveals very minor changes over time. The
insurer also gathers data on the severity of losses per
event (the X ’s in equation (1)). The severity varies
over time as a result of changing costs of automobile
repairs, hospital costs, and other costs associated with
losses.
Data is gathered for the entire insurance industry
in many countries. This data can be used to develop
models for both the number of claims per time period
and the number of claims per insured. These models
can then be used to compute the distribution of
aggregate losses given by equation (1) for a portfolio
of insurance risks.
in part, on what
It should be noted that
the analysis of claim
numbers depends,
is considered
to be a claim. Since many insurance policies have
deductibles, which means that small losses to the
insured are paid entirely by the insured and result in
no payment by the insurer, the term ‘claim’ usually
only refers to those events that result in a payment
by the insurer.
The computation of the aggregate claim distribu-
tion can be rather complicated. Equation (1) indi-
cates that a direct approach requires calculating
the n-fold convolutions. As an alternative, simula-
tion and numerous approximate methods have been
developed.
Approximate distributions based on the first few
lower moments is one approach; for example, gamma
distribution. Several methods for approximating spe-
cific values of the distribution function have been
developed; for example, normal power approxima-
tion, Edgeworth series, and Wilson–Hilferty trans-
form. Other numerical techniques, such as the Fast
Fourier transform, have been developed and pro-
moted. Finally, specific recursive algorithms have
been developed for certain choices of the distribu-
tion of the number of claims per unit time period
(the ‘frequency’ distribution).
Details of many approximate methods are given
in [1].
Reference
[1] Beard, R.E., Pentikainen, T. & Pesonen, E. (1984). Risk
Theory, 3rd Edition, Chapman & Hall, London.
(See also Beekman’s Convolution Formula; Claim
Size Processes; Collective Risk Theory; Com-
pound Distributions; Compound Poisson Fre-
quency Models; Continuous Parametric Distribu-
tions; Discrete Parametric Distributions; Discrete
Parametric Distributions; Discretization of Dis-
tributions; Estimation; Heckman–Meyers Algo-
rithm; Reliability Classifications; Ruin Theory;
Severity of Ruin; Sundt and Jewell Class of Dis-
tributions; Sundt’s Classes of Distributions)
HARRY H. PANJER
Approximating the
Aggregate Claims
Distribution
Introduction
The aggregate claims distribution in risk theory is
the distribution of the compound random variable
S =
N = 0
j=1 Yj N ≥ 1,
0
N
(1)
where N represents the claim frequency random
variable, and Yj is the amount (or severity) of the j th
claim. We generally assume that N is independent
of {Yj}, and that
the claim amounts Yj > 0 are
independent and identically distributed.
Typical claim frequency distributions would be
Poisson, negative binomial or binomial, or modified
versions of these. These distributions comprise the
(a, b, k) class of distributions, described more in
detail in [12].
Except for a few special cases, the distribution
function of the aggregate claims random variable is
not tractable. It is, therefore, often valuable to have
reasonably straightforward methods for approximat-
ing the probabilities. In this paper, we present some
of the methods that may be useful in practice.
We do not discuss the recursive calculation of the
distribution function, as that is covered elsewhere.
However, it is useful to note that, where the claim
amount random variable distribution is continuous,
the recursive approach is also an approximation in
so far as the continuous distribution is approximated
using a discrete distribution.
Approximating the aggregate claim distribution
using the methods discussed in this article was
crucially important historically when more accu-
rate methods such as recursions or fast Fourier
transforms were computationally infeasible. Today,
approximation methods are still useful where full
individual claim frequency or severity information
is not available; using only two or three moments
of the aggregate distribution, it is possible to apply
most of the methods described in this article. The
methods we discuss may also be used to pro-
vide quick, relatively straightforward methods for
estimating aggregate claims probabilities and as a
check on more accurate approaches.
There are two main types of approximation. The
first matches the moments of the aggregate claims
to the moments of a given distribution (for exam-
ple, normal or gamma), and then use probabili-
ties from the approximating distribution as estimates
of probabilities for the underlying aggregate claims
distribution.
The second type of approximation assumes a given
distribution for some transformation of the aggregate
claims random variable.
We will use several compound Poisson–Pareto
distributions to illustrate the application of
the
approximations. The Poisson distribution is defined
by the parameter λ = E[N]. The Pareto distribution
has a density function, mean, and kth moment
about zero
fY (y) =
E[Y k] =
(β + y)α+1 ; E[Y ] = β
α − 1
(α − 1)(α − 2) . . . (α − k)
for α > k.
k!β k
αβ α
;
(2)
The α parameter of the Pareto distribution deter-
mines the shape, with small values corresponding to
a fatter right tail. The kth moment of the distribution
exists only if α > k.
The four random variables used to illustrate the
aggregate claims approximations methods are descri-
bed below. We give the Poisson and Pareto param-
eters for each, as well as the mean µS, variance
σ 2
S , and γS, the coefficient of skewness of S, that
is, E[(S − E[S])3]/σ 3
S ], for the compound distribution
for each of the four examples.
Example 1 λ = 5, α = 4.0, β = 30; µS = 50; σ 2
1500, γS = 2.32379.
Example 2 λ = 5, α = 40.0, β = 390.0; µS = 50;
σ 2
S
Example 3 λ = 50, α = 4.0, β = 3.0; µS = 50;
σ 2
S
Example 4 λ = 50, α = 40.0, β = 39.0; µS = 50;
σ 2
S
= 1026.32, γS = 0.98706.
= 102.63, γS = 0.31214.
= 150, γS = 0.734847.
S
=
The density functions of these four random variables
were estimated using Panjer recursions [13], and are
illustrated in Figure 1. Note a significant probability
2
Approximating the Aggregate Claims Distribution
n
o
i
t
c
n
u
f
n
o
i
t
u
b
i
r
t
s
d
i
y
t
i
l
i
b
a
b
o
r
P
Example 1
Example 2
Example 3
Example 4
5
0
0
.
4
0
0
.
3
0
.
0
2
0
0
.
1
0
0
.
0
0
.
0
50
100
150
200
Aggregate claims amount
Figure 1 Probability density functions for four example random variables
mass at s = 0 for the first two cases, for which the
−5 = 0.00674. The other
probability of no claims is e
interesting feature for the purpose of approximation is
that the change in the claim frequency distribution has
a much bigger impact on the shape of the aggregate
claims distribution than changing the claim severity
distribution.
When estimating the aggregate claim distribution,
we are often most interested in the right tail of the
loss distribution – that is, the probability of very
large aggregate claims. This part of the distribution
has a significant effect on solvency risk and is key,
for example, for stop-loss and other reinsurance
calculations.
The Normal Approximation (NA)
Using the normal approximation, we estimate the
distribution of aggregate claims with the normal dis-
tribution having the same mean and variance.
This approximation can be justified by the central
limit theorem, since the sum of independent random
variables tends to a normal random variable, as the
number in the sum increases. For aggregate claims,
we are summing a random number of independent
individual claim amounts, so that the number in the
sum is itself random. The theorem still applies, and
the approximation can be used if the expected num-
ber of claims is sufficiently large. For the example
random variables, we expect a poor approximation
for Examples 1 and 2, where the expected number
of claims is only 5, and a better approximation for
Examples 3 and 4, where the expected number of
claims is 50.
In Figure 2, we show the fit of the normal distri-
bution to the four example distributions. As expected,
the approximation is very poor for low values of
E[N], but looks better for the higher values of E[N].
However, the far right tail fit is poor even for these
cases. In Table 1, we show the estimated value that
aggregate claims exceed the mean plus four standard
Table 1 Comparison of true and estimated right tail
(4 standard deviation) probabilities; Pr[S > µS + 4σS]
using the normal approximation
Example
Example 1
Example 2
Example 3
Example 4
True
probability
0.00549
0.00210
0.00157
0.00029
Normal
approximation
0.00003
0.00003
0.00003
0.00003
Approximating the Aggregate Claims Distribution
3
5
1
0
.
0
5
0
0
.
0
0
.
0
5
0
.
0
3
0
.
0
1
0
.
0
0
.
0
Actual pdf
Estimated pdf
0
50
100
Example 1
150
200
Actual pdf
Estimated pdf
5
1
0
.
0
5
0
0
.
0
0
.
0
5
0
.
0
3
0
.
0
1
0
.
0
0
.
0
Actual pdf
Estimated pdf
0
50
100
Example 2
150
200
Actual pdf
Estimated pdf
0
20
40
60
Example 3
80
100
0
20
40
60
Example 4
80
100
Figure 2 Probability density functions for four example random variables; true and normal approximation
deviations, and compare this with the ‘true’ value –
that is,
the value using Panjer recursions (this is
actually an estimate because we have discretized the
Pareto distribution). The normal distribution is sub-
stantially thinner tailed than the aggregate claims
distributions in the tail.
The Translated Gamma Approximation
The normal distribution has zero skewness, where
most aggregate claims distributions have positive
skewness. The compound Poisson and compound
negative binomial distributions are positively skewed
for any claim severity distribution. It seems natural
therefore to use a distribution with positive skewness
as an approximation. The gamma distribution was
proposed in [2] and in [8], and the translated gamma
distribution in [11]. A fuller discussion, with worked
examples is given in [5].
The gamma distribution has two parameters
and a density function (using parameterization as
in [12])
The translated gamma distribution has an identical
shape, but is assumed to be shifted by some amount
k, so that
f (x) = (x − k)a−1e
−(x−k)/θ
θ a(a)
x, a, θ > 0.
(4)
So, the translated gamma distribution has three para-
meters, (k, a, θ ) and we fit the distribution by match-
ing the first three moments of the translated gamma
distribution to the first three moments of the aggre-
gate claims distribution.
The moments of the translated gamma distribution
given by equation (4) are
Mean = aθ + k
Coefficient of Skewness >
.
(5)
Variance > aθ 2
2√
a
f (x) = xa−1e
−x/θ
θ a(a)
x, a, θ > 0.
(3)
This gives parameters for the translated gamma
example
distribution as
four
follows
for
the
4
Approximating the Aggregate Claims Distribution
distributions:
Example 1
Example 2
Example 3
Example 4
a
0.74074
4.10562
7.40741
41.05620
θ
k
45.00
16.67
15.81 −14.91
16.67
4.50
1.58 −14.91
The fit of the translated gamma distributions for the
four examples is illustrated in Figure 3; it appears
that the fit is not very good for the first example, but
looks much better for the other three. Even for the
first though, the right tail fit is not bad, especially
when compared to the normal approximation. If we
reconsider the four standard deviation tail probability
from Table 1, we find the translated gamma approx-
imation gives much better results. The numbers are
given in Table 2.
So, given three moments of the aggregate claim
distribution we can fit a translated gamma distribution
to estimate aggregate claim probabilities; the left tail
fit may be poor (as in Example 1), and the method
may give some probability for negative claims (as in
Example 2), but the right tail fit is very substantially
better than the normal approximation. This is a very
easy approximation to use in practical situations,
Table 2 Comparison of true and estimated right tail
probabilities Pr[S > E[S] + 4σS] using the translated
gamma approximation
Example
Example 1
Example 2
Example 3
Example 4
True
probability
0.00549
0.00210
0.00157
0.00029
Translated
gamma
approximation
0.00808
0.00224
0.00132
0.00030
provided that the area of the distribution of interest
is not the left tail.
Bowers Gamma Approximation
Noting that the gamma distribution was a good start-
ing point for estimating aggregate claim probabilities,
Bowers in [4] describes a method using orthogonal
polynomials to estimate the distribution function of
aggregate claims. This method differs from the pre-
vious two, in that we are not fitting a distribution to
the aggregate claims data, but rather using a func-
tional form to estimate the distribution function. The
0
3
0
.
0
0
2
0
.
0
0
1
0
.
0
0
.
0
5
0
0
.
3
0
0
.
1
0
.
0
0
0
.
Actual pdf
Estimated pdf
0
3
0
.
0
0
2
0
.
0
0
1
0
.
0
0
.
0
Actual pdf
Estimated pdf
0
50
100
150
200
0
50
100
150
200
Example 1
Actual pdf
Estimated pdf
Example 2
Actual pdf
Estimated pdf
5
0
.
0
3
0
.
0
1
0
0
.
0
.
0
0
20
40
60
Example 3
80
100
0
20
40
60
Example 4
80
100
Figure 3 Actual and translated gamma estimated probability density functions for four example random variables
Approximating the Aggregate Claims Distribution
5
first term in the Bowers formula is a gamma dis-
tribution function, and so the method is similar to
fitting a gamma distribution, without translation, to
the moments of the data, but the subsequent terms
adjust this to allow for matching higher moments of
the distribution. In the formula given in [4], the first
five moments of the aggregate claims distribution are
used; it is relatively straightforward to extend this to
even higher moments, though it is not clear that much
benefit would accrue.
Bowers’ formula is applied to a standardized ran-
dom variable, X = βS where β = E[S]/Var[S]. The
mean and variance of X then are both equal
to
E[S]2/Var[S]. If we fit a gamma (α, θ ) distribution to
the transformed random variable X, then α = E[X]
and θ = 1.
Let µk denote the kth central moment of X; note
that α = µ1 = µ2. We use the following constants:
A= µ3 − 2α
B = µ4 − 12µ3 − 3α2 + 18α
C = µ5 − 20µ4 − (10α − 120)µ3 + 6 − α2 − 144α
3!
4!
.
5!
(6)
Then the distribution function for X is estimated as
follows, where FG(x; α) represents the Gamma (α, 1)
distribution function – and is also the incomplete
gamma gamma function evaluated at x with param-
eter α.
FX(x) ≈ FG(x; α) − Ae
−x
+ xα+2
(α + 3)
+ 3xα+2
(α + 3)
xα
(α + 1)
+ Be
−x
− xα+3
(α + 4)
(α + 1)
xα
xα
− 4xα+1
(α + 2)
+ 6xα+2
(α + 3)
− 2xα+1
(α + 2)
− 3xα+1
(α + 2)
+ Ce
−x
− 4xα+3
(α + 4)
(α + 1)
+ xα+4
(α + 5)
.
(7)
Obviously,
distribution S = X/β, we have FS (s) = FX(βs).
to convert back to the original claim
If we were to ignore the third and higher moments,
and fit a gamma distribution to the first two moments,
the probability function for X would simply be
FG(x; α). The subsequent terms adjust this to match
the third, fourth, and fifth moments.
A slightly more convenient form of the formula is
F (x) ≈ FG(x; α)(1 − A + B − C) + FG(x; α + 1)
× (3A − 4B + 5C) + FG(x; α + 2)
× (−3A + 6B − 10C) + FG(x; α + 3)
× (A − 4B + 10C) + FG(x; α + 4)
× (B − 5C) + FG(x; α + 5)(C).
(8)
We cannot apply this method to all four examples, as
the kth moment of the Compound Poisson distribu-
tion exists only if the kth moment of the secondary
distribution exists. The fourth and higher moments
of the Pareto distributions with α = 4 do not exist;
it is necessary for α to be greater than k for the kth
moment of the Pareto distribution to exist. So we have
applied the approximation to Examples 2 and 4 only.
The results are shown graphically in Figure 4; we
also give the four standard deviation tail probabilities
in Table 3.
Using this method, we constrain the density to pos-
itive values only for the aggregate claims. Although
this seems realistic, the result is a poor fit in the
left side compared with the translated gamma for the
more skewed distribution of Example 2. However,
the right side fit is very similar, showing a good tail
approximation. For Example 4 the fit appears better,
and similar in right tail accuracy to the translated
gamma approximation. However, the use of two addi-
tional moments of the data seems a high price for
little benefit.
Normal Power Approximation
The normal distribution generally and unsurprisingly
offers a poor fit to skewed distributions. One method
Table 3 Comparison of true and estimated right tail
probabilities Pr[S > E[S] + 4σS] using Bower’s gamma
approximation
Example
Example 1
Example 2
Example 3
Example 4
True
probability
0.00549
0.00210
0.00157
0.00029
Bowers
approximation
n/a
0.00190
n/a
0.00030
6
Approximating the Aggregate Claims Distribution
Actual pdf
Estimated pdf
0
2
0
.
0
5
1
0
.
0
0
1
0
.
0
5
0
0
.
0
0
.
0
Actual pdf
Estimated pdf
5
0
.
0
4
0
.
0
3
0
.
0
2
0
.
0
1
0
.
0
0
.
0
0
50
100
150
200
0
20
Example 2
40
60
Example 4
80
100
Figure 4 Actual and Bower’s approximation estimated probability density functions for Example 2 and Example 4
of improving the fit whilst retaining the use of the
normal distribution function is to apply the normal
distribution to a transformation of the original ran-
dom variable, where the transformation is designed to
reduce the skewness. In [3] it is shown how this can
be taken from the Edgeworth expansion of the distri-
bution function. Let µS, σ 2
S and γS denote the mean,
variance, and coefficient of skewness of the aggregate
claims distribution respectively. Let () denote the
standard normal distribution function. Then the nor-
mal power approximation to the distribution function
is given by
FS (x) ≈
+ 1 + 6(x − µS )
γS σS
9
γ 2
S
− 3
γS
. (9)
provided the term in the square root is positive.
In [6] it is claimed that the normal power approxi-
mation does not work where the coeffient of skewness
γS > 1.0, but this is a qualitative distinction rather
than a theoretical problem – the approximation is not
very good for very highly skewed distributions.
In Figure 5, we show the normal power density
function for the four example distributions.
The right tail four standard deviation estimated
probabilities are given in Table 4.
Note that the density function is not defined at all
parts of the distribution. The normal power approx-
imation does not approximate the aggregate claims
distribution with another, it approximates the aggre-
gate claims distribution function for some values,
specifically where the square root term is positive.
The lack of a full distribution may be a disadvantage
for some analytical work, or where the left side of
the distribution is important – for example, in setting
deductibles.
Haldane’s Method
Haldane’s approximation [10] uses a similar theo-
retical approach to the normal power method – that
is, applying the normal distribution to a transforma-
tion of the original random variable. The method is
described more fully in [14], from which the follow-
ing description is taken.
The transformation is
Y =
(10)
S
h
,
µS
where h is chosen to give approximately zero skew-
ness for
for
details).
the random variable Y (see [14]
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
