便说的是，关于 ANSYS 做断裂：ANSYS 在处理2D 裂纹时，有一个命令 KSCON， 专门用来将裂纹尖端的单元转化成奇异单元。 基于 ANSYS 的双材料界面裂纹的分析 本文采用 ANSYS13.0的相互作用积分法（Interaction Integrals），分析了双材料界面 裂纹问题，通过计算得出 ANSYS 的计算结果准确可靠，为解决复杂的工程断裂问题提供一条 途径。 随着各种材料和结构断裂事故的不断出现，材料在服役过程中表现出来的断裂失效原 因逐渐引起了人们的关注。近年的研究表明，发达国家，如美、口、欧盟等在各种结构的 断裂破坏事故上的花费约占国民生产总值的6%。复合材料的内部结构形式复杂，生产工序 多，造成了复合材料内部通常会存在大量不同形式的缺陷。复合材料的服役环境一般都很 恶劣，材料内部缺陷极易引发微裂纹，从而导致复合材料发生断裂破坏。为了防范材料发 生断裂失效，延长其使用寿命，必须分析复合材料的开裂机理，了解其开裂过程，从而为 设计、制造抗破坏破坏的复合材料提供依据。 材料界面是复合材料中普遍存在的，也是断裂研究所必须面对的一个难题。目前对于 断裂参数的计算主要有直接法和间接法。直接法包括位移法和应力法，但计算精度较低。 间接法包括先求解 J 积分或能量释放率然后根据其与应力强度因子的关系，间接求解应力 强度因子但对于复合裂纹分离 I 型和 II 型应力强度因子较困难。而 ANSYS 中的相互作用积 分法有效的解决了这一问题，它可以直接求解应力强度因子，包括非均匀材料内部裂纹和 界面裂纹问题。本文即使用相互作用积分法来求解双材料界面裂纹问题，通过计算得出 ANSYS 的计算可靠，这为解决复杂工程断裂问题提供了一种便捷途径。 1 模型的建立 

图1 双材料界面裂纹几何模型 图2 双材料界面裂纹对称模型 如图1所示，一个长为2L 、宽为2W 的双材料界面上存在一个长为2a 的裂纹，板上、下 边界受均匀拉应力σ。Yuuki 和 Cho 及 Miyazaki 等采用边界元，Nagashima 等采用扩展有 限元对上述模型进行了研究。有限元计算中用到的数据如下：W=50 ;L=100 ;a/W=(0.4, 0.8) 。材料1的弹性模量 E1=2.058E5 ;材料2的弹性模量为 E2，且 E1/E2=1-500 ;材料1和 材料2的泊松比都为0.3，σ=9.8。假设板处于平面应力状态。由于模型的对称性，计算时 取模型的一半进行计算，如图2所示。图3给出了双材料界面裂纹的有限元模型。 图3 双材料界面裂纹有限元模型 

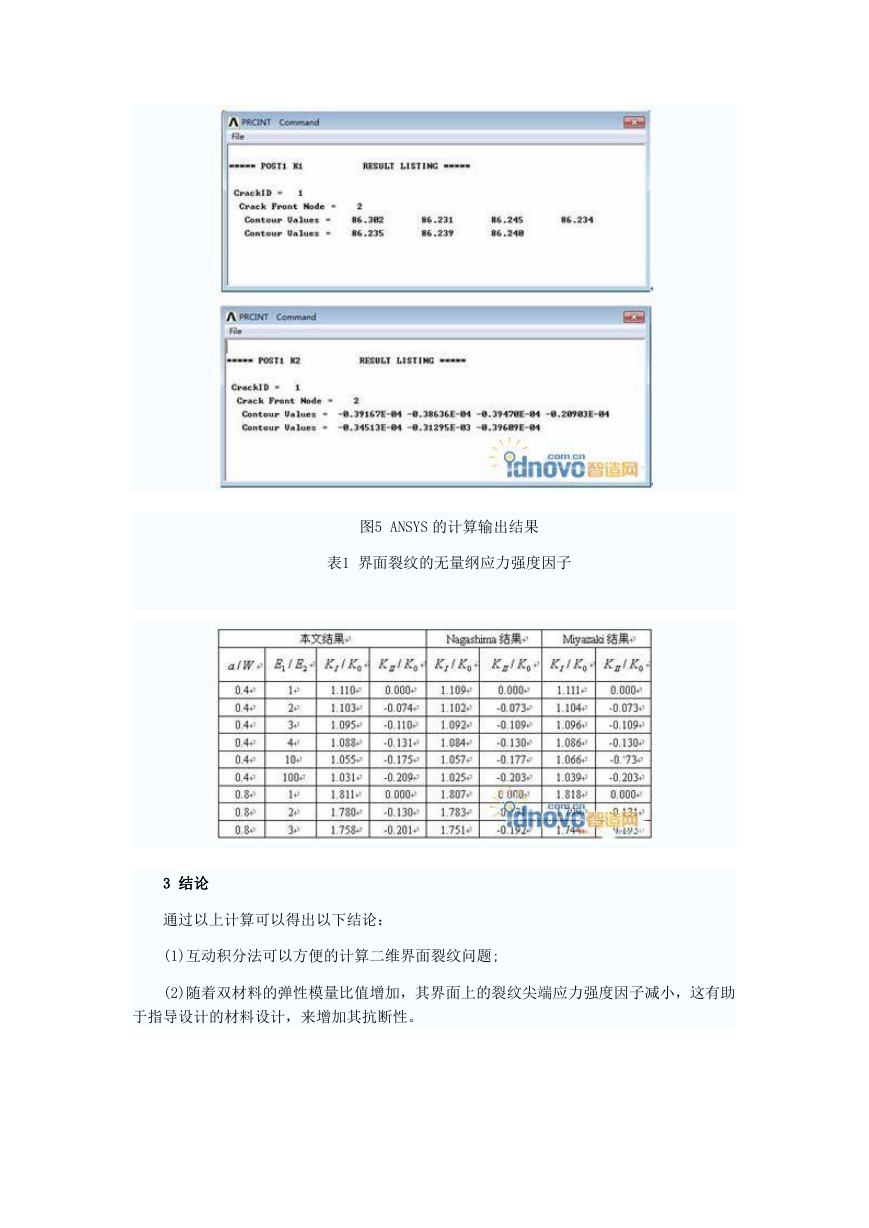
图4 裂纹尖端有限元模型 在裂纹尖端采用二维奇异单元 PLANE183模拟，其有限元网格如图4所示。计算时取7条 积分路径进行计算，并取平均值。通过 将得到的应力强度因子进行无量纲化。 2 结果与讨论 相互欣赏，相互改变，相互理解，相互进步，相互分享，相互承担，相互扶持，相互 信任，相互依靠。 图5给出了弹性模量比等于1的 ANSYS 的计算输出结果。本文的其它计算结果列于表1， 结果显示，与文献，I 型和 II 力强度因子的相对误差分别小于0.23%和1.8%。进一步观察可 以发现，随着弹性模量比值的增加，I 型应力强度因子逐渐减小，这对工程设计具有一定的 指导意义。 

图5 ANSYS 的计算输出结果 表1 界面裂纹的无量纲应力强度因子 3 结论 通过以上计算可以得出以下结论： (1)互动积分法可以方便的计算二维界面裂纹问题; (2)随着双材料的弹性模量比值增加，其界面上的裂纹尖端应力强度因子减小，这有助 于指导设计的材料设计，来增加其抗断性。