第1页 / 共19页
第2页 / 共19页
第3页 / 共19页
第4页 / 共19页
第5页 / 共19页
第6页 / 共19页
第7页 / 共19页
第8页 / 共19页
Neural Ordinary Differential Equations.pdf
1 Introduction
2 Reverse-mode automatic differentiation of ODE solutions
3 Replacing residual networks with ODEs for supervised learning
4 Continuous Normalizing Flows
4.1 Experiments with Continuous Normalizing Flows
5 A generative latent function time-series model
5.1 Time-series Latent ODE Experiments
6 Scope and Limitations
7 Related Work
8 Conclusion
9 Acknowledgements
A Proof of the Instantaneous Change of Variables Theorem
A.1 Special Cases
A.2 Connection to Fokker-Planck and Liouville PDEs
B A Modern Proof of the Adjoint Method
B.1 Continuous Backpropagation
B.2 Gradients wrt. and t
C Full Adjoint sensitivities algorithm
D Autograd Implementation
E Algorithm for training the latent ODE model
F Extra Figures
Neural Ordinary Differential Equations
Ricky T. Q. Chen*, Yulia Rubanova*, Jesse Bettencourt*, David Duvenaud
{rtqichen, rubanova, jessebett, duvenaud}@cs.toronto.edu
University of Toronto, Vector Institute
9
1
0
2
n
a
J
5
1
]
G
L
.
s
c
[
4
v
6
6
3
7
0
.
6
0
8
1
:
v
i
X
r
a
Abstract
We introduce a new family of deep neural network models. Instead of specifying a
discrete sequence of hidden layers, we parameterize the derivative of the hidden
state using a neural network. The output of the network is computed using a black-
box differential equation solver. These continuous-depth models have constant
memory cost, adapt their evaluation strategy to each input, and can explicitly trade
numerical precision for speed. We demonstrate these properties in continuous-depth
residual networks and continuous-time latent variable models. We also construct
continuous normalizing flows, a generative model that can train by maximum
likelihood, without partitioning or ordering the data dimensions. For training, we
show how to scalably backpropagate through any ODE solver, without access to its
internal operations. This allows end-to-end training of ODEs within larger models.
1
Introduction
Models such as residual networks, recurrent neural
network decoders, and normalizing flows build com-
plicated transformations by composing a sequence of
transformations to a hidden state:
ht+1 = ht + f (ht, θt)
(1)
where t ∈ {0 . . . T} and ht ∈ RD. These iterative
updates can be seen as an Euler discretization of a
continuous transformation (Lu et al., 2017; Haber
and Ruthotto, 2017; Ruthotto and Haber, 2018).
What happens as we add more layers and take smaller
steps? In the limit, we parameterize the continuous
dynamics of hidden units using an ordinary differen-
tial equation (ODE) specified by a neural network:
dh(t)
dt
= f (h(t), t, θ)
(2)
Residual Network
ODE Network
Figure 1: Left: A Residual network defines a
discrete sequence of finite transformations.
Right: A ODE network defines a vector
field, which continuously transforms the state.
Both: Circles represent evaluation locations.
Starting from the input layer h(0), we can define the output layer h(T ) to be the solution to this
ODE initial value problem at some time T . This value can be computed by a black-box differential
equation solver, which evaluates the hidden unit dynamics f wherever necessary to determine the
solution with the desired accuracy. Figure 1 contrasts these two approaches.
Defining and evaluating models using ODE solvers has several benefits:
Memory efficiency In Section 2, we show how to compute gradients of a scalar-valued loss with
respect to all inputs of any ODE solver, without backpropagating through the operations of the solver.
Not storing any intermediate quantities of the forward pass allows us to train our models with constant
memory cost as a function of depth, a major bottleneck of training deep models.
32nd Conference on Neural Information Processing Systems (NeurIPS 2018), Montréal, Canada.
505Input/Hidden/Output012345Depth505Input/Hidden/Output012345Depth
Adaptive computation Euler’s method is perhaps the simplest method for solving ODEs. There
have since been more than 120 years of development of efficient and accurate ODE solvers (Runge,
1895; Kutta, 1901; Hairer et al., 1987). Modern ODE solvers provide guarantees about the growth
of approximation error, monitor the level of error, and adapt their evaluation strategy on the fly to
achieve the requested level of accuracy. This allows the cost of evaluating a model to scale with
problem complexity. After training, accuracy can be reduced for real-time or low-power applications.
Parameter efficiency When the hidden unit dynamics are parameterized as a continuous function
of time, the parameters of nearby “layers” are automatically tied together. In Section 3, we show that
this reduces the number of parameters required on a supervised learning task.
Scalable and invertible normalizing flows An unexpected side-benefit of continuous transforma-
tions is that the change of variables formula becomes easier to compute. In Section 4, we derive
this result and use it to construct a new class of invertible density models that avoids the single-unit
bottleneck of normalizing flows, and can be trained directly by maximum likelihood.
Continuous time-series models Unlike recurrent neural networks, which require discretizing
observation and emission intervals, continuously-defined dynamics can naturally incorporate data
which arrives at arbitrary times. In Section 5, we construct and demonstrate such a model.
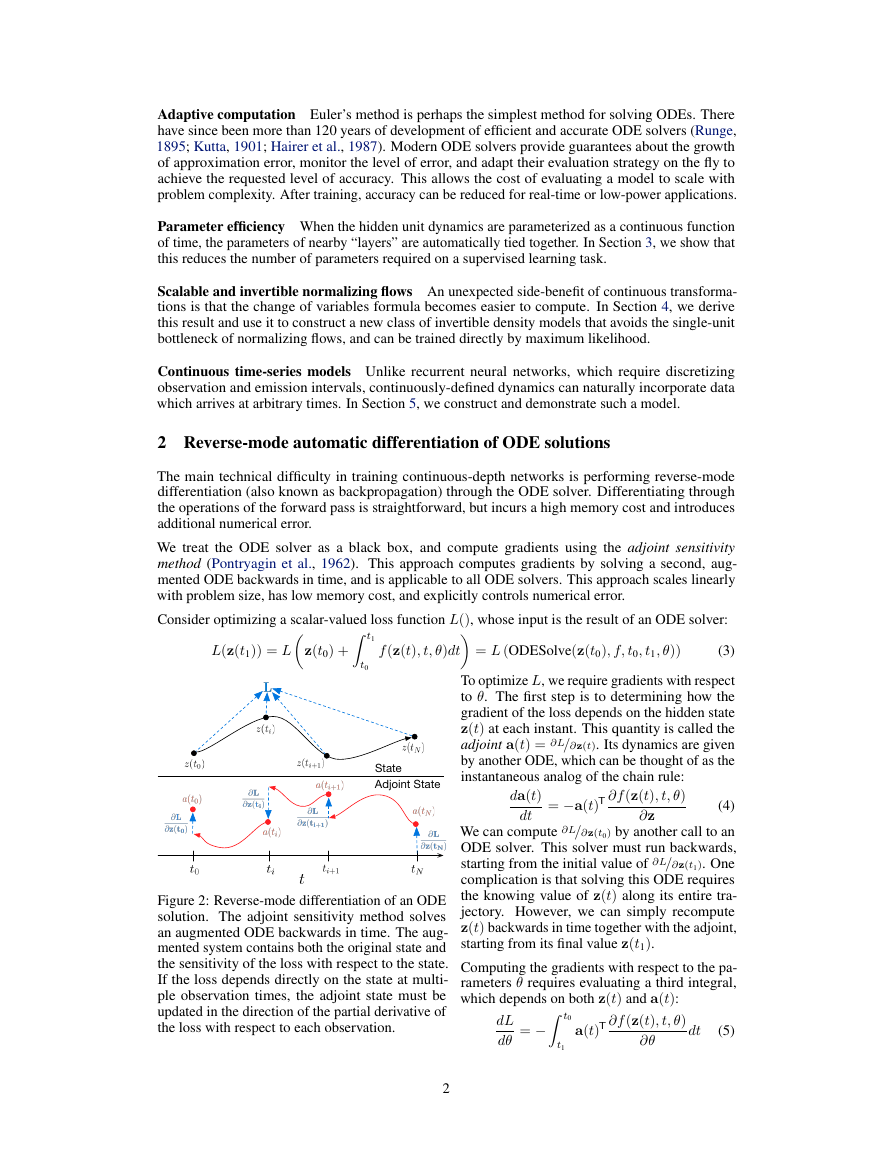
2 Reverse-mode automatic differentiation of ODE solutions
t1
The main technical difficulty in training continuous-depth networks is performing reverse-mode
differentiation (also known as backpropagation) through the ODE solver. Differentiating through
the operations of the forward pass is straightforward, but incurs a high memory cost and introduces
additional numerical error.
We treat the ODE solver as a black box, and compute gradients using the adjoint sensitivity
method (Pontryagin et al., 1962). This approach computes gradients by solving a second, aug-
mented ODE backwards in time, and is applicable to all ODE solvers. This approach scales linearly
with problem size, has low memory cost, and explicitly controls numerical error.
Consider optimizing a scalar-valued loss function L(), whose input is the result of an ODE solver:
L(z(t1)) = L
z(t0) +
f (z(t), t, θ)dt
= L (ODESolve(z(t0), f, t0, t1, θ))
(3)
t0
To optimize L, we require gradients with respect
to θ. The first step is to determining how the
gradient of the loss depends on the hidden state
z(t) at each instant. This quantity is called the
adjoint a(t) = ∂L/∂z(t). Its dynamics are given
by another ODE, which can be thought of as the
instantaneous analog of the chain rule:
∂z
da(t)
dt
= −a(t)T ∂f (z(t), t, θ)
(4)
We can compute ∂L/∂z(t0) by another call to an
ODE solver. This solver must run backwards,
starting from the initial value of ∂L/∂z(t1). One
complication is that solving this ODE requires
the knowing value of z(t) along its entire tra-
jectory. However, we can simply recompute
z(t) backwards in time together with the adjoint,
starting from its final value z(t1).
Computing the gradients with respect to the pa-
rameters θ requires evaluating a third integral,
which depends on both z(t) and a(t):
a(t)T ∂f (z(t), t, θ)
t0
dt
(5)
dL
dθ
= −
t1
∂θ
Figure 2: Reverse-mode differentiation of an ODE
solution. The adjoint sensitivity method solves
an augmented ODE backwards in time. The aug-
mented system contains both the original state and
the sensitivity of the loss with respect to the state.
If the loss depends directly on the state at multi-
ple observation times, the adjoint state must be
updated in the direction of the partial derivative of
the loss with respect to each observation.
2
Adjoint StateState
The vector-Jacobian products a(t)T ∂f
∂θ in (4) and (5) can be efficiently evaluated by
automatic differentiation, at a time cost similar to that of evaluating f. All integrals for solving z, a
and ∂L
∂θ can be computed in a single call to an ODE solver, which concatenates the original state, the
adjoint, and the other partial derivatives into a single vector. Algorithm 1 shows how to construct the
necessary dynamics, and call an ODE solver to compute all gradients at once.
∂z and a(t)T ∂f
Algorithm 1 Reverse-mode derivative of an ODE initial value problem
Input: dynamics parameters θ, start time t0, stop time t1, final state z(t1), loss gradient ∂L/∂z(t1)
Define initial augmented state
Define dynamics on augmented state
Compute vector-Jacobian products
Solve reverse-time ODE
Return gradients
∂z(t1) , 0|θ|]
s0 = [z(t1), ∂L
def aug_dynamics([z(t), a(t),·], t, θ):
[z(t0),
return [f (z(t), t, θ),−a(t)T ∂f
∂z ,−a(t)T ∂f
∂θ ]
return
∂L
∂z(t0) , ∂L
∂z(t0) , ∂L
∂L
∂θ
∂θ ] = ODESolve(s0, aug_dynamics, t1, t0, θ)
Most ODE solvers have the option to output the state z(t) at multiple times. When the loss depends
on these intermediate states, the reverse-mode derivative must be broken into a sequence of separate
solves, one between each consecutive pair of output times (Figure 2). At each observation, the adjoint
must be adjusted in the direction of the corresponding partial derivative ∂L/∂z(ti).
The results above extend those of Stapor et al. (2018, section 2.4.2). An extended version of
Algorithm 1 including derivatives w.r.t. t0 and t1 can be found in Appendix C. Detailed derivations
are provided in Appendix B. Appendix D provides Python code which computes all derivatives for
scipy.integrate.odeint by extending the autograd automatic differentiation package. This
code also supports all higher-order derivatives. We have since released a PyTorch (Paszke et al.,
2017) implementation, including GPU-based implementations of several standard ODE solvers at
github.com/rtqichen/torchdiffeq.
3 Replacing residual networks with ODEs for supervised learning
In this section, we experimentally investigate the training of neural ODEs for supervised learning.
Software To solve ODE initial value problems numerically, we use the implicit Adams method
implemented in LSODE and VODE and interfaced through the scipy.integrate package. Being
an implicit method, it has better guarantees than explicit methods such as Runge-Kutta but requires
solving a nonlinear optimization problem at every step. This setup makes direct backpropagation
through the integrator difficult. We implement the adjoint sensitivity method in Python’s autograd
framework (Maclaurin et al., 2015). For the experiments in this section, we evaluated the hidden
state dynamics and their derivatives on the GPU using Tensorflow, which were then called from the
Fortran ODE solvers, which were called from Python autograd code.
Table 1: Performance on MNIST. †From LeCun
et al. (1998).
Model Architectures We experiment with a
small residual network which downsamples the
input twice then applies 6 standard residual
blocks He et al. (2016b), which are replaced
by an ODESolve module in the ODE-Net vari-
ant. We also test a network with the same archi-
O(L)
O( ˜L)
tecture but where gradients are backpropagated
O( ˜L)
directly through a Runge-Kutta integrator, re-
ferred to as RK-Net. Table 1 shows test error, number of parameters, and memory cost. L denotes
the number of layers in the ResNet, and ˜L is the number of function evaluations that the ODE solver
requests in a single forward pass, which can be interpreted as an implicit number of layers.
We find that ODE-Nets and RK-Nets can achieve around the same performance as the ResNet, while
using fewer parameters. For reference, a neural net with a single hidden layer of 300 units has around
the same number of parameters as the ODE-Net and RK-Net architecture that we tested.
# Params Memory
0.24 M
0.60 M
0.22 M
0.22 M
1-Layer MLP†
ResNet
RK-Net
ODE-Net
1.60%
0.41%
0.47%
0.42%
O(L)
O( ˜L)
O(1)
Test Error
-
Time
-
3
Error Control in ODE-Nets ODE solvers can approximately ensure that the output is within a
given tolerance of the true solution. Changing this tolerance changes the behavior of the network.
We first verify that error can indeed be controlled in Figure 3a. The time spent by the forward call is
proportional to the number of function evaluations (Figure 3b), so tuning the tolerance gives us a
trade-off between accuracy and computational cost. One could train with high accuracy, but switch to
a lower accuracy at test time.
Figure 3: Statistics of a trained ODE-Net. (NFE = number of function evaluations.)
Figure 3c) shows a surprising result: the number of evaluations in the backward pass is roughly
half of the forward pass. This suggests that the adjoint sensitivity method is not only more memory
efficient, but also more computationally efficient than directly backpropagating through the integrator,
because the latter approach will need to backprop through each function evaluation in the forward
pass.
Network Depth It’s not clear how to define the ‘depth‘ of an ODE solution. A related quantity is
the number of evaluations of the hidden state dynamics required, a detail delegated to the ODE solver
and dependent on the initial state or input. Figure 3d shows that he number of function evaluations
increases throughout training, presumably adapting to increasing complexity of the model.
4 Continuous Normalizing Flows
The discretized equation (1) also appears in normalizing flows (Rezende and Mohamed, 2015) and
the NICE framework (Dinh et al., 2014). These methods use the change of variables theorem to
compute exact changes in probability if samples are transformed through a bijective function f:
z1 = f (z0) =⇒ log p(z1) = log p(z0) − log
An example is the planar normalizing flow (Rezende and Mohamed, 2015):
z(t + 1) = z(t) + uh(wTz(t) + b),
log p(z(t + 1)) = log p(z(t)) − log
1 + uT ∂h
∂z
(6)
(7)
det
∂f
∂z0
Generally, the main bottleneck to using the change of variables formula is computing of the deter-
minant of the Jacobian ∂f/∂z, which has a cubic cost in either the dimension of z, or the number
of hidden units. Recent work explores the tradeoff between the expressiveness of normalizing flow
layers and computational cost (Kingma et al., 2016; Tomczak and Welling, 2016; Berg et al., 2018).
Surprisingly, moving from a discrete set of layers to a continuous transformation simplifies the
computation of the change in normalizing constant:
Theorem 1 (Instantaneous Change of Variables). Let z(t) be a finite continuous random variable
with probability p(z(t)) dependent on time. Let dz
dt = f (z(t), t) be a differential equation describing
a continuous-in-time transformation of z(t). Assuming that f is uniformly Lipschitz continuous in z
and continuous in t, then the change in log probability also follows a differential equation,
df
∂ log p(z(t))
∂t
= −tr
dz(t)
(8)
Proof in Appendix A. Instead of the log determinant in (6), we now only require a trace operation.
Also unlike standard finite flows, the differential equation f does not need to be bijective, since if
uniqueness is satisfied, then the entire transformation is automatically bijective.
4
As an example application of the instantaneous change of variables, we can examine the continuous
analog of the planar flow, and its change in normalization constant:
dz(t)
dt
= uh(wTz(t) + b),
∂ log p(z(t))
∂t
= −uT ∂h
∂z(t)
(9)
Given an initial distribution p(z(0)), we can sample from p(z(t)) and evaluate its density by solving
this combined ODE.
is, which implies tr(
Using multiple hidden units with linear cost While det is not a linear function, the trace function
n tr(Jn). Thus if our dynamics is given by a sum of functions then
the differential equation for the log density is also a sum:
n Jn) =
M
dz(t)
=
dt
n=1
fn(z(t)),
d log p(z(t))
dt
=
(10)
∂fn
∂z
M
n=1
tr
This means we can cheaply evaluate flow models having many hidden units, with a cost only linear in
the number of hidden units M. Evaluating such ‘wide’ flow layers using standard normalizing flows
costs O(M 3), meaning that standard NF architectures use many layers of only a single hidden unit.
Time-dependent dynamics We can specify the parameters of a flow as a function of t, making the
differential equation f (z(t), t) change with t. This is parameterization is a kind of hypernetwork (Ha
et al., 2016). We also introduce a gating mechanism for each hidden unit, dz
n σn(t)fn(z)
where σn(t) ∈ (0, 1) is a neural network that learns when the dynamic fn(z) should be applied. We
call these models continuous normalizing flows (CNF).
dt =
4.1 Experiments with Continuous Normalizing Flows
We first compare continuous and discrete planar flows at learning to sample from a known distribution.
We show that a planar CNF with M hidden units can be at least as expressive as a planar NF with
K = M layers, and sometimes much more expressive.
Density matching We configure the CNF as described above, and train for 10,000 iterations
using Adam (Kingma and Ba, 2014). In contrast, the NF is trained for 500,000 iterations using
RMSprop (Hinton et al., 2012), as suggested by Rezende and Mohamed (2015). For this task, we
minimize KL (q(x)p(x)) as the loss function where q is the flow model and the target density p(·)
can be evaluated. Figure 4 shows that CNF generally achieves lower loss.
Maximum Likelihood Training A useful property of continuous-time normalizing flows is that
we can compute the reverse transformation for about the same cost as the forward pass, which cannot
be said for normalizing flows. This lets us train the flow on a density estimation task by performing
K=2
K=8
K=32
M=2
M=8 M=32
1
2
3
(a) Target
(b) NF
(c) CNF
(d) Loss vs. K/M
Figure 4: Comparison of normalizing flows versus continuous normalizing flows. The model capacity
of normalizing flows is determined by their depth (K), while continuous normalizing flows can also
increase capacity by increasing width (M), making them easier to train.
5
102030CNFNF102030CNFNF102030CNFNF
5% 20% 40% 60% 80% 100%
5% 20% 40% 60% 80% 100%
y
t
i
s
n
e
D
s
e
l
p
m
a
S
F
N
y
t
i
s
n
e
D
s
e
l
p
m
a
S
F
N
Target
Target
(a) Two Circles
(b) Two Moons
Figure 5: Visualizing the transformation from noise to data. Continuous-time normalizing flows
are reversible, so we can train on a density estimation task and still be able to sample from the learned
density efficiently.
maximum likelihood estimation, which maximizes E
p(x)[log q(x)] where q(·) is computed using
the appropriate change of variables theorem, then afterwards reverse the CNF to generate random
samples from q(x).
For this task, we use 64 hidden units for CNF, and 64 stacked one-hidden-unit layers for NF. Figure 5
shows the learned dynamics. Instead of showing the initial Gaussian distribution, we display the
transformed distribution after a small amount of time which shows the locations of the initial planar
flows. Interestingly, to fit the Two Circles distribution, the CNF rotates the planar flows so that
the particles can be evenly spread into circles. While the CNF transformations are smooth and
interpretable, we find that NF transformations are very unintuitive and this model has difficulty fitting
the two moons dataset in Figure 5b.
5 A generative latent function time-series model
Applying neural networks to irregularly-sampled data such as medical records, network traffic, or
neural spiking data is difficult. Typically, observations are put into bins of fixed duration, and the
latent dynamics are discretized in the same way. This leads to difficulties with missing data and ill-
defined latent variables. Missing data can be addressed using generative time-series models (Álvarez
and Lawrence, 2011; Futoma et al., 2017; Mei and Eisner, 2017; Soleimani et al., 2017a) or data
imputation (Che et al., 2018). Another approach concatenates time-stamp information to the input of
an RNN (Choi et al., 2016; Lipton et al., 2016; Du et al., 2016; Li, 2017).
We present a continuous-time, generative approach to modeling time series. Our model represents
each time series by a latent trajectory. Each trajectory is determined from a local initial state, zt0, and
a global set of latent dynamics shared across all time series. Given observation times t0, t1, . . . , tN
and an initial state zt0, an ODE solver produces zt1 , . . . , ztN , which describe the latent state at each
observation.We define this generative model formally through a sampling procedure:
zt0 ∼ p(zt0)
zt1 , zt2 , . . . , ztN = ODESolve(zt0, f, θf , t0, . . . , tN )
each xti ∼ p(x|zti, θx)
(11)
(12)
(13)
Function f is a time-invariant function that takes the value z at the current time step and outputs the
gradient: ∂z(t)/∂t = f (z(t), θf ). We parametrize this function using a neural net. Because f is time-
invariant, given any latent state z(t), the entire latent trajectory is uniquely defined. Extrapolating
this latent trajectory lets us make predictions arbitrarily far forwards or backwards in time.
Training and Prediction We can train this latent-variable model as a variational autoen-
coder (Kingma and Welling, 2014; Rezende et al., 2014), with sequence-valued observations. Our
recognition net is an RNN, which consumes the data sequentially backwards in time, and out-
puts qφ(z0|x1, x2, . . . , xN ). A detailed algorithm can be found in Appendix E. Using ODEs as a
generative model allows us to make predictions for arbitrary time points t1...tM on a continuous
timeline.
6
Figure 6: Computation graph of the latent ODE model.
Poisson Process likelihoods The fact that an observation oc-
curred often tells us something about the latent state. For ex-
ample, a patient may be more likely to take a medical test if
they are sick. The rate of events can be parameterized by a
function of the latent state: p(event at time t| z(t)) = λ(z(t)).
Given this rate function, the likelihood of a set of indepen-
dent observation times in the interval [tstart, tend] is given by an
inhomogeneous Poisson process (Palm, 1943):
)
t
(
λ
t
N
i=1
tend
tstart
Figure 7: Fitting a latent ODE dy-
namics model with a Poisson pro-
cess likelihood. Dots show event
times. The line is the learned inten-
sity λ(t) of the Poisson process.
λ(z(t))dt
log λ(z(ti)) −
log p(t1 . . . tN| tstart, tend) =
We can parameterize λ(·) using another neural network. Con-
veniently, we can evaluate both the latent trajectory and the
Poisson process likelihood together in a single call to an ODE solver. Figure 7 shows the event rate
learned by such a model on a toy dataset.
A Poisson process likelihood on observation times can be combined with a data likelihood to jointly
model all observations and the times at which they were made.
5.1 Time-series Latent ODE Experiments
We investigate the ability of the latent ODE model to fit and extrapolate time series. The recognition
network is an RNN with 25 hidden units. We use a 4-dimensional latent space. We parameterize the
dynamics function f with a one-hidden-layer network with 20 hidden units. The decoder computing
p(xti|zti) is another neural network with one hidden layer with 20 hidden units. Our baseline was a
recurrent neural net with 25 hidden units trained to minimize negative Gaussian log-likelihood. We
trained a second version of this RNN whose inputs were concatenated with the time difference to the
next observation to aid RNN with irregular observations.
Bi-directional spiral dataset We generated a
dataset of 1000 2-dimensional spirals, each start-
ing at a different point, sampled at 100 equally-
spaced timesteps. The dataset contains two
types of spirals: half are clockwise while the
other half counter-clockwise. To make the task
more realistic, we add gaussian noise to the observations.
# Observations
RNN
Latent ODE
Table 2: Predictive RMSE on test set
30/100
0.3937
0.1642
50/100
0.3202
0.1502
100/100
0.1813
0.1346
Time series with irregular time points To generate irregular timestamps, we randomly sample
points from each trajectory without replacement (n = {30, 50, 100}). We report predictive root-
mean-squared error (RMSE) on 100 time points extending beyond those that were used for training.
Table 2 shows that the latent ODE has substantially lower predictive RMSE.
Figure 8 shows examples of spiral reconstructions with 30 sub-sampled points. Reconstructions from
the latent ODE were obtained by sampling from the posterior over latent trajectories and decoding it
7
µ zt0zt1RNN encoderLatent spaceData space~q(zt0|xt0...xtN)ht0ht1htNODESolve(zt0,f,✓f,t0,...,tM)ztM…ztNztN+1ObservedUnobservedx(t)t0t1tNTimetN+1tMPredictionExtrapolationt0t1tNtN+1tMˆx(t)
Figure 9: Data-space trajectories decoded from varying one dimension of zt0. Color indicates
progression through time, starting at purple and ending at red. Note that the trajectories on the left
are counter-clockwise, while the trajectories on the right are clockwise.
to data-space. Examples with varying number of time points are shown in Appendix F. We observed
that reconstructions and extrapolations are consistent with the ground truth regardless of number of
observed points and despite the noise.
Latent space interpolation Figure 8c shows
latent trajectories projected onto the first two
dimensions of the latent space. The trajecto-
ries form two separate clusters of trajectories,
one decoding to clockwise spirals, the other to
counter-clockwise. Figure 9 shows that the la-
tent trajectories change smoothly as a function
of the initial point z(t0), switching from a clock-
wise to a counter-clockwise spiral.
6 Scope and Limitations
Minibatching The use of mini-batches is less
straightforward than for standard neural net-
works. One can still batch together evaluations
through the ODE solver by concatenating the
states of each batch element together, creating a
combined ODE with dimension D×K. In some
cases, controlling error on all batch elements to-
gether might require evaluating the combined
system K times more often than if each system
was solved individually. However, in practice
the number of evaluations did not increase sub-
stantially when using minibatches.
Uniqueness When do continuous dynamics
have a unique solution? Picard’s existence the-
orem (Coddington and Levinson, 1955) states
that the solution to an initial value problem ex-
ists and is unique if the differential equation is
uniformly Lipschitz continuous in z and contin-
uous in t. This theorem holds for our model if
the neural network has finite weights and uses
Lipshitz nonlinearities, such as tanh or relu.
(a) Recurrent Neural Network
(b) Latent Neural Ordinary Differential Equation
(c) Latent Trajectories
Figure 8: (a): Reconstruction and extrapolation
of spirals with irregular time points by a recurrent
neural network. (b): Reconstructions and extrapo-
lations by a latent neural ODE. Blue curve shows
model prediction. Red shows extrapolation. (c) A
projection of inferred 4-dimensional latent ODE
trajectories onto their first two dimensions. Color
indicates the direction of the corresponding trajec-
tory. The model has learned latent dynamics which
distinguishes the two directions.
Setting tolerances Our framework allows the user to trade off speed for precision, but requires
the user to choose an error tolerance on both the forward and reverse passes during training. For
sequence modeling, the default value of 1.5e-8 was used. In the classification and density estimation
experiments, we were able to reduce the tolerance to 1e-3 and 1e-5, respectively, without degrading
performance.
Reconstructing forward trajectories Reconstructing the state trajectory by running the dynamics
backwards can introduce extra numerical error if the reconstructed trajectory diverges from the
original. This problem can be addressed by checkpointing: storing intermediate values of z on the
8
Ground TruthObservationPredictionExtrapolation
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
