Signal Detection And Estimation - Solution Manual.pdf-资料库

Chapter 1 Probability Concepts 1.1 The given sets are: A = {1,2,3,4} B = {0,1,2,3,4,5,6,7,8} C = {x | x real and 1≤ x <3} D = {2,4,7} E = {4,7,8,9,10}. We observe that: 1.2 By inspection, A is finite and countable. B is finite and countable. C is infinite and uncountable. D is finite and countable. E is finite and countable. (a) BA I = A = {1,2,3,4}. (b) EDBA UUU = {1,2,3,4,5,6,7,8,9,10}. (c) ( DEB U ) I = D = {2,4,7}. (d) EB − = {1,2,3,5,6}. (e) EDBA III ={4}. 1.3 The universal set is U = {0,1,2,3,4,5,6,7,8,9,10,11,12}. The subsets are A = {0,1,4,6,7,9}, B = {2,4,6,8,10,12} and C = {1,3,5,7,9,11}. By inspection, (a) BA I = {4,6}. (b) ( BA U ) CI = CA I = {1,7,9}. 1

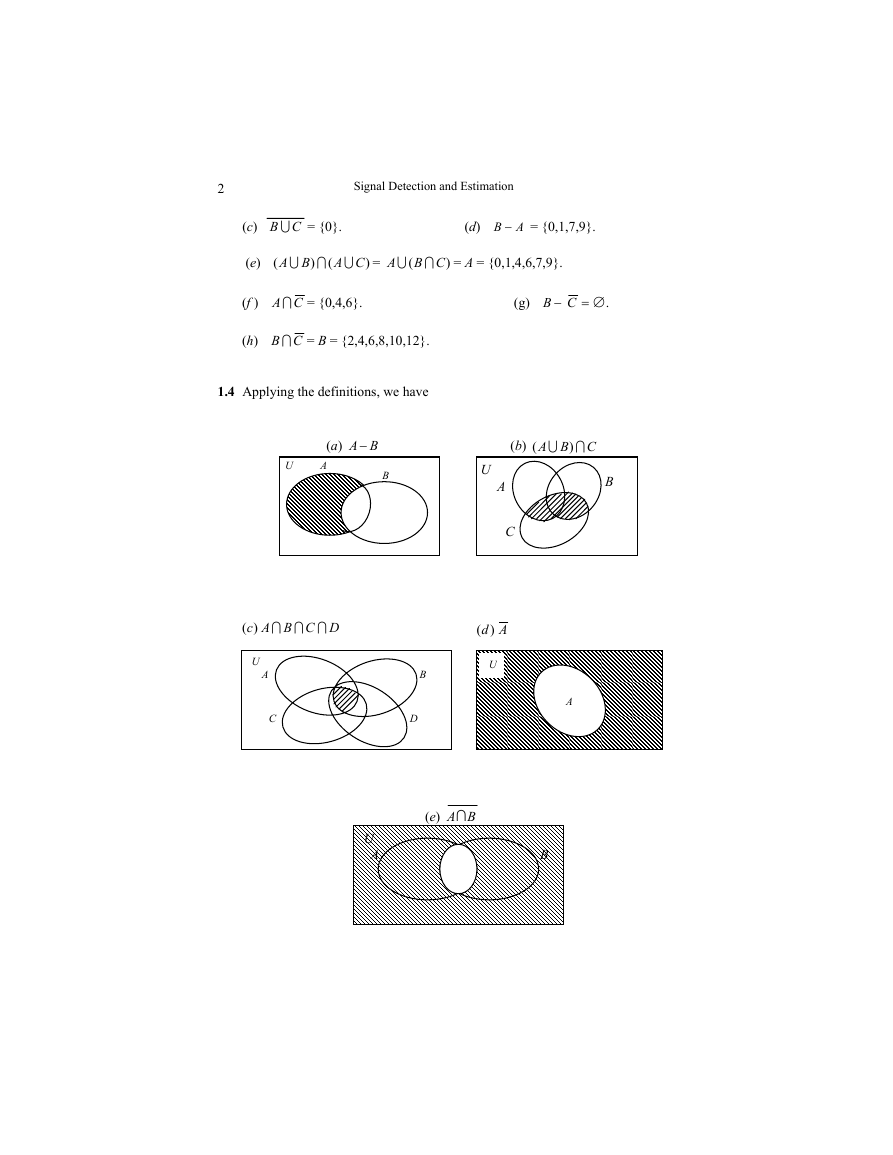
2 Signal Detection and Estimation (c) CB U = {0}. (d) AB − = {0,1,7,9}. (e) ( BA U ) ( CA U ) I = A ( CB I ) U = A = {0,1,4,6,7,9}. (f ) CA I = {0,4,6}. (g) −B =C ∅. (h) CB I = B = {2,4,6,8,10,12}. 1.4 Applying the definitions, we have (a) BA − U A B III )( DCBAc U A B C D B (b) ( CBA U ) I U A C Ad)( U A (e) A∩B U A B

Probability Concepts 1.5 This is easily verified by Venn diagrams. Hence, we have BA ⊂ and CB ⊂ , then B A C B U B C CA ⊂ A 3 1.6 By inspection, B and C are mutually exclusive. 1.7 Let R, W and B denote red ball drawn, white ball drawn and blue ball drawn, respectively 10R , 3W, 7B (a) =RP ( ) (b) =WP ( ) balls red of Number Total of balls number 3 20 15.0 = . 10 73 ++ = 10 = 1 2 = 5.0 . = 35.0 . (c) (e) ) =BP ( 7 20 =WRP U ( ) 3 10 + 20 = 13 20 = 65.0 . (d) RP ( 1) −= RP ( ) = 1 2 = 5.0 . B1 ≡ first ball drawn is blue. W2 ≡ 2nd ball drawn is white. R3 ≡ 3rd ball drawn is red. 1.8 Let and hence, (a) The ball is replaced before the next draw ⇒ the events are independent 1 RWBP ( I I 2 ) 3 | 3 1 1 2 2 | ) ( ) ) = 1 RPWPBP= ( 210 8000 WBRPBWPBP ( ( 7 20 () ( ) 1 3 10 20 20 02625 .0 = = = I 3 ) 2

4 Signal Detection and Estimation (b) Since the ball is not replaced, the sample size changes and thus, the events are dependent. Hence, RWBP ( 1 I 2 I 1.9 ) = 3 = | 2 1 ) ( WBRPBWPBP ( 7 20 ( 10 18 ) 1 3 19 0307 .0 = I 1 3 | ) 2 10R , 3W B1 7B 2R , 6W B2 1B Let R1 and R2 denote draw a red ball from box B1 and B2 respectively, and let W1 and W2 denote also draw a white ball from B1 and B2. = RRPRP ( 1 ( ) 2 1 | ) = RPRP ( ( ) 1 2 ) since the events are (a) ) 2 independent. Hence, RP ( 1 R I RP ( 1 =R 2 ) I 10 20 2 9 = 1 9 = .0 111 . (b) Similarly, WWP ( 2 1 I ) = WPWP ( 2 ( ) 1 ) = 3 20 6 9 = 1.0 (c) Since we can have a different color from each box separately, then BWP ( I ) = BWP ( 1 I ) + 2 BWP ( 1 2 I ) = 3 20 1 9 + 6 9 7 20 = 25.0 . 1.10 Let B1 and B2 denote Box 1 and 2 respectively. Let B denote drawing a black ball and W a white ball. Then , B1 4W , 2B B2 3W , 5B

Probability Concepts 5 Let B2 be the larger box, then P(B2) = 2P(B1). Since BP ( ) + BP ( 1 2 1) = , we obtain BP ( 1 ) = 1 3 and BP ( 2 ) = 2 3 . (a) P(1B | B2) = = .0 625 . 5 8 2 6 (b) P(1B | B1) = (c) This is the total probability of drawing a black ball. Hence 3333 .0 = . BP )1( = = 2 BPBBP |1( 2 5 8 3 ( 1 3 ) 2 6 + = ) 2 .0 5278 . + BPBBP |1( 1 ( ) 1 ) (d) Similarly, the probability of drawing a white ball is BPBWPWP )1( = ( | ) + BPBWP 1( 1 ( ) 1 | = 1( 3 8 ) 1 3 2 4 6 2 3 + 2 .0 = 4722 . ) 1.11 In four tosses:__ __ __ __, we have three 1s and one is not 1. For example 111 . Hence, the probability is 1 1 6 1 6 1 6 5 6 =   1 6    3 5 6 but we have    4 3    ways of obtaining this. Therefore, the probability of obtaining 3 ones in 4 tosses is !4 !1!3    1 6    3 5 6 = .0 01543 . 1.12 Let R, W and G represent drawing a red ball, a white ball, and a green ball respectively. Note that the probability of selecting Urn A is P(Urn A) = 0.6, Urn B is P(Urn B) = 0.2 and Urn C is P(Urn C) = 0.2 since P(Urn A)+P(Urn B)+P(Urn C) =1. (a) (P 1W | Urn B) = WP 1( P Urn I B ) (Urn B ) = 30 100 = 3.0 . (b) (P 1G | Urn B) = (c) P(Urn C | R) = P . 40 4.0 = 100 I RC (Urn RP ) ( ) . Also,

6 Signal Detection and Estimation P(R | Urn C) = P (Urn P I RC C (Urn ) ) ⇒ P (Urn RC | ) = RP ( | Urn PC ) RP ) ( (Urn C ) . We need to determine the total probability of drawing a red ball, which is RP ( ) = = Thus, P (Urn Urn ) | ( 6.0 RP ( 30 100 =RC | ) (Urn ( 2.0 A ) ) + PA ) 30 100 + )2.0()4.0( | RP ( + 40 ( 2.0 100 25.0 . = 32.0 PB ) (Urn B ) + RP ( | Urn PC ) (Urn C ) Urn ) = 32.0 1.13 In drawing k balls, the probability that the sample drawn does not contain a particular ball in the event Ei, i = 0, 1,2, … , 9, is EP ( ) i =   EEP ( i j ) M 9 10 =   k    8 10 k    (a) P(A) = P(neither ball 0 nor ball1) = P(E0E1) = 8 10 (b) P(B) = P( ball 1 does not appear but ball 2 does) k k . = EP ( 1 ) − EEP ( 1 2 ) = k 9 10 k − k 8 10 k = 9 k k 8 − k 10 . − k 7 10 k = 8 k k 7 − k 10 . (c) P(AB) = 0 EEEP ( 1 2 ) = EEP ( 1 0 ) − EEEP ( 1 0 (d) BAP ( U ) = AP ) ( + BP ( ) − ABP ( ) = k 9 1.14 We have k 8 − 10 k ) = 2 k + 7 f X x )( = − x e 1   2   0 −δ+ x ( 1 2 ,)3 x ≥ 0 , x < 0 k 8 10 . k

Probability Concepts 7 (a) fx(x) 1/2 (1/2) . . x 0 1 2 3 ∞ = ∫ 0 )(x x − e + 1 2 xδ ( 1[ 2 is a density function. )]3 dx − = ∞ ∫ 0 1 2 − x e dx + ∞ ∫ 0 1 2 x (δ − )3 dx = 1 2 + 1 2 = 1 . f X ∞ ∫ 0 Hence, dxx )( f X (a) P(X = 1) = 0 (the probability at a point of a continuous function is zero). =XP ( )3 = XP ( ≥ )1 = 1 2 ∞ ∫ 1 = 5.0 . f X dxx )( 1.15 += 1 2 ∞ ∫ 1 1 2 − x e dx = 1 − + e ) ( 1 1 2 = .0 6839 . fX(x) 1/4 . . . . x 1/8 -3 -2 -1 0 1 2 3 (a) The cumulative distribution function of X for all the range of x is, du = 1 8 x + 3 8 for −≤≤− 3 x 1 , x 1 ∫ 8 3 − 1 2 xF )( X = x ∫ ∞− f X duu )( = x and ∫ 1 − 3 4 and 1 4 du + 1 4 = x + ∫ 1 1 8 du = 1 4 x 8 x + for 1 ≤≤− x 1 , + 5 8 for 1 ≤≤ x 3 ,

8 and xFX 1)( = for Signal Detection and Estimation x ≥ 3 . Thus, FX (x) = x + 0 3 1 8 8 1 1 4 2 1 5 8 8 1 + + x x , x −< 3 , 1 −<≤− 3 x , 1 <≤− x 1 , 1 <≤ x 3 , x ≥ 3 (b) Calculating the area from the graph, we obtain 1.16 The density function is as shown 12)1 4 =

资料库

Signal Detection And Estimation - Solution Manual.pdf

相关推荐

课程资源

热门标签

最新资料