反卷积图像复原算法.docx

发布时间：2022-06-10 发布人：admin 分类：说明书资料大小：0.45M 资料格式：docx 举报版权申诉

zssyu0416-10535136-4744300845163498194.docx.pdf-第1页.png

第1页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第2页.png

第2页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第3页.png

第3页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第4页.png

第4页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第5页.png

第5页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第6页.png

第6页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第7页.png

第7页 / 共12页

zssyu0416-10535136-4744300845163498194.docx.pdf-第8页.png

第8页 / 共12页

文本预览

几种图像复原方法的对比一、Richardson-Lucy 算法 R-L 算法是目前世界上应用最广泛的函数恢复技术之一，它是一种迭代方法。MATLAB 提供的 deconvlucy（）函数还能够用于实现复杂图像重建的多种算法中，这些算法都基于 Lucy-Richardson 最大化可能性算法。 R-L 算法是一种迭代非线性复原算法，它是从最大似然公式推导出来的，图像用泊松分布加以模型化的。当下面这个迭代收敛时模型的最大似然函数就可以得到一个令人满意的方程：  ( , x y )   f f k 1  ( , x y )[ k ( , g x y  ) f  ) ( , x y ( , h x y k  ( , h x y )] ) 其中，*代表卷积，  代表相关，  f 代表未退化图像的估计，g 和 h 和以前定义一样。在 IPT 中，L-R 算法由名为 deconvlucy 的函数完成的。 deconvlucy()函数的调用格式：J=deconvlucy(I，PSF，NUMIT， DAMPAR，WEIGHT)。其中，I 表示输入图像，PSF 表示点扩散函数。其他参数都是可选参数：NUMIT 表示算法的迭代次数，默认为 10 次； DAMPAR 是一个标量，它指定了结果图像与原图像 I 之间的偏离阈值表，默认值为 0(无衰减）；WEIGHT 是一个与 I 同样大小的数组，它为每一个像素分配一个权重来反映其重量，表示像素加权值，默认值为原始图像的数值。图像复原源代码：

%% Deblurring Gray Images Using the Lucy-Richardson Algorithm clc clear close all I=imread('E:\lena512color.tif'); % 彩色图像的像素为 512*512 I1=rgb2gray(I); % 灰度图像的像素为 512*512 % figure,imshow(I),title('Original color image'); % figure,imshow(I1),title('Original gray image'); I2=I1(1:2:end,1:2:end); % 图像的像素设置为 256*256 figure,imshow(I2),title('Gray Image 256*256'); PSF = fspecial('gaussian',5,5); % 点扩散函数 Blurred = imfilter(I2,PSF,'symmetric','conv'); figure; imshow(Blurred); title('Gaussian Blurred'); V = 0.0001; BlurredNoisy = imnoise(Blurred,'gaussian',0,V); figure; imshow(BlurredNoisy); title('Blurred & Noisy');

K=size(I2); WT=zeros(K); WT(5:end-4,5:end-4)=1; J1 = deconvlucy(BlurredNoisy,PSF); % H1 = deconvlucy(BlurredNoisy,PSF,5); % 迭代 5 次 % H1_cell=deconvlucy({BlurredNoisy},PSF,5); % H2_cell=deconvlucy(H1_cell,PSF); % H2=im2uint8(H2_cell{2}); J2 = deconvlucy(BlurredNoisy,PSF,5,im2uint8(3*sqrt(V))); % 迭代 5 次 J3 =deconvlucy(BlurredNoisy,PSF,15,im2uint8(3*sqrt(V)));% 迭代 15 次 J4 =deconvlucy(BlurredNoisy,PSF,25,im2uint8(3*sqrt(V)));% 迭代 25 次 J5 =deconvlucy(BlurredNoisy,PSF,40,im2uint8(3*sqrt(V)));% 迭代 40 次 J6 =deconvlucy(BlurredNoisy,PSF,20,im2uint8(3*sqrt(V)),WT);% 迭代 20 次,加 WT J7 = deconvlucy(BlurredNoisy,PSF,40,im2uint8(3*sqrt(V)),WT); % 迭代 40 次,加 WT %

figure, imshow(J1); title('J1:deconvlucy(A,PSF)'); % figure, imshow(H1); title('H1:Restored Image NUMIT=5'); % figure,imshow(H2),title('H2:Restored Image NUMIT=15'); figure, imshow(J2); title('J2:deconvlucy(A,PSF,NUMIT=5,DAMPAR)'); figure, imshow(J3); title('J3:deconvlucy(A,PSF,NUMIT=15,DAMPAR)'); figure, imshow(J4); title('J4:deconvlucy(A,PSF,NUMIT=25,DAMPAR)'); figure, imshow(J5); title('J5:deconvlucy(A,PSF,NUMIT=40,DAMPAR)'); figure, imshow(J6), title('J6:deconvlucy(A,PSF,NUMIT=20,DAMPAR,WEIGHT)'); figure, imshow(J7), title('J7:deconvlucy(A,PSF,NUMIT=40,DAMPAR,WEIGHT)'); 二、维纳滤波维纳滤波法是由 Wiener 首先提出的，在图像复原领域，由于维纳滤波计算量小，复原效果好，从而得到了广泛的应用和发展。维纳滤波最开始主要应用在一维信号处理里，取得了比较不错的效果。之后，维纳滤波法也用于二维信号处理中，也取得了比较好的效果。维纳滤波器寻找一个统计误差函数：

2 e  {( fE   f 2 }) 最小的估计  f 。E 是期望值操作符， f 是未退化的图像。该表达式在频域可表示为  ( , ) F u v  [ 1 ( , ) H u v H u v ( , ) 2 其中， ),( vuH 表示退化函数 ),( vuH 2  ),( vuHvuH ),(  ( , ) H u v S u v  ( , ) / 2 f ] ( , ) G u v ( , ) S u v ),( vuH  表示 ),( vuH 的复共轭 ),( vuS   vuN 2),( 表示噪声的功率谱 ),( vuS f  2),( vuF 表示未退化图像的功率谱比率 ( , ) / fS u v ( , ) S u v  称为信噪功率比。在 IPT 中维纳滤波使用函数 deconvwnr 来实现的。维纳滤波能最佳复原的条件是要求已知模糊的系统函数，噪声功率谱密（或其自相关函数），原图像功率谱密度（或其自相关函数）。但实际上，原图像功率谱密度（或其自相关函数）一般难以获知，再加上维纳滤波是将图像假设为平稳随机场的前提下的最佳滤波，而实际的图像通常不能满足此前提。因此维纳滤波复原算法在实际中只能获得次最佳实施，它更多的是具有理论价值，被用作度量其他算法性能优劣的标杆。维纳滤波复原函数 deconvwnr()的调用格式：J=deconvwnr(I，PSF， NCORR，ICORR) 其中，I 表示输入图像，PSF 表示点扩散函数，NSR(默认值为 0)、

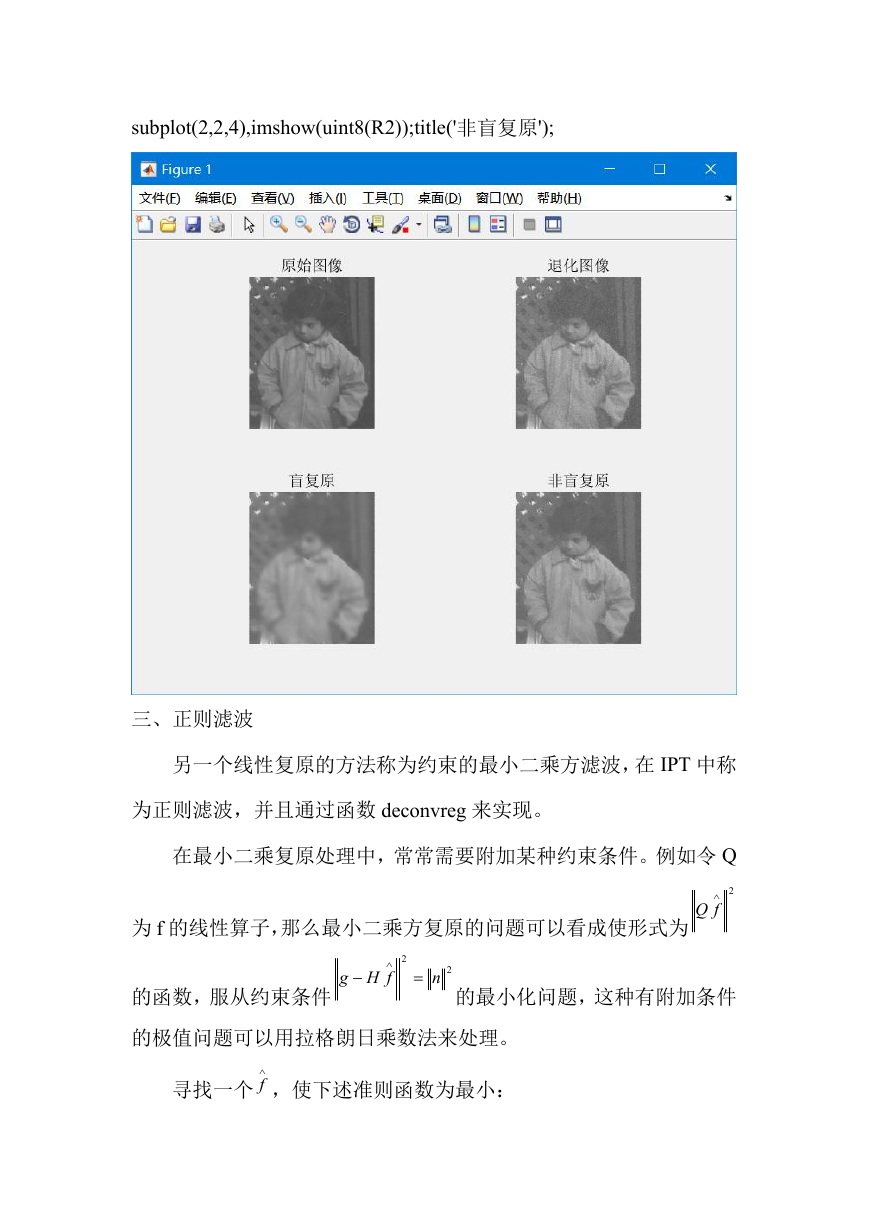
NCORR 和 ICORR 都是可选参数，分别表示信噪比、噪声的自相关函数、原始图像的自相关函数。输出参数 J 表示复原后的图像。维纳滤波复原源代码： % 维纳滤波在图像复原中的应用 clc clear close all I=imread('pout.tif'); % 原始图像 noise=5*randn(size(I)); % randn(1,lx)表示生成 1*lx 的矩阵，矩阵的每个元素都是随机数 noise=noise-min(min(noise)); % randn(size(I))是返回一个和 A 有同样维数大小的随机数组 J=double(I)+noise; R1=wiener2(J,[10 10]); % 未知噪声 R2=wiener2(J,[10 10],noise); % 已知噪声分布 figure subplot(2,2,1),imshow(uint8(I));title('原始图像'); subplot(2,2,2),imshow(uint8(J));title('退化图像'); subplot(2,2,3),imshow(uint8(R1));title('盲复原');

subplot(2,2,4),imshow(uint8(R2));title('非盲复原'); 三、正则滤波另一个线性复原的方法称为约束的最小二乘方滤波，在 IPT 中称为正则滤波，并且通过函数 deconvreg 来实现。在最小二乘复原处理中，常常需要附加某种约束条件。例如令 Q 为 f 的线性算子，那么最小二乘方复原的问题可以看成使形式为 2 fQ 的函数，服从约束条件 2  fHg  2  n 的最小化问题，这种有附加条件的极值问题可以用拉格朗日乘数法来处理。寻找一个  f ，使下述准则函数为最小：

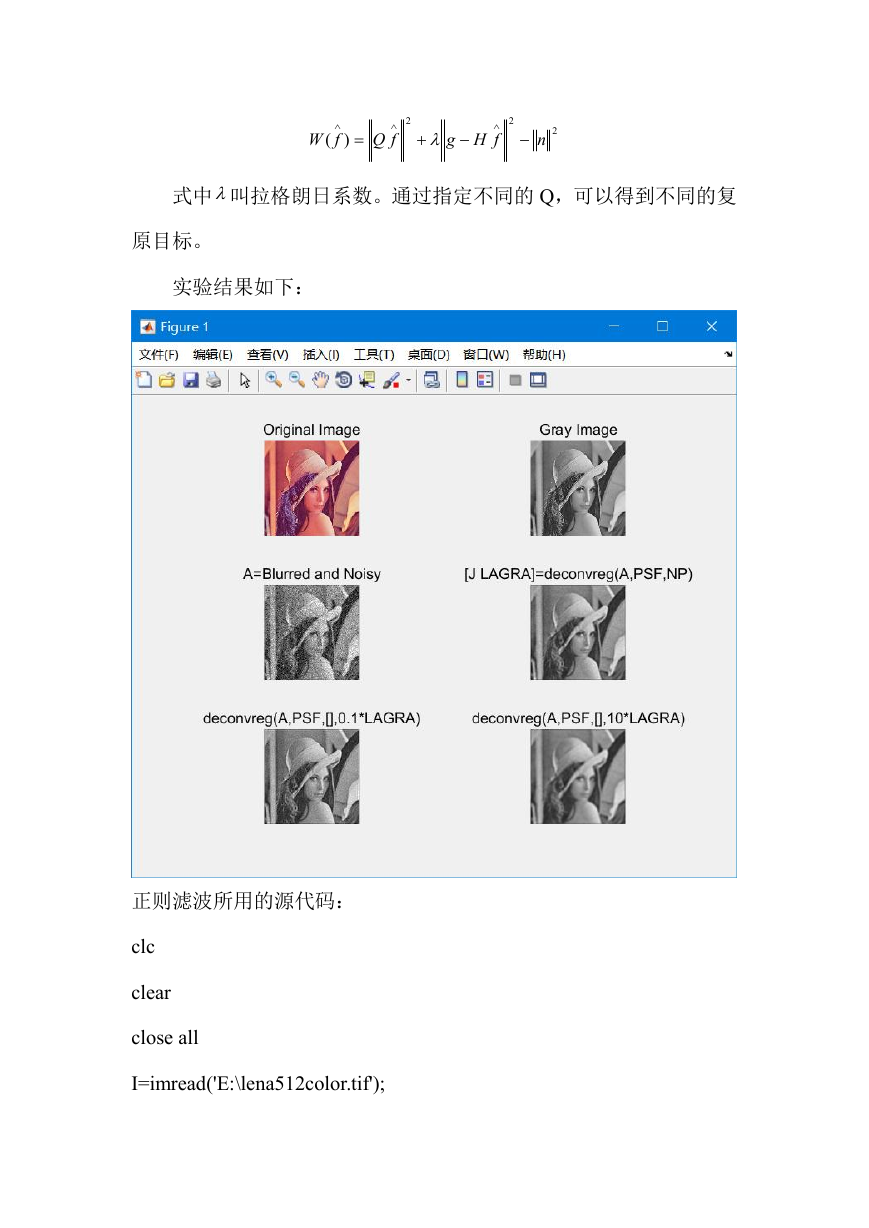
 ( fW )   fQ 2    fHg  2 2  n 式中叫拉格朗日系数。通过指定不同的 Q，可以得到不同的复原目标。实验结果如下：正则滤波所用的源代码： clc clear close all I=imread('E:\lena512color.tif');

分享到：

赞收藏

资料库

反卷积图像复原算法.docx

相关推荐

音视频

热门标签

最新资料