第1页 / 共23页
第2页 / 共23页
第3页 / 共23页
第4页 / 共23页
第5页 / 共23页
第6页 / 共23页
第7页 / 共23页
第8页 / 共23页
城市供水量预测数学建模问题及解答.doc
城市供水量预测
摘 要
本文对城市计划供水量进行了预测分析，并结合预测数据提出了具体的节水调价方
案。
首先，利用 Excel 软件对附件中的城市日用水量、水厂供水量、日最高、最低温度
等数据进行统计描述，并对原始数据进行预处理，剔除异常数据并利用插值方法补全数
据，以使所得数据能尽可能地反映客观实际。
接着，针对第一、二问提出的城市计划供水量和每个水厂的计划供水量预测问题，
在忽略温度影响的前提下建立回归分析与灰色系统 GM(1,1)组合预测模型，利用 SPSS
软件采用最小二乘法进行曲线拟合和参数求解，计算结果表明回归分析模型能够较精确
地进行大多数时间城市计划供水量的预测；在回归模型预测误差较大的情况下，建立灰
色系统 GM(1,1)预测模型，利用 Matlab 软件编程求解出其余时间的预测值，并与回归分
析模型的预测数据结合起来，得到最终的预测结果：2012 年 1 月的城市计划供水量为
4582.18 万吨，一、二号水厂计划供水量分别为 2840.37 万吨和 1766.92 万吨。此外,考
虑到数据具有季节性，采用时间序列分析的方法求解 1 月份各指标的预测值。在模型的
检验中对预测结果进行了残差检验，验证了预测结果精度优良。
随后，在对日最高、最低温度与日用水量的相关分析中，发现温度与用水量呈部分
相关，且在五至九月相关系数较大。进而在考虑温度影响下建立多元线性回归模型，将
气温因素对供水量的影响从总水量中提取出来进行预测，其方程与线性趋势项之和为最
终供水预测方程，根据方程求得 2012 年 1 月的城市计划供水量为 4882.53 万吨，一、二
号水厂计划供水量分别为 2862.54 万吨和 1800.70 万吨。
最后，针对第三问提出的水价调整问题，用需求价格弹性指数 E 刻画居民对水的需
求，进而建立水价与用水需求之间的函数关系，利用非线性回归求得水价调整预测方程，
并依据此方程分别求出在五、六、七、八月调价的四种调价方案对应的综合水价。
本文在结尾部分对城市供水量的不同预测模型和结果进行了精度分析和残差检验，
并指出了需要进一步研究的问题。
关键词：供水量预测；回归分析；灰色预测；时间序列；水价调整
- 1 -
一、问题重述
为了节约能源和水源，供水公司需要根据日供水量记录估计未来一时间段（未来一
天或一周）的用水量，以便安排未来（该时间段）的生产调度计划。
现在有某城市 7 年的历史记录，记录中给出了日期，每日用水量（吨/日）；当日的
最高温度和最低温度；一号水厂和二号水厂日供水量。
请充分地利用这些数据建立数学模型给出
1．预测 2012 年 1 月份城市的计划供水量。
2．预测 2012 年 1 月份城市中每个水厂的计划供水量。
3．由于水资源的匮乏，必须要节约水资源。除制定法规和加强宣传外，提高水价
格也是节水的主要措施。采用每年调一次水价的措施，希望 2012 年 8 月份的供水量不
超过 5045 万吨，请确定合理的水价调整方案。
附表 1：2005-2011 年的调价方案
调价日期
2005.05
2006.06
2007.05
2008.06
2009.07
20010.06
2011.08
3.0
3.4
3.9
4.3
4.7
5.0
5.2
调价后综合
水价（元/吨）
注：月初调整水价
二、模型假设
1. 假设短期内社会状况没有大的波动；
2. 假设两水厂的供水量能满足社会需求；
3. 假设对城市用水量的影响起决定性作用的因素主要是温度和价格；
4. 假设水价调整在一个周期内对每个月水需求量的影响相同。
三、符号说明
t ——时间；
K ——季节指数；
E ——需求价格弹性指数；
1P ——原水价；
2P ——调整后的水价；
1Q ——水价调整前的水需求量；
2Q ——水价调整后的水需求量；
四、问题分析
- 2 -
4.1 问题背景的理解
城市用水主要包括生活用水、生产用水、绿化用水以及其他不可预测水量等几部分，
其用水量总在不停地发生着变化。日用水量预测在各类城市用水预测中具有异常特殊的
地位，它不仅能直接指导水厂的生产，更能为水厂间的优化调度提供可靠的技术支持，
故比较准确地进行城市日、月用水量预测是非常重要的。
4.2 对建立供水量预测模型的分析
城市的供水量之所以难以准确预测，是因为影响该数据的因素太多，这些因素包括
社会的、经济的、政治的、科技的等等。目前为止，还没有一个统一的、完整的、普遍
适用的预测方法可供使用。
出于以上考虑，我们需要根据用水量变化的不同规律分别建立不同的数学模型。
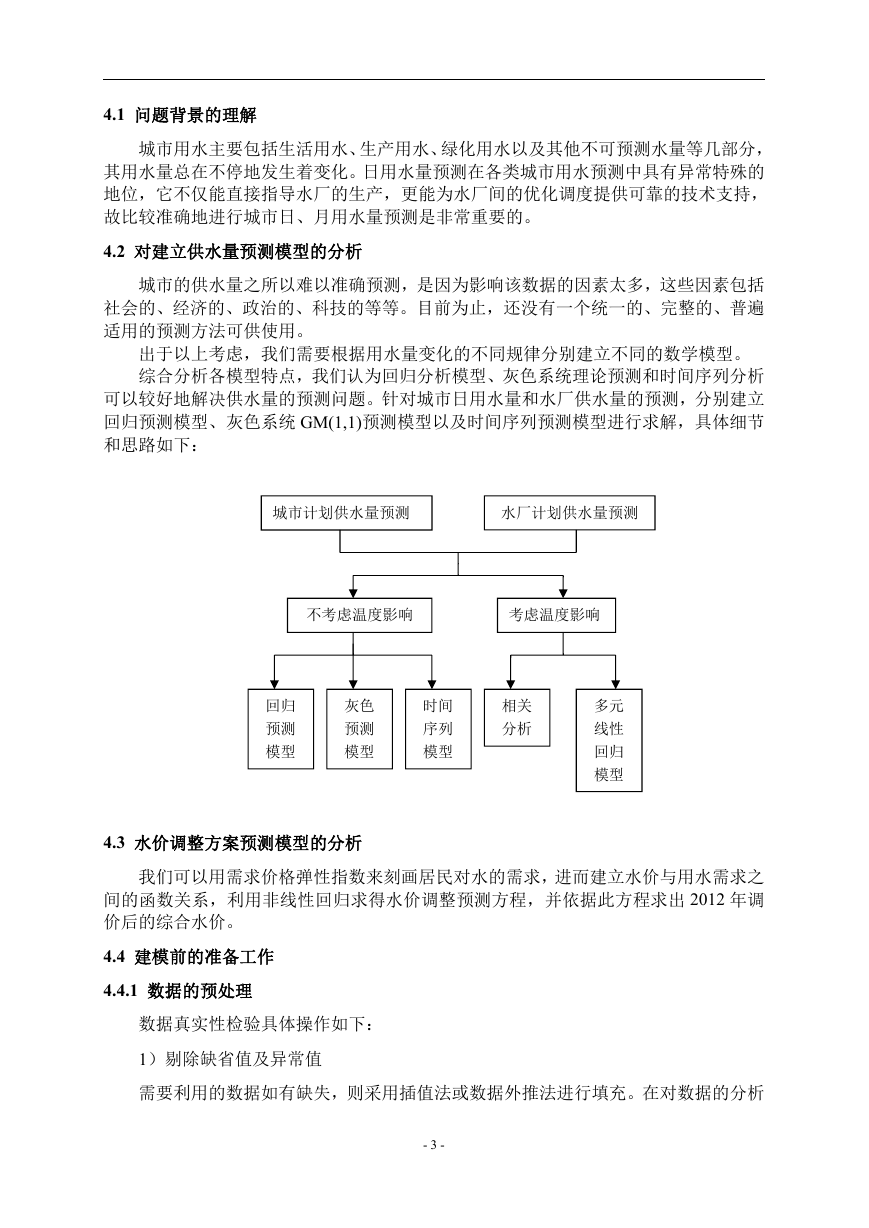
综合分析各模型特点，我们认为回归分析模型、灰色系统理论预测和时间序列分析
可以较好地解决供水量的预测问题。针对城市日用水量和水厂供水量的预测，分别建立
回归预测模型、灰色系统 GM(1,1)预测模型以及时间序列预测模型进行求解，具体细节
和思路如下：
城市计划供水量预测
水厂计划供水量预测
不考虑温度影响
考虑温度影响
回归
预测
模型
灰色
预测
模型
时间
序列
模型
相关
分析
多元
线性
回归
模型
4.3 水价调整方案预测模型的分析
我们可以用需求价格弹性指数来刻画居民对水的需求，进而建立水价与用水需求之
间的函数关系，利用非线性回归求得水价调整预测方程，并依据此方程求出 2012 年调
价后的综合水价。
4.4 建模前的准备工作
4.4.1 数据的预处理
数据真实性检验具体操作如下：
1）剔除缺省值及异常值
需要利用的数据如有缺失，则采用插值法或数据外推法进行填充。在对数据的分析
- 3 -
中可以看出：日最低温度为零时，部分数据出现异常（甚至大于最高温度），可以判断
此时为数据缺失，应该予以填充。
采用统计上最常用的 3法则对异常点进行诊断，若确实有问题，则将这部分数据
剔除并沿用上述方法修正。对仍然有疑问的数据，在不影响求解精度的前提下可以考虑
将其剔除。
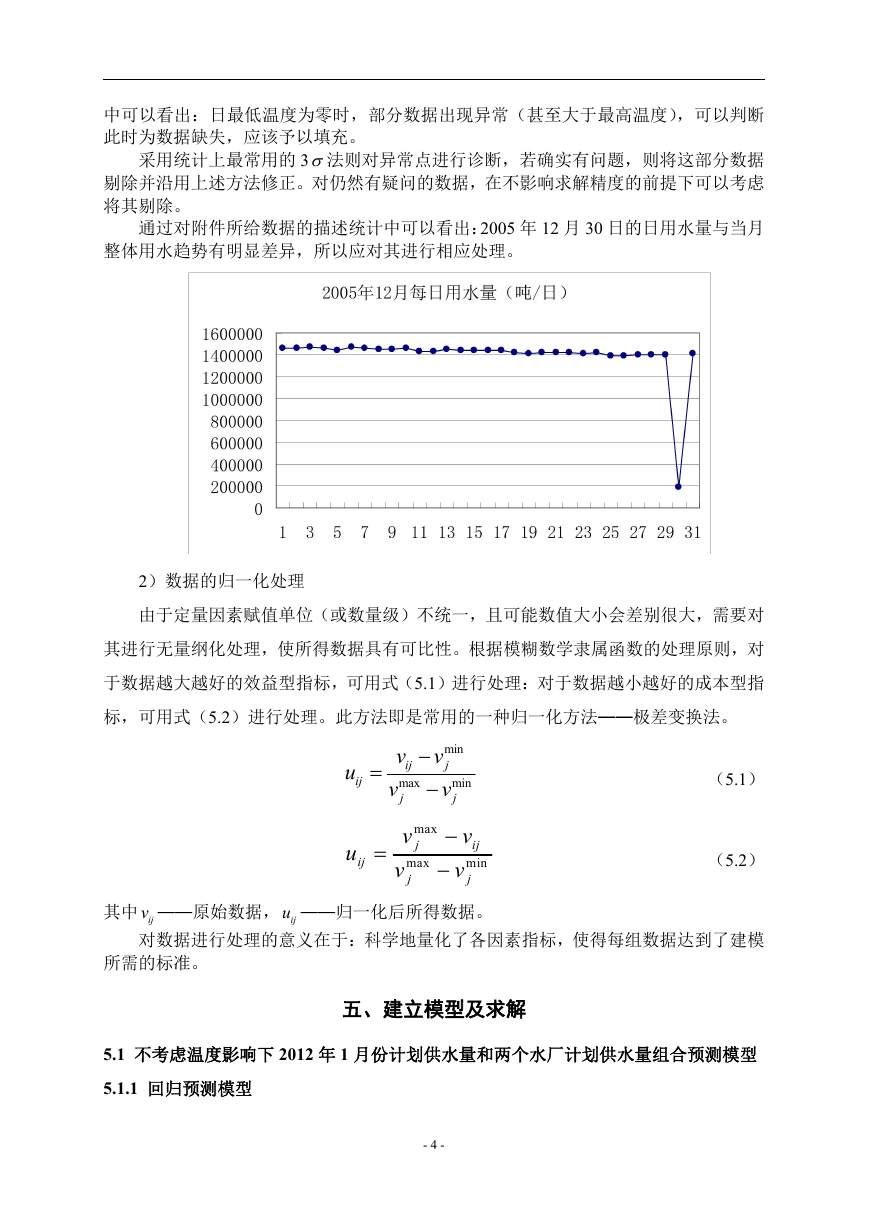
通过对附件所给数据的描述统计中可以看出：2005 年 12 月 30 日的日用水量与当月
整体用水趋势有明显差异，所以应对其进行相应处理。
2）数据的归一化处理
由于定量因素赋值单位（或数量级）不统一，且可能数值大小会差别很大，需要对
其进行无量纲化处理，使所得数据具有可比性。根据模糊数学隶属函数的处理原则，对
于数据越大越好的效益型指标，可用式（5.1）进行处理：对于数据越小越好的成本型指
标，可用式（5.2）进行处理。此方法即是常用的一种归一化方法——极差变换法。
u
ij
u
ij
min
v
v
ij
j
max
v
v
j
v
max
v
j
max
j
min
j
v
ij
min
v
j
（5.1）
（5.2）
其中 ijv ——原始数据， iju ——归一化后所得数据。
对数据进行处理的意义在于：科学地量化了各因素指标，使得每组数据达到了建模
所需的标准。
五、建立模型及求解
5.1 不考虑温度影响下 2012 年 1 月份计划供水量和两个水厂计划供水量组合预测模型
5.1.1 回归预测模型
- 4 -
回归预测模型的建立
利用处理后的数据，我们首先用 SPSS 软件进行曲线拟合与参数估计，通过对各统
计量的分析和比较，最终得出回归预测方程。
根据处理后的数据，分别以时间变化为自变量t ，建立回归模型：
在 SPSS 软件中，调用【Analyze】 【Regression】 【Curve Estimation...】，
采用最小二乘法对上述模型的参数进行求解，综合考虑 2R 、 F 和 P 值统计量，分别选
取下述函数进行曲线拟合:
二次曲线模型(Quadratic)：
三次曲线模型(Cubic)：
对数曲线模型(Logarithmic)：
生长曲线模型(Growth)：
s 曲线模型(S-curve)：
幂指数曲线模型(Power)：
y
b
0
b t b t
1
2
2
y
b
0
b t b t
1
2
2
3
b t
3
y
b
0
1 ln
b
t
y
eb
0
b t
1
y
b
e
0
b t
1
y
b t
0
b
1
（5.3）
（5.4）
（5.5）
（5.6）
（5.7）
（5.8）
求解上述回归方程时，需对 2R 、F值和 P值统计量进行分析。现以 2012 年 1 月的
一组数据为例，对几种拟合程度较好的曲线模型作比较分析（见表 1）。
表 1：参数检验分析表
二次曲线
(Quadratic)
0.997
672.153
三次曲线
(Cubic)
0.998
446.123
2R 统计量
F 统计量
幂指数曲线
对数曲线
(Power)
0.997
1472.678
(Logarithmic)
0.995
1073.734
P 值 8.80122e-006 0.000179439 2.26402e-007 4.97437e-007
统计量说明： 2R ——可决系数；
F ——回归方程的显著性检验；
P 值——相伴概率，一般要求的范围之内（P < 0.01）。
在曲线拟合中 2R 、 F 和 P 值统计量对拟合效果有重要意义， 2R 表示自变量所能解
释的方差在总方差中所占的百分比，其取值越接近于 1 说明模型的效果越好；F 统计量
- 5 -
表示因变量与自变量之间的线性关系是否显著，一般取值为 12， F 值大于规定值，则
表示显著，否则不显著，其值越大说明越显著；P 值的大小表征回归系数和零是否存在
显著差异。选择预测模型时应综合考虑上述指标。
然后，通过所求日用水量及日两个水厂供水量的回归方程（详见附录一），可以直
接得到大部分 2012 年 1 月份计划供水量预测值（见表 2）和一部分两个水厂供水量预测
值（见表 3、表 4）。
5.1.2 灰色系统 GM(1,1)预测模型
GM(1,1)模型的建立
由于统计数据信息不完整，故有部分日用水量数据和 70%以上的水厂日供水量数据
采用曲线拟合法进行回归分析不能得到令人满意的结果，所以我们考虑用对信息质量要
求不高的灰色系统分析法进行预测，建立 GM(1,1)模型。
记
x
),1((
x
x
2(
),...
(
nx
)),
其中 )(ix 表示第i 年数值。
Step1：令 )0(x 为 GM（1，1）建模序列，表示灰导数
其中
(0)
x
(
x
(0)
(1),
x
(0)
(2),...,
x
(0)
( ))
n
x
)()0(
k
)(
kx
，
...3,2,1k
Step2：令 )1(x 为 )0(x 的 AGO 序列，对 )0(x 作累加生成，即得到新的序列 )1(x ，
(1)
x
(1)
(
x
(1),
x
(1)
(2),...,
x
(1)
( ))
n
(1)
x
(1)
x
(0)
(1)
(1)
x
( )
k
k
m
1
(0)
x m
(
)
Step3：令 )1(z 为 )1(x 的均值（MEAN）序列，表示白化背景值
(1)
z
( ) 0.5
k
x
(1)
( ) 0.5
k
x
(1)
(
k
1)
（5.9）
(1)
(2),
z
(1)
(3),...,
z
(1)
( ))
n
)(
k
az
)1(
)(
k
b
（5.10）
(1)
(
z
则得到 GM(1,1)的灰微分方程模型为
)0(
x
z
a、 为待估计参数，分别称为发展灰度和内生控制灰度。
式中： b
其中，
- 6 -
n
k
2
n
k
2
a
b
n
k
2
)1
n
k
n
2
(
经变换后得到
GM(1,1)模型的求解
)1(
z
)(
k
)0(
x
)(
k
(
n
(
n
)1(
z
2
)(
k
(
n
k
2
n
)1
2
z
k
n
k
2
)1(
z
)(
xk
)0(
)(
k
;
)1(
2
))(
k
)1(
z
)(
k
)1(
z
2
)(
k
)1(
z
)(
k
)1(
z
)(
xk
)0(
)(
k
n
2
k
)(
k
2
n
2
k
z
)1(
2
))(
k
)1
n
k
2
)1(
z
(
n
k
2
)0(
x
)(
k
b
az
)1(
)(
k
（5.11）
在（5.11）两端同时乘以 ake 得，
(0)
ak
e x
( )
k
ak
e az
(1)
( )
k
ak
e b
即
z
(1)( )
k
e
ak
ak
(
be d C
t
)
将代入上式中，可得
Ce
ak
b
a
C x
0(1) b
a
于是得出时间函数 (1)(
x
k 的估计值
1)
(1)
ˆ
x
(
k
1)
[
x
0
(1)
b
a
ak
]
e
b
a
（5.12）
我们把上式（5.12）作为预测方程。利用 Matlab 软件编程求解出相应的预测值。具
体程序见附录二。
不考虑温度的影响下的求解结果
根据以上模型对 2012 年 1 月份城市的计划供水量进行预测，结果如下表 2，结合回
归分析的求解结果，得出两水厂的计划供水量预测值，整理成表 3、4。
表 2：2012 年 1 月份城市的计划供水量预测值
日期
1 月 1 日
1 月 2 日
1 月 3 日
1 月 4 日
1 月 5 日
供水量（吨）
1521242.63
1362306.51
1449004.28
1460112.01
1516183.61
- 7 -
日期
1 月 17 日
1 月 18 日
1 月 19 日
1 月 20 日
1 月 21 日
供水量（吨）
1462086.37
1496396.01
1500952.01
1472172.85
1499611.53
1 月 6 日
1 月 7 日
1 月 8 日
1 月 9 日
1 月 10 日
1 月 11 日
1 月 12 日
1 月 13 日
1 月 14 日
1 月 15 日
1 月 16 日
1437401.75
1469847.79
1469772.26
1471213.69
1469697.36
1527921.16
1493817.90
1461178.20
1499372.56
1465656.42
1431908.73
1 月 22 日
1 月 23 日
1 月 24 日
1 月 25 日
1 月 26 日
1 月 27 日
1 月 28 日
1 月 29 日
1 月 30 日
1 月 31 日
供水总量
1502853.59
1473645.76
1463915.12
1500058.54
1494927.33
1511493.45
1466198.35
1485177.60
1502753.89
1482900.00
45821779.26
通过累加求和的方法可以计算出 2012 年 1 月份计划总供水量为 4582.18 万吨。
表 3：2012 年 1 月份城市中一号水厂的计划供水量
日期
1 月 1 日
1 月 2 日
1 月 3 日
1 月 4 日
1 月 5 日
1 月 6 日
1 月 7 日
1 月 8 日
1 月 9 日
1 月 10 日
1 月 11 日
1 月 12 日
1 月 13 日
1 月 14 日
1 月 15 日
1 月 16 日
日期
1 月 1 日
1 月 2 日
1 月 3 日
1 月 4 日
1 月 5 日
1 月 6 日
1 月 7 日
1 月 8 日
1 月 9 日
供水量（吨）
988807.78
885499.41
915932.68
862730.16
844237.47
874989.25
958702.43
952986.44
956289.23
928118.70
883121.16
841800.78
889071.54
977098.59
952676.89
930740.93
日期
1 月 17 日
1 月 18 日
1 月 19 日
1 月 20 日
1 月 21 日
1 月 22 日
1 月 23 日
1 月 24 日
1 月 25 日
1 月 26 日
1 月 27 日
1 月 28 日
1 月 29 日
1 月 30 日
1 月 31 日
供水总量
供水量（吨）
928911.36
874998.21
841417.56
891180.43
971195.15
976855.12
957661.83
933296.57
877426.42
838861.79
860156.32
944199.02
965365.53
976790.95
922603.73
28403723.43
表 4：2012 年 1 月份城市中二号水厂的计划供水量
供水量（吨）
516863.70
504892.18
556468.66
626142.79
671523.87
588972.20
529419.85
513136.79
514924.34
- 8 -
日期
1 月 17 日
1 月 18 日
1 月 19 日
1 月 20 日
1 月 21 日
1 月 22 日
1 月 23 日
1 月 24 日
1 月 25 日
供水量（吨）
563953.90
634942.89
668974.54
598883.01
536498.42
525998.92
515684.28
567234.58
676113.39
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
