线激光扫描技术报告PDF.pdf-资料库

第1页 / 共16页

第2页 / 共16页

第3页 / 共16页

第4页 / 共16页

第5页 / 共16页

第6页 / 共16页

第7页 / 共16页

第8页 / 共16页

线激光扫描技术报告摘要本技术报告描述了线激光测距方法，主要包括相机标定、线激光平面标定、线激光三角法、水下应用时折射成像校准。关键字：相机标定线激光三角法水下相机标定相机的标定很多的计算机视觉任务需要计算所拍摄物体的几何信息，如目标测量、三维重建等，这就需要指导相机的成像参数，有些参数可以从相机的产品参数中获得，比如成像传感器（CMOS、CCD）的尺寸和像素分辨率、像素尺寸、镜头焦距等；然而有些参数是未知的，这就需要进行标定计算获得。相机的标定是指通过相机所拍摄的图像计算相机的内外参数。内外参数描述了三维空间中点与图像像素的关系。内参描述相机的内部属性，外参描述相机在三维世界的位姿。为了使运算简便，通常采用小孔成像模型，这部分内容可以在《计算机视觉：一种现代方法》这本书里阅读详细的内容。小孔成像的原理如下图所示：坐标系

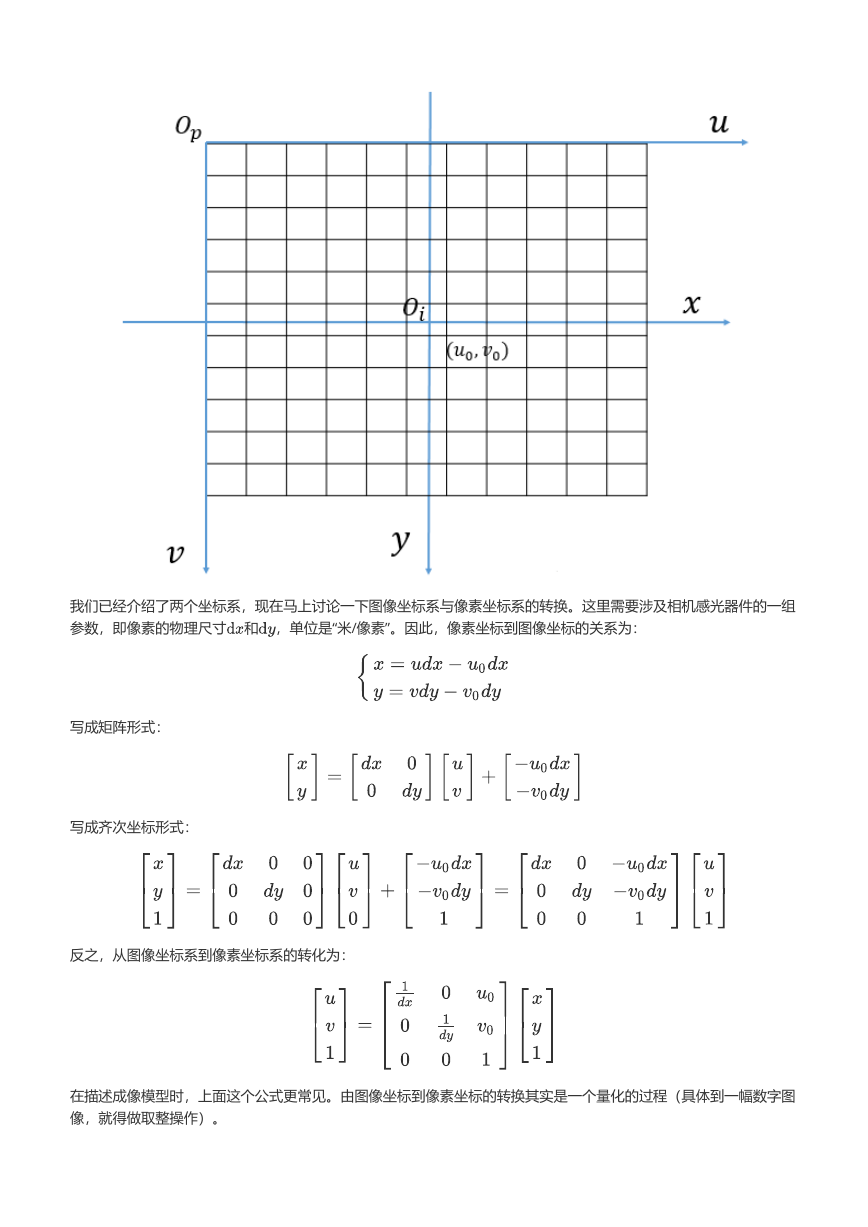
在讨论成像模型的过程中，我们会用到4个不同的坐标系：像素坐标系、图像坐标系、相机坐标系、世界坐标系。这样做的好处是在不同的坐标系里面方便用数学公式对相应的问题进行建模，然后把坐标系之间的关系描述出来，就完成了整个成像的建模，算是一种分而治之的思想。首先来看看在我们处理成像建模问题时，手里仅有的东西：数字栅格图像。 1. 像素坐标系像素坐标系是我们对图像中的像素进行索引定位时建立的坐标系，一般以图像左上角为原点，向右为轴，向下为轴。我们所说的第列第行像素的坐标就是不是说像素坐标系的坐标值都必须是整数，比如亚像素级的坐标就有小数部分。。可见，图像像素在像素坐标系上的坐标都是整数。但这并， 2. 图像坐标系像素坐标系描述的是图像像素的坐标，无法反映图像中物体的实际物理尺寸。根据小孔成像原理，3D世界在成像平面上成像，在这个成像平面上建立一个坐标系，即是图像坐标系。该坐标系的和轴分别与像素坐标系的轴和轴平行和同向，原点是相机光轴与成像平面的交点，因此和像素坐标系相比有一个偏移量。除非特别说明，一般我们用小写字母表示二维平面上的点，用大写字母表示三维空间的点。

我们已经介绍了两个坐标系，现在马上讨论一下图像坐标系与像素坐标系的转换。这里需要涉及相机感光器件的一组参数，即像素的物理尺寸和，单位是“米/像素”。因此，像素坐标到图像坐标的关系为：写成矩阵形式：写成齐次坐标形式：反之，从图像坐标系到像素坐标系的转化为：在描述成像模型时，上面这个公式更常见。由图像坐标到像素坐标的转换其实是一个量化的过程（具体到一幅数字图像，就得做取整操作）。

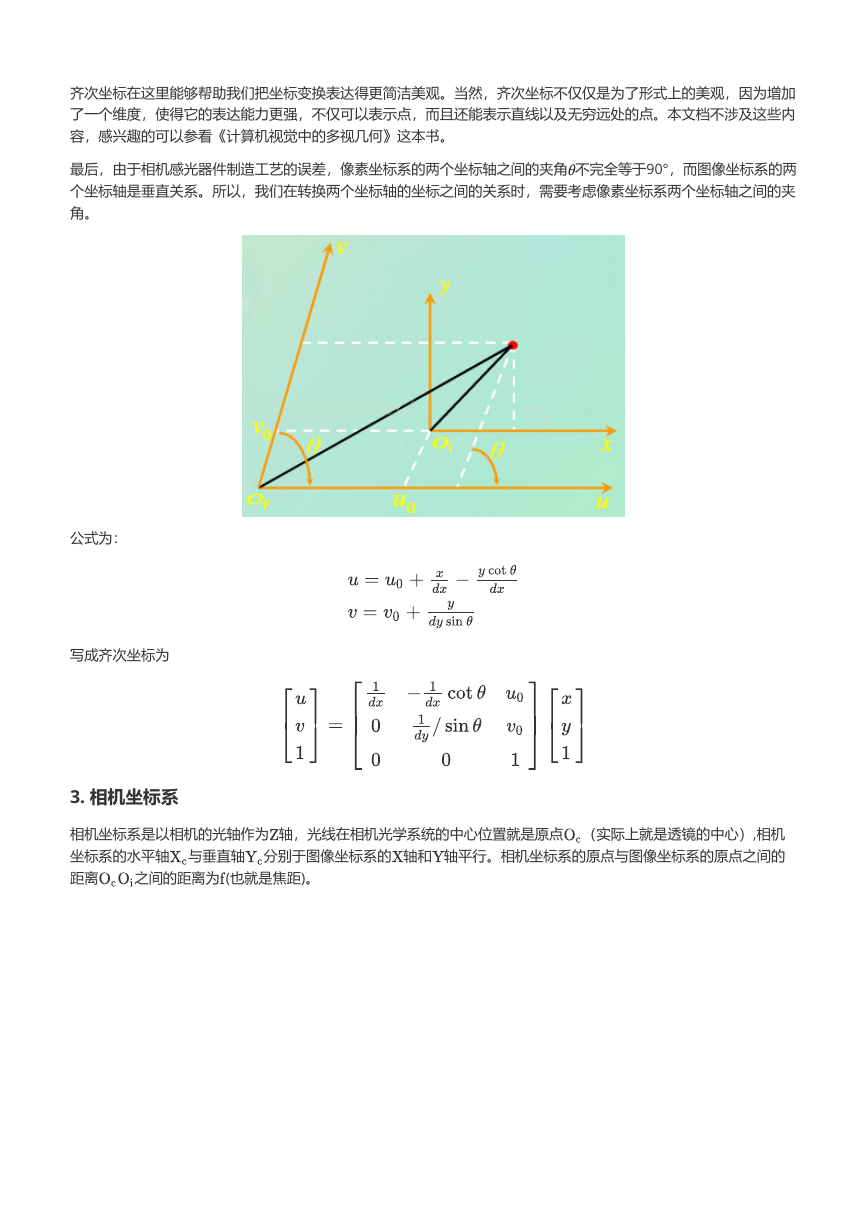
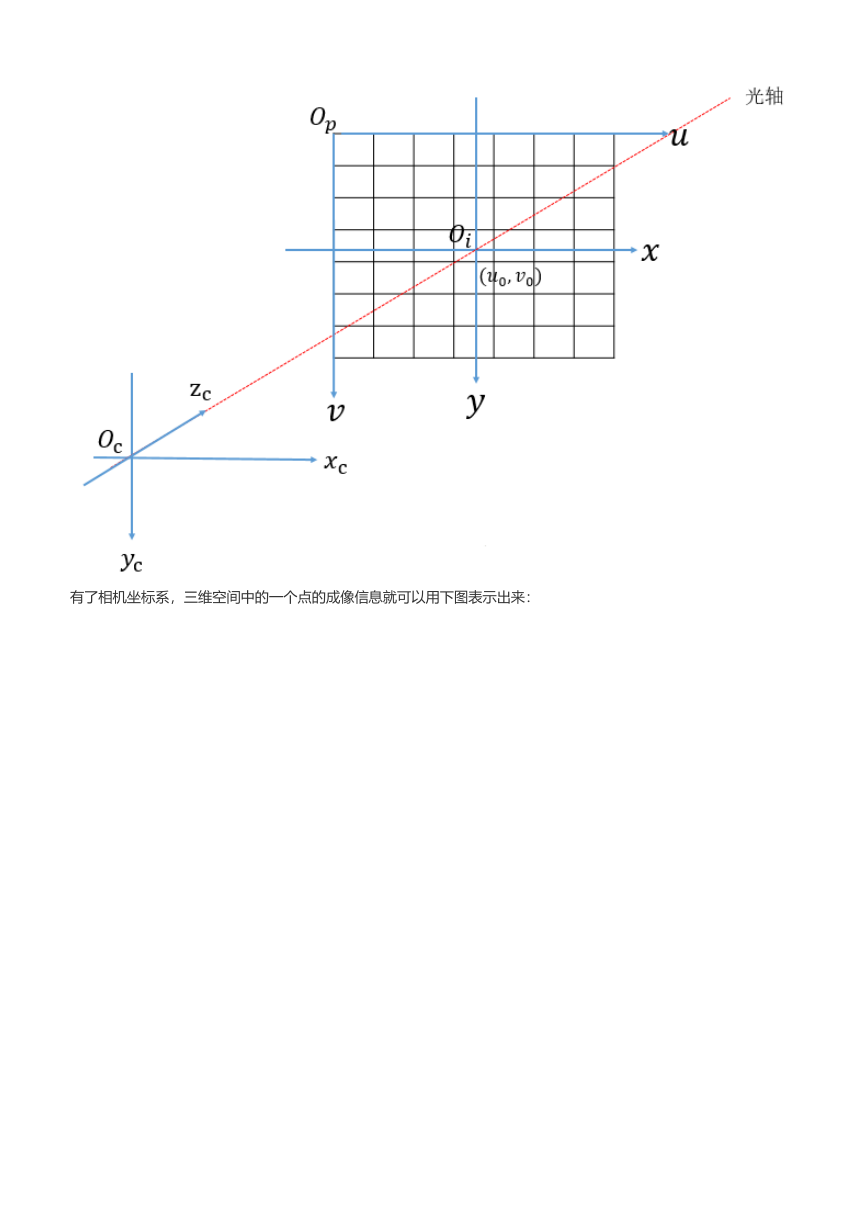
齐次坐标在这里能够帮助我们把坐标变换表达得更简洁美观。当然，齐次坐标不仅仅是为了形式上的美观，因为增加了一个维度，使得它的表达能力更强，不仅可以表示点，而且还能表示直线以及无穷远处的点。本文档不涉及这些内容，感兴趣的可以参看《计算机视觉中的多视几何》这本书。最后，由于相机感光器件制造工艺的误差，像素坐标系的两个坐标轴之间的夹角不完全等于90°，而图像坐标系的两个坐标轴是垂直关系。所以，我们在转换两个坐标轴的坐标之间的关系时，需要考虑像素坐标系两个坐标轴之间的夹角。公式为：写成齐次坐标为 3. 相机坐标系相机坐标系是以相机的光轴作为轴，光线在相机光学系统的中心位置就是原点（实际上就是透镜的中心）,相机坐标系的水平轴与垂直轴分别于图像坐标系的轴和轴平行。相机坐标系的原点与图像坐标系的原点之间的距离之间的距离为 (也就是焦距)。

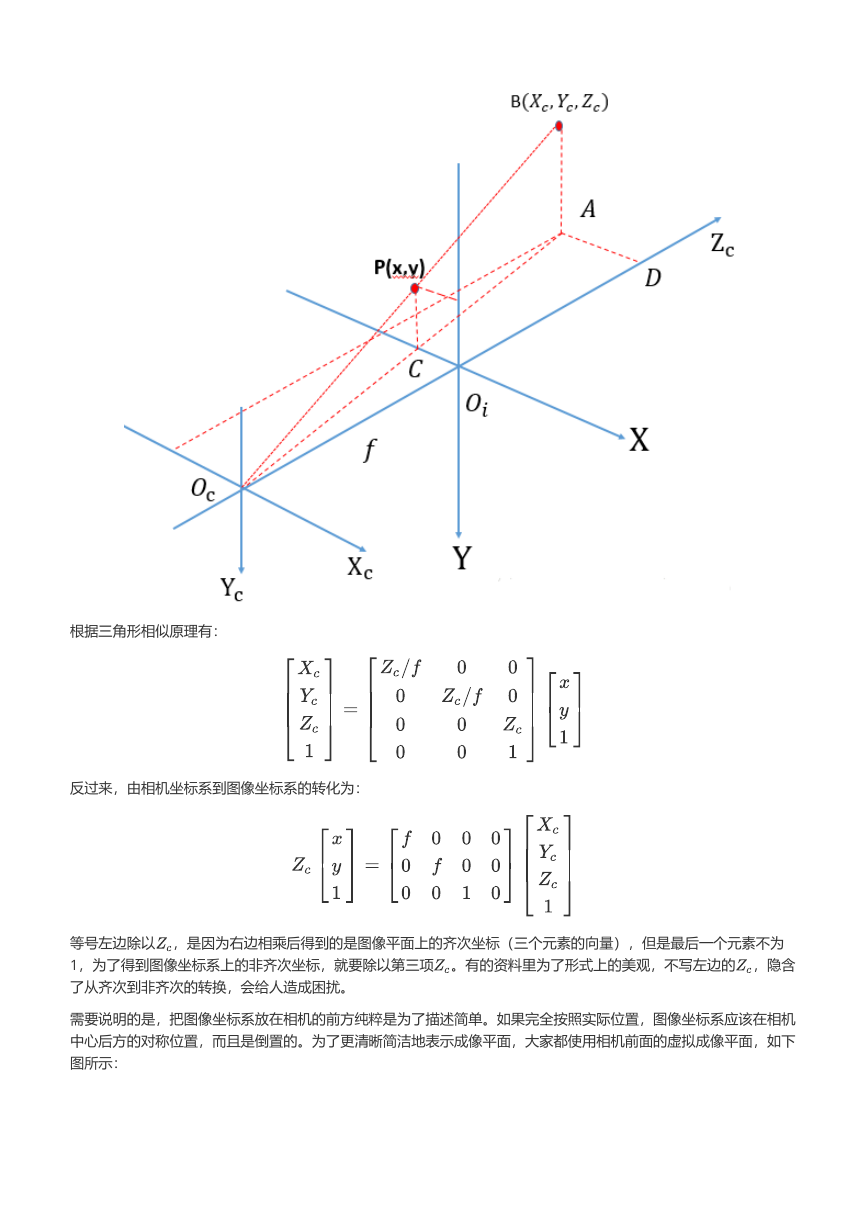
有了相机坐标系，三维空间中的一个点的成像信息就可以用下图表示出来：

根据三角形相似原理有：反过来，由相机坐标系到图像坐标系的转化为：等号左边除以，是因为右边相乘后得到的是图像平面上的齐次坐标（三个元素的向量），但是最后一个元素不为 1，为了得到图像坐标系上的非齐次坐标，就要除以第三项。有的资料里为了形式上的美观，不写左边的，隐含了从齐次到非齐次的转换，会给人造成困扰。需要说明的是，把图像坐标系放在相机的前方纯粹是为了描述简单。如果完全按照实际位置，图像坐标系应该在相机中心后方的对称位置，而且是倒置的。为了更清晰简洁地表示成像平面，大家都使用相机前面的虚拟成像平面，如下图所示：

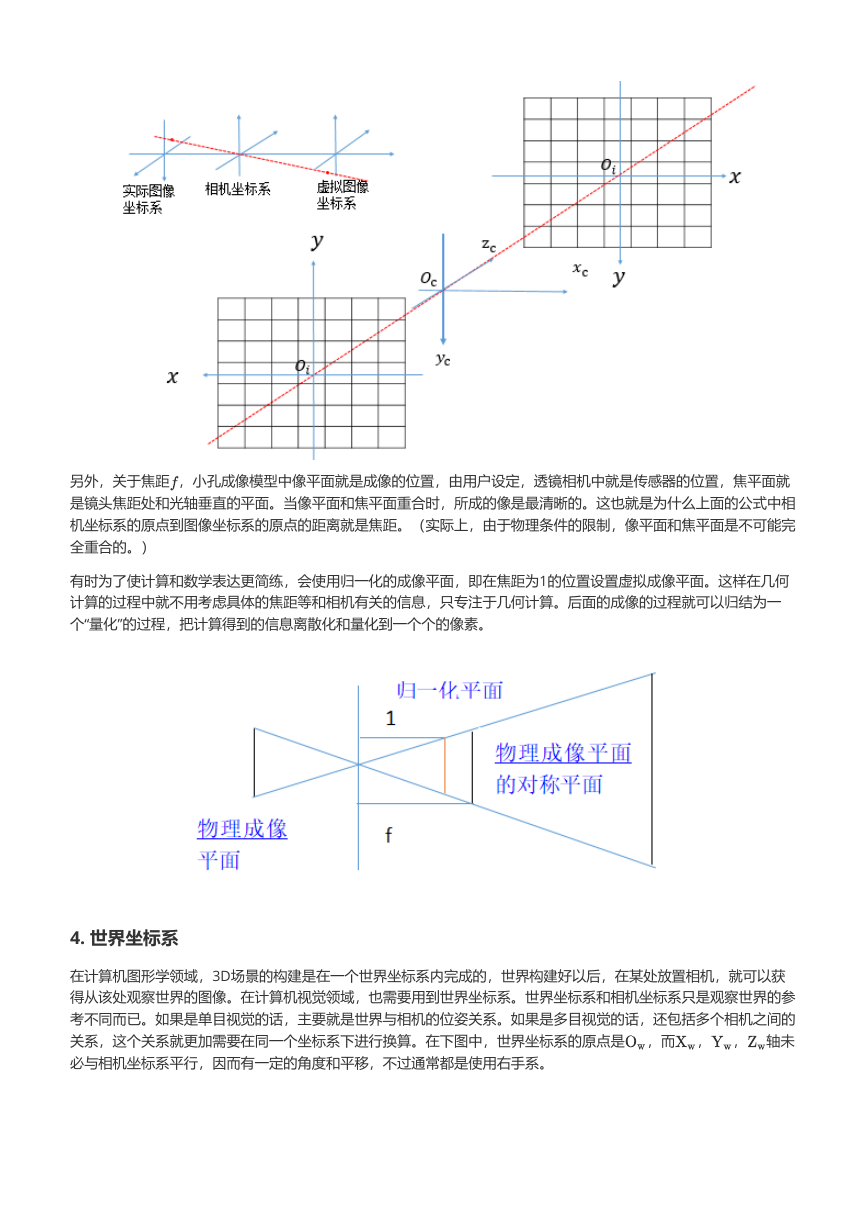
另外，关于焦距，小孔成像模型中像平面就是成像的位置，由用户设定，透镜相机中就是传感器的位置，焦平面就是镜头焦距处和光轴垂直的平面。当像平面和焦平面重合时，所成的像是最清晰的。这也就是为什么上面的公式中相机坐标系的原点到图像坐标系的原点的距离就是焦距。（实际上，由于物理条件的限制，像平面和焦平面是不可能完全重合的。）有时为了使计算和数学表达更简练，会使用归一化的成像平面，即在焦距为1的位置设置虚拟成像平面。这样在几何计算的过程中就不用考虑具体的焦距等和相机有关的信息，只专注于几何计算。后面的成像的过程就可以归结为一个“量化”的过程，把计算得到的信息离散化和量化到一个个的像素。 4. 世界坐标系在计算机图形学领域，3D场景的构建是在一个世界坐标系内完成的，世界构建好以后，在某处放置相机，就可以获得从该处观察世界的图像。在计算机视觉领域，也需要用到世界坐标系。世界坐标系和相机坐标系只是观察世界的参考不同而已。如果是单目视觉的话，主要就是世界与相机的位姿关系。如果是多目视觉的话，还包括多个相机之间的关系，这个关系就更加需要在同一个坐标系下进行换算。在下图中，世界坐标系的原点是，而，，轴未必与相机坐标系平行，因而有一定的角度和平移，不过通常都是使用右手系。

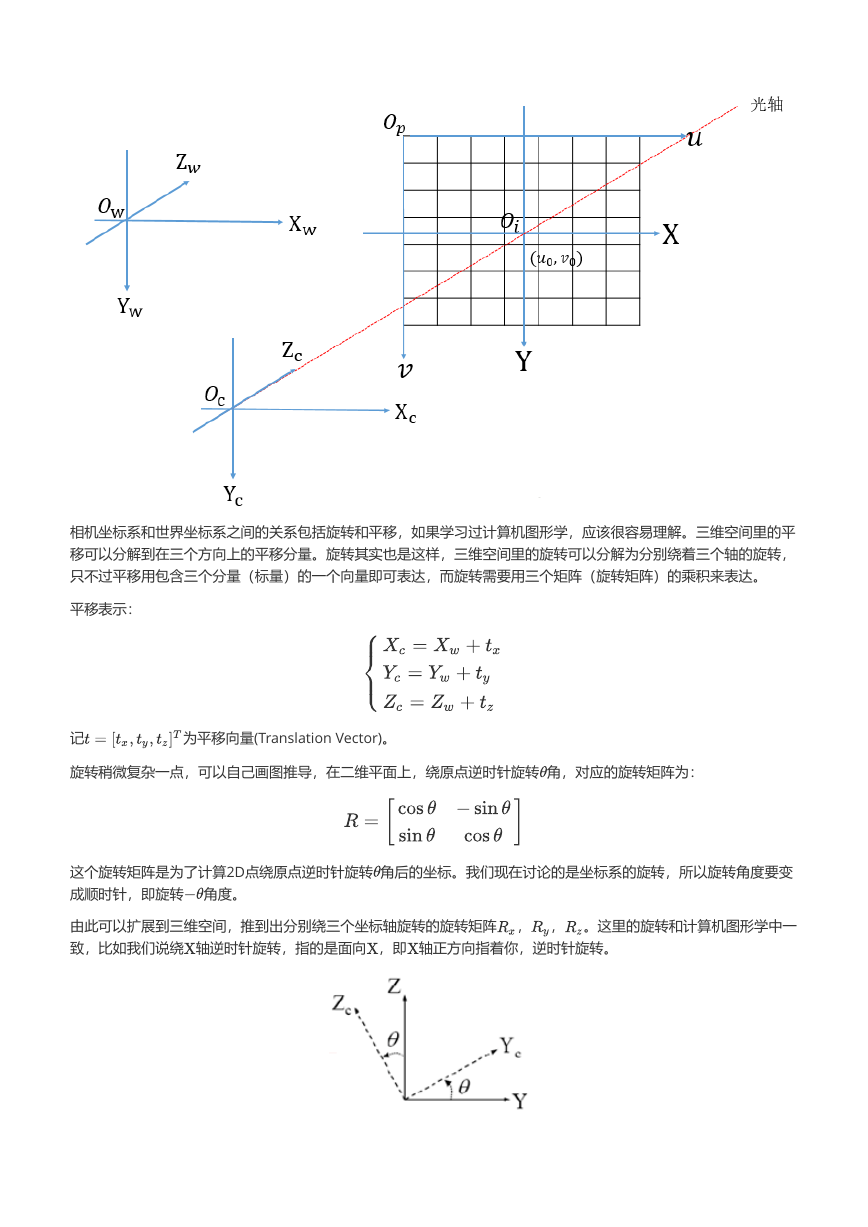
相机坐标系和世界坐标系之间的关系包括旋转和平移，如果学习过计算机图形学，应该很容易理解。三维空间里的平移可以分解到在三个方向上的平移分量。旋转其实也是这样，三维空间里的旋转可以分解为分别绕着三个轴的旋转，只不过平移用包含三个分量（标量）的一个向量即可表达，而旋转需要用三个矩阵（旋转矩阵）的乘积来表达。平移表示：记为平移向量(Translation Vector)。旋转稍微复杂一点，可以自己画图推导，在二维平面上，绕原点逆时针旋转角，对应的旋转矩阵为：这个旋转矩阵是为了计算2D点绕原点逆时针旋转角后的坐标。我们现在讨论的是坐标系的旋转，所以旋转角度要变成顺时针，即旋转角度。由此可以扩展到三维空间，推到出分别绕三个坐标轴旋转的旋转矩阵，，。这里的旋转和计算机图形学中一致，比如我们说绕轴逆时针旋转，指的是面向，即轴正方向指着你，逆时针旋转。

资料库

线激光扫描技术报告PDF.pdf

相关推荐

课程资源

热门标签

最新资料