红外热成像基础知识.pdf-资料库

philip1106-9365201-4744300845209614950.pdf-第1页.png

第1页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第2页.png

第2页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第3页.png

第3页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第4页.png

第4页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第5页.png

第5页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第6页.png

第6页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第7页.png

第7页 / 共18页

philip1106-9365201-4744300845209614950.pdf-第8页.png

第8页 / 共18页

本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 什么是红外热成像？从目标到红外热图如图所示，左边是一张热像片，右边是与之相对应的普通照片。这也是红外线应用的一例。热像片或热图和普通相片的关系紧密。当我们试着解释热图如何形成时，很容易看到它与普通摄像术的相似之处。在我们生活的这个世界里，绝大多数时间我们被各种类型的光所包围。也许我们不是总记着，但是这些光几乎无例外地来自很热的源物体。最通常的来源是太阳。然而，热的源物体可以是白炽灯，光弧，火花以及事实上的任何物体，只要它们发射辐射。想想图中的灯泡。实际上这是种特殊的高亮度灯泡，用于机场等处。此灯泡外壳的温度极高。关掉电源，灯灭了。用手不接触灯泡来感觉，可以感到关灯后灯泡可以热很长一段时间。灯泡关掉了，但热辐射会持续挺长一段时间。事实上温度超过绝对零度即 –273º C 的物体都辐射热。热红外成像是借助于目标的热辐射以得到其热图的一项技术。热辐射的性质在很大程度上和可见光的性质相同或相似。热红外成像使我们人类可以看见并理解热像仪所“看到”的。即象一张不同灰度或不同色彩的照片。它不仅可以帮助我们看热的变化，还是量化这些变化的一项技术。 _____________________________________________________________________ 1-IRSV.CN-18611194295//861052459970 V1.0 25.7癈36.3癈303578.7癈939.1癈500SP01: 915.7癈SP02: 809.7癈

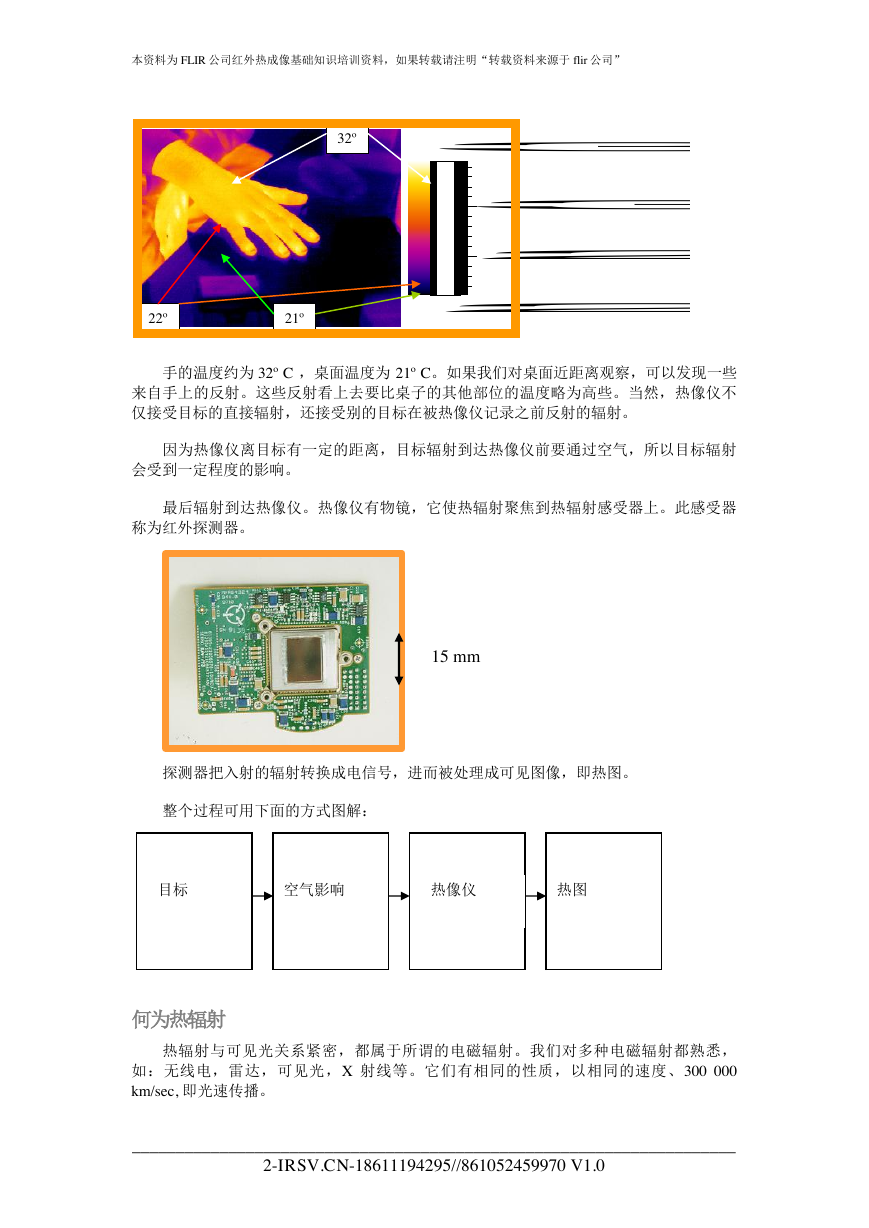
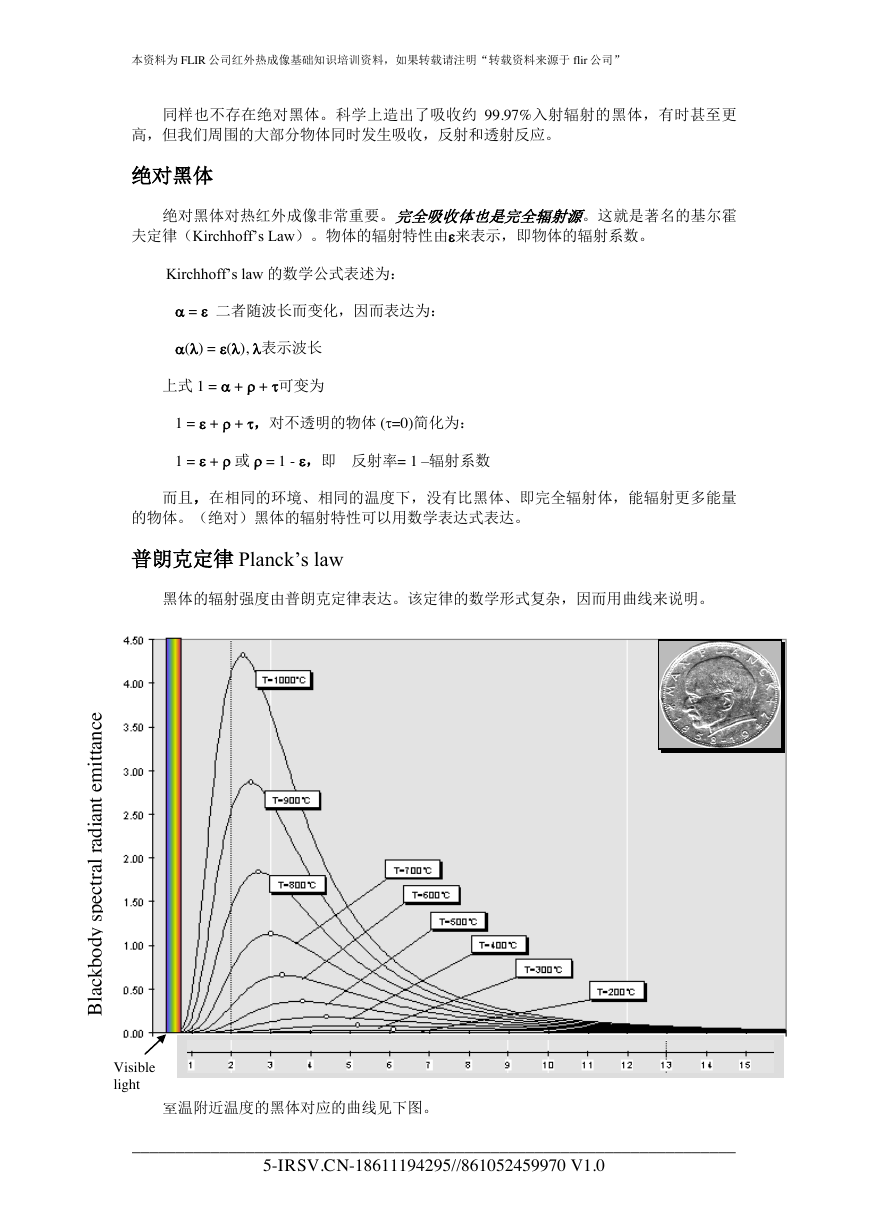
本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 32º 22º 21º 手的温度约为 32º C ，桌面温度为 21º C。如果我们对桌面近距离观察，可以发现一些来自手上的反射。这些反射看上去要比桌子的其他部位的温度略为高些。当然，热像仪不仅接受目标的直接辐射，还接受别的目标在被热像仪记录之前反射的辐射。因为热像仪离目标有一定的距离，目标辐射到达热像仪前要通过空气，所以目标辐射会受到一定程度的影响。最后辐射到达热像仪。热像仪有物镜，它使热辐射聚焦到热辐射感受器上。此感受器称为红外探测器。 15 mm 探测器把入射的辐射转换成电信号，进而被处理成可见图像，即热图。整个过程可用下面的方式图解：目标空气影响热像仪热图何为热辐射热辐射与可见光关系紧密，都属于所谓的电磁辐射。我们对多种电磁辐射都熟悉，如：无线电，雷达，可见光，X 射线等。它们有相同的性质，以相同的速度、300 000 km/sec, 即光速传播。 _____________________________________________________________________ 2-IRSV.CN-18611194295//861052459970 V1.0 21.1癈34.6癈2530

本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 不同的电磁波有各自不同的特性。因而，依据辐射的波长它们分成许多组。 The electromagnetic spectrum 红外线这个术语历史上源于这样一个事实，即红外光谱始于红色可见光的末尾处。热红外成像利用了红外光谱波段。短波的终点分界线位于可见光感知的极限，即深红处。长波段的终点，它在毫米波段融入微波无线电波。红外线波段一般分为四个子波段，它们分界线的选择有随意性，在各个国家略有不同。它们包括：近红外线中红外线远红外线极远红外线 0.75 – 3 µm 3 – 6 µm 6 – 15 µm 15 – 1000 µm “热”红外线是可以被热像仪感知、利用的红外线。波长大概介于 2 -- 13 µm 之间，这主要取决于探测器的类型。目标基础红外物理目前已经证实有一种不可见的辐射叫做红外辐射。这种辐射的性质和可见光的性质本质上相似。本章的目的是弄清楚该辐射的特性，目标如何发射该辐射，可能如何以不同的方式，数学的，图表的，来描述该辐射。所有物质以覆盖很宽波段的电磁波的形式辐射能量。辐射能量的强度很大程度上随波长而变化。如果目标很热，炽热，则很大一部分辐射以可见光的形式发射。如果目标温度低于约 500º C，则其辐射完全位于红外线波段。可见光辐射的能量强度太弱，人们感觉不到。物体不仅只发射辐射。所有物体都暴露在入射辐射中。这辐射可以是来自我们所关注的目标周围的任何物体。入射到目标的辐射受到目标的三个“反作用”。它可以被目标吸 _____________________________________________________________________ 3-IRSV.CN-18611194295//861052459970 V1.0

本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 收从而使目标升温；它能被目标反射；它还能穿过目标，即被目标透射。当目标透明时发生透射，如窗口，相机的光学部件等。入射辐射 W 吸收辐射 W 透射辐射 W 反射辐射 W 从此图导出下面的方程： W = W + W + W 简化为： 1 =  +  +  象大多数数学公式一样用希腊字母表示。这里 = alfa,  = ro ，  = tau。让我们来考虑一个目标。假如此目标的辐射特性可以用下面的式子来描述：  = 0 那么目标没有透射发生，它不透明。大多数物体如此。相对地，完全镜面反射所有的入射辐射，即：  = 1 这时既没有辐射被吸收也没有被透射，可得：  = 0 且  = 0 从而，对于一个完全镜面，下式成立：反射辐射 =入射辐射类似地，假设目标有如下性质：  = 0 且  = 0, 即：既无反射辐射也无透射辐射这个性质的结果是  = 1。这意味着入射辐射 100% 被吸收。此物体称为绝对黑体。绝对黑体吸收所有的入射辐射通常我们考虑的辐射是指可见光和红外线。在现实世界中没有完全透射，完全反射或完全吸收入射辐射的物体。这样的物体只存在于数学术语中。然而，有些物体在上述某方面非常近似于完全。有近似完全镜面，好的可以反射约 98%的入射辐射。为得到尽可能高的透射性能而设计的镜头对某一有限波段来说可透过高达 99%的入射辐射。 _____________________________________________________________________ 4-IRSV.CN-18611194295//861052459970 V1.0

本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 同样也不存在绝对黑体。科学上造出了吸收约 99.97%入射辐射的黑体，有时甚至更高，但我们周围的大部分物体同时发生吸收，反射和透射反应。绝对黑体绝对黑体对热红外成像非常重要。完全吸收体也是完全辐射源。这就是著名的基尔霍夫定律（Kirchhoff’s Law）。物体的辐射特性由来表示，即物体的辐射系数。 Kirchhoff’s law 的数学公式表述为：  =  二者随波长而变化，因而表达为： () = (), 表示波长上式 1 =  +  + 可变为 1 =  +  + ，对不透明的物体 (=0)简化为： 1 =  +  或  = 1 - ，即反射率= 1 –辐射系数而且，在相同的环境、相同的温度下，没有比黑体、即完全辐射体，能辐射更多能量的物体。（绝对）黑体的辐射特性可以用数学表达式表达。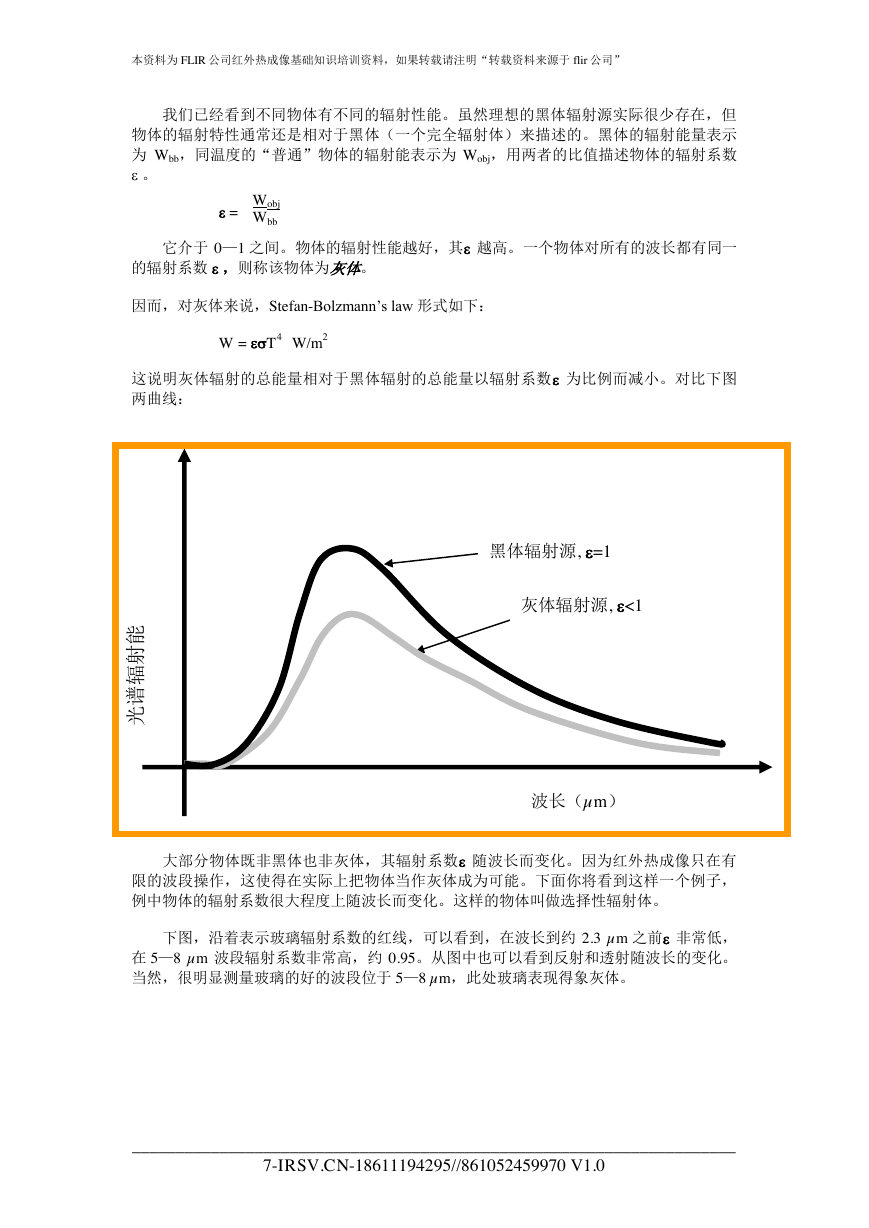普朗克定律 Planck’s law 黑体的辐射强度由普朗克定律表达。该定律的数学形式复杂，因而用曲线来说明。 e c n a t t i m e t n a i d a r l a r t c e p s y d o b k c a l B 该定律说明黑体每单位波长和波谱区域的辐射量——光波辐射量(W/m2x µm)。我们可以看到图中有几条曲线，每条曲线对应某一黑体温度，温度越高，辐射强度越强。 Visible light 室温附近温度的黑体对应的曲线见下图。 _____________________________________________________________________ 5-IRSV.CN-18611194295//861052459970 V1.0

本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 可以看到黑体辐射覆盖很宽的波谱，但它们有各自不同的辐射强度最大值。最大值处的波长可以计算出来。这公式就是著名的威恩位移定律，表达为 max = 2898/T T：物体的绝对温度，开氏温标测量 (K) max ：最大强度的波长 e c n a t t i m e t n a i d a r l a r t c e p s y d o b k c a l B e c n a t t i m e t n a i d a r e c n a t t i m e t n a i d a r y d o b k c a l b e 我们可以考虑的一个例子是太阳的温度。在其温度约为 6,000 K 时， max 将是 2898/6000  0.5 (µm)，碰巧在可见光波谱的中央，实际上这是人眼所感觉的最强的可见光。从表达普朗克定律的上面两图上可以看到 30º C 的物体辐射最强时的max 约为 10 µm，而 1000ºC 物体辐射最强时的max 约为 2.3 µm ，其强度为 30ºC 物体的 1,400 倍。相当大的辐射能量在可见光波段。史蒂芬-波尓兹曼定律（Stefan-Bolzmann’s law）从 Planck’s law 推导，物体总的辐出能量可以计算出来。此定律适用于黑体，形式如下： W = T4 W/m2  叫做 Stefan-Bolzmann 常数(5.67 x 10-8 W/m2K4)。一个例子是人类自身，温度为 300 K，每平方米面积辐射的能量约为 500 W 。人体的有效辐射面积约为 1 m2，因而它大约辐射 ½ kW 的能量——相当可观的热流失。辐射系数 _____________________________________________________________________ 6-IRSV.CN-18611194295//861052459970 V1.0

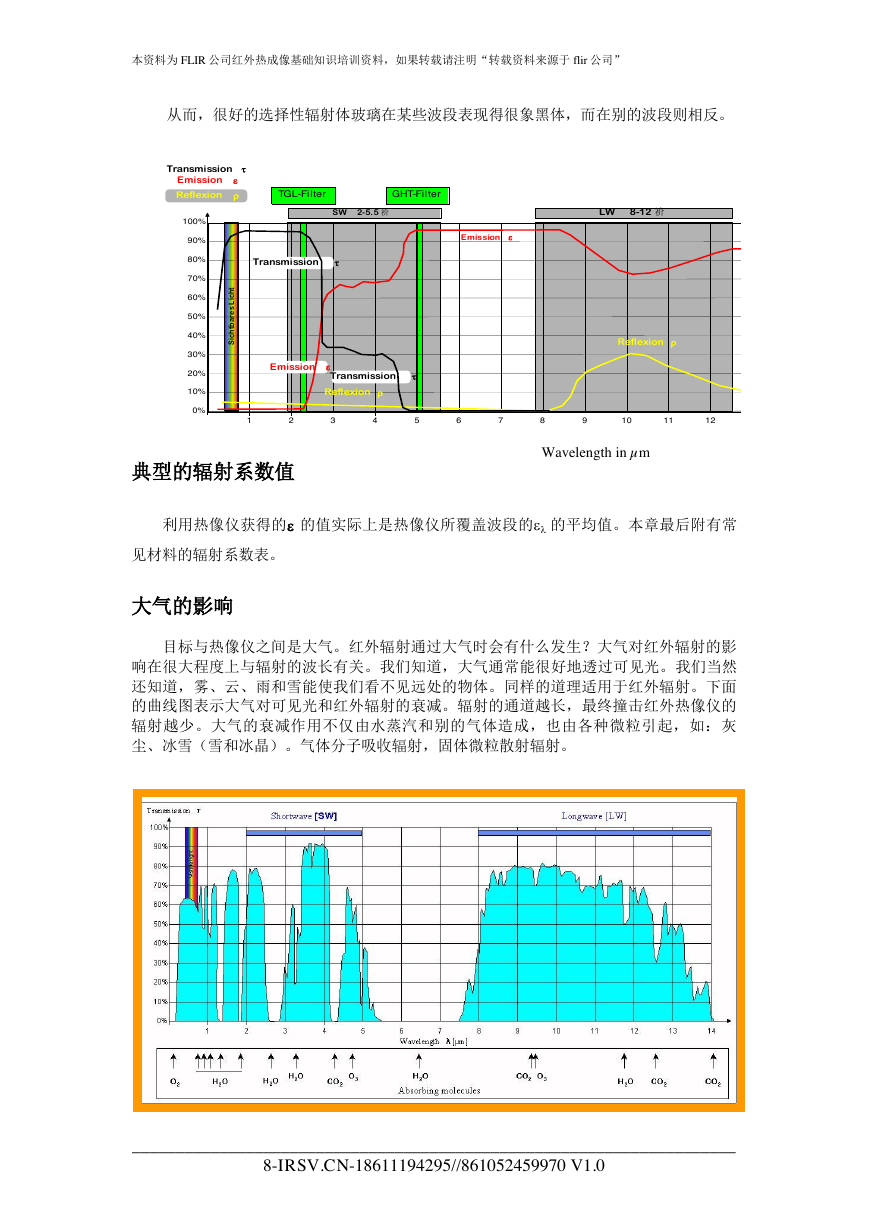
本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 我们已经看到不同物体有不同的辐射性能。虽然理想的黑体辐射源实际很少存在，但物体的辐射特性通常还是相对于黑体（一个完全辐射体）来描述的。黑体的辐射能量表示为 Wbb，同温度的“普通”物体的辐射能表示为 Wobj，用两者的比值描述物体的辐射系数  。它介于 0—1 之间。物体的辐射性能越好，其 越高。一个物体对所有的波长都有同一的辐射系数  ，则称该物体为灰体。  = Wobj Wbb obj 因而，对灰体来说，Stefan-Bolzmann’s law 形式如下： W = T4 W/m2 这说明灰体辐射的总能量相对于黑体辐射的总能量以辐射系数 为比例而减小。对比下图两曲线：能射辐谱光黑体辐射源, =1 灰体辐射源, <1 波长（µm）大部分物体既非黑体也非灰体，其辐射系数 随波长而变化。因为红外热成像只在有限的波段操作，这使得在实际上把物体当作灰体成为可能。下面你将看到这样一个例子，例中物体的辐射系数很大程度上随波长而变化。这样的物体叫做选择性辐射体。下图，沿着表示玻璃辐射系数的红线，可以看到，在波长到约 2.3 µm 之前 非常低，在 5—8 µm 波段辐射系数非常高，约 0.95。从图中也可以看到反射和透射随波长的变化。当然，很明显测量玻璃的好的波段位于 5—8 µm，此处玻璃表现得象灰体。 _____________________________________________________________________ 7-IRSV.CN-18611194295//861052459970 V1.0

本资料为 FLIR 公司红外热成像基础知识培训资料，如果转载请注明“转载资料来源于 flir 公司” 从而，很好的选择性辐射体玻璃在某些波段表现得很象黑体，而在别的波段则相反。 Wavelength in µm 典型的辐射系数值利用热像仪获得的 的值实际上是热像仪所覆盖波段的 的平均值。本章最后附有常见材料的辐射系数表。大气的影响目标与热像仪之间是大气。红外辐射通过大气时会有什么发生？大气对红外辐射的影响在很大程度上与辐射的波长有关。我们知道，大气通常能很好地透过可见光。我们当然还知道，雾、云、雨和雪能使我们看不见远处的物体。同样的道理适用于红外辐射。下面的曲线图表示大气对可见光和红外辐射的衰减。辐射的通道越长，最终撞击红外热像仪的辐射越少。大气的衰减作用不仅由水蒸汽和别的气体造成，也由各种微粒引起，如：灰尘、冰雪（雪和冰晶）。气体分子吸收辐射，固体微粒散射辐射。 _____________________________________________________________________ 8-IRSV.CN-18611194295//861052459970 V1.0 Sichtbares Licht234156710%20%30%40%50%60%70%80%90%100%Wellenl鋘ge  [祄]0%891011121413Reflexion 1516Transmission Emission Reflexion Transmission Emission Emission Transmission SW 2-5.5 祄LW 8-12 祄TGL-FilterGHT-FilterReflexion 

资料库

红外热成像基础知识.pdf

相关推荐

行业

热门标签

最新资料