总第 !" 卷 第 #!" 期 )**) 年 第 + 期 电测与仪表 ,&-./01.2& 3-2450-6-7/ 8 974/056-7/2/1%7 $%&’!" (%’#!" :5&’ )**) 基于 !"#$"% 中 &&’ 函数的电力谐波分析方法 李达义，陈乔夫，贾正春 ;华中科技大学电气与电子学院，武汉 #!**+#< 摘要：对电力系统谐波电压;或电流<进行了仔细分析，得出基于连续信号傅立叶级数的各 次谐波系数的计算公式，并推导了该计算公式与 32/&2= 函数 >>? 计算出的谐波系数的 关系。实例分析证明了基于连续信号傅立叶级数的谐波系数计算公式及其与 >>? 所计算 出系数关系的正确性。 关键词：谐波分析；>>?；32/&2= 中图分类号：?3"!!’# 文章编号：A**ABA!"*（)**)）*+B**)!B*# 文献标识码：@ (")*+,-. ","$/0-0 +1 2$2.#)-."$ 3+42) 0/0#2* %"025 +, !"#$"% （L.G%%& %I ,&-./01.2& ,7K17--017K M71N-041/E %I L.1-7.- 27O ?-.G%&%KE，P5G27 #!**+#，FG172） C1 D2E1，FG-7 H12%I5，:12 JG-7K.G57 6%0#)".#：?G- .500-7/;%0 N%&/2K-< %I -&-./01.2& Q%R-0 4E4/-6 14 272&ES-O 27O 2.G1-N- /G- /G- I57O26-7/2& 27O G206%71.4T RG1.G 14 2QQ&1-O /% 26Q&1/5O- .2&.5&2/17K I%065&24 %I .%6Q20- R1/G /G- .2&.5&2/17K 0-45&/4 %I %7- %I 32/&2=U4 I57./1%74B>>?T /G- 0-&2/1%7 %I /G- /R% 14 2.G1-N-O’ ?G- N2&1O1/E %I /G- 272&E414 14 Q0%N-O =E Q02./1.2& 2QQ&1.2/1%74’ 72/ 4+)50：G206%71. 272&E414；>>?；32/&2= 8 引 言 七十年代以来，各种电力电子装置在电力系统、 工业、交通和家用电器的广泛应用产生了大量的谐 波 ， 电 力 系 统 谐 波 已 经 成 为 电 力 系 统 的 一 大 公 害 VAW。为了治理电网中的谐波污染，首先要对谐波进 行测量，以便了解系统的谐波特征。在实际对非正弦 周期信号的测量中，一般都采用在一段连续时间内， 使电压（或电流）信号经过模数转换从而得到用有限 字长表示的离散时间信号，从中截取一个周期，来计 算出各次谐波的幅值。为了根据一个周期内离散序 式推导了采用 32/&2= 中的函数 >>? 计算出的系 数 与实际谐波系数的关系。 9 电力系统电压（或电流）傅立叶分析 设电力系统中电流、电压信号可用一个周期函 数来表示，即 !（"）X!（"Y#$） （A） 式中 $———周期函数的周期，且 #X*，A，)，!，……； !%A & $———代表电力系统的工频频率； !%’"!%)" & $ 为其相应的角频率。电力系统 中电流、电压信号一般都满足狄里赫利条件，因此可 列而计算出各次谐波的幅值，一种方法是基于连续 以分解成如下形式的傅立叶级数 信号的傅立叶级数的谐波分析方法：该方法根据连 续函数积分类比得到谐波系数计算公式，本文详细 Z !（"）X( *Y !（( ) .%4)!"Y*) 417)!"） ) X A 分析了这种情况下的各次谐波系数的计算公式；另 Z 一种是采用离散傅立叶变换，该方法根据数字信号 处理理论，直接采用 D>? 计算各次谐波 系 数 。 在 32/&2= 中也提供了一个函数 >>?，它同样可以进行 D>? 计算。遗憾的是，采用 D>? 计算出的系数并不 代表各次谐波真正的幅值V)W，为此，本文根据欧拉公 或 !（"）X( *Y ) X A !+) 417（)!",#) ） 其中 ( * X A $ $ *"!（"）O"X A )" " *"!（!"）O（!"） （)） （!） :;< < 

总第 !" 卷 第 #!" 期 )**) 年 第 + 期 电测与仪表 ,&-./01.2& 3-2450-6-7/ 8 974/056-7/2/1%7 $%&’!" (%’#!" :5&’ )**) ! " ; ) # ; = " ’" ; ) # ; = " # &" *!$（%）.%4"!%<% *! $（!%）.%4"!%<（!%） *!$（%）417"!%<% *! $（!%）417"!%<（!%） &" # ";=，)，!，… 比较式（)）和式（!），可以得出系数 ! " 、’" （#） 和 (" 之间的关系为 ) ) " (" ; ! " （?） >’" 式@)A中 第 一 项 ! * 为 函 数 $（%）的 直 流 分 量 ；第 二 项 (=417（!%)#= ）称为基波分量，其他各项为高次谐波。 式（#）的被积函数中，$（%）、.%4"!% 和 417"!% 都是以 # 为周期的连续时间函数，其中的积分上限或下限可 以根据需要任意给定，只要保持上、下限之间的差值 为一个周期即可。 ! 基于连续信号傅立叶级数的谐波分析 实际对非正弦周期信号的测量中，一般都没法 得到实际电压（或电流）的函数，各种录波装置记录 数据一般都不是连续的，而是在一段连续时间内，使 电压（或电流）信号经过模数转换并按一定频率来采 样得到用有限字长表示的离散时间信号。为了计算 出各次谐波的幅值，只需从采样序列中截取一个周 期就可以计算各次谐波的幅值。 下面推导了这种情况下的谐波系数。 设在一段连续时间内，对电压（或电流）进行均 匀采样得到了采样序列B$*C，从中取出一个周期 # 内 的 + 个点，记为 ，$) ，……，$+D= B$*C;$* ，$= 的可由式（#）按图 = 的积分累加和的方式类比计算 得到。此时若离散时间点为 %;* # @采样时间间隔 + A，在此离散时间点 $（%）的采样值为 $* ，则 <%; # + "!%,"- )" $ -* # + , &" # *"。 根据离散时间序列 $*# $的数据，可以由式（#）导 出计算第 " 次谐波的系数 ." 和 / " 的公式 ." , ) # , ) + / " , ) # +D= %$* .%4 )" + * , * +D= %$* .%4 )" + * , * +D= %$* 417 )" + * , * *"- # + *" *"- # + +D= , ) + %$* 417 )" + 其中 ";*，=，)，…，+D= 则第 " 次谐波的幅值 0 " * , * *" 为 （E） ) ) >/ " （+） " 0 "; ." 在 此 基 础 上 即 可 计 算 出 " 次 谐 波 电 压 含 有 率 @F206%71. G2/1% 3"A、" 次 谐 波 电 流 含 有 率 123" 124"@F206%71. G2/1% 4"AH!I 123"; 3" 3= 124", 4" 4= -=**J -=**J 式中 3" ———第 " 次谐波电压有效值（方均根值）； ———基波电压有效值； 3= ———第 " 次谐波电流有效值； 4" ———基波电流有效值。 4= 同理可以计算出电压谐波总畸变率 #156@/%/2& K206%71. <14/%0/1%7A和电流谐波总畸变率 #157 L #156; " ) %3" " ; ) 3= M=**J 图 = 累加和示意图 对于采样所得到的离散时间序列，其谐波系数 !*+ + L )" %4" " ; ) 4= #157; M=**J " 基于 #$%&$’ 函数 (() 的谐波分析 对于一个周期为 + 的离散的有限长序列 8@"A; 

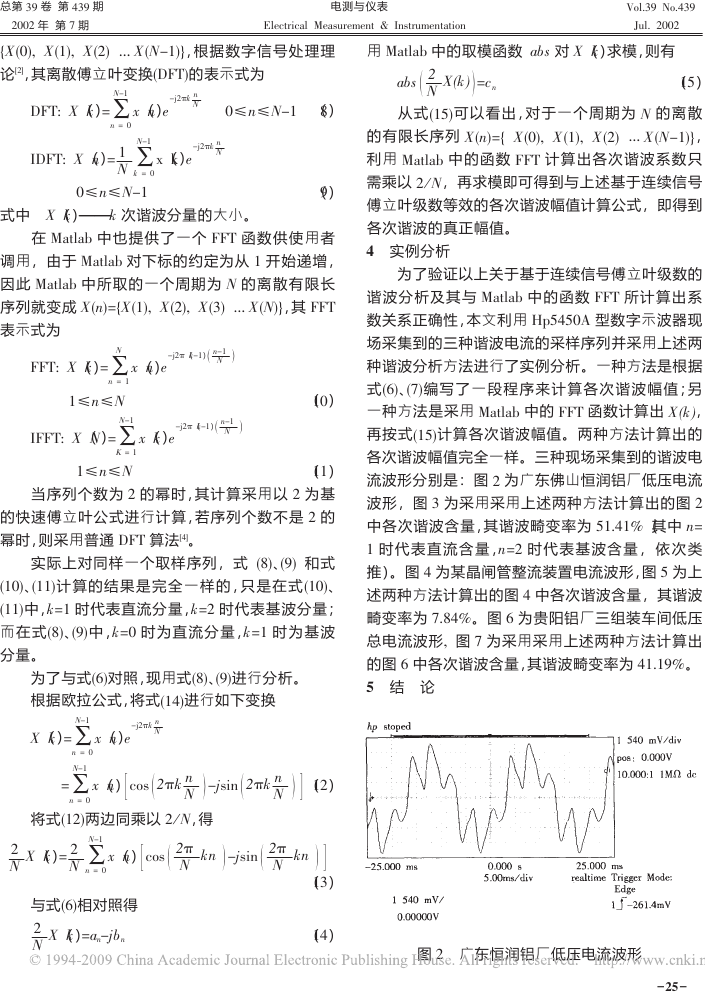
总第 !" 卷 第 #!" 期 )**) 年 第 + 期 电测与仪表 $%&’!" (%’#!" ,&-./01.2& 3-2450-6-7/ 8 974/056-7/2/1%7 :5&’ )**) 用 32/&2M 中的取模函数 ,-. 对 !（#）求模，则有 ;!<*=> ! !<)= …!<"@?=A，根据数字信号处理理 论B)C，其离散傅立叶变换 !<)=> ! ! !<)= …!<"@?=A， 利用 32/&2M 中的函数 EEF 计算出各次谐波系数 只 需乘以 ) O "，再求模即可得到与上述基于连续信号 傅立叶级数等效的各次谐波幅值计算公式，即得到 各次谐波的真正幅值。 # 实例分析 为了验证以上关于基于连续信号傅立叶级数的 谐波分析及其与 32/&2M 中的函数 EEF 所计算出 系 数关系正确性，本文利用 QRP#P*S 型数字示波器现 场采集到的三种谐波电流的采样序列并采用上述两 种谐波分析方法进行了实例分析。一种方法是根据 式 图 + 为采用采用上述两种方法计算出 的图 N 中各次谐波含量，其谐波畸变率为 #?’?"T。 " 结 论 "@? "% !%（$）.%4 )!# $ H & $ H * $’*417 )!# $ "" $ ’（?)） 将式

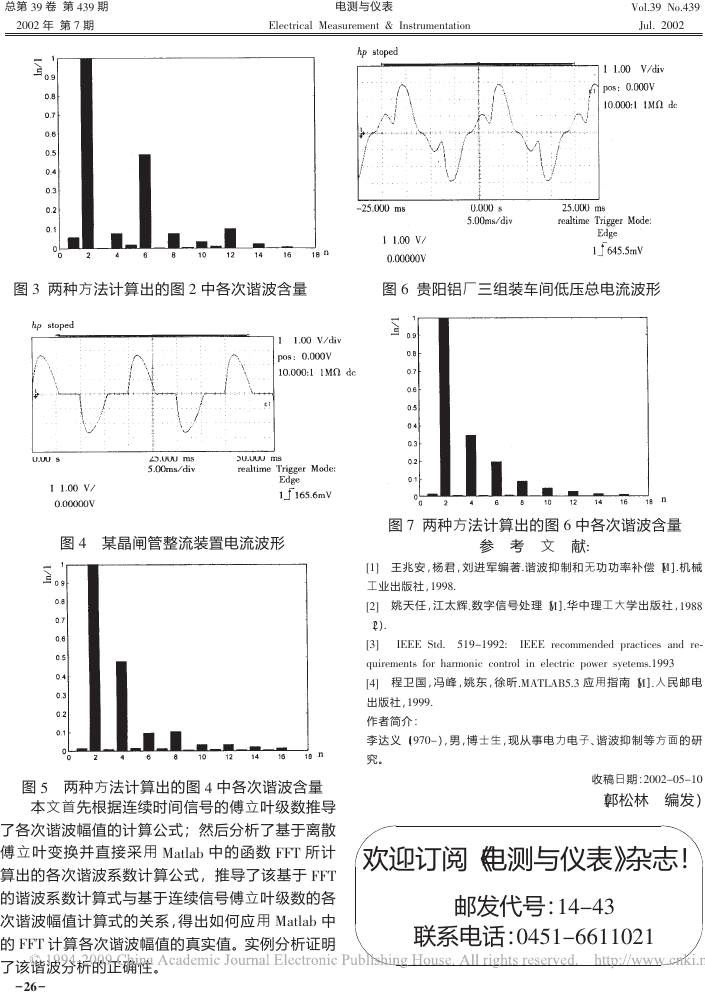
总第 !" 卷 第 #!" 期 )**) 年 第 + 期 电测与仪表 ,&-./01.2& 3-2450-6-7/ 8 974/056-7/2/1%7 $%&’!" (%’#!" :5&’ )**) 图 ! 两种方法计算出的图 ) 中各次谐波含量 图 ; 贵阳铝厂三组装车间低压总电流波形 图 # 某晶闸管整流装置电流波形 图 < 两种方法计算出的图 # 中各次谐波含量 本文首先根据连续时间信号的傅立叶级数推导 了各次谐波幅值的计算公式；然后分析了基于离散 傅立叶变换并直接采用 32/&2= 中的函数 >>? 所 计 算出的各次谐波系数计算公式，推导了该基于 >>? 的谐波系数计算式与基于连续信号傅立叶级数的各 次谐波幅值计算式的关系，得出如何应用 32/&2= 中 的 >>? 计算各次谐波幅值的真实值。实例分析证明 了该谐波分析的正确性。 # !" # 图 + 两种方法计算出的图 ; 中各次谐波含量 参 考 文 献@ ABC 王兆 安 ，杨 君 ，刘 进 军 编 著’谐 波 抑 制 和 无 功 功 率 补 偿 ［3］’机 械 工业出版社，B""D’ A)C 姚 天 任 ，江 太 辉’数 字 信 号 处 理 ［3］’华 中 理 工 大 学 出 版 社 ，B"DD （)）’ A!C 9,,, E/F’