旋转矩阵四元素法和光束法平差模型 1. 旋转矩阵的四元素表示法： 由于利用传统的旋转矩阵表示法解算时,旋转阵中的三角函数存在多值性和奇异性,经 常导致迭代计算的次数增加,甚至会出现不收敛的情况。Pope 从四维代数出发,提出用四个 代数参数 d, a, b, c 构成 R 矩阵,Hinsken 导出了一整套公式,即 pope-hinsken 算法(简称 P-H 算法),使 pope 参数在实际摄影测量中得到了应用。设四个参数 d, a, b, c 服从下列条 件（如式 3-1）: 2 2 cbad    2 12  ………………（式 3-1） 用这四个参数构造下列矩阵（如式 3-2）:  P d a b c 可以知道 P,Q 矩阵都是正交矩阵，从而可知（式 3-3）： b c d a  d a  b  c  c b  a d a d c  b       aQ              a  d c  b b  c d a  c  b  a d       …………（式 3-2） …………（式 3-3） T  PQ        因 T T  T T T PQ PQ I 4 X 4 可知 01 0 0 0 R T R 0 R 0       I 33 X , R 为正交矩阵，其形式如（式 3-4）： 上式就是旋转矩阵 R 的四元素表示法，可以表示任何一种旋转状态。 2. 光束法平差模型： 在解析摄影测量中，将外方位元素和模型点坐标的计算放在一个整体内进行，此时称其 为光束法。光束法平差是以共线方程式作为数学模型，像点的像平面坐标观测值是未知数的 非线性函数，经过线性化后按照最小二乘法原理进行计算。该计算也是在提供一个近似解的 基础上，逐次迭代来达到趋近于最佳值的。 ……（式 3-4） ①.共线方程式的表达： 设 S 为摄影中心，在世界坐标系下的坐标为（ SX , SZ ）;M 为空间一点，在世界坐 标系下的坐标为（X,Y,Z），m 是 M 在影像上的构象，其像平面和像空间辅助坐标分别为（x， y，-f），（ ），此时可知 S、m、M 三点共线。可得（式 3-5） ZYX mm SY , m , , Xm XS  X  Ym YS  Y  Zm ZS  Z  ……（式 3-5） 再根据像平面坐标和像空间辅助坐标的关系有（式 3-6） 

b 1 b 2 b 由式 3-5 和式 3-6 可解得共线方程式为（式 3-7） x y f  X Y m Z a 1 a a R                            m m T 3 3 2 c 1 c 2 c 3      *      m X Y m Z m      ……（式 3-6） x  x 0  y  y 0  (1 (3 af a af (2 a (3 X X   Xs Xs X X   Xs Xs b ) (1 Y  b ) (3 Y  b  b  ) ) (2 Y (3 Y YS  YS  YS  YS  c ) (1 ) ZS Z   c ) ) (3 Z ZS   c  c  ZS  ZS  (2 (3 Z Z ) ) ……（式 3-7） ) ) 其中， 0x 、 0y 、f 是影像内方位元素；表示像平面中心坐标和摄像机主距。 ②.共线方程式的线性化： F F  X  y 0 Xs X 该方程式一次项展开式为（式 3-8） d d   Fx Fx   Xs    Fy Fy   d d Xs    F F 0 y 式中 0XF 、 0yF 为共线方程函数近似值， Xsd 、 Ysd 、 Zsd 、 d 、 d 、 d 为外方位元素 d  Fx  Zs  Fy  d Zs  d  Fx  Ys  Fy  d Ys  d  Fx    Fy  d   d  Fx    Fy  d    Fx  X  Fy  X  Fx  Y  Fy  Y  Fx  Z  Fy  Z  d d d d …（式 3-8） d d            Xs   Ys Ys Zs Zs     X X Z Y Z Y 改正数， Xd 、 Yd 、 Zd 为待定点的坐标改正数。 在保证共线条件下有： , , Fx  X  Fy  X  Fx  Xs  Fy  Xs  Fx  Y  Fy  Y        此时，根据式 3-7 以及旋转矩阵可得到（式 3-10）：  1 a z Fx  Z  Fy  Z  Fx  Ys  Fy  Ys    Fx  Xs Fxa fa a   , , ) ( 1 z 12 11 3 1 a 13   Fx  Zs  a 22 Fy    Ys  1 z 1 z ( fc 1  c 3 Fx ) a 21 ( fb 2  Fyb 3 ) a 23 Fy    Zs  Fx  Zs  Fy  Zs  ( fb 1  Fxb 3 ) ( fa 2  Fya 3 ) ( fc 2  c 3 Fy )   Fx  Ys Fy    Xs  1 z 1 z f a 14   Fx    y sin   [ x f ( x cos   y sin )   cos  ] a 15 a 24   Fx   Fy      f sin   x f ( x sin   y cos )   x sin   [ y f ( x cos   y sin )   f sin cos a cos 16  ]   Fx    ……（式 3-9） ……（式 3-10） y a 25 Fy      f cos   y f ( x sin   y cos )  a 26 Fy      x ③误差方程式的建立： 据此可得到误差方程式为（式 3-11）： da  da  da da da da da da da da           26 25 24 23 14 22 16 15 13 12 Zs Ys Zs Ys   Xs Xs   X 11 da da 21 X   Y 12 da da 22 Y Z 13 da  da  23 x l  l  Z   …（式 3-11） y V X V y   11 da da 21 其中有： 

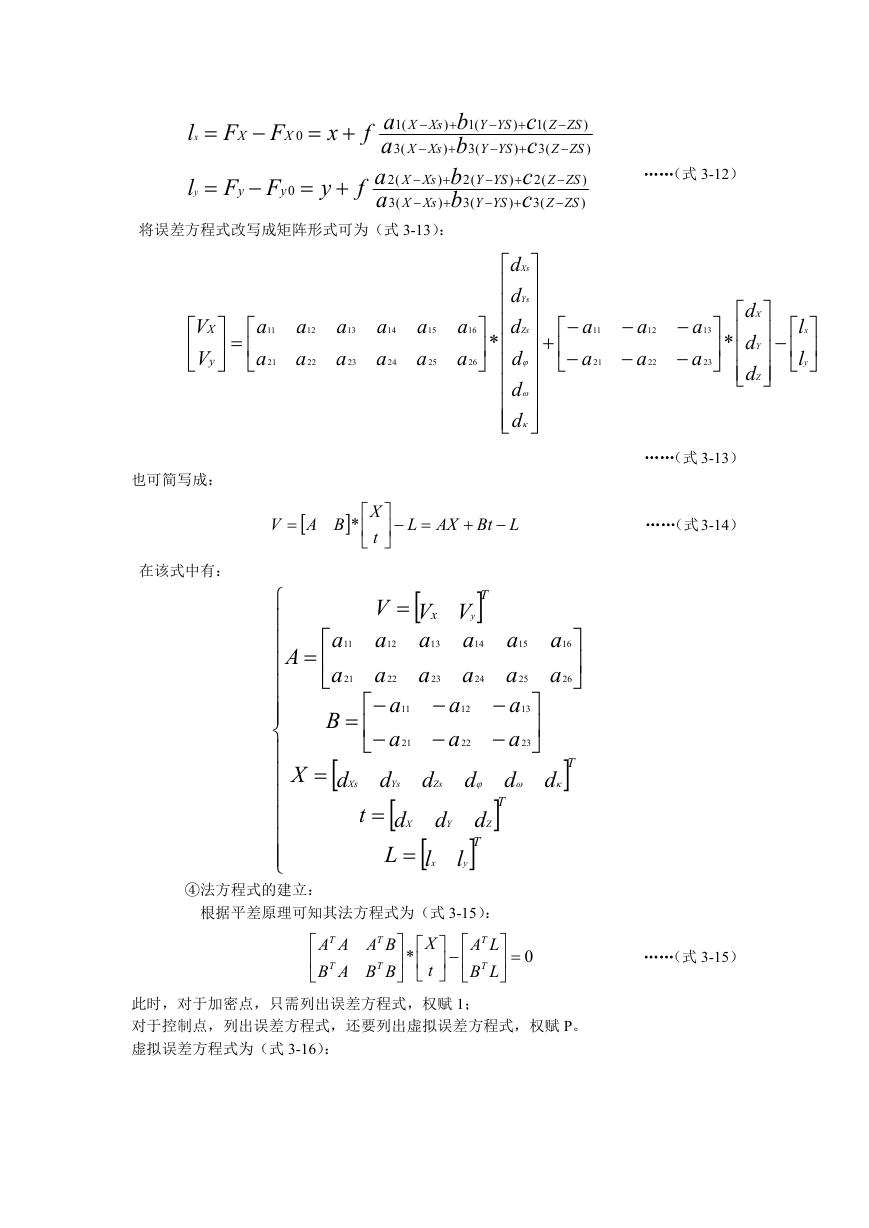
x 0 X X l x   F F  b (1 Y  b (3 Y  b (2 Y  b (3 Y  将误差方程式改写成矩阵形式可为（式 3-13）： af a af (2 a (3  Xs Xs Xs Xs (1 (3 F F X X   X X   y   ) ) ) ) l y 0 y y YS  YS  ) ) YS  YS  ) )   c ) (1 ZS Z   c ) (3 Z ZS   c (2 c (3 ZS  ZS  Z Z ) ) ……（式 3-12） V  X  V  y    a a    11 21 a a 12 22 a a 13 23 a a 14 24 a a 15 25 a a 16 26    *           d d d d d d Xs Ys Zs              也可简写成： 在该式中有： V   BA  * X t       L AX  Bt  L A  X  11 21 a a    B  d  Xs               11 12 22  V a a a  a  d   d L  21 Ys X    t y  VV x a a a a 23 13 T  14 24 a a 12 22   d Zs d Y l x  l  d d  T y Z 15 25 a a a  a  d T      13 23 d d d X Y Z       l   l  x y          a a 11 21   a a 12 22   a a 13 23    *      ……（式 3-13） ……（式 3-14） a a 16 26    T  d  ④法方程式的建立： 根据平差原理可知其法方程式为（式 3-15）：  T LA  T LB  T BAAA T BBAB    X t             * T T 0 ……（式 3-15） 此时，对于加密点，只需列出误差方程式，权赋 1； 对于控制点，列出误差方程式，还要列出虚拟误差方程式，权赋 P。 虚拟误差方程式为（式 3-16）： 

权为 P V   V   V  X Y Z X  Y  Z  ……（式 3-16） 列出各类点的误差方程式后，按照最小二乘法原理建立法方程式，即按 PVV 的法方程式为（式 3-17）： T PAA T PAB T PBA T PBB T PLA T PLB X t  0 *                   ……（式 3-17） 为最小建立 也可简写成：    N N 11 T 12 N N    12 22 * X t       L L 1 2       0 在根据上式进行展开消元可得改化法方程式为：  NNN  N  *  1  22 12 12 11 T LNNLX  1  12 22 1 2 ……（式 3-18） 或者  N  22 T NNN 1  12 11  t* 12  LNNL  1  12 11 T 2 1 ……（式 3-19） 根据式 3-18 可以求解出外方位元素的改正值；式 3-19 可以求解出点的坐标改正值。 ⑤.结果判定： 将改正数和规定的限差相比较，若小于限差则迭代完成，否则用未知数的新值又作为 近似值继续迭代，直至满足条件。 由此可知，开始时提供的初始值越接近最佳值，解的收敛速度就愈快；所以通常的处 理方法是先进行空间后方交会，求出像片的外方位元素，将其作为光束法平差时未知数的初 始值。 参考文献： 摄影测量学 武汉大学出版社 金为铣 2001 年 4 月 P23J1718