logo资料库

一个SPH流体实时模拟的全GPU实现框架.pdf

发布时间：2022-06-09 发布人：admin 分类：说明书 资料大小：1.32M 资料格式：pdf 举报 版权申诉
第1页 / 共9页
第2页 / 共9页
第3页 / 共9页
第4页 / 共9页
第5页 / 共9页
第6页 / 共9页
第7页 / 共9页
第8页 / 共9页
资料共9页，剩余部分请下载后查看
    引言
    相关工作
    拉格朗日流体模拟
    计算流体动力学和Navier-Stokes方程
    平滑粒子流体动力学（SPH）
    并行空间细分碰撞检测
    表面重构
    Marchingcubes（MC）算法
    基于几何着色器的MarchingCubes算法
    直方金字塔加速
    实验结果与对比分析
    结论
    一个SPH 流体实时模拟的全GPU 实现框架* 郭秋雷1, 唐逸之2, 刘诗秋3 , 李桂清4+ 1,2,4(华南理工大学计算机科学与工程学院, 广东省广州市 510006) 3(华南理工大学软件学院, 广东省广州市 510006) 摘摘摘摘 要要要要:::: 怎样实时地进行高度逼真的大规模流体模拟是图形学要研究的一个重要内容。流体的模拟由物理计 算、碰撞检测、表面重构和渲染几个部分组成，因此有大量工作针对流体模拟中的各个部分算法进行 GPU 加速。 本文提出一整套基于 GPU 的 SPH 流体模拟方案。我们在利用平滑粒子动力学（SPH）求解 Navier-Stokes 方程的 基础上，借助基于 GPU 的空间划分(Parallel Spatial Subdivision,PSS)策略来大幅度提升粒子碰撞的检测速度。同 时，设计了一种基于几何着色器(Geometry Shader)的流体表面信息的重建方法，并进一步的做了基于索引的优化， 使得表面重建过程无须遍历不包含表面的区域。实验结果表明，本文方法能实时模拟出具有较好真实感的流体场 景。 关键词关键词关键词关键词:::: 流体模拟;GPGPU;实时;SPH;并行空间划分;几何着色器;Marching Cubes 1111 引言 模拟流体方法大致可以分成两类：基于网格的欧拉方法和基于粒子的拉格朗日方法。欧拉方法主要跟踪 流体中固定的点，并把流动过的流体的速度，压力和密度等信息保存在这些固定的点中。这种方法的优势是 在固定的数据栅格中求解空间微分方程，因而相对容易，但缺点是容易导致流体的质量损失。拉格朗日方法[4] 则用大量离散的粒子去逼近流体的运动。每一个粒子保存有它本身的位置、压力、密度、速度等属性。利用 SPH 以及平滑核来计算粒子间的相互作用[4]，从而更新流体的运动状态。 本文把并行空间划分(Parallel Spatial Subdivision, PSS)方法[11]引入基于 SPH 粒子计算中，判断粒子间的 相互碰撞及作用。具体地，将流体空间划分为若干个网格，并对每一个网格中存在的粒子计算出一个索引， 通过这个索引可以迅速地定位所有可能的碰撞粒子对，实现高效的碰撞检测。 拉格朗日方法只能得到流体中离散的粒子属性信息，想要在屏幕中渲染出流体，还需要流体表面的几何 信息。本文采用经典的 Marching Cube（MC）算法来重构流体表面。由于需要遍历所有体素，Marching Cube 算法通常要耗费大量的时间处理表面无关的体素。此外，如果在 CPU 中重构，则绘制时需要在 CPU 和 GPU 之间耗费大量的吞吐量来传输计算出来的定点数据。本文设计了一个基于几何着色器(Geometry Shader)的 MC 实现，利用硬件加速曲面的生成，避免了管线各阶段之间的数据的吞吐量。同时我们对 MC 作了优化：运用 直方金字塔方法在粒子运动模拟阶段记录了流体中表面位置的索引。在 MC 阶段，只对流体中包含表面的网 格进行表面重建，极大提高了算法模拟的效率。本文的主要贡献可归结为：利用最新的 GPU 加速技术设计了 一个流体模拟的 GPU 实现框架；提出一个基于几何着色器的 Marching Cube 加速算法。 * Supported by the NSFC(No. 60973084), 国家自然科学基金; NSF of Guangdong(No. 915106410-1000106), 广东省自然科学基金; and Fundamental Research Funds for the Central Universities (2009 zz0016), 中央高校基金. 作者简介：郭秋雷(1987-),男,广东湛江人,硕士研究生,主要研究领域为物理模拟,GPGPU 计算;唐逸之(1990-)，男，本科生， 湖南邵阳人，主要研究领域为图形学；刘诗秋(1989-),男，湖北武汉人，本科生，研究领域为图形学，人工智能;李桂清(1966-), 男,教授,论文通讯作者，主要研究领域为 CAGD, DGP, RE,复杂物体的几何造型, Phn:13672400186,E-mail: ligq@scut.edu.cn;
    2222 相关工作 Müller 等[4]提出了一种基于平滑粒子动力学(SPH)的粒子来模拟流体的运动。其主要贡献是提出用于对 应密度、粘度、速度的计算 SPH 平滑核。随着 GPU 硬件以及可编程管线的发展, 利用 GPU 的大规模并行运 算能力求解流体方程已经非常常见. 文献[1]首先提出了用 GPU 并行求解的方法。Fedkiw 等[9]提出一种改进 的基于欧拉迭代的网格算法，可以渲染出网格精度非常高 (512 512 512)、真实感很强的流体场景，只是这 种方法还只能适用于离线渲染。 拉格朗日方法的思想是用大量粒子来模拟流体的运动，而处理大量粒子之间的相互碰撞等作用是个很耗 时的问题，为此文献[14]指出两种大规模碰撞检测的加速思路：即层次包围体(BVH)和空间划分(SP)。文献[11] 进一步提出了基于 CUDA 的空间划分，使得大规模的粒子物体的相互碰撞得以在 GPU 上并行化。 在曲面重建方面，最经典如 Marching Cube [6]，虽然能对给定的标量场中生成具有较高精度的三角网格 等值曲面，但这些方法效率较低。文献[10]提出一种新颖的基于点的曲面重建方法. 文献[8]则在提出一种在 屏幕空间渲染出流体曲面的方法，避免了传统 Marching Cube 的运算开销。但是这类方法得出的流体表面较 之 Marching Cube 方法的误差要大。为此本文提出一个基于几何着色器的 Marching Cube GPU 加速方法，利 用 Dyken 等人的直方金字塔技术[12]对其进一步加速，以便更好地满足了等值曲面的逼近精度和算法的实时 性要求。 3333 拉格朗日流体模拟 我们先在 3.1 节介绍 Navier-Stokes 方程来对流体进行物理建模，然后在 3.2 节里阐释用平滑粒子流体动 力学方法 SPH (Smoothed Particle Hydrodynamics)来模拟任意表面的流体。 3.13.13.13.1 计算流体动力学和Navier-Stokes方程 我们主要根据 Navier-Stokes 方程[4]来对流体进行建模，它是计算流体动力学的基础。下面的 Navier-Stokes 方程是应用于抗压缩流体一个版本 ⎛ ρ ⎜ ⎝ v ∂ t ∂ ⎞ vv ∇⋅+ −∇=⎟ ⎠ gp 2µρ ∇+ + . v (1) 方程(1)中, g表示外力密度场，一般是重力密度场， µ是流体的粘性系数，v是速度场，p是压力密度场， ρ 表示密度。方程右边分别给出了粒子受到的压力、外力、粘力这三项；而左边则表示每个 SPH 粒子受到的合 力 ( 3.23.23.23.2 平滑粒子流体动力学（SPH） )vvtv ∇⋅+∂∂ρ 。 平滑粒子流体动力学方法 SPH (Smoothed Particle Hydrodynamics)是近二十多年来逐步发展起来的一种无 网格方法，原本是由 Lucy 和 Gingold 开发用于研究天体物理问题，不过它也可用于各种形式的流体模拟[4]。 SPH 的核心是插值计算，插值的形式如下 )hrrWAmrA ,− j ( ) ( S ∑= j j j ρ j . (2) 公式(2)中, j表示在所有的粒子上扫描遍历; A表示某种属性值，如密度、力等， jA表示粒子 j的这种属性值; rj 、 mj 和 ρj 分别表示粒子 j的位置、质量和密度; r表示空间中某个位置，和 rj 一样可以看作 3D 向量， ( )rAS 表 irr− 是一个向量，第二个 示位置为 r的地方的 A的属性值;W称为平滑核，它是一个二元函数，第一个参数 参数 h是一个常实数[4]。
    作者名 等:题目 4444 并行空间细分碰撞检测 3 由于 SPH 思想的核心是插值计算，所以我们必须计算周围粒子对相应粒子的作用力。简单地暴力遍历所 ( 2nO 。当流体规模增大，粒子数目急速增加的时候流体渲染的效率会大大降低。为 有粒子的时间复杂度为 此我们采用了[11]中提出的基于 GPU 的并行空间细分碰撞检测方法。下面描述算法的思路并指出本文优化的 地方，具体的实现细节可以参考[11]。 ) 该方法的核心内容是将空间划分成统一均匀的网格，来充分发挥 GPU 的并行能力。每个网格的大小至少 大于等于场景中最大的粒子（物体）。这样每个物体最多只能与 dim2 个网格相交（dim 为场景的维数）。然后通 过如下的 Hash 映射[11][16]，求得每个粒子与它所相交网格的 Hash 值，并存到一个 cell id 数组: zS |) cSzpos xpos / pId ((= xS / . . . *) yS ((|) hash cSize *) cSize *) ((|) pos是粒子的位置，cSize是网格的大小， zSySxS , , ypos / (3) 分别是 hash 映射时的偏移量， pId是粒子的序号。 文献[11]中将粒子与每个它有相交的网格都建立了一个 hash 值，这样可以快速准确地定位发生碰撞的粒子对。 但也有它的局限性，一是会导致构造碰撞对的时间开销增加，二是只能采用稳定的排序算法对上面的 hash 值 进行排序。我们采用了[16]中"loose grid"的做法，只对粒子与它中心所在的网格建立 hash 值，这样节省了构 造的时间, 确定与当前粒子发生碰撞的粒子时，也只是需要遍历与当前粒子中心所在的网格相邻的 dim2 网格。 虽然遍历会多花了一点时间，但是这样算法实现的会更加地简单。而且对上面 hash 值排序时也无需稳定的排 序算法。从经验来看这样的速度会更加快[16]。Algorithm 1 给出了我们的基于 GPU 的并行空间划分算法的伪 代码描述。 Algorithm 1 Parallel Spatial Subdivision 1）根据 eq4.1 计算每个粒子与它中心所在网格的 hash 值； 2）对上面得到的 hash 值进行排序(可以采用基于 GPU 的双调排序)； 3）根据排序的结果，得到每个网格里面所有的粒子； 4）每个粒子分配给一个 GPU 线程，遍历所有粒子； 5）计算粒子所在的网格； 6）遍历当前网格和相邻的 dim2 个网格里面的粒子，看是否发生碰撞； 7）如果发生碰撞则根据 e.q3.1 和 e.q3.2 来对当前粒子的受力进行更新； 5555 表面重构 通过前面的物理模型及碰撞检测方法，可以计算出每个时间片 SPH 粒子在空间中的位置，流体的表面就 可以重构出来。我们使用 Marching Cubes 的思想[6]来做表面重构。 5.15.15.15.1 Marching cubes（MC）算法 Marching Cubes 算法的基本思想是：已知空间的一个数据场，并给出一个期望的数据值，以确定要重构 的等值面。将空间划分成小立方体网格(Cubes)，计算 cube 的顶点数据值。顶点数据值大于期望数据值标记 成 1，小于标记成 0。每个 Cube 有 8 个顶点所以，共有 256 种情况，即 cube 可以做 256 个分类。根据每个 cube 的分类和一张预定义的三角形链接表从每个 cube 中提取出插值三角形，最终得到表示等值面的三角网 格。 在实际应用中，有时还需要直接根据体数据估计顶点的法向，以便得动更好的渲染效果。三角形的顶点 位置是通过在 cube 的边上插值计算得出的，法向同样也要通过插值来计算。因此，事先不仅要计算 cube 的 顶点数据，还要计算 cube 的顶点法向。幸运的是，文献[6]给出了的一个很简单的计算顶点法向的方法，即 中点差分法。
    5.25.25.25.2 基于几何着色器的Marching Cubes算法 CPU 负担很大的计算量，且消耗大量的内存。 传统的 Marching Cubes 实现大多是基于 CPU[7]，这样效率会很低，原因如下: � 数据需要在显存和内存之间不断传输，传输速度很慢。 � 占用大量 IO 带宽。 � 为了解决这个问题[3]曾提出了一种在顶点着色器(VertexShader)上实现的 MarchingCube。顶点着色器是 专门处理顶点的 GPU 渲染管道（shader），但其每次运行只能处理一个顶点的数据。在绘制的几何图形的任务 量非常庞大时，如果仅依靠顶点着色器来完成，效率会极其低下。而几何着色器 GeometryShader 是 Shader Model 4 引进的新的着色器，专门用来加速处理场景中包括三角形在内的几何图形。为此本文设计了一种基 于 GPU 几何着色器的 Marching Cubes 实现方案。 关于几何着色器实现 Marching Cubes 的具体流程如下 Geometry shader Vertex shader Pixel shader Cube index Triangle 1. 2. 3. 4. 5. 6. 7. 根据输入的 cube 索引确定当前要处理的 cube 获取当前 cube 的 8 个顶点数据 根据 8 个顶点数据对 cube 分类 如果 cube 与等值面不相交，就结束整个流程（不进入 Pixel shader），否则继续第 5 步 插值计算 12 条边与等值面的交点 根据 cube 分类对应的三角链接表将交点连接成三角形 进入 Pixel shader 图 1 几何着色器实现 MC 算法的流程 从上面的流程图可以看到，每个 cube 都需要一个几何着色器来处理。顶点着色器输出的其实是表示 cube 的索引。虽然顶点着色器的输出通常是一个顶点，也就是一个 3D 浮点向量，但是这个向量同样也可以表示 一个 3D 的索引。根据空间划分 Cube 的方法，cube 在空间中就是一种 3D 的分布，所以自然可以用 3D 向量 作索引。 5.35.35.35.3 直方金字塔加速 每个 cube 都需要启动一个几何着色器来处理。在高精度 MC 算法，由于 cube 数量很大，这必然会消耗 一定的时间。在算法流程中，我们就发现有一些 cube 中没有三角形生成，所以这里启动的几何着色器白白浪 费了。如果能够剔除这些无用的 cube，并且只启动有三角形生成的 cube 所对应的几何着色器，这样便能大 大提高 MC 算法的效率。我们采用了[12]提出了一种“直方金字塔”的方法解决这一问题。 该方法首先并行计算出一个“直方金字塔结构”，在该结构上可按顺序快速遍历有效 cube 的索引。我们 只需在顶点着色器中计算出有效 cube 的索引，并将该索引输出给几何着色器即可实现加速。下面，我们以一 维直方金字塔为例介绍这种加速方法。
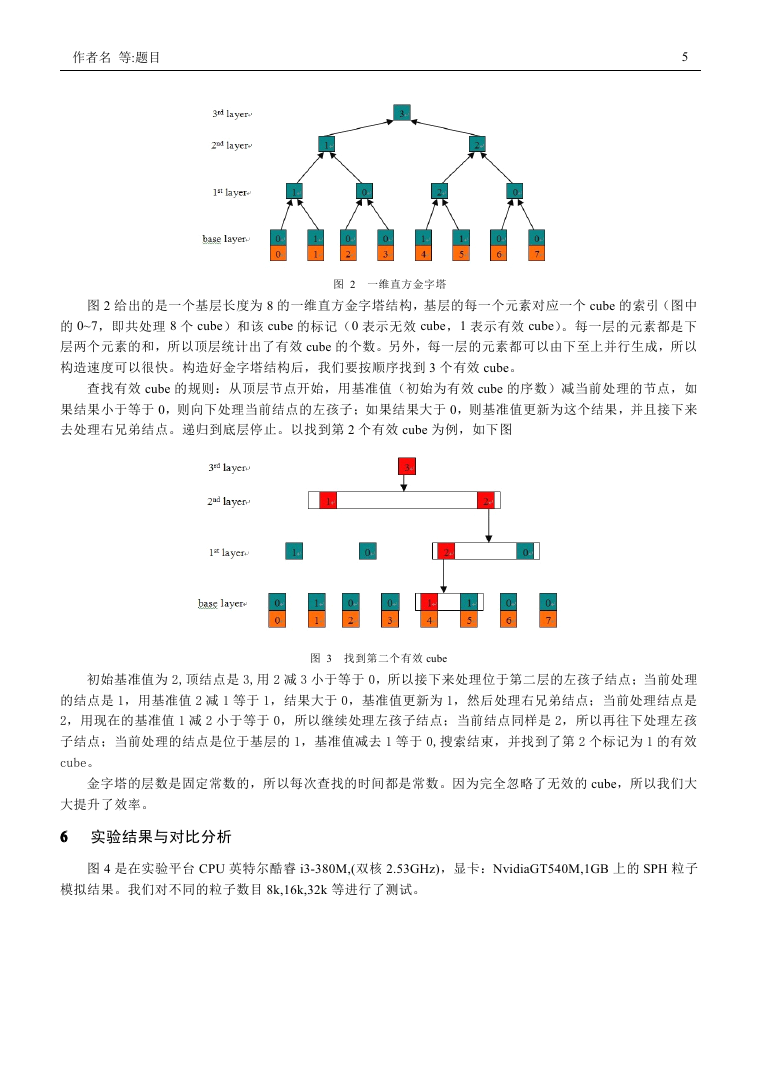
    作者名 等:题目 5 图 2 一维直方金字塔 图 2 给出的是一个基层长度为 8 的一维直方金字塔结构，基层的每一个元素对应一个 cube 的索引（图中 的 0~7，即共处理 8 个 cube）和该 cube 的标记（0 表示无效 cube，1 表示有效 cube）。每一层的元素都是下 层两个元素的和，所以顶层统计出了有效 cube 的个数。另外，每一层的元素都可以由下至上并行生成，所以 构造速度可以很快。构造好金字塔结构后，我们要按顺序找到 3 个有效 cube。 查找有效 cube 的规则：从顶层节点开始，用基准值（初始为有效 cube 的序数）减当前处理的节点，如 果结果小于等于 0，则向下处理当前结点的左孩子；如果结果大于 0，则基准值更新为这个结果，并且接下来 去处理右兄弟结点。递归到底层停止。以找到第 2 个有效 cube 为例，如下图 图 3 找到第二个有效 cube 初始基准值为 2,顶结点是 3,用 2 减 3 小于等于 0，所以接下来处理位于第二层的左孩子结点；当前处理 的结点是 1，用基准值 2 减 1 等于 1，结果大于 0，基准值更新为 1，然后处理右兄弟结点；当前处理结点是 2，用现在的基准值 1 减 2 小于等于 0，所以继续处理左孩子结点；当前结点同样是 2，所以再往下处理左孩 子结点；当前处理的结点是位于基层的 1，基准值减去 1 等于 0,搜索结束，并找到了第 2 个标记为 1 的有效 cube。 金字塔的层数是固定常数的，所以每次查找的时间都是常数。因为完全忽略了无效的 cube，所以我们大 大提升了效率。 6666 实验结果与对比分析 图 4 是在实验平台 CPU 英特尔酷睿 i3-380M,(双核 2.53GHz)，显卡：NvidiaGT540M,1GB 上的 SPH 粒子 模拟结果。我们对不同的粒子数目 8k,16k,32k 等进行了测试。
    图 4 8K，16K，64K 粒子效果 图 5 给出在只绘制粒子时，采用了我们的 GPU 并行空间划分加速和暴力算法两种情况下，平均帧速和粒 子数目的关系. 可以看到 GPU 并行空间划分加速算法加速的效果很明显，对于 8K 的粒子，加速效果甚至达 到 20 倍。 ） s p f 位 单 （ 速 帧 2 0 0 1 5 0 1 0 0 5 0 0 帧 速 随 粒 子 数 目 的 变 化 （ 只 绘 制 粒 子 ） 1 8 2 . 8 3 8 2 . 2 8 加 速 后 加 速 前 0 9 . 6 1 0 2 . 5 2 0 4 1 . 2 8 0 . 6 3 3 0 4 0 5 0 6 0 2 0 . 0 7 0 7 0 粒 子 数 目 （ 单 位 K = 1 0 2 4 ） 图 5 帧速随粒子数目变化（只绘制粒子） 图 6 给出了 2 幅是我们绘制流体表面的效果，采用的 Marching Cubes 体素的精度是 50×50×50。 图 7 表示绘制流体表面时（Marching Cubes 体素 50×50×50），使用了加速的情况下，平均帧速和粒子 图 6 32K，64K 粒子绘制表面的效果 数目的关系 ） s p f 位 单 （ 速 帧 1 0 0 8 0 6 0 4 0 2 0 0 帧 速 随 粒 子 数 目 的 变 化 （ 绘 制 表 面 ） 8 1 . 5 3 4 3 . 8 9 2 3 . 9 3 1 4 . 9 6 加 速 后 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 粒 子 数 目 （ 单 位 K = 1 0 2 4 ） 图 7 帧速随粒子数目变化（绘制表面） 接下来我们看看 Marching Cube 的体素大小对我们帧速的影响。这次我们采用的平台为 CPU 英特尔酷睿 i5-760,双核 2.80GHz)，显卡：Nvidia Geforce GTX460。图 8 表示 32k 个 SPH 粒子，在 Marching Cube 的体素
    作者名 等:题目 数为 50-80 的情况下，帧速的变化。 7 图 8 帧速随 Marching Cube 体素大小的变化 Takashi Amada 在[15]中实现了一个基于 GPU 的 SPH 流体模拟算法，在 Intel Core i5-760 CPU, 双核 2.80GHz), Nvidia Geforce GTX460 GPU 平台下，对于 2k 个粒子的模型，在绘制流体表面时，帧速最多只能达 到 16.5fps。文献[17]也实现了一个基于 SPH 方法的二维流体实时模拟, 运行于 Intel Core2 Duo E8400 3.0G CPU, Geforce 8800 GT GPU 的平台上，在只绘制粒子的情况下， 3k 粒子只有 20fps。文献[5]在[16]工作基础 上，重构流体表面，运行 Intel Xeon 3.7GHz CPU, Geforce 8800 ULTRA (768MB)平台，32k 粒子速率为 50fps。 由此可见我们的加速方案很成功，分别比[15], [17]快了几十倍不等。排除平台性能在 Marching Cube 的体素 数较少的情况下我们也优于[5]。 7777 结论 可以看到我们成功地提供了一套完全基于 GPU 的实时 SPH 流体渲染方案，实现了 SPH 流体的实时模拟。 我们所有的计算都在 GPU 上进行，免去了 CPU 和 GPU 之间的大量 IO 时间。而且我们分别在粒子相互碰撞 上采用了并行空间细分思路，和在表面重构上实现了基于几何着色器的 Marching Cube，以及用直方金字塔索 引剔除无用的 cube。这都大大提高了我们流体模拟的速度，成功达到了实时渲染的要求。但由于碰撞时我们 只考虑到 SPH 粒子，所以接下来我们可以考虑扩展我们的模型，使之能够处理流体与任意场景，物体的交互。 参考文献 [1] Mark J. Harris. Fast fluid dynamics simulation on the GPU. In GPU Gems, 2004, 637-55. [2] Michael Kass and Gavin Miller .Stable fluid dynamics for Computer Graphics. ACM SIGGRAPH 1990, 49-57. [3] Frank Goetz,Theodor Junklewitz and Gitta Domik. Real-time marching cubes on the vertex shader. In Eurogrsphics 2005 Short Presentaions. [4] Matthias Müller, David Charypar and Markus Gross. Particle-based fluid simulation for interactive applications. In Proceedings of ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, 2003.154-159. [5] Kun Zhou, Minmin Gong, Xin Huang, Baining Guo. Data-parallel octrees for surface reconstruction. IEEE Transactions on Visualization & Computer Graphics, 2010, to appear. [6] William E. Lorensen , Harvey E. Cline. Marching Cubes: A High Resolution 3D Surface Construction Algorithm. SIGGRAPH 87 Conference Proceedings, 1987, 21(4), 163-170. [7] Paul Bourke. Polygonising a scalar field. http://paulbourke.net/geometry/polygonise/ [8] Simon Green. Screen space fluid rendering for games. In Proceedings for the Game Developers Conference, 2010. [9] Michael Lentine, Wen Zheng,Ronald Fedkiw. A novel algorithm for incompressible flow using only a coarse grid projection.
    SIGGRAPH 2010 papers,2010.1-9.2. [10]Kees van Kooten, Gino van den Bergen, Alex Telea. Point-based visualization of metaballs on a GPU. In GPU GEMS 3, 2007.123-149. [11]Scott Le Grand. Broad-phase collision detection with CUDA. In GPU GEMS 3, 2007.697-721. [12]Christopher Dyken, Gernot Ziegler. Highspeed marching cubes using histogram pyramids. Computer Graphics Forum, 27(8), 2008. 2028–2039. [13] J. P. Morris. Simulating surface tension with smoothed particle hydrodynamics. International Journal for Numerical Methods in Fluids, 2000, 33(3):333-353. [14]Christer Ericson. Real-time Collision Detection. Morgan Kaufmann, 2004. [15]Takashi Amada. Real-time particle-based fluid simulation with rigid body interaction. Game Gems 6, Charles River Media, 2006, 189-206. [16]Simon Green. Particle simulation using CUDA. In Nvidia CUDA sdk 4.0, 2010, http://developer.nvidia.com/cuda-downloads. [17]常元章，鲍凯，朱鉴，吴恩华.基于 SPH 方法的二维流体实时模拟.全国第 16 届计算机辅助设计与图形学学术会议, 2010, 山 西太原，264-270. Framework Rendering Real-time SPHSPHSPHSPH FluidFluidFluidFluid Rendering Real-time AAAA Real-time Framework OnOnOnOn TheTheTheThe GPUGPUGPUGPU Real-time Rendering Framework Rendering Framework Qiulei Guo1, Yizhi Tang2, Shiqiu Liu3 , Guiqing Li4+ 1, 2, 4(Department of Computer Science and Engineering, South China University of Technology, GuangZhou 510006, China) 3(Department of Sofware, South China University of Technology, GuangZhou 510006, China) + GuiQing Li: E-mail: ligq@scut.edu.cn fluid simulation ofofofof fluid simulation Real-time Abstract Abstract Real-time simulation fluid Abstract Real-time simulation Abstract: Real-time fluid is a great challenge in computer graphics. It consists of fluid dynamics, collision detection and surface reconstruction. A lot of GPU-based algorithms accelerating each stage of the problem. This paper proposes a GPU based framework for fluid rendering which can achieve real-time performance for medium scale fluid simulation.The approach employs hydrodynamics to solve Navier-Stokes equation. Collision detection is sped up using a parallel spatial subdivision strategy in this stage. The marching cube approach is employed to extract isosurfaces of the fluid using geometry shader. This stage is further optimized with histogram pyramids so that we don't have to travel those empty areas. Experimental results show that our framework is very fast and able to achieve KeyKeyKeyKey words words words words: Fluid Rendering;GPGPU;SPH;Real-time;Parallel Spatial Subdivision;Geometry Shader;Marching Cube real-time performance perfectly. have been brought forward for smoothed particle
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料