logo资料库

水箱液位控制系统设计.doc

发布时间：2022-06-10 发布人：admin 分类：说明书 资料大小：0.18M 资料格式：doc 举报 版权申诉
第1页 / 共7页
第2页 / 共7页
第3页 / 共7页
第4页 / 共7页
第5页 / 共7页
第6页 / 共7页
第7页 / 共7页
资料共7页，全文预览结束
    一、模糊控制系统的结构
    二、利用MATLAB对水箱水位系统进行仿真建模
    （一）水箱水位模糊推理系统（FIS）的建立
    （二）对SIMULINK模型控制系统的构建
    （三）进行Simulink模型仿真
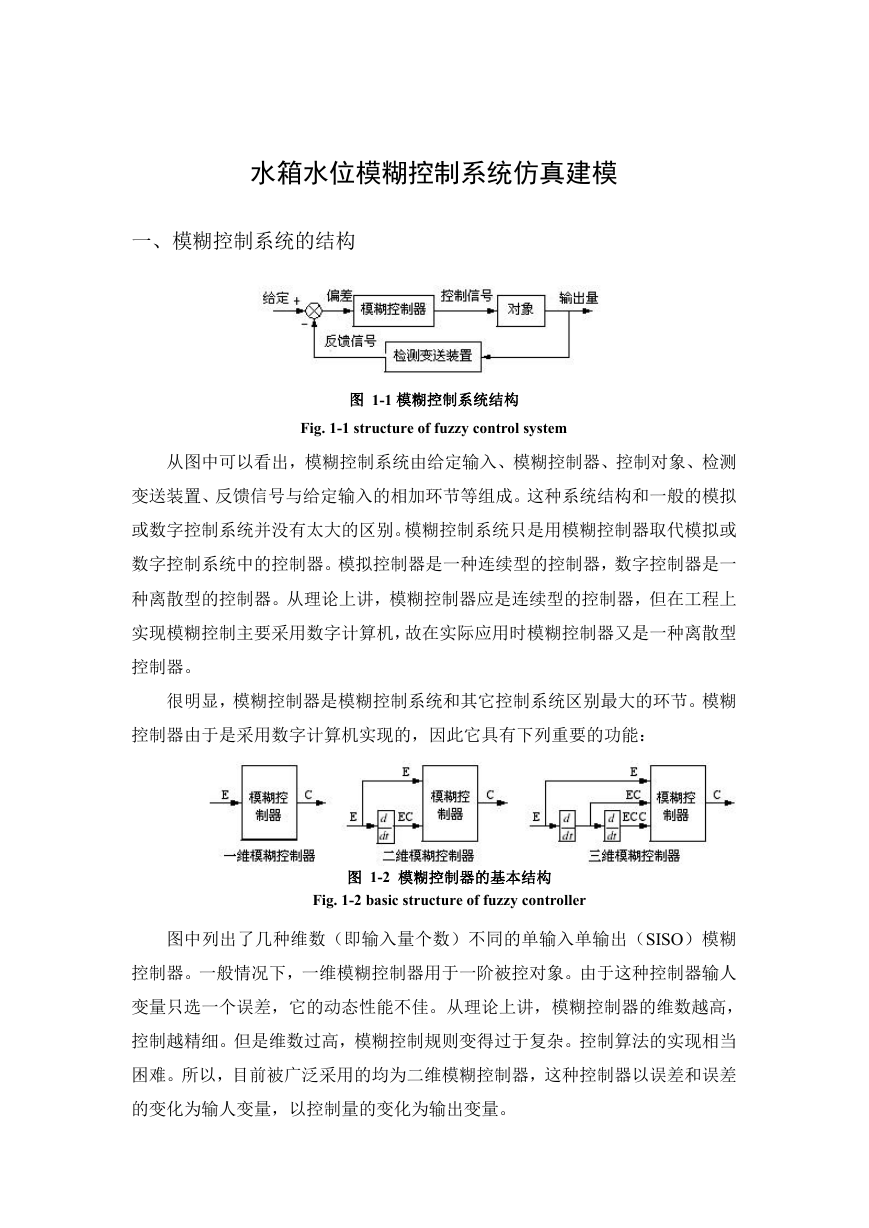
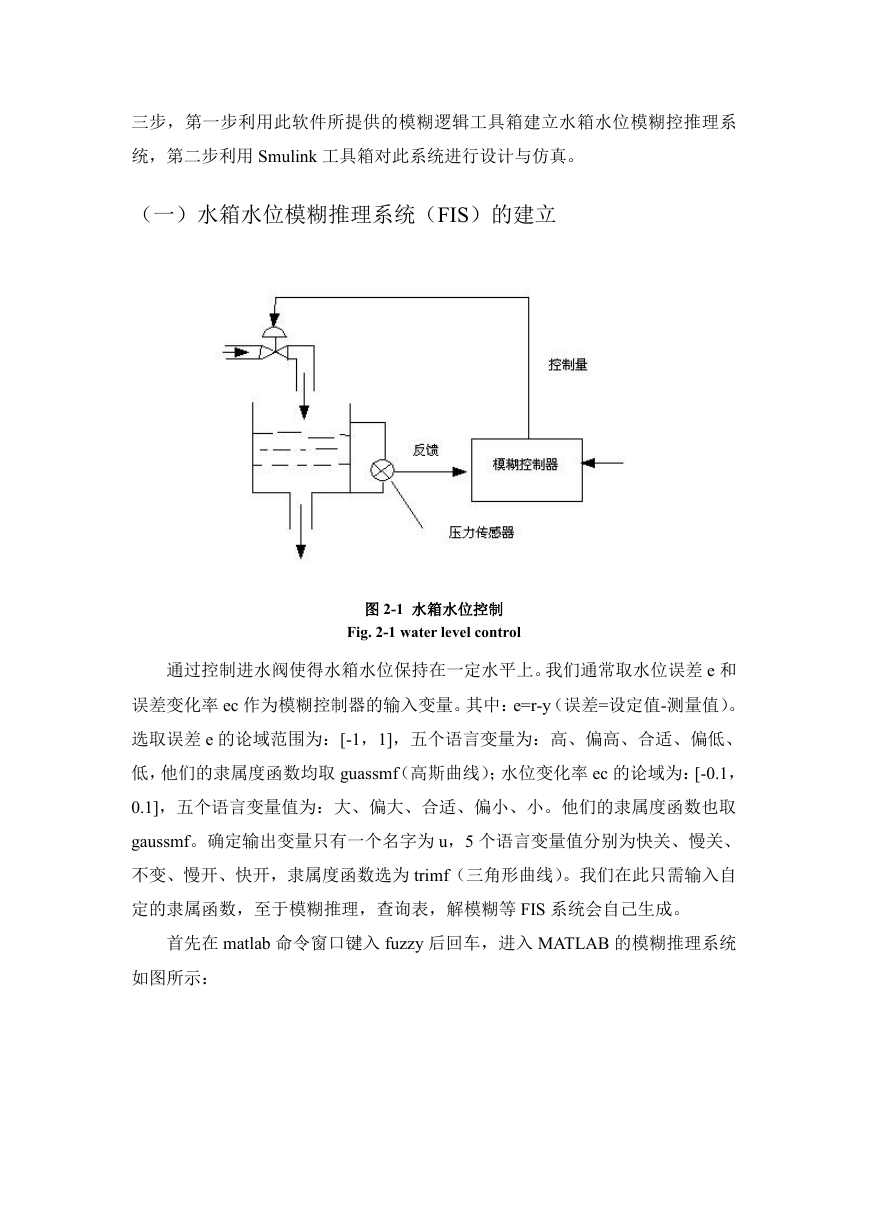
    水箱水位模糊控制系统仿真建模 一、模糊控制系统的结构 图 1-1 模糊控制系统结构 Fig. 1-1 structure of fuzzy control system 从图中可以看出，模糊控制系统由给定输入、模糊控制器、控制对象、检测 变送装置、反馈信号与给定输入的相加环节等组成。这种系统结构和一般的模拟 或数字控制系统并没有太大的区别。模糊控制系统只是用模糊控制器取代模拟或 数字控制系统中的控制器。模拟控制器是一种连续型的控制器，数字控制器是一 种离散型的控制器。从理论上讲，模糊控制器应是连续型的控制器，但在工程上 实现模糊控制主要采用数字计算机，故在实际应用时模糊控制器又是一种离散型 控制器。 很明显，模糊控制器是模糊控制系统和其它控制系统区别最大的环节。模糊 控制器由于是采用数字计算机实现的，因此它具有下列重要的功能： 图 1-2 模糊控制器的基本结构 Fig. 1-2 basic structure of fuzzy controller 图中列出了几种维数（即输入量个数）不同的单输入单输出（SISO）模糊 控制器。一般情况下，一维模糊控制器用于一阶被控对象。由于这种控制器输人 变量只选一个误差，它的动态性能不佳。从理论上讲，模糊控制器的维数越高， 控制越精细。但是维数过高，模糊控制规则变得过于复杂。控制算法的实现相当 困难。所以，目前被广泛采用的均为二维模糊控制器，这种控制器以误差和误差 的变化为输人变量，以控制量的变化为输出变量。
    利用模糊数学工具及模糊控制理论知识，建立一个水箱水位模糊控制器，水 位模糊控制器可以设计为二维控制器，即输入量是水位误差和误差变化率，输出 量是阀门控制量，但由于过程计算量大，计算复杂所以此章仅采用一维系统，即 单输入-单输出统，较复杂的二维系统将在下一章里利用 MUTLAB 软件构建，并 仿真。下图为水位模糊控制系统的基本结构。 压力传感器 设定 模糊控制器 M 反馈 控制量 图 1-3 水位模糊控制系统 Fig. 1-3 water level fuzzy control system 二、利用 MATLAB 对水箱水位系统进行仿真建模 用 MALAB 软件来对水箱水位模糊控制系统进行仿真建模试验，基本分为
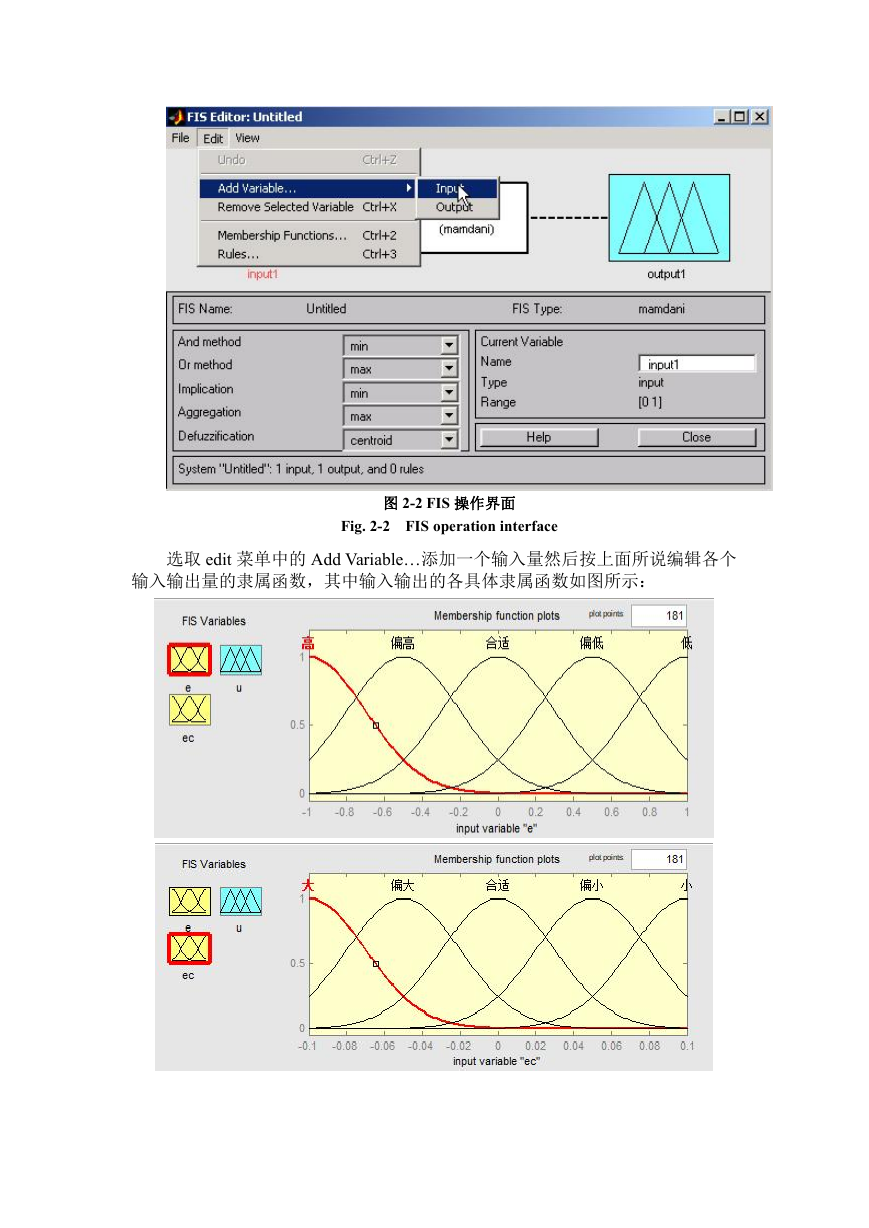
    三步，第一步利用此软件所提供的模糊逻辑工具箱建立水箱水位模糊控推理系 统，第二步利用 Smulink 工具箱对此系统进行设计与仿真。 （一）水箱水位模糊推理系统（FIS）的建立 图 2-1 水箱水位控制 Fig. 2-1 water level control 通过控制进水阀使得水箱水位保持在一定水平上。我们通常取水位误差 e 和 误差变化率 ec 作为模糊控制器的输入变量。其中：e=r-y（误差=设定值-测量值）。 选取误差 e 的论域范围为：[-1，1]，五个语言变量为：高、偏高、合适、偏低、 低，他们的隶属度函数均取 guassmf（高斯曲线）；水位变化率 ec 的论域为：[-0.1， 0.1]，五个语言变量值为：大、偏大、合适、偏小、小。他们的隶属度函数也取 gaussmf。确定输出变量只有一个名字为 u，5 个语言变量值分别为快关、慢关、 不变、慢开、快开，隶属度函数选为 trimf（三角形曲线）。我们在此只需输入自 定的隶属函数，至于模糊推理，查询表，解模糊等 FIS 系统会自己生成。 首先在 matlab 命令窗口键入 fuzzy 后回车，进入 MATLAB 的模糊推理系统 如图所示：
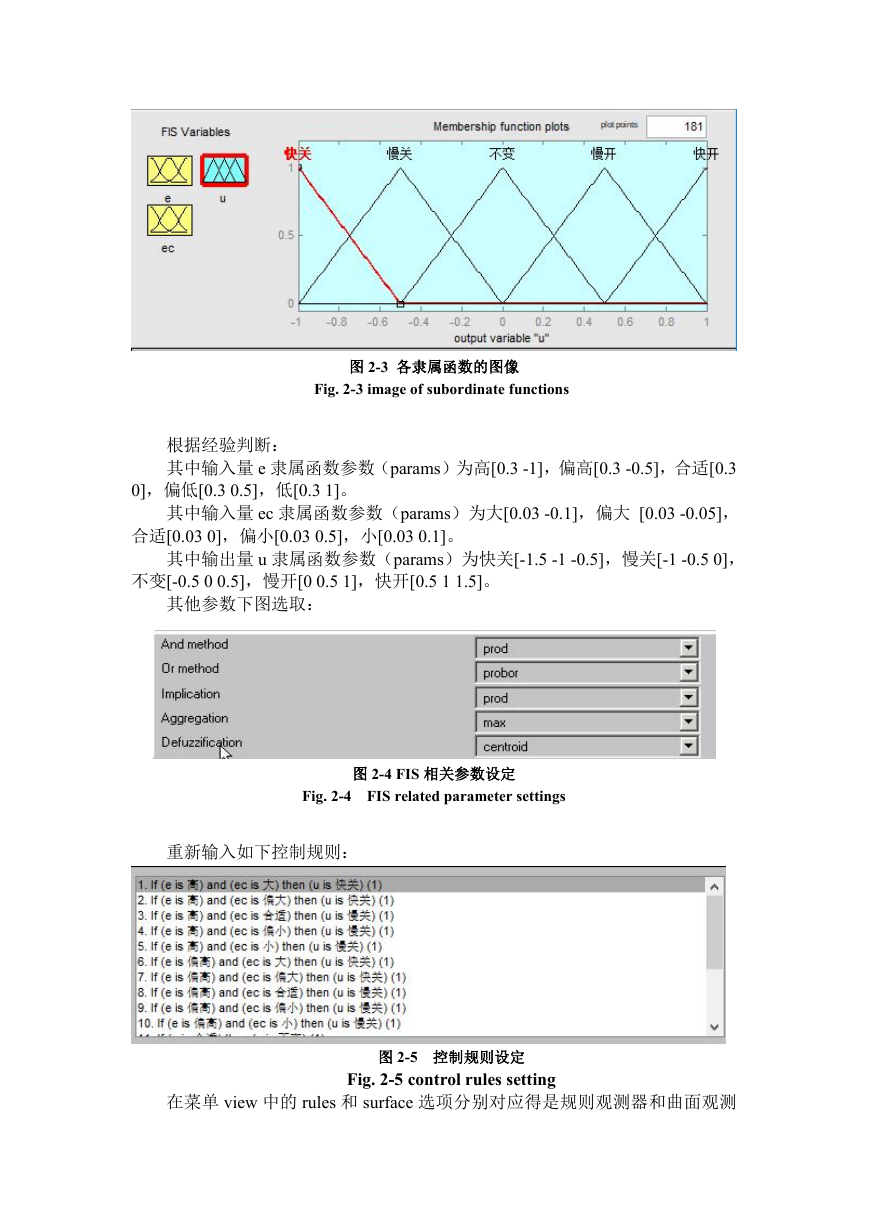
    图 2-2 FIS 操作界面 Fig. 2-2 FIS operation interface 选取 edit 菜单中的 Add Variable…添加一个输入量然后按上面所说编辑各个 输入输出量的隶属函数，其中输入输出的各具体隶属函数如图所示：
    图 2-3 各隶属函数的图像 Fig. 2-3 image of subordinate functions 根据经验判断： 其中输入量 e 隶属函数参数（params）为高[0.3 -1]，偏高[0.3 -0.5]，合适[0.3 0]，偏低[0.3 0.5]，低[0.3 1]。 其中输入量 ec 隶属函数参数（params）为大[0.03 -0.1]，偏大 [0.03 -0.05]， 合适[0.03 0]，偏小[0.03 0.5]，小[0.03 0.1]。 其中输出量 u 隶属函数参数（params）为快关[-1.5 -1 -0.5]，慢关[-1 -0.5 0]， 不变[-0.5 0 0.5]，慢开[0 0.5 1]，快开[0.5 1 1.5]。 其他参数下图选取： 图 2-4 FIS 相关参数设定 Fig. 2-4 FIS related parameter settings 重新输入如下控制规则： 在菜单 view 中的 rules 和 surface 选项分别对应得是规则观测器和曲面观测 Fig. 2-5 control rules setting 图 2-5 控制规则设定
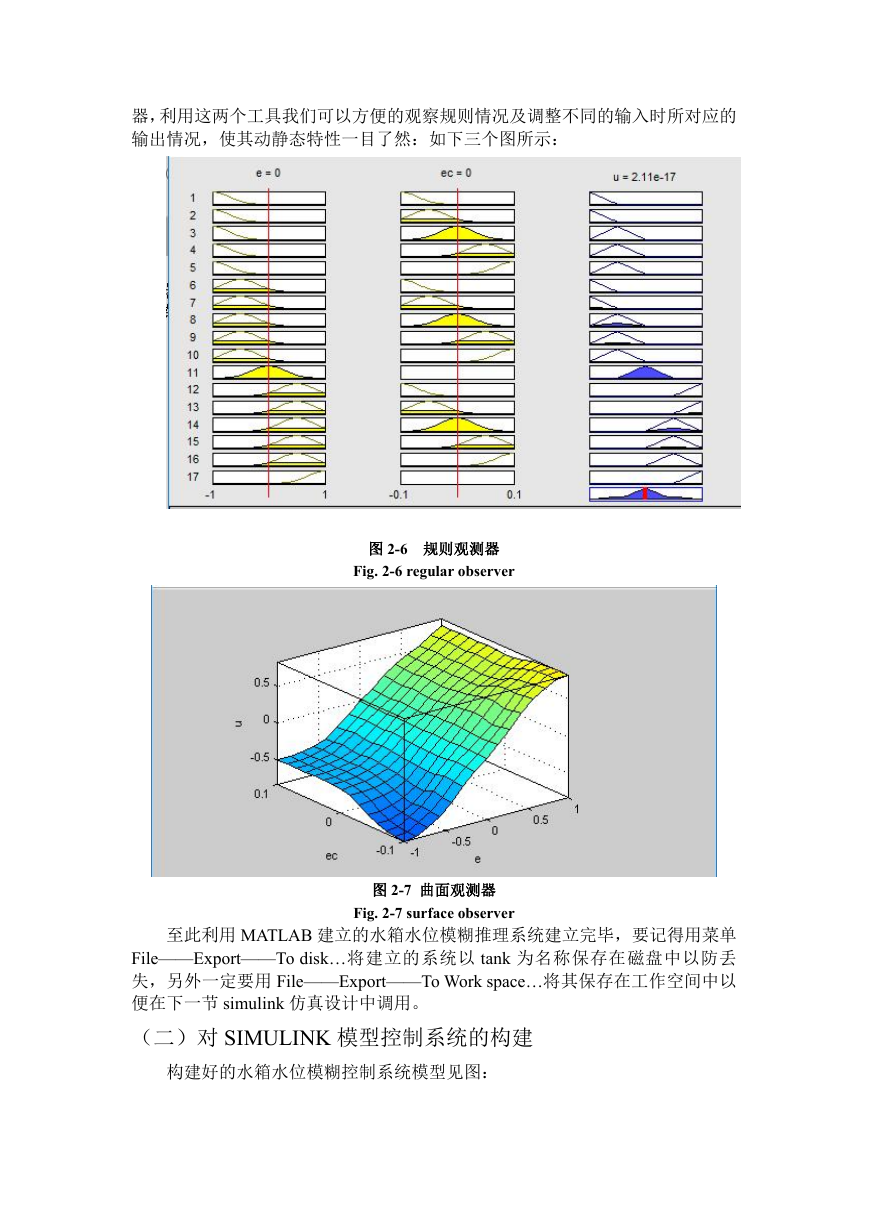
    器，利用这两个工具我们可以方便的观察规则情况及调整不同的输入时所对应的 输出情况，使其动静态特性一目了然：如下三个图所示： 图 2-6 规则观测器 Fig. 2-6 regular observer 图 2-7 曲面观测器 Fig. 2-7 surface observer 至此利用 MATLAB 建立的水箱水位模糊推理系统建立完毕，要记得用菜单 File——Export——To disk…将建立的系统以 tank 为名称保存在磁盘中以防丢 失，另外一定要用 File——Export——To Work space…将其保存在工作空间中以 便在下一节 simulink 仿真设计中调用。 （二）对 SIMULINK 模型控制系统的构建 构建好的水箱水位模糊控制系统模型见图：
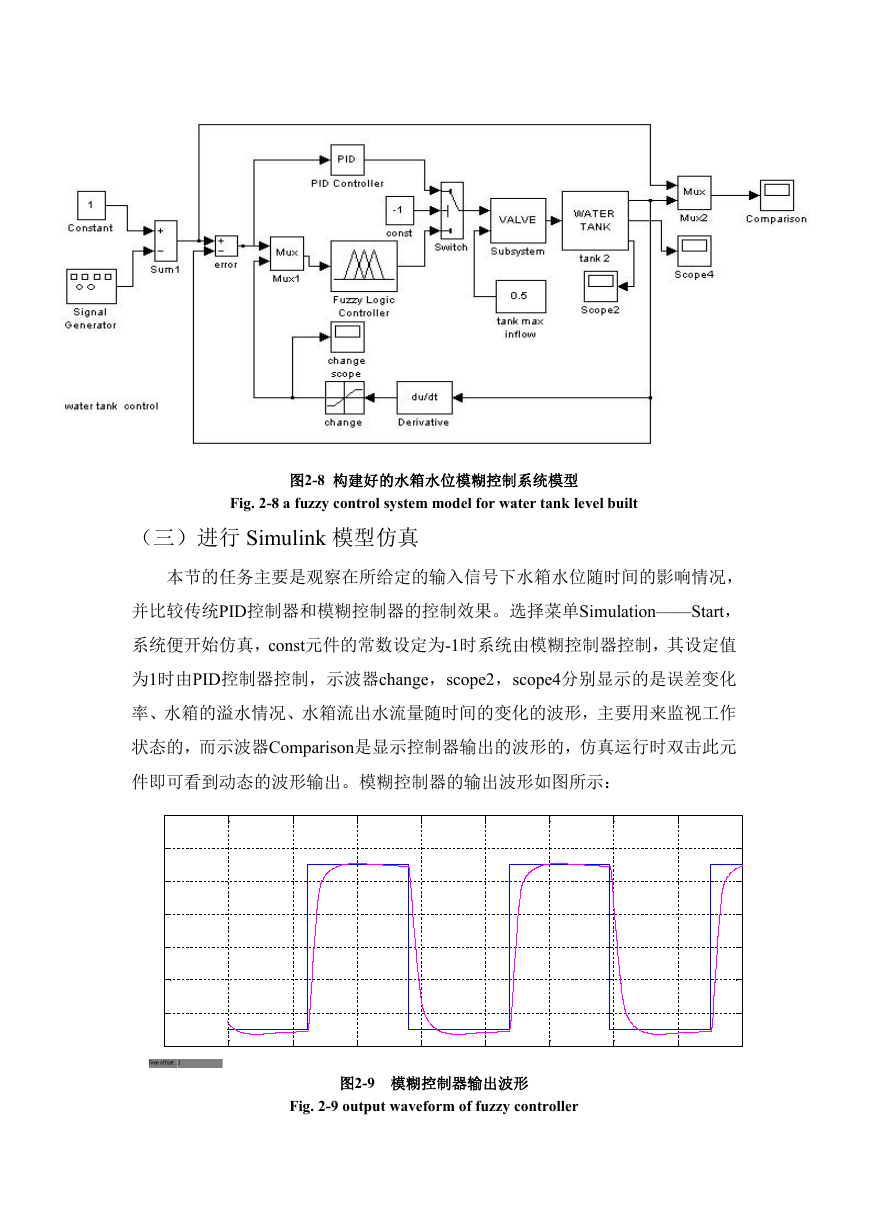
    图2-8 构建好的水箱水位模糊控制系统模型 Fig. 2-8 a fuzzy control system model for water tank level built （三）进行 Simulink 模型仿真 本节的任务主要是观察在所给定的输入信号下水箱水位随时间的影响情况， 并比较传统PID控制器和模糊控制器的控制效果。选择菜单Simulation——Start， 系统便开始仿真，const元件的常数设定为-1时系统由模糊控制器控制，其设定值 为1时由PID控制器控制，示波器change，scope2，scope4分别显示的是误差变化 率、水箱的溢水情况、水箱流出水流量随时间的变化的波形，主要用来监视工作 状态的，而示波器Comparison是显示控制器输出的波形的，仿真运行时双击此元 件即可看到动态的波形输出。模糊控制器的输出波形如图所示： 图2-9 模糊控制器输出波形 Fig. 2-9 output waveform of fuzzy controller
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料