logo资料库

压缩感知理论与傅立叶变换的地震数据重建.pdf

发布时间：2022-06-12 发布人：admin 分类：说明书 资料大小：1.49M 资料格式：pdf 举报 版权申诉
第1页 / 共11页
第2页 / 共11页
第3页 / 共11页
第4页 / 共11页
第5页 / 共11页
第6页 / 共11页
第7页 / 共11页
第8页 / 共11页
资料共11页，剩余部分请下载后查看
    2013 年 6 月 APPLIED GEOPHYSICS（应用地球物理） 第 10 卷，第 2 期 基于压缩感知理论与傅立叶变换的地震数据重建方法//Seismic data reconstruction based on CS and Fourier theory, APPLIED GEOPHYSICS, 2013, 10(2), P. 170-180. DOI: 10.1007/s11770-013-0375-3 基于压缩感知理论与傅立叶变换的地震数据 重建 张华 1,2，陈小宏 2，吴信民 1 （1. 东华理工大学放射性地质与勘探技术国防重点学科实验室，江西抚州 344000；2. 中国石油大学（北京）海洋石油勘探国家工程实验室，北京 102249） 摘要：传统的地震勘探数据采样必须遵循奈奎斯特采样定理，而本文基于新发展 的压缩感知理论，在突破传统采样定理限制的基础上，利用随机欠采样方法将传 统规则欠采样所带来的互相干假频转化成较低幅度的不相干噪声，从而将数据重 建问题转为更简单的去噪问题。在数据重建过程中引入凸集投影算法（POCS）， 采用指数规律衰减的阈值参数，在每次迭代过程中，改变以往从时间到空间都需 要进行正反变换的做法，提出只对地震数据空间方向进行正反变换，从而可以减 少内存空间，提高运算速度，并且也分析了本文POCS算法的抗噪声与反假频能力， 同时我们也对二维和三维地震数据重建进行了比较。理论模型和实际数据表明本 文方法效果明显，这对于指导复杂地区数据采集、缺失地震道重建及降低勘探成 本方面具有重要的实用价值。 关键字：傅立叶变换，压缩感知，凸集投影，数据重建 引言 在地震勘探中，地震数据体的采样已达到 了五维，数据采集面临着巨大的压力，为了恢 复高维的数据结构，我们不仅面临奈奎斯特采 样定理的限制，而且也面临由于地震数据采集 维数的增加而使得数据量呈指数增加的压力， 这两个方面目前成了地震勘探方法进一步应用 于 石 油 和 天 然 气 勘 探 领 域 中 的 最 大 的 挑 战 (Herrmann, 2010; Trad, 2009; Ma et al., 2010)。同 时，由于地形条件的限制和经济成本的考虑， 地震勘探数据沿空间方向上通常进行不规则采 样，这种稀疏分布的地震数据难以满足后续处 理的需求(Gao et al., 2011; 2008; Tang et al., 2010)。而压缩感知为解决此类问题提供了新的 契机(Donoho, 2006; Candès et al., 2006)，它可克 服传统奈奎斯特采样定理的不足，利用信号的 稀疏性，以远低于奈奎斯特采样率的速率对信 号进行非自适应的测量，从而可以压缩数据采 集量，降低勘探成本，而将成本转移到数据重 建的计算过程中来，其方法的核心是利用随机  收稿日期：2012-02-15；修改稿收到日期：2013-01-30 基金项目：本项研究由国家自然科学基金（编号：41174107）和国家科技油气重大专项（编号：2011ZX05023-005） 联合资助。 通讯作者：陈小宏 (E-mail: chenxh@cup.edu.cn) © 2013 应用地球物理编辑部，保留所有版权
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 欠采样方法将传统规则欠采样所带来的互相干 运算速度，更好地满足工业生产需求。 假频转化成较低幅度的不相干噪声，从而将数 据重建问题转为更简单的去噪问题。 在压缩感知理论框架下，对于不规则地震 数据的重建，广泛使用的方法是基于某种变换， 如Radon变换(Trad, 2003; Wang et al., 2010)，傅 里叶变换(Trad, 2009; Liu, 2004; Xu et al., 2005; Kreimer, 2012; Jin, 2010) ， Curvelet 变 换 (Herrmann, 2010; Hennenfent, 2008, 2010; Tang, 2010; Naghizadeh et al., 2010)等，该方法不需要 地下结构的先验信息，能够处理规则缺失和不 规则缺失地震道的重建，且计算速度快，精度 高，目前已经发展到了五维地震数据的重建 (Trad, 2009; Kreimer, 2012; Jin, 2010)，通过利用 多维地震数据信息，使得重建效果进一步提高， 所采用重建方法主要有最小加权范数方法(Liu, 2004; Trad, 2009;)、抗频谱泄露方法(Xu et al., 2005)、凸集投影算法(Abma, 2006; Galloway et al., 2007; Gao et al., 2010)以及多维匹配追踪算 法(Vassallo et al., 2010)。而对于凸集投影算法 （POCS），该方法最早由Bregman(1965)提出， 而后广泛应用于图像处理(Ozkan et al., 1994)， Abma(2006)将POCS算法应用于不规则地震数 据的重建，取得了较好的应用效果，在他的文 章中，POCS算法每次迭代都需要对时间和空间 上进行一次全局正反傅立叶变换，以下简称为 常规POCS算法，而后Gao(2010)对其进行简化， 在迭代前后只对时间方向进行一次正反傅立叶 变换，节省近50%时间，然而当数据重建到达 五维时，每次迭代过程中仍然需要进行五维数 组正反变换的运算，对计算机的内存要求较高， 且运算时间较长，显然满足不了处理海量地震 数据的要求。为此，本文在每次迭代运算过程 中，只对空间方向进行正反傅立叶变换，也即 为对时间切片进行数据重建，这样可以减少一 维正反傅立叶变换，使得在运算过程中降低数 据重建的维数，节省内存空间，尽管需要循环 对每个时间切片进行处理，但也可以提高部分 171 压缩感知理论 理论基础 压缩感知理论表明，即使在不满足奈奎斯 特采样定理要求的情况下，也有可能实现对原 始完整信号较好地逼近，但从严重的欠采样数 据中恢复出完整的数据所要满足三个条件：（1） 信号是稀疏的或者可压缩的；（2）测量矩阵是 随机的；（3）通过一定的重建策略来促进稀疏 化，完成上述问题的求解 。但地震勘探中，大 部分信号本身并不稀疏，通常都寻找到某种变 换来稀疏表示地震数据，本文使用傅立叶变换 作为稀疏基，然后通过一定的重建策略来促进 稀疏化。地震数据的重建问题可以描述为由一 组不完整数据通过线性算子的作用恢复出完整 的数据，假设如下线性正演模型 y = Mf （1） 0 nRy 代表采集的地震数据； NR0f 这里 ， n ， 表 示 待 重 建 的 无 假 频 数 据 ； 且 N 表示随机采样矩阵，假设数据 0x 是 0f n NR M 在变换域 C 中的稀疏表示，则方程（1）可以写 成： y Ax 且  0 def A MC （2） H 这里上标 H 代表共轭转置矩阵， A 为压缩感知 矩阵，当从采集的数据 y 中重建无假频数据 0f 时，由于 0x 是稀疏的，使得该欠定方程有解。 决 在稀疏促进反演后，重建信号由  Hf C x 定，同时：  x  arg min y Ax （3） 在这个表达式中， x 代表了估计值，L1范数定 subject to  x 1 def 义为 1  x N i 1  x ， [ ]ix 是向量 x 中第 i 个元 i [ ] 素，通过以上方程的求解，可以重建出无假频
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 地震数据（Hennenfent and Herrmann, 2008）。 速度，提高了计算效率，其公式为： 重建算法 i Max e    i ( 1)[ln(  ) ln(   N 1  Max )] （6） 1 1 H : :      从以上分析可知，压缩感知方法的关键技术 之一，是通过最小化策略求解上述欠定问题， 为此引入凸集投影算法，假设稀疏变换系数 x 是式（3）的解，则 1l 球  A p p x 和超  平面   p y MC p B 0  相交于一点，即：  A B x ，因此可以通过迭代的方法先投影到 集合 A ，然后投影到集合 B ，交替投影最终收 敛到 A B 中的一点。 POCS方法步骤为： i i （1）选择阈值参数 (   N 为迭代次数 ) ，初始化 0 y 样得到的地震数据。 1,2,3,  其中 y ，即输入随机采 N , , （ 2 ） 将 地 震 数 据 1iy 做 稀 疏 变 换 x Cy ，用 i作为阈值去除小于 i的值，  i 1  x T Cx ，下标 i 表示第 i 次迭代； iT 表 即 i 1  示阈值算子。 1  i  i i （3）将 ix 做反稀疏变换 y C x （4） i H i 式中 Max 为 Cy 的最大值，即稀疏变换系数绝 对值的最大值。 采样方式对比 一维采样方式 压缩感知的关键技术之一是随机欠采样方 法，因为它可以把混淆真实频率的相干噪声转 化成容易滤除的不相干噪声．即使这些随机噪 声和真实频谱相互叠合在一起，可以通过迭代 的方式检测出真实频率，因此，相干噪声的程 度，很自然地就成为衡量一种欠采样方法效果 的重要标准之一。 图1a为三个余弦函数的叠加信号，满足奈 奎斯特采样定理进行规则采样，且这个信号在 傅立叶域是稀疏的，图1b为其振幅谱。图1c为 50%随机欠采样，图1d为其振幅谱，从中可以 看出，假频转为不相干的随机噪声，这种情况 然后将不完整地震数据 y 的未缺失地震数 下，在噪声水平之上的重要信号系数能够被恢 复，这些系数能够通过促进稀疏的去噪技术进 行检测，从而精确地恢复出原始信号。这个例 子说明如果信号在傅立叶域是稀疏的，可以从 较为严重的欠采样中得到良好的恢复。图1e为 50%规则欠采样，规则欠采样所引起的假频与 真实频谱相似（图1f），这种情况下，由于在 傅立叶域待恢复的信号成分与假频都是稀疏 的，且峰值近似相等，稀疏促进恢复策略可能 失效。因此这个例子表明对于傅立叶域促进稀 疏的重建算法，随机欠采样比规则欠采样更加 有利。 据填充到 iy 上，即 I M y My （5）    y ( ) i i 然后将得到的 iy 代入步骤（２），重新进 行迭代，直到运行 N 次结束，再对迭代 N 次后 的 nx 做逆变换即可以得到最终的重建结果。 从上分析可知，POCS算法重点在于阈值 i 的选取，不同 i的选取方法直接影响到迭代求 解的收敛速度和精度，具体的参数选取可以参 考文献(Gao et al, 2010)，本文主要选取按照指数 规律衰减的阈值参数，这样可以加快了迭代的 172
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 图1 一维(欠)采样方式及其频谱分析 (a)规则采样信号；(c)随机欠采样；(e)规则欠采样；(b)(d)(f)为对应频谱 二维采样方式 由于一维采样方式只沿着一个空间轴的方 向采集地震道，重建效果有限，同时也不满足 野外数据采集的要求，因此需要发展二维的采 样方式，沿着两个空间轴的方向进行数据采集， 图2a为合成地震叠前数据的某一时间切片模 型，满足奈奎斯特采样定理进行规则采样，横 坐标表示检波器，纵坐标表示炮点，图2b为其 二维频谱分析，可看出该数据在傅立叶域是稀 疏的，满足压缩感知理论要求，图2c为50%随机 欠采样，图2d为其二维频谱分析，从中可以看 出，由于采样矩阵是随机的，和信号本身不相 干，因此引起的假频转为不相干的随机噪声， 真实频谱可以通过阈值算法进行检测，从而将 数据重建问题转为更为简单的去噪问题，在满 足一定精度要求下恢复出原始数据。图1e为50% 规则欠采样，规则欠采样所引起的假频与真实 频谱较为接近（图2f），稀疏促进恢复策略可 能会受到一定的影响。 173
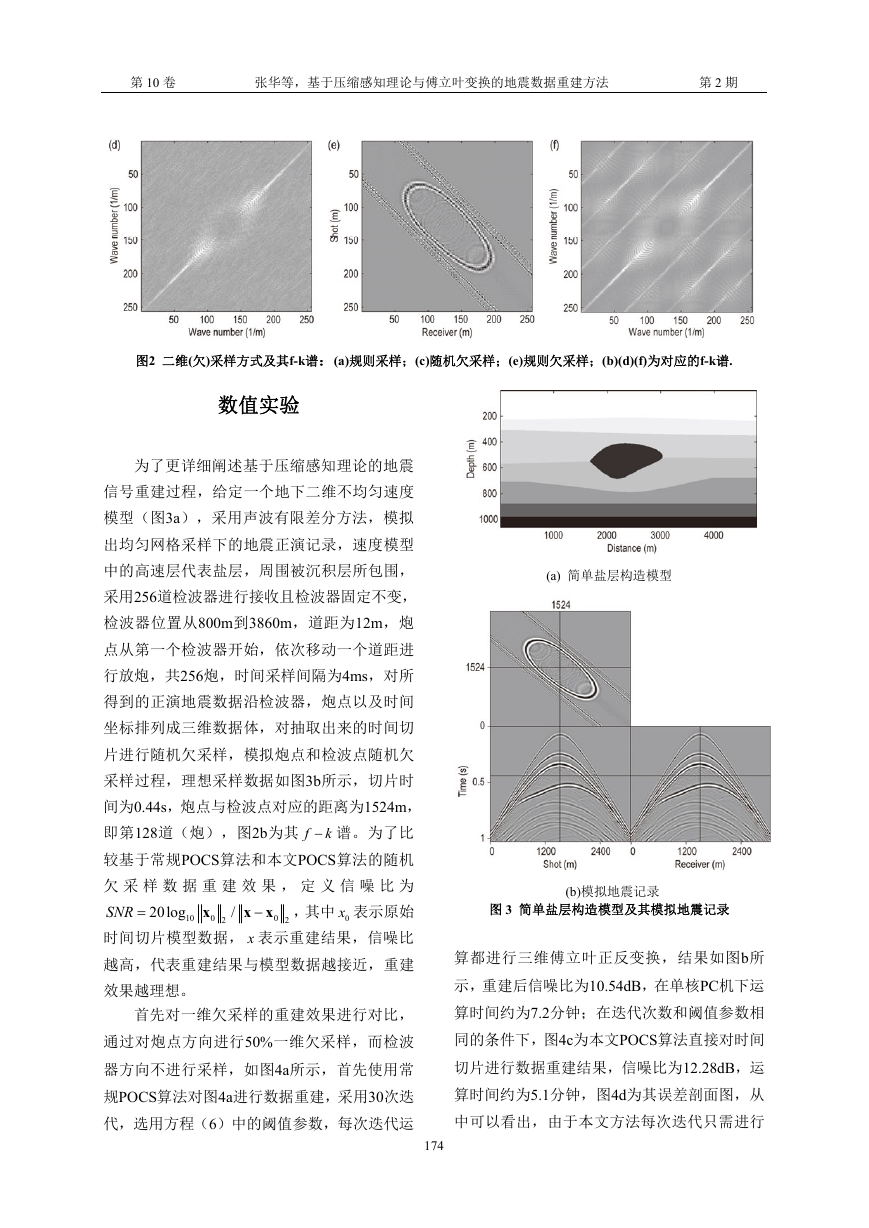
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 图2 二维(欠)采样方式及其f-k谱：(a)规则采样；(c)随机欠采样；(e)规则欠采样；(b)(d)(f)为对应的f-k谱. 数值实验 为了更详细阐述基于压缩感知理论的地震 信号重建过程，给定一个地下二维不均匀速度 模型（图3a），采用声波有限差分方法，模拟 出均匀网格采样下的地震正演记录，速度模型 中的高速层代表盐层，周围被沉积层所包围， 采用256道检波器进行接收且检波器固定不变， 检波器位置从800m到3860m，道距为12m，炮 点从第一个检波器开始，依次移动一个道距进 行放炮，共256炮，时间采样间隔为4ms，对所 得到的正演地震数据沿检波器，炮点以及时间 坐标排列成三维数据体，对抽取出来的时间切 (a) 简单盐层构造模型 片进行随机欠采样，模拟炮点和检波点随机欠 采样过程，理想采样数据如图3b所示，切片时 间为0.44s，炮点与检波点对应的距离为1524m， 即第128道（炮），图2b为其 f k 谱。为了比 较基于常规POCS算法和本文POCS算法的随机 欠 采 样 数 据 重 建 效 果 ， 定 义 信 噪 比 为 x x ，其中 0x 表示原始 SNR   时间切片模型数据， x 表示重建结果，信噪比 20log 10 / x 0 2 0 2 越高，代表重建结果与模型数据越接近，重建 效果越理想。 首先对一维欠采样的重建效果进行对比， 通过对炮点方向进行50%一维欠采样，而检波 器方向不进行采样，如图4a所示，首先使用常 规POCS算法对图4a进行数据重建，采用30次迭 代，选用方程（6）中的阈值参数，每次迭代运 174 (b)模拟地震记录 图 3 简单盐层构造模型及其模拟地震记录 算都进行三维傅立叶正反变换，结果如图b所 示，重建后信噪比为10.54dB，在单核PC机下运 算时间约为7.2分钟；在迭代次数和阈值参数相 同的条件下，图4c为本文POCS算法直接对时间 切片进行数据重建结果，信噪比为12.28dB，运 算时间约为5.1分钟，图4d为其误差剖面图，从 中可以看出，由于本文方法每次迭代只需进行
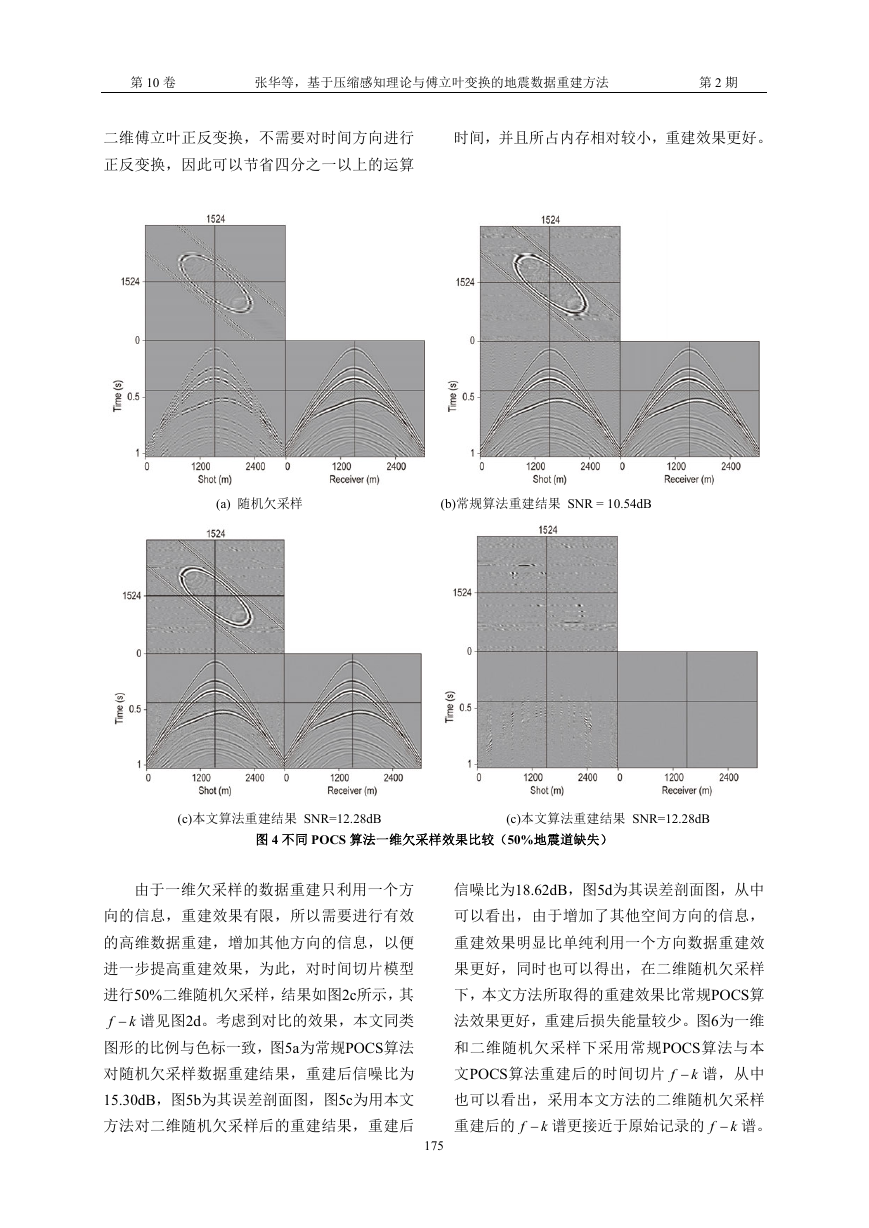
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 二维傅立叶正反变换，不需要对时间方向进行 正反变换，因此可以节省四分之一以上的运算 时间，并且所占内存相对较小，重建效果更好。 (a) 随机欠采样 (b)常规算法重建结果 SNR = 10.54dB (c)本文算法重建结果 SNR=12.28dB (c)本文算法重建结果 SNR=12.28dB 图 4 不同 POCS 算法一维欠采样效果比较（50%地震道缺失） 由于一维欠采样的数据重建只利用一个方 向的信息，重建效果有限，所以需要进行有效 信噪比为18.62dB，图5d为其误差剖面图，从中 可以看出，由于增加了其他空间方向的信息， 的高维数据重建，增加其他方向的信息，以便 重建效果明显比单纯利用一个方向数据重建效 进一步提高重建效果，为此，对时间切片模型 进行50%二维随机欠采样，结果如图2c所示，其 k 谱见图2d。考虑到对比的效果，本文同类 f 图形的比例与色标一致，图5a为常规POCS算法 对随机欠采样数据重建结果，重建后信噪比为 15.30dB，图5b为其误差剖面图，图5c为用本文 方法对二维随机欠采样后的重建结果，重建后 175 果更好，同时也可以得出，在二维随机欠采样 下，本文方法所取得的重建效果比常规POCS算 法效果更好，重建后损失能量较少。图6为一维 和二维随机欠采样下采用常规POCS算法与本 文POCS算法重建后的时间切片 f k 谱，从中 也可以看出，采用本文方法的二维随机欠采样 k 谱。 重建后的 f k 谱更接近于原始记录的 f
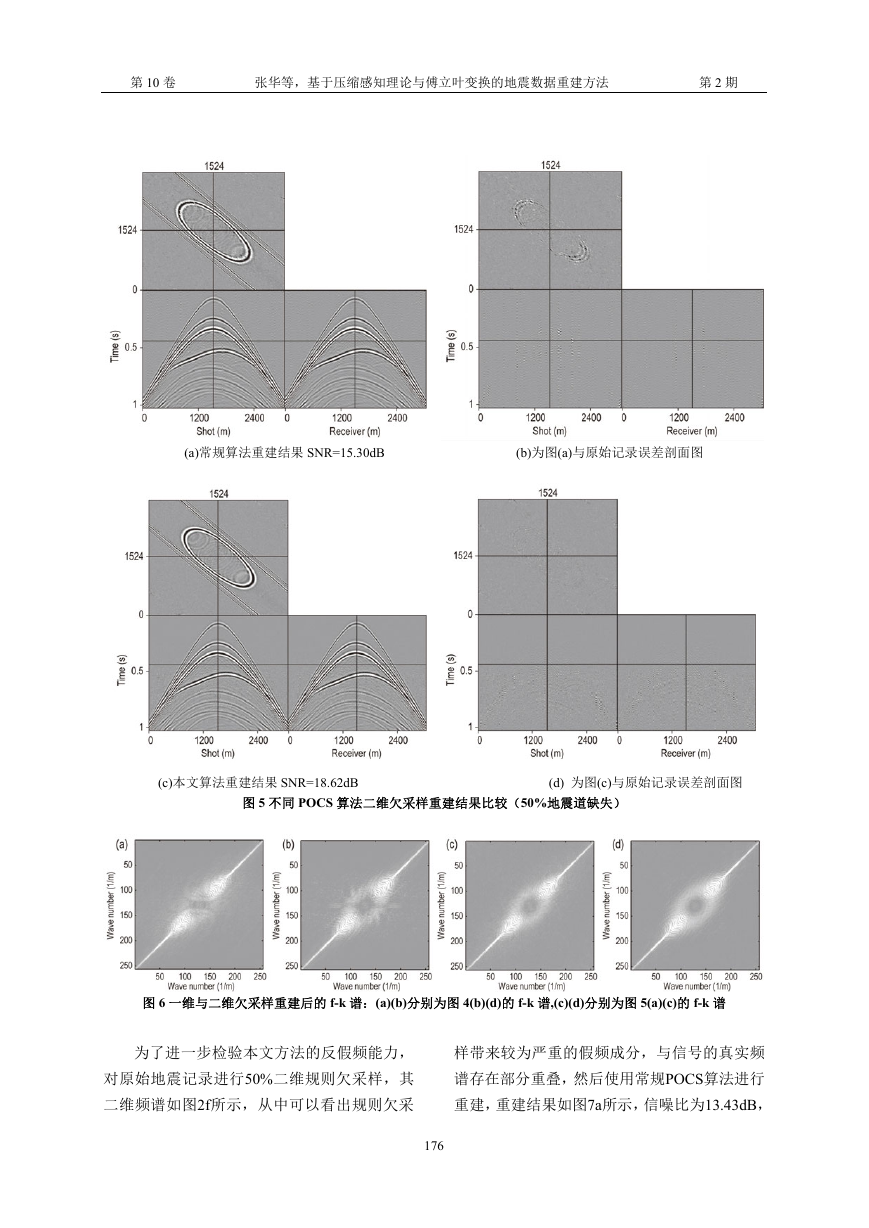
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 (a)常规算法重建结果 SNR=15.30dB (b)为图(a)与原始记录误差剖面图 (c)本文算法重建结果 SNR=18.62dB (d) 为图(c)与原始记录误差剖面图 图 5 不同 POCS 算法二维欠采样重建结果比较（50%地震道缺失） 图 6 一维与二维欠采样重建后的 f-k 谱：(a)(b)分别为图 4(b)(d)的 f-k 谱,(c)(d)分别为图 5(a)(c)的 f-k 谱 为了进一步检验本文方法的反假频能力， 对原始地震记录进行50%二维规则欠采样，其 二维频谱如图2f所示，从中可以看出规则欠采 样带来较为严重的假频成分，与信号的真实频 谱存在部分重叠，然后使用常规POCS算法进行 重建，重建结果如图7a所示，信噪比为13.43dB， 176
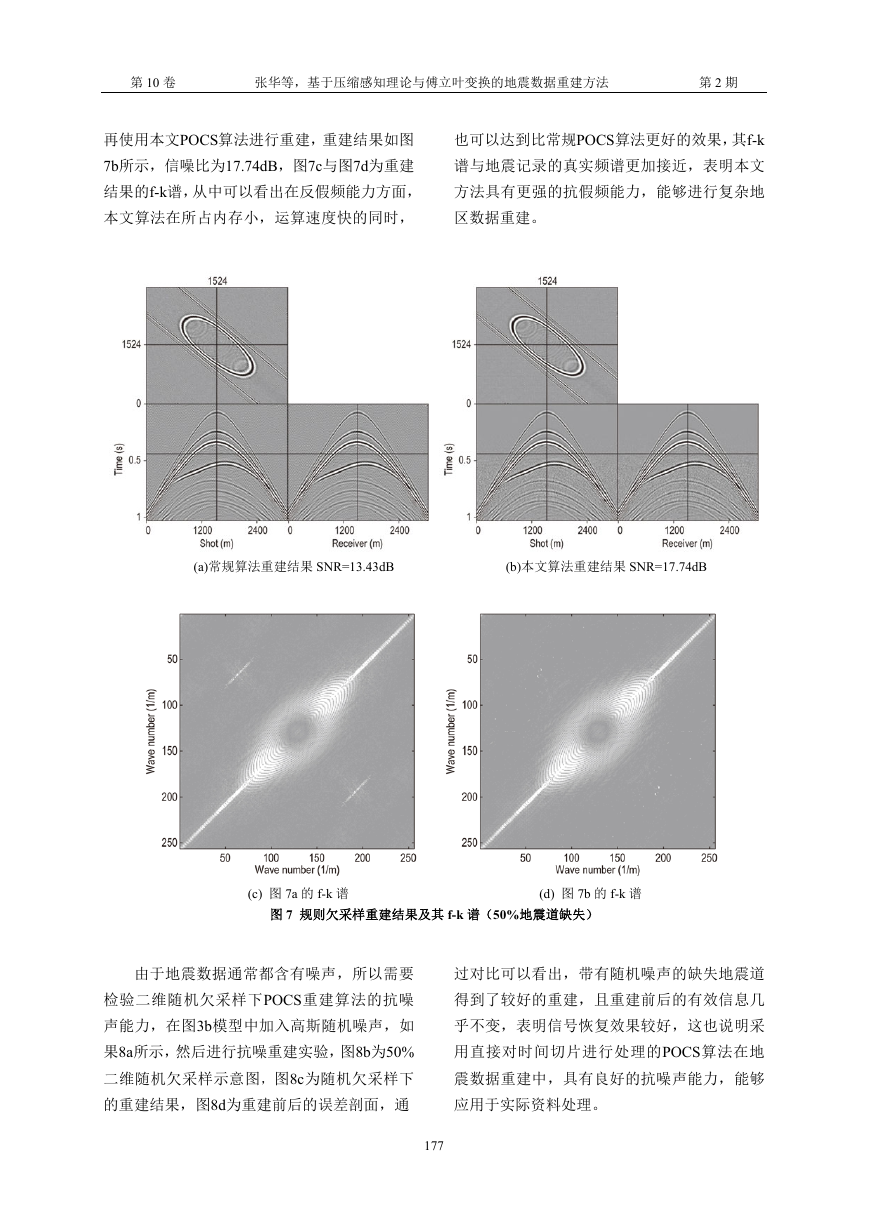
    第 10 卷 张华等，基于压缩感知理论与傅立叶变换的地震数据重建方法 第 2 期 再使用本文POCS算法进行重建，重建结果如图 7b所示，信噪比为17.74dB，图7c与图7d为重建 结果的f-k谱，从中可以看出在反假频能力方面， 本文算法在所占内存小，运算速度快的同时， 也可以达到比常规POCS算法更好的效果，其f-k 谱与地震记录的真实频谱更加接近，表明本文 方法具有更强的抗假频能力，能够进行复杂地 区数据重建。 (a)常规算法重建结果 SNR=13.43dB (b)本文算法重建结果 SNR=17.74dB (c) 图 7a 的 f-k 谱 (d) 图 7b 的 f-k 谱 图 7 规则欠采样重建结果及其 f-k 谱（50%地震道缺失） 由于地震数据通常都含有噪声，所以需要 检验二维随机欠采样下POCS重建算法的抗噪 声能力，在图3b模型中加入高斯随机噪声，如 果8a所示，然后进行抗噪重建实验，图8b为50% 二维随机欠采样示意图，图8c为随机欠采样下 的重建结果，图8d为重建前后的误差剖面，通 177 过对比可以看出，带有随机噪声的缺失地震道 得到了较好的重建，且重建前后的有效信息几 乎不变，表明信号恢复效果较好，这也说明采 用直接对时间切片进行处理的POCS算法在地 震数据重建中，具有良好的抗噪声能力，能够 应用于实际资料处理。
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料