第1页 / 共43页
第2页 / 共43页
第3页 / 共43页
第4页 / 共43页
第5页 / 共43页
第6页 / 共43页
第7页 / 共43页
第8页 / 共43页
深度生成模型综述（发表自自动化学报）.pdf
自动化学报
Acta Automatica Sinica
ISSN 0254-4156,CN 11-2109/TP
《自动化学报》网络首发论文
深度生成模型综述
题目：
胡铭菲，刘建伟，左信
作者：
10.16383/j.aas.c190866
DOI：
收稿日期：
2019-12-19
网络首发日期： 2020-09-21
引用格式：
胡铭菲，刘建伟，左信．深度生成模型综述．自动化学报.
https://doi.org/10.16383/j.aas.c190866
网络首发：在编辑部工作流程中，稿件从录用到出版要经历录用定稿、排版定稿、整期汇编定稿等阶
段。录用定稿指内容已经确定，且通过同行评议、主编终审同意刊用的稿件。排版定稿指录用定稿按照期
刊特定版式（包括网络呈现版式）排版后的稿件，可暂不确定出版年、卷、期和页码。整期汇编定稿指出
版年、卷、期、页码均已确定的印刷或数字出版的整期汇编稿件。录用定稿网络首发稿件内容必须符合《出
版管理条例》和《期刊出版管理规定》的有关规定；学术研究成果具有创新性、科学性和先进性，符合编
辑部对刊文的录用要求，不存在学术不端行为及其他侵权行为；稿件内容应基本符合国家有关书刊编辑、
出版的技术标准，正确使用和统一规范语言文字、符号、数字、外文字母、法定计量单位及地图标注等。
为确保录用定稿网络首发的严肃性，录用定稿一经发布，不得修改论文题目、作者、机构名称和学术内容，
只可基于编辑规范进行少量文字的修改。
出版确认：纸质期刊编辑部通过与《中国学术期刊（光盘版）》电子杂志社有限公司签约，在《中国
学术期刊（网络版）》出版传播平台上创办与纸质期刊内容一致的网络版，以单篇或整期出版形式，在印刷
出版之前刊发论文的录用定稿、排版定稿、整期汇编定稿。因为《中国学术期刊（网络版）》是国家新闻出
版广电总局批准的网络连续型出版物（ISSN 2096-4188，CN 11-6037/Z），所以签约期刊的网络版上网络首
发论文视为正式出版。
网络首发时间：2020-09-21 13:41:00
网络首发地址：https://kns.cnki.net/kcms/detail/11.2109.tp.20200921.1015.001.html
自 动 化 学 报
ACTA AUTOMATICA SINICA
深度生成模型综述
胡铭菲 1 刘建伟 1 左信 1
摘要 通过学习可观测数据的概率密度而随机生成样本的生成模型在近年来受到人们的广泛关注，网络结构中包含多个隐
藏层的深度生成式模型以更出色的生成能力成为研究热点，深度生成模型在计算机视觉、密度估计、自然语言和语音识别、
半监督学习等领域得到成功应用，并给无监督学习提供了良好的范式。本文根据深度生成模型处理似然函数的不同方法将
模型分为三类：第一类方法是近似方法，包括采用抽样方法近似计算似然函数的受限玻尔兹曼机和以受限玻尔兹曼机为基
础模块的深度置信网络、深度玻尔兹曼机和亥姆霍兹机，与之对应的另一种模型是直接优化似然函数变分下界的变分自编
码器以及其重要的改进模型，包括重要性加权自编码和可用于半监督学习的深度辅助深度模型；第二类方法是避开求极大
似然过程的隐式方法，其代表模型是通过生成器和判别器之间的对抗行为来优化模型参数从而巧妙避开求解似然函数的生
成对抗网络以及重要的改进模型，包括 WGAN、深度卷积生成对抗网络和当前最顶级的深度生成模型 BigGAN；第三类方
法是对似然函数进行适当变形的流模型和自回归模型，流模型利用可逆函数构造似然函数后直接优化模型参数，包括以
NICE 为基础的常规流模型、变分流模型和可逆残差网络（i-ResNet），自回归模型（NADE）将目标函数分解为条件概率
乘积的形式，包括神经自回归密度估计（NADE）、像素循环神经网络（PixelRNN）、掩码自编码器（MADE）以及 WaveNet
等。详细描述上述模型的原理和结构以及模型变形后，阐述各个模型的研究进展和应用，最后对深度生成式模型进行展望
和总结。
关键词 深度生成式模型, 受限玻尔兹曼机, 变分自编码器, 流模型, 生成对抗网络, 自回归分布估计
引用格式 胡铭菲，刘建伟，左信. 深度生成模型综述.自动化学报, 20XX,XX(X): X—X
DOI 10.16383/j.aas.c190866
Survey on Deep Generative Model
HU Ming-Fei1 LIU Jian-Wei1 ZUO Xin1
Abstract The generative model, which can generate samples randomly by learning the probability density of observable data, has
been widely concerned for the past few years. It has been successfully applied in a wide range of fields, such as image generation,
image restoration, density estimation, natural language and speech recognition, style transfer and super resolution, and so on. Deep
generative model with multiple hidden layers in the network structure becomes a research hotspot because of its better generation
ability. Depending on the different methods of calculating the maximum likelihood function, we divide the models into three types:
the first kind of method is the approximate method, which use the sampling method to calculate approximately the likelihood
function, such as Restricted Boltzmann machines and Deep Belief Network, Deep Boltzmann Machines, helmholtz machine based
on RBM. The alternatives are to optimize directly the variational lower bound of likelihood function, it is named as variational
autoencoder. The important improvements to these variants include Importance Weighted Autoencoders and Auxiliary Deep
Generative Models; the second kind is implicit methods, the representative model is Generative Adversarial Nets, GAN’s model
parameters is optimized by the adversaring behavior between the generator and the discriminator. The principal instantiations of
GAN include Wasserstein GAN, Deep Convolutional Generative Adversarial Networks and BigGAN. The third kind involve Flow
and Neural Autoregressive Net, the main variations of the Flow paradigm include Normalizing Flow based on Nonlinear
Independent Components Estimation, Invertible Residual Networks and Variational Inference with Flow. The successful
improvements to the Neural Autoregressive Net include Neural Autoregressive Distribution Estimation, Pixel Recurrent Neural
收稿日期 2019‐12‐19 录用日期 2020‐07‐27
Manuscript received December 19, 2019; accepted July 27, 2020
国家重点研发计划项目(2016YFC0303703)资助
Supported by National Key Research and Development Program of China (2016YFC0303703)
1. 中国石油大学（北京）自动化系 北京 102249
1. Department of Automation, China University of Petroleum, Beijing 102249
1
胡铭菲等： 深度生成模型综述
Network, Masked Autoencoder for Distribution Estimation and WaveNet. We outline the principle and structure of these deep
generative models, and look forward to the future work.
Key words deep generative models, restricted boltzmann machine, variational auto-encoder, flow, generative adversarial nets,
neural autoregressive distribution estimator
Citation Hu Ming-Fei,Liu Jian-Wei,Zuo Xin. Survey on deep generate model.Acta Automatica Sinica, 20XX, XX(X): X—X
受益于当前计算机性能的快速提升，学习可观
测样本的概率密度并随机生成新样本的生成模型
成为热点。相比于需要学习条件概率分布的判别模
型，生成模型的训练难度大、模型结构复杂，但除
了能够生成新样本外，生成模型在图像重构、缺失
数据填充、密度估计、风格迁移和半监督学习等应
用领域也获得了巨大的成功。当前可观测样本的数
量和维数都大幅度增加，浅层的生成模型受到性能
瓶颈的限制而无法满足应用需求，从而被含有多个
隐藏层的深度生成模型替代，深度生成模型能够学
习到更好的隐表示，模型性能更好。 本文对有重要
意义的深度生成模型进行全面的分析和讨论，对各
大类模型的结构和基本原理进行梳理和分类。本文
第 1 节介绍深度生成模型的概念和分类；第 2 节介
绍受限玻尔兹曼机和以受限玻尔兹曼机为基础模
块的几种深度生成模型，重点内容是各种模型的不
同训练算法；第 3 节介绍变分自编码器的基本结构、
变分下界的推理和重参数化方法；第 4 节介绍生成
对抗网络，主要内容为模型原理、训练方法和稳定
性研究，以及两种重要的模型结构；第 5 节总结了
流模型的结构，详细介绍了流模型的技术特点；第
6 节分析了自回归模型的模型结构以及几种重要分
支的研究进展；第 7 节将介绍生成模型中的两个小
分支：矩阵匹配模型和随机生成模型；第 8 节对深
度生成模型存在的问题进行分析讨论，并对未来的
研究方向和发展趋势做出了展望。
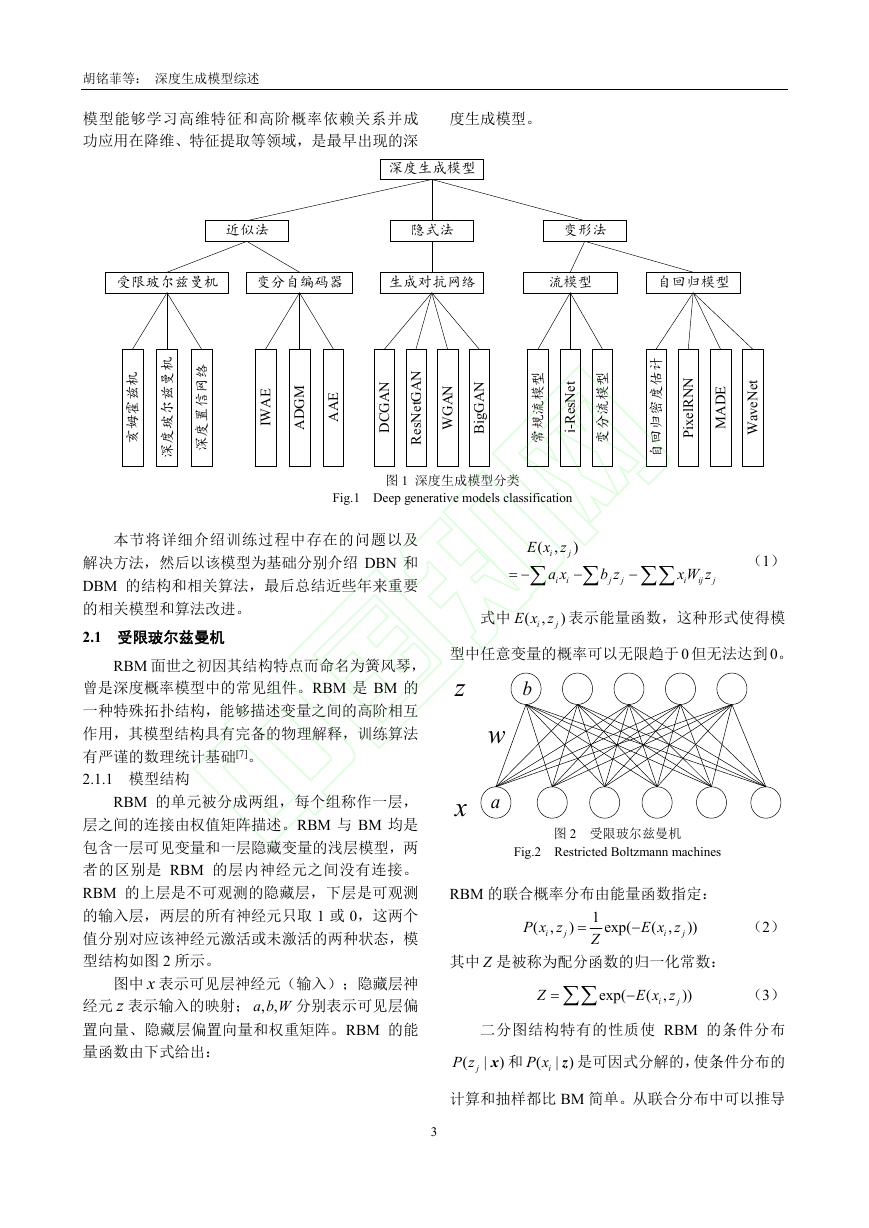
1 深度生成模型概述
深度生成模型的目标函数是数据分布与模型
分布之间的距离，可以用极大似然法进行求解。从
处理极大似然函数的方法的角度，可将深度生成模
型分成如下三种，分类内容如图 1 所示。具体分类
方式如下：
第一种方法是通过变分或抽样的方法求似然
函数的近似分布，这种方法可称为近似方法，主要
包括受限玻尔兹曼机[1]和变分自编码器[2]。用抽样
方法近似求解似然函数的受限玻尔兹曼机属于浅
层模型，以该模型为基础模块的深度生成模型包括
深度玻尔兹曼机和深度置信网络两种；变分自编码
2
器用似然函数的变分下界作为目标函数，这种使用
变分下界替代似然函数的近似方法的效率比受限
玻尔兹曼机的抽样方法高很多，实际效果也更好，
变分自编码器具有代表性的模型包括重要性加权
自编码、辅助深度生成模型等。
第二种方法是避开求极大似然过程的隐式方
法，其代表模型是生成对抗网络[3]。生成对抗网络
利用神经网络的学习能力来拟合两个分布之间的
距离，巧妙地避开了求解似然函数的难题，是目前
最成功、最有影响力的生成模型，其具有代表性的
模型很多，例如深度卷积生成对抗网络、WGAN 和
当前生成能力最好的 BigGAN；另外利用参数化马
尔科夫过程代替直接参数化似然函数的生成随机
网络[4]也属于此类方法。
第三类方法是对似然函数进行适当变形，变形
的目的是为了简化计算，此类方法包括流模型[5]和
自回归模型[6]两种模型。流模型利用可逆网络构造
似然函数之后直接优化模型参数，训练出的编码器
利用可逆结构的特点直接得到生成模型。流模型包
括常规流模型、变分流模型和可逆残差网络三种；
自回归模型将目标函数分解为条件概率乘积的形
式，这类模型有很多，具有代表性的包括像素循环
神经网络、掩码自编码器以及成功生成逼真的人类
语音样本的 WaveNet 等。
2 受限玻尔兹曼机
玻尔兹曼机（Boltzmann machines，BM）是由
能量函数定义的结构化无向图概率模型，用于学习
二值向量上的任意概率分布，广义上把基于能量的
模型都称作 BM。BM 层内各单元之间和各层之间
均为全连接关系，权值大小表示单元之间的相互作
用关系。BM 变种的流行程度早已超过了该模型
本身，其中最主要的衍生模型是属于生成模型的
受 限 玻 尔 兹 曼 机 RBM[1] （ Restricted Boltzmann
machines，RBM）和以 RBM 为基础模块的深度置
信网络（Deep Belief Network，DBN）和深度玻尔
兹曼机（Deep Boltzmann Machines，DBM）等深度
生成模型，是深度学习中的典型代表，曾受到广泛
研究，国内外均有关于该模型的综述文章[7-8]。这类
胡铭菲等： 深度生成模型综述
模型能够学习高维特征和高阶概率依赖关系并成
功应用在降维、特征提取等领域，是最早出现的深
度生成模型。
深度生成模型
近似法
隐式法
变形法
受限玻尔兹曼机
变分自编码器
生成对抗网络
流模型
自回归模型
机
兹
霍
姆
亥
机
曼
兹
尔
玻
度
深
络
网
信
置
度
深
E
A
W
I
M
G
D
A
E
A
A
N
A
G
C
D
N
A
G
t
e
N
s
e
R
N
A
G
W
N
A
G
g
i
B
型
模
流
规
常
t
e
N
s
e
R
-
i
型
模
流
分
变
图 1 深度生成模型分类
Fig.1 Deep generative models classification
计
估
度
密
归
回
自
N
N
R
l
e
x
i
P
E
D
A
M
t
e
N
e
v
a
W
本节将详细介绍训练过程中存在的问题以及
解决方法，然后以该模型为基础分别介绍 DBN 和
DBM 的结构和相关算法，最后总结近些年来重要
的相关模型和算法改进。
2.1 受限玻尔兹曼机
RBM 面世之初因其结构特点而命名为簧风琴，
曾是深度概率模型中的常见组件。RBM 是 BM 的
一种特殊拓扑结构，能够描述变量之间的高阶相互
作用，其模型结构具有完备的物理解释，训练算法
有严谨的数理统计基础[7]。
2.1.1 模型结构
RBM 的单元被分成两组，每个组称作一层，
层之间的连接由权值矩阵描述。RBM 与 BM 均是
包含一层可见变量和一层隐藏变量的浅层模型，两
者的区别是 RBM 的层内神经元之间没有连接。
RBM 的上层是不可观测的隐藏层，下层是可观测
的输入层，两层的所有神经元只取 1 或 0，这两个
值分别对应该神经元激活或未激活的两种状态，模
型结构如图 2 所示。
图中 x 表示可见层神经元（输入）；隐藏层神
经元 z 表示输入的映射； ,
,a b W 分别表示可见层偏
置向量、隐藏层偏置向量和权重矩阵。RBM 的能
量函数由下式给出：
j
E x z
,
(
i
a x
i
i
)
b z
j
j
xW z
i
ij
j
（1）
式中 (
E x z 表示能量函数，这种形式使得模
)
,
i
j
型中任意变量的概率可以无限趋于 0 但无法达到 0。
z
b
w
a
x
图 2 受限玻尔兹曼机
Fig.2 Restricted Boltzmann machines
RBM 的联合概率分布由能量函数指定：
P x z
(
,
i
j
)
1
Z
exp(
E x z
,
(
i
))
（2）
j
其中 Z 是被称为配分函数的归一化常数：
Z
exp(
E x z
,
(
i
))
（3）
j
二分图结构特有的性质使 RBM 的条件分布
iP x z 是可因式分解的，使条件分布的
x 和 (
)
| )
|
jP z
(
计算和抽样都比 BM 简单。从联合分布中可以推导
3
胡铭菲等： 深度生成模型综述
出条件分布：
P z
(
j
1|
x
)
1
Z
exp(
b z
j
j
z W x
j
ji
i
)
（4）
根据条件分布因式相乘的原理可将可见变量
的联合概率写成单个神经元分布的乘积：
P z
(
j
P z
(
j
b
sigm(
x
1|
)
P z
(
j
x
0 |
)
j
i
)
x
1|
P z
(
xW
)
i
ij
（5）
1|
x
)
j
训练 RBM 模型使用极大似然法，似然函数的
对数如下表示：
In
L
|
x
In
E x z
,
i
j
e
z
In
e
x z
,
E x z
,
i
j
（6）
2.1.2 配分函数
训练 RBM 时需要计算边缘概率分布，而无向
图模型中未归一化的概率必须除以配分函数进行
归一化，以获得有效的概率分布 ( )P x ：
P x
( )
1
Z
P x
( )
（7）
其中 ( )P x 表示未归一化的概率， Z 表示配分函数。
配分函数是 ( )P x 所有状态的积分，理论上难以求
解。配分函数的计算依赖于模型参数，对数似然关
于模型参数的梯度可以分解为：
P x
log ( ;
)
P x
log ( ;
)
log ( )
Z
（8）
式（8）中的前后两项分别对应训练的正相（positive
phase）和负相（negative phase）。大部分无向图模
型都有计算简单的正相和难以计算的负相，RBM 的
隐藏单元在给定可见单元时是条件独立的，属于典
型的负相，不容易计算。对负相的进一步分析可以
推导出如下结果：
log
Z
E
x P x
~ ( )
P x
log ( )
（9）
式（9）是使用各类蒙特卡洛方法近似最大化似然
的基础。负相涉及从模型分布中抽样，一般被认为
代表了模型不正确的信念，类似人类做梦的过程：
大脑在清醒时经历的真实事件会按照训练数据分
布的梯度更新模型参数，在睡觉时按照模型分布的
负梯度最小化配分函数，然后更新模型参数。但在
RBM 学习中需要交替执行正相和负相的计算才能
完成参数更新。
4
2.1.3 配分函数的估计方法
计算 RBM 的配分函数是训练模型的主要难
点，主要体现为计算困难、计算量大，主要计算方
法可以分为三类，其中对比散度算法以计算量相对
最小、精度尚可而成为 RBM 的主要算法，三类算
法具体如下：
第一类算法是通过引入中间分布直接估计配
分函数的值，中间分布的计算需要使用蒙特卡洛马
尔科夫链或重要性采样，代表算法是退火重要性抽
样算法[18]（Annealed Importance Sampling，AIS）。
AIS 是无向图模型中直接估计配分函数的常用方
法，擅长估计高位空间中复杂分布上的配分函数，
缺点是用蒙特卡洛估计配分函数的方法效率较低。
退火重要性抽样 AIS 通过引入中间分布来缩
小模型分布和数据分布之间的距离，从而估计高维
空间上多峰分布的配分函数。该方法先定义一个已
知配分函数的简单模型，然后估计给定的简单模型
和需要估计模型的配分函数之间的比值，例如在权
重为 0 的 RBM 和学习到的权重之间插值一组权重
不同的 RBM，此时配分函数比值为：
Z
j
Z
j
Z Z
2
Z Z
0
1
（10）
Z
1
Z
n
Z
n
Z
n
Z
1
Z
0
n
1
j
0
1
1
2
1
1
如果对于任意的 0
都能使分布
1
n
j
P 和
j
P
1j
足够接近，则可以用重要性抽样估计每个因子
的值，然后使用这些值计算配分函数比值的估计
值。中间分布一般采用目标分布的加权几何平均：
，考虑到重要性权重，最终的配分函
P
j
j
1
P P
j
1
0
数比值为：
Z
1
Z
0
1 K
（11）
K
k
1
W
k
其中 kW 表示第 k 次抽样时的重要性权重， kW 的值
可从转移算子乘积得到。
第二类计算配分函数的算法是构造新目标函
数替代配分函数，避免直接求解配分函数的过程，
主要包括得分匹配[14]（Score Matching，SM）和噪
声对比估计[16]（Noise Contrastive Estimation, NCE）。
SM 算法精度很高，但缺点是计算量较大，只稍低
于使用 MCMC 采样的 AIS 算法；NCE 算法的精度
一般且计算量也很大，但该算法将无监督学习的似
胡铭菲等： 深度生成模型综述
然函数估计问题转化为学习概率的二值分类问题，
巧妙的避开求解配分函数和估计数据分布的难题，
是一个具有创造性的方法。
得分匹配 得分表示对数概率密度关于模型
参数的导数，SM 算法用模型分布和数据分布的对
数对输入求导后的差的平方代替边缘概率分布作
为 RBM 的新目标函数：
L x
( )
1
2
log
P x
( )
g
x
log
P x
( )
r
x
2
2
（12）
SM 算法的思路与 CD 算法类似，但该算法以
计算量为代价得到更精确的数据概率分布估计。过
大的计算量使 SM 算法通常只用于单层网络或者深
层网络的最下层，另外算法中的求导过程说明该算
法 只 能 应 用 在 连 续 数 据 中 ， 比 率 匹 配 （ Ratio
Matching, RM）将该方法推广到离散数据中[15]。
噪声对比估计 NCE[16]在每个样例中引入类
标签 y ，规定训练数据上的样本属于一类，然后引
入噪声分布，从噪声分布抽样得到的样本属于另一
类，噪声样本和训练样本以及类标签合在一起作为
新的训练样本，在训练过程中指定类先验概率：
P y
(
1)
1
2
（13）
其条件概率可以表示为：
P x y
(
P x y
(
|
|
1)
0)
P x
( )
g
P x
( )
r
（14）
然后用相同方法构造其他类的联合分布。NCE
这种转换的技巧促使了后来生成对抗网络的诞生，
但因为训练困难使该算法更适合随机变量较少的
问题，在给定单词上下文，计算单词的条件概率分
布的任务上获得了很好的效果。
第三类算法是直接估计配分函数关于参数的
近似梯度，这种基于马尔科夫链的近似方法主要包
括对比散度[9]（Contrastive Divergence，CD）、持
续对比散度[12]（Persistent Contrastive Divergen，
PCD ） 和 快 速 持 续 对 比 散 度 （ Fast Persistent
Contrastive Divergen，FPCD）[13]三种。CD 算法是
一种计算量很低的算法，计算效率远高于其他两类
方法，缺点是精度不高，需要使用 MCMC 等算法
精调模型；PCD 算法利用持续马尔科夫链提高 CD
算法的精度；FPCD 用单独的混合机制改善 PCD 的
混合过程，提高算法的训练速度和稳定性。
对比散度 CD 算法在每个步骤用数据分布中
抽取的样本初始化马尔科夫链，有效减少抽样次
5
数、提高计算效率。该算法用估计的模型概率分布
与数据分布之间的距离作为度量函数，首先从训练
样本抽样，利用 n 步 Gibbs 抽样达到平稳分布后再
固定概率分布的参数，从该平稳分布中抽样，用这
些样本计算权重 ,i
jw 的梯度为：
1
l
L
|
ln (
W
i
x S
j
,
x
)= r
P P
g
（15）
其中
S
x
1,
表示训练集，r 表示数据参数，g
,
x
l
表示模型参数。CD 算法是一种近似算法，Perpiñan
等人[10]证明 CD 算法最终会收敛到与极大似然估计
不同的点，因此该算法更适合作为一种计算代价低
的参数初始化方法。Bengio[11]证明了 CD 等价于去
掉最小项的 MCMC 算法，解释了算法中偏差的由
来。
实验显示使用 1 步 Gibbs 抽样的 CD-1 算法就
能得到不错的学习效果。尽管 CD-1 算法的偏差较
大，但可以用于浅层模型的预训练，再把浅层模型
堆叠起来形成深度模型，这个优势也使得快速高效
的 CD 算法成为目前训练 RBM 的标准算法，并用
于 DBN 等深层模型的预训练。
持续对比散度 PCD 算法在应用数学领域被
称为随机最大似然（stochastic maximum likelihood,
SML）算法，是 CD 的一种改进算法，在每个步骤
中用先前梯度步骤的状态值初始化马尔可夫链，有
效提高算法精度，并弥补了 CD 算法无法最大化似
然函数的缺陷。
PCD 用持续马尔科夫链得到负相的近似梯度，
令 t 步的持续马尔科夫链状态为 tx ，则参数的梯度
可以近似为：
P x
ln ( )
E[
xz
T
] E[
x
t k
z
T
t k
]
（16）
每个马尔科夫链在整个学习过程中都在不断
更新，这种做法可以更容易找到模型的所有峰值。
除了计算量比较大以外，PCD 的另一个缺点是超参
数 k 的取值高度依赖于具体问题，如果学习率或训
练时间不合适会使马尔科夫链的遍历性下降进而
产生不稳定的误差。
快速持续对比散度 FPCD 引入了单独的混合
机制以改善 PCD 持续马尔科夫链的混合过程，使
算法性能不会因为训练时间过长等的影响而恶化。
胡铭菲等： 深度生成模型综述
FPCD 使用一组额外的权值 提高样本的混合速
率，原本的权值当作慢速权值 估计数据的期望
值，然后使用混合参数
作为持续马尔科
夫链的更新样本。FPCD 中的快速权重通常使用较
大的学习率并保持足够长的迭代次数，马尔可夫链
改变峰值之后再对快速权重使用权重衰减，促使学
习率收敛到较小的值，从而提高混合速率。
2.1.4 RBM 模型研究进展
基础 RBM 的二值神经元很容易扩展到实值或
向量形式，即高斯-伯努利受限玻尔兹曼机。该模型
假设可见层数据是服从高斯分布的实数用以处理
实值数据，其能量函数可以定义成如下形式：
E x z
( , )
a
z
(
n
i
i
2
2
i
1
i
2
)
n
i
1
j
1
n
xW z
i
i
ij
j
n
（17）
z b
j
j
j
1
根据能量函数得到似然函数和条件概率分布
的过程与二值 RBM 相同。Salakhutdinov[18]利用受
限玻尔兹曼机在高维数据中提取特征的功能，从大
型文本中提取主题，此时可见层神经元服从伯努利
分布。在条件概率的计算中需要归一化指数函数
Softmax 调整概率分布，归一化概率分布并有效避
免数值溢出。
Montufar 等人[19]从理论上证明了 RBM 与[0,1]
之间的任意概率分布的相对熵上界。Sutskever 等人
[20]提出了循环回火 RBM，通过让隐藏层神经元之
间的权重传递更多信息，使模型能容易准确的推断
和更新梯度。Nair 和 Hinton[21]提出用阶梯 S 型神经
元近似替换 RBM 的二值神经元，这种神经元更加
自然地学习光照等自然界变化，提高了模型学习特
征的能力。基于因式分解的三值 RBM[22]将实值图
像映射到因式分解的输出，令隐藏层神经元表示可
见层神经元的协方差和阈值，提高模型对小图形数
据集的识别准确性。
2.2 深度置信网络
深度置信网络[23]（Deep Belief Network，DBN）
的出现使深度学习再次受到人们的关注，缓解了深
度模型很难优化的缺陷，在 MNIST 数据集上的表
现超过当时占统治地位的支持向量机。尽管 DBN
与后来出现的深度生成式模型相比已没有优势，但
它以深度学习历史中里程碑式的重要模型而得到
认可和广泛研究。
2.2.1 DBN 模型结构
置信网络一般是有向图模型，而深度置信网络
6
的最低层具有无向连接边，其它各层之间为有向连
接边。DBN 具有多个隐藏层，隐藏层神经元通常只
取 0 和 1，可见层单元取二值或实数，除顶部两层
之间是无向连接外，其余层是有向边连接的置信网
络，箭头指向可见层，因此 DBN 属于有向概率图
模型，其结构如图 3 所示。
z
2h
1h
x
3W
2W
1W
图 3 深度置信网络结构
Fig.3 The structure of deep belief networks
以 DBN 的前两个隐藏层 1h 和 2h 为例说明模型
结构。此时 DBN 的联合概率分布定义为
2
1
P x h h
( ,
,
P x h W P h h W
(
;
|
1
)
;
)
1
(
;
,
1
2
（18）
2
)
其中
1
W W
{
,
2
}
表示模型参数，
P x h W 表示
(
)
;
|
1
1
有向的置信网络。 1
P h h W 可以用训练 RBM 的
(
)
;
,
2
2
方法预训练，因为可见层和第一个隐藏层的联合分
布与 RBM 的联合概率分布形式相同：
P x h
( ,
1
; )
2
h
P x h h
( ,
,
1
2
; )
（19）
因此 DBN 在训练过程中可以将任意相邻两层
看作一个 RBM。从 DBN 生成样本时，先在顶部隐
藏层内运行几步 Gibbs 抽样，然后按照条件概率由
上至下依次计算各层的值，最后就能得到从 DBN
产生的样本。
2.2.2 DBN 的目标函数
隐藏层 1h 到可见层是有向网络，无法直接得到
隐藏层条件概率，因此假设条件概率的近似分布为
胡铭菲等： 深度生成模型综述
Q h x 。利用 Jensen 不等式可以得到 DBN 的似
1(
)
|
然函数：
P x
log ( )
(
(
1
h
1
h
Q h x
|
1
Q h x
|
1
)log
P x h
( ,
)
1
Q h x
(
|
)
1
H Q h x
P
)log ( )
(
(
|
1
（20）
))
其中
log ( )
P
P h
log (
1
)
log (
P x h
1
|
)
， ( )H 表示熵
函数。该目标函数本质上是 RBM 目标函数的变分
下界。
2.2.3 贪婪逐层预训练算法
随机初始化参数下的 DBN 很难训练，需要使
用贪婪学习算法调整模型参数使模型有容易训练
的初始值。贪婪学习算法采用逐层预训练的方式，
首先训练 DBN 的可见层和隐藏层 1h 之间的参数，
固定训练好的参数并使权重 2W 等于 1W 的转置。在
训练权重 3W 时，从条件概率中抽样获得 2h ，训练
方法与 RBM 的训练方式相同。贪婪逐层预训练算
法提供了两种获得 2h 和 z 的方法，如图 4 所示。
z
2h
1h
x
Q z h
(
|
2
)
Q z x
(
|
)
Q h
(
2
|
h
1
)
Q h
2(
|
x
)
Q h
1(
|
x
)
Q h
1(
|
x
)
z
2h
1h
x
图 4 两种贪恋逐层学习算法
Fig.4 Two kinds of greedy layer-wise pre-training
Q h
(
一种方法是从条件概率 2
|
h 中抽样获得
1
)
2h ，另一种算法直接从条件概率 2(
Q h
|
x 中抽样。
)
使用贪婪算法训练有向概率图时通常使用第二种
方法抽样，因为它在实际应用中表现更好[24]。
7
2.2.4 亥姆霍兹机
DBN 的出现是深度模型的巨大进步，但从数学
的角度推导出变量之间的真实关系需要很大的计
算量，降低了模型的训练速度。Hinton 和 Neal 等人
提出的亥姆霍兹机（Helmholtz Machine，HM）[25]
可以看成是另一种连接形式的 DBN。HM 的基本思
想是保持 DBN 有向性的同时，在层之间增加单独
的权重，使最上层的隐变量可以和可见层进行通
信，能有效提高模型训练速度，HM 模型结构如图
5 所示。
za
P
ha
Q
xa
z
h
x
图 5 亥姆霍兹机
Fig.5 Helmholtz Machine
图 5 展示了全连接网络 HM 中的部分连接，其
中 xa 表示可见层 x 的偏置， ha 和 za 表示两个隐藏层
h 和 z 的偏置，指向向上的实线连接 Q 表示认知权
重，指向向下的虚线 P 连接表示生成权重。Hinton
等人提出了用于训练 HM 的醒睡算法[26]。醒睡算法
将训练过程分为清醒和睡眠两个阶段：清醒阶段是
认知过程，通过真实数据和认知权重由下至上得到
神经元状态，然后用梯度下降调整生成权重；睡眠
阶段是生成过程，通过顶层的特征表示和生成权重
生成底层状态，然后用训练过的生成过程得到的权
值和偏置调节认知权重。
2.2.5 DBN 研究进展
DBN 模型的扩展研究可以归纳为两方面，一方
面是研究如何高效处理大规模无标签数据，更好的
进行无监督学习，另一方面是利用基本的反向传播
等方法微调参数使其获得更好的性能，改动模型结
构以适应更多的应用领域。
Mohamed 等人[27]描述并分析了用连续判别训
练准则优化 DBN 权值等参数的方法，说明基于序
列训练准则学习的 DBN 性能优于原始 DBN。Dahl
等人[28]提出 DBN-HMM 系统用于语音元素识别，
是一种基于 DBN 的隐马尔科夫模型，该模型利用
相关推荐
2023年江西萍乡中考道德与法治真题及答案.doc
2012年重庆南川中考生物真题及答案.doc
2013年江西师范大学地理学综合及文艺理论基础考研真题.doc
2020年四川甘孜小升初语文真题及答案I卷.doc
2020年注册岩土工程师专业基础考试真题及答案.doc
2023-2024学年福建省厦门市九年级上学期数学月考试题及答案.doc
2021-2022学年辽宁省沈阳市大东区九年级上学期语文期末试题及答案.doc
2022-2023学年北京东城区初三第一学期物理期末试卷及答案.doc
2018上半年江西教师资格初中地理学科知识与教学能力真题及答案.doc
2012年河北国家公务员申论考试真题及答案-省级.doc
2020-2021学年江苏省扬州市江都区邵樊片九年级上学期数学第一次质量检测试题及答案.doc
2022下半年黑龙江教师资格证中学综合素质真题及答案.doc
