logo资料库

一种动态分布式约束优化问题协同求解算法.pdf

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：1.02M 资料格式：pdf 举报 版权申诉
第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
资料共13页，剩余部分请下载后查看
    1209647[¹/
    摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 第 26 卷摇 第 9 期摇 摇 2013 年9 月摇 Sep. 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 一种动态分布式约束优化问题协同求解算法* 摇 模式识别与人工智能摇 摇 摇 摇 摇 摇 摇 摇 摇 PR & AI摇 摇 摇 摇 摇 Vol.26摇 No.9 摇 2013 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 摇 葛方振1,2摇 摇 魏摇 臻1摇 摇 陆摇 阳1摇 摇 邱述威1摇 1(合肥工业大学 计算机与信息学院摇 合肥 230009) 2(淮北师范大学 计算机科学与技术学院摇 淮北 235000) 3(北京邮电大学 信息安全中心摇 北京 100876) 摇 李丽香3 摘摇 要摇 多 Agent 协作过程中的许多问题都可在分布式约束优化问题(DCOP) 框架下建模,但多局限于规划问题, 且一般需 Agent 具有完全、准确收益函数. 针对 DCOP 局限性,定义动态分布式约束优化问题(DDCOP),分析求解 它的两个关键操作:Exploration 和 Exploitation,提出基于混沌蚂蚁的 DDCOP 协同求解算法(CA-DDCOP). 该算法借 鉴单只蚂蚁的混沌行为和蚁群的自组织行为,实现Exploration 和Exploitation,根据玻尔兹曼分布,建立平衡Explora鄄 tion 和 Exploitation 的协同方法. 通过多射频多信道无线 Ad Hoc 网络的信道分配验证该算法的有效性. 关键词摇 混沌,协同求解,动态分布式约束优化,信道分配 中图法分类号摇 TP 181 A Collaborative Solving Algorithm for Dynamic Distributed Constraint Optimization Problem GE Fang鄄Zhen1,2, WEI Zhen1, LU Yang1, QIU Shu鄄Wei1, LI Li鄄Xiang3 1(School of Computer and Information, Hefei University of Technology, Hefei 230009) 2(School of Computer Science and Technology, Huaibei Normal University, Huaibei 235000) 3(Information Security Center, Beijing University of Posts and Telecommunications, Beijing 100876) ABSTRACT A large number of problems in the multiagent collaboration process can be modeled under the framework of distributed constraint optimization problem (DCOP). However, DCOP framework is limited to the issue of planning, and the agents in DCOP generally require a complete and accurate reward function. To resolve this issue, a dynamic distributed constraint optimization problem (DDCOP) is defined, and DDCOP忆s crucial operations, exploration and exploitation, are analyzed. Furthermore, a chaotic ant based collaborative solving algorithm for dynamic distributed constraint optimization problem (CA鄄DDCOP) is proposed. The CA鄄DDCOP algorithm is established based on chaotic behavior of a single ant and self鄄organizing behavior of ant colony, thereby the exploration and exploitation are *国家自然科学基金项目(No.61070220, 60873195)、高等学校博士学科点专项科研基金项目(No.20090111110002)、全国博 士学位论文作者专项资金项目(No.200951)、安徽高校省级自然科学研究重点项目(No. KJ2013A229)资助 收稿日期:2012-09-06;修回日期:2012-12-07 作者简介摇 葛方振(通讯作者),男,1975 年生,博士,副教授,主要研究方向为网络与分布式计算. E鄄mail:gfz203377@163. com. 魏臻,男,1965 年生,教授,博士生导师,主要研究方向为分布式控制技术、无线自组织网络. 陆阳,男,1967 年生,教 授,博士生导师,主要研究方向为分布式控制技术、无线自组织网络. 邱述威,男,1975 年生,副教授,博士研究生,主要研究 方向为无线自组织网络. 李丽香,女,1978 年生,副教授,博士生导师,主要研究方向为混沌优化、复杂网络.
    208 模式识别与人工智能摇 摇 摇 26 卷 realized. The proposed algorithm achieves the collaboration of exploration and exploitation according to the Boltzmann distribution. Then a channel allocation in multi鄄radio multi鄄channel Ad Hoc networks is solved by the CA鄄DDCOP algorithm. The simulation results show that the CA鄄DDCOP algorithm performs effectively. Key Words摇 Chaos, Collaborative Solving, Dynamic Distributed Constraint Optimization, Channel Allocation 1摇 引摇 言 分布 式 约 束 优 化 问 题(Distributed Constraint Optimization Problem,DCOP)[1] 是通过多 Agent 协 作,实现资源或任务分配、协同决策的代价最小化或 收益最大化. DCOP 提供了一种表示问题的形式,每 个协作Agent 控制一个或多个变量,多Agent 共同优 化约束. 实际应用中,很多问题可以建模为 DCOP, 如多 Agent 规划协调[2]、 会议安排[3] 和机器人足 球[4] 等. 一般,这类问题的目标是寻找变量最优值. DCOP 全局最优解的求解方法研究已取得很大 进展. 这些方法主要分两类:精确算法和近似算法. 精确算法能确保返回最优解,如异步分布式约束最 优 算 法 (Asynchronous Distributed Constraint Optimization, ADOPT)[1]、最优异步部分交叉算法 (Optimal Asynchronous Partial Overlay, OptAPO)[5]、 分布式伪代码树优化算法(Distributed Pseudotree Optimization Procedure, DPOP)[6]、 无承诺分支定 界 搜 索 算 法 (No鄄Commitment Branch and Bound Search, NCBB)[7]、异步前向边界算法(Asynchronous Forward鄄Bounding Algorithm, AFB)[8]、 多局 部 边 界 搜 索 算 法 (Multiple Local Bounded Search, MULBS)[9],而近似算法是以快速方式找到一个最 好 的 近 似 解, 如 分 布 式 随 机 算 法 (Distributed Stochastic Algorithm, DSA)[10]、最大增益信息算法 (Maximum Gain Message, MGM)[11],随时局部搜索 算 法 (Anytime Local for Distributed Constraint Optimization Problems, ALS_DisCOP)[12]. 然而,精确算法存在一定的局限,即,随着系统设备 (节点) 数目增加,协调开销指数级增长,特别是大 规模应用和复杂场景. 其主要原因在于:1) 精确算 法运行中,需不断重建静态树结构;2) 分布式算法 中,Agent 之间通信导致网络过载;3) 复杂规划或分 配问题通常需处理速度尽可能快,因为尽可能快地 更好;4) 特别是在复杂的情况下 Agent 不知道初始 收益矩阵(Payoff Matrix),必须探索环境,确定不同 得到一个近似解比在不可接受的时间内获得最优解 Search Constraint Optimization 蚁群的自组织行为和作者已提出的自治群集的分布 变量的收益. 所有的收益是依赖于 Agent 的联合行 动,要求 Agent 在探索中认知,如水下机器人( 自主 水下航行器) 测量水下结构[13],无人机测量环境现 象[14],传统 DCOP 算法显 得 无 能 为 力. 这 类 复 杂 DCOP 称 为 动 态 分 布 式 约 束 优 化 问 题(Dynamic Distributed Problem, DDCOP). 因此,一个有效的 DCOP 算法必须解决上 述4 个方面的挑战. 为解决 DDCOP,提出一种新型求解 DDCOP 的 近似算法. 该算法思想基于蚂蚁个体的混沌行为和 式协调算法[15],进一步提出基于混沌蚂蚁的动态分 布式 约 束 优 化 问 题 协 同 求 解 算 法 (Chaotic Ant Based Dynamic Distributed Constraint Optimization Problem, CA鄄DDCOP), 通 过 分 布 式 协 调 实 现 DDCOP 协同求解. 为构建 CA鄄DDCOP 算法,先根据单只蚂蚁的混 沌行为表达式,建立 Agent 对其控制变量数值混沌 选择方法,再根据蚂蚁个体受邻居和信息素作用的 机制,形成动态协调方法,最后根据兰顿蚂蚁表现出 混沌及涌现行为, 且满足玻尔兹曼分布[16], 建立 Agent 对混沌选择值的接受概率, 以体现个体微观 层与群 体 宏 观 层 决 策 之 间 的 关 系. 此 外, 为 验 证 CA鄄DDCOP 算法的有效性,采用此算法解决多射频 多信道无线 Ad Hoc 网络的信道分配问题(Channel Assignment for Multi鄄Radio Multi鄄Channel Wireless Ad Hoc Network, MRMC鄄CA). 2摇 DDCOP 与 DCOP 先分 析 DDCOP 与 DCOP 的 区 别, 然 后 讨 论 DCOP 相关算法,并指出这些算法求解 DDCOP 的局 限性. 同时特别给出两种基于蚂蚁行为的分布式算 法,显示出启发式近似算法求解动态复杂场景的分 布式优化问题的优越性. 2. 1摇 DDCOP 算法 为更清楚理解DDCOP 与DCOP 的区别,下面对
    摇 摇 9 期 两者进行解释. DCOP 由集中式约束优化问题扩展 而来. 在DCOP 中,每个Agent 为它控制的变量赋值, 变量和约束都是分布式、多维自治、可通信的,并给 定一个全局目标函数. 但在 DDCOP 中,很多情况收 益不是先验的,需通过 Exploration 操作获取. Agent 在进行 Exploration 操作同时, 利用当前知识, 进行 Exploitation 操作. 以图 1 为实例分析 DDCOP,变量 x1,x2,x3 分别受控于 Agent a1,a2,a3,x1,x3 是 x2 的 两个邻居,每个变量拥有一个离散域. Exploration 操 作的收益在图1 给出. 图1 中 “?冶 表示将来的、未知 的收益. 由图1 可见,每个 Agent 可为其变量选择一 个数值,实例的总收益依赖于这对 Agent 的变量值, 但约束收益只有在 Exploration 操作之后才能获得. 如当两个 Agent 执行时间步为1 时,总收益是 R1,2 + R2,3 =8 +5 =13. 显然,DDCOP 全局最优解不是最大 化最后收益, 而是最大化在线(Online) 收益. 根据 DDCOP 特点, 基于智能 Agent 的建模方法较为合 适. 因此,采用Agent 作为处理和优化DDCOP 主体, 负责协调和处理它们之间的约束,即每个 Agent 能 处理通信、决策甚至学习. 图1摇 3 个 Agent 的 DDCOP Fig.1摇 A DDCOP for 3 agents 沿用 DCOP 的形式化方法[1], 将 DDCOP 定义 如下. 定义 1摇 动态分布式约束优化问题(DDCOP), DDCOP 可形式化五元组 DP = (X,D,F,A,啄): 1) 变量集合 X = {x1,x2,…,xn n 沂 N}; 2) 离散域集合D ={d1,d2,…,dn n沂N},di 是 变量 xi 的值域; 3)X 的一个具体取值 軇x忆 = {軇x1,軇x2,…,軇xn},軇xi 是 xi 的值,軇x忆 称为一个组态(Configuration). 存在约束 的任一变量组 X忆i 哿 X 对应的局部组态为軇xi忆哿軇x忆,那 么 fi:軇xi忆寅 R 称为组态軇x忆 上的收益函数,即函数 fi(Xi 忆) 表示变量组 X忆i 对应Agent 的联合收益. 收益函数 集合 F = {fi(Xi忆) 坌Xi忆 哿 X}; 4)Agent 集合 A = {a1,a2,…,an n 沂 N},每个 摇 摇 葛方振 等:一种动态分布式约束优化问题协同求解算法 308 Agent 控制一个或几个变量,并为其变量赋值; 变量受控于 Agent,它们之间是双射关系. 足所有函数的和最大(总收益最大),即 fi(Xi忆). 5)啄:A寅 X 为从Agent 到变量的映射关系,表明 在上述关系中,寻找每个变量的值,构成 X*,满 (1) X* = arg max 移坌Xi忆哿X 2. 2摇 DCOP 算法 近些年,已提出几种 DCOP 算法及其变种. 本文 仅概 述 几 个 经 典 算 法, 同 时 指 出 这 些 算 法 求 解 DDCOP 的不足. 异步分布式约束最优算法(ADOPT)[1] 是一种 精确异步 DCOP 算法, 它有 3 个关键思想: 异步搜 索、传播阈值和停止条件. 该算法首先建立深度优先 搜索树,然后异步搜索通过局部视图修改局部变量. 代价信息从底向上传播,数值信息从上向下传,迭代 地紧缩上下界,直到最小代价下界等于其上界时,停 止运行. 通过阈值可有效重新构造以前的部分解,使 最坏 情 况 的 空 间 复 杂 度 限 制 在 多 项 式 级. 然 而, ADOPT 的每个 Agent 根据局部视图修改它的值,可 能导致搜索区域再次被修改,产生指数级冗余信息. 最优异步部分交叉算法(optAPO)[5] 是在调停 者的 干 预 下 直 接 与 约 束 通 信, 局 部 地 集 中 问 题. Agent 为提高局部视图,需增加知识. 当一个 Agent 充当一个调停者,它计算整个问题中的部分解,在调 停过程中,推荐其它 Agent 改变数值. 调停者以集中 式的分枝限界算法,发现局部问题的最优解. 然而, 有时协商 Agent 拒绝共享信息或放弃它们子问题的 决策控制. 分布式伪代码树优化算法(DPOP)[6] 是一种精 确动态规划算法,它采用深度优先树和动态规划求 解全局最优解,主要有3 个阶段:第一阶段是深度优 先树 DFS 形成;第二阶段是自下而上地计算和传播 的代价;第三阶段是由根节点开始,自上而下的数值 传播. 尽管 DPOP 需多项式的运行时间和线性增长 的消息量,但消息大小是指数空间中伪树的宽度. 因 此,过多约束的大量消息限制了该算法的应用. 综上所述,若采用3 种算法及变种解决 DDCOP, 将遭遇静态树不断重建,从而导致放弃搜索边界,再 次开始搜索. 因此,解决 DDCOP,需结构灵活和性能 鲁棒的算法以应对复杂动态的环境. 众所周知,自然界依赖自组织演化,特别是生物 系统的自组织演化. 因此,社会性昆虫的自组织行为 已引起一些学者关注和研究. 社会性昆虫群有成千 上万只个体构成,它们之间没有任何主动的协调. 没
    模式识别与人工智能摇 摇 408 有协调者,个体仅根据局部信息自发协调使整个群 集表现出有序的行为,称为涌现. 涌现的主要特征体 现在群集内部分工的可塑性,从事的各项任务个体 数量的比率能反映内外部环境的变化. 下面,给出基 于蚂蚁行为DDCOP 算法,以表明这些启发式算法对 求解复杂动态问题的优势. 2. 3摇 基于蚂蚁行为的 DDCOP 算法 基于 群 的 广 义 分 配 问 题 算 法(Swarm based Generalized Assignment Problem, Swarm鄄GAP)[17] 是求解复杂分布式任务分配的近似算法. 该算法以 DCOP 建模,基于蚂蚁的分工协作理论设计. 该算法 的协作 Agent 能以低通信和计算代价协调它们的 行为. 基于 蚂 蚁 的 大 团 队 任 务 分 配 (Ant Based Algorithm for Task Allocation in Extreme Teams, eXtreme鄄Ants)[18] 算法受社会性昆虫劳动分工和猎 物协作转运招募过程启发,采用 DCOP 建模. 该算法 利用劳动分工提供快速、高效的决策,采用招募确保 分配的 任 务 并 行 执 行, 有 效 解 决 大 规 模、 动 态 多 Agent 环境的任务分配. 由上述两算法可见,一些启发式算法能有效解 决 DDCOP. 然而,经典的 DCOP 算法由于计算代价 和通信负载而显得无效. 因此,本文试图通过模拟单 适合求解 DDCOP 的算法. 3摇 CA鄄DDCOP 算法 为,然后对它们形式化,并给出 CA鄄DDCOP 算法构 建过程. 3. 1摇 蚁群的混沌和自组织 于这些昆虫群表现出自组织行为和高层的群集结构, 群的能力大于个体之和,而个体功能相对简单.1991 年,Cole[19] 指出,孤立的蚂蚁显示出短暂的、不稳定 的活动, 而蚁群自发产生有规律的 活 动.1991 年, Cole[20] 还报道,单只蚂蚁表现出低维的混沌,而蚁群 具有周期性活动规律.1993 年,Sol佴 等[21] 进一步给出 一个低维混沌映射,形成蚂蚁混沌行为表达式: (2) Z(t + 1) = Z(t)exp{滋[1 - Z(t)]}, 其中, 滋 是控制参数. 文献[22] 指出Cole 的推测,在 动物行为中存在混沌,已暗示个体行为的时空可能 不会因随机世界变化而变化,但依赖于决定性的初 始条件.1995 年,Miramontes[23] 指出,系统中相互作 只蚂蚁的混沌行为和整个蚁群的自组织行为来构建 众多学者关注蚂蚁等社会性昆虫的主要原因在 本节首先简述蚁群中存在的混沌和自组织行 摇 26 卷 用个体当处于混沌到有序的边界状态中,可能存在 最优信息处理能力和最优适应能力. 由相互作用的 混沌个体构成的蚁群能产生有规律的周期性活动. 另外,2009 年,Couzin[24] 提出,蚁群表现出类似神经 的行为,正像移动的神经网络. 因此,上述研究表明单只蚂蚁的混沌行为和整 个蚁群的自组织行为之间存在相互关系,且表现出 一定的行为规律. 本文认为由蚂蚁个体的混沌行为 到有序的宏观行为是一个连续的转换过程,由蚁群 的自组织能力控制. 于是,从某种意义上,可将混沌 和自组织视为求解DDCOP 的一对耦合有效的操作: Exploration 和 Exploitation. 3. 2摇 CA鄄DDCOP 算法 为方便构建算法,先给出一些基本符号描述,然 后形式化混沌和自组织过程. 3. 2. 1摇 基本符号 为表达方便,给出 CA鄄DDCOP 算法中的符号及 表示意义. 假设每个 Agent 控制一个变量,即 Agent ak(1 臆 k 臆 n) 控制 xk,两者对应. 故以下不对 ak 和 xk 区分. 每个Agent 具有一个感知范围 Rs、一个交互 范围 Ri 和一个移动范围 Rm,即Agent ak 可感知到 Rs 内的其它 Agent,可与 Ri 内的其它 Agent 交互通信, 具有移动能力,且 Rm + Ri 臆 Rs. Agent ak 从其值域 dk 选定一数值对其当前数值更新. 值得注意的是, Agent ak 从其值域 dk 选一数值时, 受 Ri 内的其它 Agent 及环境因素(如信息素等) 的影响. 以上 3 个 范围 Rs,Ri,Rm 之间的位置关系如图2 所示. 图2摇 Rs,Ri 和 Rm 之间的位置关系 Fig.2摇 Relations of Rs,Ri and Rm Ri 内节点构成一个图结构,顶点表示 Agent,边 表示一个 Agent 是另一个 Agent Ri 内的邻居,且两 者有约束关系. 軇x =(軇x1,軇x2,…,軇xn) 表示DDCOP 的一 个解组态(Configuration),軇xk(1臆 k臆 n) 表示Agent ak 的值,特别地,軇xl 表示某 Agent Ri 内局部组态. 所 有可能的组态构成组态空间 S. 对于组态軇x 和组态空
    摇 摇 摇 摇 葛方振 等:一种动态分布式约束优化问题协同求解算法 508 的邻域. 祝k(軇x) 9 期 间 S,Agent ak 的邻居定义为 祝k(軇x) 劬 {j 沂 A 颐 j 屹 k,椰Locj - Lock椰 臆 Ri}, 其中,Locj 是 Agent aj 的位置. S 上的邻域系统是一 个集合簇 祝 = {祝k} k沂A,满足下面条件: 1[con(aj) = 軇x(軇xk)] 1)祝k 奂 S; 2)ak 埸 祝k; 3)aj 沂 祝k 当且仅当 ak 沂 祝j,祝k 称为 Agent ak 在当前环境设置下,根据定义1,对式(1) 细化. 定义 2摇 组 态 质 量(Quality of Configuration, QC) 在给定组态軇x 中,Agent ak 的组态质量可定义为 Qk(軇x) = 移j沂祝k(軇x) 摇 摇 (3) 其中,1·是指示函数,祝k(軇x) 是 Agent ak 的邻居集 合, 祝k(軇x) 表示 Agent ak 的邻居数量. 如果 Agent ak 的 軇xk 满足约束 con(aj),那么指示函数值取 1,否 则取0. 定义2 表明局部组态质量反映 Agent ak 的取值 軇xk 满足它与其邻域Agent 之间约束条件越多,式(3) 值越大. 因此,组态 軇x 质量为 Q(軇x) =移軇xk沂軇x (4) Q(軇x)·P(軇x), 因此,DDCOP 就是使其组态质量最大化,即 摇 max移軇x沂S (5) 摇 s. t. 摇 P(軇x) 沂 [0,1],摇 移x~沂S 其中,P(軇x) 所有 Agent 选择组态 軇x 的分布函数. 可 见,DDCOP 最优的组态为 (6) 由式(3) ~ 式(6) 可知,计算组态质量QC 必须计算 每个 Agent 的 组 态 质 量 Qk(軇x ), 而 Qk(軇x ) 需 知 Agent ak 的邻居及其局部组态軇xl. 据上述分析,CA鄄DDCOP 算法的目标是,在约束 条件下,所有 Agent 从各自的值域内选值使它们在 线收益最大. CA鄄DDCOP 算法必须具备 Exploration 和 Exploitation 的分布式协调框架, 以便多个协作 Agent 能够同时执行 Exploration 和 Exploitation. 下 面, 结 合 蚂 蚁 的 混 沌 行 为 和 自 组 织 行 为, 构 建 CA鄄DDCOP 算法. 3. 2. 2摇 混沌行为形式化 因为 多 数 DDCOP 都 是 大 规 模 的 广 义 分 配 (Generalized Assignment Problem, GAP),如分布式 任务分配[17-18] 等. 这些DDCOP 值域都是离散值,需 将连续的混沌低维表达式进行转换,使之满足离散 问题表达需要. 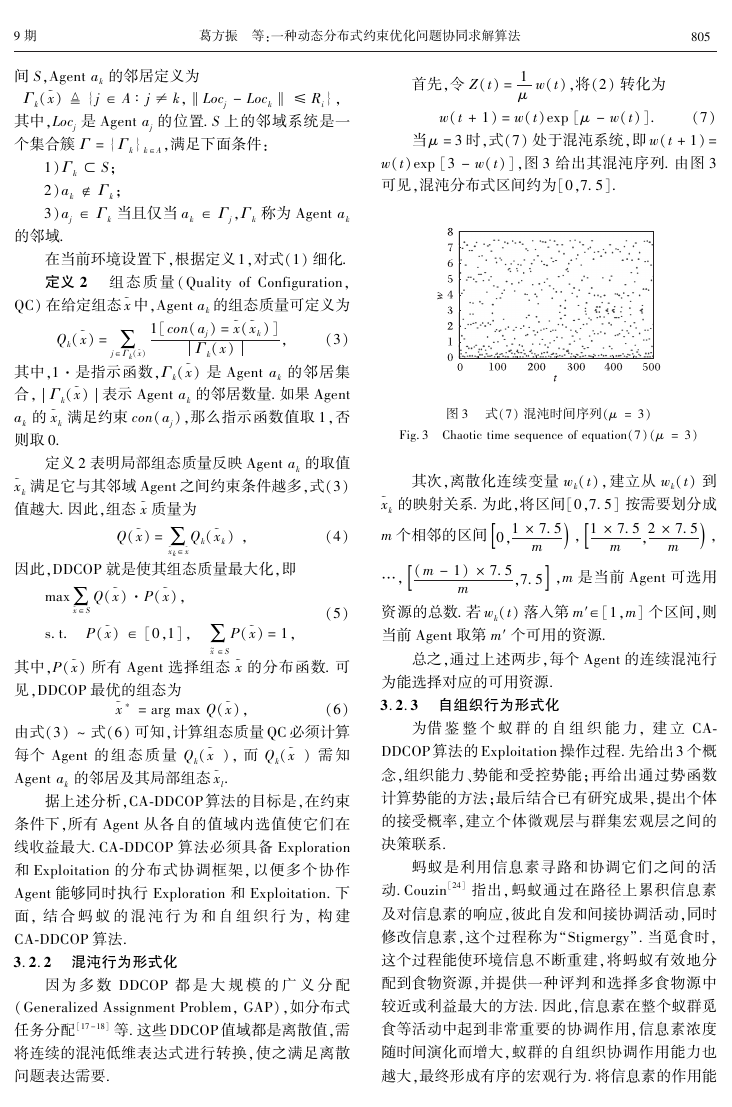軇x* = arg max Q(軇x), P(軇x) = 1, Qk(軇xk) , , 首先,令 Z(t) = 1滋 w(t),将(2) 转化为 (7) w(t + 1) = w(t)exp [滋 - w(t)]. 当 滋 =3 时,式(7) 处于混沌系统,即 w(t + 1) = w(t)exp [3 - w(t)],图3 给出其混沌序列. 由图 3 可见,混沌分布式区间约为[0,7.5]. 图3摇 式(7) 混沌时间序列(滋 = 3) [ m Fig.3摇 Chaotic time sequence of equation(7)(滋 = 3) 其次,离散化连续变量 wk(t),建立从 wk(t) 到 軇xk 的映射关系. 为此,将区间[0,7.5] 按需要划分成 , 1 伊 7.5m ,2 伊 7.5 m 个相邻的区间 0,1 伊 7.5 [ )m )m [ , …, (m - 1) 伊 7.5 ]5 ,m 是当前 Agent 可选用 ,7. 资源的总数. 若 wk(t) 落入第 m忆沂[1,m] 个区间,则 当前 Agent 取第 m忆 个可用的资源. 总之,通过上述两步,每个 Agent 的连续混沌行 为能选择对应的可用资源. 3. 2. 3摇 自组织行为形式化 为借 鉴 整 个 蚁 群 的 自 组 织 能 力, 建 立 CA鄄 DDCOP 算法的Exploitation 操作过程. 先给出3 个概 念,组织能力、势能和受控势能;再给出通过势函数 计算势能的方法;最后结合已有研究成果,提出个体 的接受概率,建立个体微观层与群集宏观层之间的 决策联系. 动. Couzin[24] 指出,蚂蚁通过在路径上累积信息素 及对信息素的响应,彼此自发和间接协调活动,同时 修改信息素,这个过程称为“Stigmergy冶. 当觅食时, 这个过程能使环境信息不断重建,将蚂蚁有效地分 配到食物资源,并提供一种评判和选择多食物源中 较近或利益最大的方法. 因此,信息素在整个蚁群觅 食等活动中起到非常重要的协调作用,信息素浓度 随时间演化而增大,蚁群的自组织协调作用能力也 越大,最终形成有序的宏观行为. 将信息素的作用能 蚂蚁是利用信息素寻路和协调它们之间的活
    模式识别与人工智能摇 U{k,j}(軇xk,軇xj). 608 力称为组织能力(Organizational Capacity),对所有 蚂蚁的活动起到关键导向作用,且它随时间演化而 增强. 势能是 Agent 的邻居对其影响的度量. 若再加 上信息素组织能力影响后,称为受控势能. 计算 Agent(蚂蚁) 势能的方法. 对于给定组态 軇x,势函数 UAl颐 Al 奂軇x 表示在组态空间 S 的相互作用, 其中 UAl颐 軇x寅 R,Al 是一个 Ri 内Agent(蚂蚁) 构成的 团(Clique). 势函数 UAl(軇xAl) 仅依赖 軇xAl = {軇xk颐 k沂Al}. 令 j,k沂Al(j,k = 1,2,…,n, j 屹 k) 是两个Agent,于 是 Agent ak 选择 軇xk 对应的局部势能 着 k(軇xk) 为 着 k(軇xk,軇xj沂祝k) = 移k沂Al,Al哿S U(Al) = U{k}(軇xk) + 移j沂祝k 计算受控势能 椎 数学模型如下: (9) 摇 摇 摇 yk(t) = yk(t - 1)(1 +rk), 摇 摇 着 k(軇xk,軇xj沂祝k) 摇 椎k(軇xk,t) = (10) 摇 摇 摇 摇 yk(t) 式(9)、(10) 用来计算 Agent ak 在信息素和它 的邻居作用下的受控势能. 椎k(軇xk,t) 为Agent ak 在 t 步的受控势能. 式(9) 为连续的减函数, 是式(10) 中的分母项,表达信息素组织能力随信息素浓度增 大而增强,即自组织能力对单个 Agent 控制能力越 强. 故 yk(t) 是Agent ak 当前步的组织变量,令 yk(0) = 0.999. rk 为 Agent ak 的组织因子,它影响式(10) 的收敛速度,若 rk 较大,收敛较快,反之,收敛较慢. 因此,rk 可根据具体问题设定,一般地0臆 rk 臆0.5. 考虑到 Agent 之间的自组织能力的差别,可采用随 机函数设置,如 rk =0.02 + 0.4·rand(1). 为便于理 解,以 rk =0.01 + 0.2·rand(1) 为例,给出自组织能 力演化图,如图4 所示. (8) . 摇 摇 26 卷 Hamann 等[16] 指出,Langton 蚂蚁系统满足玻尔兹曼 分布式. 依据该研究成果,所有 Agent 可根据局部组 态軇xl 同时更新它们的混沌选择数值. 祝k(軇x) 是Agent ak 根据 其 约 束 可 选 择 的 数 值 集 合. 具 体 地,軇xk 为 Agent ak 在 t 步的数值,軇yk 为Agent ak 在 t + 1 步的可 选数值. Agent ak 从軇xk 到軇yk 的接受概率: exp[ - 椎(軇yk,軇xl(Al\k))] Pk(軇xk,軇yk 軇xl) = k沂祝k( x~)exp[ - 椎(軇xk,軇xl(Al\k))], 移x~ (11) 其中,Al\k 为 Rs 范围内除 Agent ak 的所有 Agent 的 集合,即 Al\k = {r 沂 Al 颐 r 屹 k};(軇yk,軇xl(Al\k)) 表示 Agent ak 选择 軇yk, 而 其 它 Agent 选 择 軇xl(Al\k). (軇xk, 軇xl(Al\k)) 的含义与(軇yk,軇xl(Al\k)) 类似. CA鄄DDCOP 算法通过下面方式更新 Agent 的组 态 軇x =(軇x1,軇x2,…,軇xn):将式(9)、(10) 中的受控势能 椎 代入式(11),可得Agent 选择各个值的条件概率. 若第 t 次迭代的组态 軇x t = (軇x t n),则第 t + 1 次迭代中对任意一个 k(k = 1,2,…,n),依据条件概 率 Pk(軇xk 軇x(t+1) k-1 ,軇x t ,…,軇x(t+1) n) 在组态空间 1 中选择軇x(t+1) . 通过多次信道选择后,所有的Agent 将 选择较低势能的信道组态,也就是具有较高收益的 信道选择结果. 3. 2. 4摇 CA鄄DDCOP 算法过程 2,…,軇x t 1,軇x t k+1,…,軇x t 考虑 DDCOP 动态移动的因素,如无人机等,假 设 Rs 逸 Ri + Rm 隐含了位于 Loc(k,t) 的Agent ak 能 够评估它的新邻居,因为当它移动到 Loc(k,t + 1) 沂 祝k 后,Ri 内的其它 Agent 没有变化,依然在感知 范围 Rs 之内. 即, 算法运行中, 相邻两次 迭 代 需 Agent 位置信息能被感知到, 确保算法并行运行. CA鄄DDCOP 算法过程如下所示. 算法 1摇 CA鄄DDCOP 算法 输入 摇 初始化参数 Rm,Ri,Rs,最大迭代次数 T,当前迭代 t = 1,Agent 数量 n 输出 摇 最优或次优组态 While(t < = T) k 采用蚂蚁混沌行为产生 Agent ak 的选择值 軇yk; 产生 Agent 的交互范围 祝s(軇x) 劬 {k 沂 A颐 k 屹 s,椰Lock - Locs椰 臆 Ri}; For each Agent ak 沂 祝s(軇x) 采用式(8) 评估 着 k(軇xk,軇xj沂祝k),采用式(11) 计算 P(軇xk,軇yk | 軇xl); 驻椎 = 椎(軇yk) - 椎(軇xk); If 驻椎 < 0 軇xk = 軇yk; Else 图4摇 yk(t) 随时间演化过程 Fig.4摇 Time evolution process of yk(t) 最后,计算 Agent 混沌选择数值的接受概率.
    9 期 摇 摇 摇 摇 葛方振 等:一种动态分布式约束优化问题协同求解算法 将 N 个节点的一个策略方案作为一个策略组态, 称为策略向量,向量的第 i 列对应节点 i 的策略 gi. g = (g1,g2,…,gN) = (gi) i沂N 所有可能的策略组态集合 GC = {(gi) i沂N gi 沂 GCi,坌 沂 N}. 对任何策略组态 g =(gj) j沂N 和任何 i沂 N,g -i = m 708 的受控势能,通过接受概率判断混沌选择的信道是 否被接受,随后算法以迭代方式运行;最后,为保证 算法的动态性,设计一种动态同步机制,并描述信道 分配算法. 4. 2. 1摇 混沌选择信道 对节点 i,根据式(7) 计算 wk(t). 将信道集合 C 按编号索引,形成序列 c1 刍 c2 刍…刍 cn,并分成 Ci 和 Ci 两类,Ci ={c kic =1,坌c沂 C} 表示节点 i 分配 射频的信道集合,Ci = C\Ci 表示待分配的信道. 令 Ci = m,将区间[0,7.5] 按需要划分成 m 个相邻 的 区 间 [0, 1 伊 7.5m ), [1 伊 7.5m , 2 伊 7.5m ),…, [(m - 1) 伊 7.5 ,7.5]. 若 wk(t) 落入第 m忆沂[1,m] 个区间,则当前节点 i 取第 m忆 个可用的信道. 这样, 每个节点通过连续混沌行为能选择可用信道. 4. 2. 2摇 计算节点势能 为计算节点的势能,需计算信道已使用的带宽 比、信道冲突损失和信道切换时延. 首先,量化信道已用带宽比. 节点采用 802.11 的虚拟载波监听机制,可根据 NAV 值得到信道被占 用的时间. 在感知阶段 TSS,每个节点以感知时间周 期 TSRate 进行采样监视信道. 信道状态有“ 忙冶 和 “ 闲冶 两 种 状 态. Ti,busy(c) 为 感 知 到“ 忙冶 时 间, Ti,idle(c) 为感知“ 闲冶 时间. 因此, 在感知阶段结束 时,节点 i 感知到信道 c 的已用带宽比 Ti,busy(c) + Ti,idle(c) (12) 其次,评估信道冲突带宽损失. 每个网络节点选 定一个信道,不仅需要式(12) 的信道负载,且需来 自邻居节点的内部干扰. 令 Kic 表示已被节点 i 分配 到信道 c沂 C 上的接收射频 R 的数量,Kic 沂{0,1}. 具体地,节点 i 的信道分配策略 gi 定义为 gi = (Ki1,Ki2,…,Ki C )T, 节点 i 的策略 gi 是所有信道分配给射频的方案. 节 点 i 使用的接收射频 R 的数量 Bi,neig(c) = Ti,busy(c) . Ki =移C 摇 j =1 Kij . If rand[0,1] < P(軇xk,軇xk 軇xl) End If 軇xk = 軇yk; End If End For t = t + 1; End While 由算法流程可看出,每个 Agent 通过混沌行为 获得一个数值,该数值是否被接受取决于邻居和信 息素的联合作用,经过 T 次协调,所有 Agent 会趋于 最优和次优组态. 4摇 MRMC 信道分配问题 为验证 CA鄄DDCOP 算法性能,采用 CA鄄DDCOP 算法解决多射频多信道(Multi鄄Radio Multi鄄Channel, MRMC) 无线Ad Hoc 网络的信道分配问题(Channel Assignment,CA). 在实际应用中, 无线网络引入多 射频多信道架构的是减少无线干扰,提高网络性能. 但如何设计一种智能的信道分配算法,将每个节点 的可用信道映射到射频, 是一个挑战性问题. 因为 MRMC 网络中, 多个射频在不同信道上工作, 只有 两相邻节点拥有相同信道才可相互通信. 假设网络 所有节点都有相同数量的射频,由鸽巢原理可知,当 可用信道数小于每个节点射频数的 2 倍时,无论如 何分配信道,都可保证网络连通;否则,就需设计信 道分配算法,确保网络连通. 不然会造成网络分割, 降低网络覆盖. 为此, 先对 MRMC鄄CA 问题描述, 再详细阐述 CA鄄DDCOP 算法求解 MRMC鄄CA 问题,最后给出仿 真实验结果. 4. 1摇 MCMR鄄CA 问题描述 很多信道分配方法仅考虑静态的内部干扰,如 采用冲突图描述网络不同链接间的干扰关系[25],不 能处理外部干扰,但可通过周期刷新分配方案,将静 态信道分配方法扩展成动态分配方法[26]. 本文根据 文献[27],考虑邻居节点之间的内部干扰、 外部干 扰和节点间信息的不完整性, 采用 CA鄄DDCOP 算 法,设计一种动态干扰感知的信道分配算法,为每个 射频分配合适的信道. 4. 2摇 应用 CA鄄DDCOP 算法 CA鄄DDCOP 算法的目标是在信道分配过程中, 减少Ad Hoc 网络内部、同一地点环境和其它无线干 扰的影响. 算法实现过程. 节点先通过混沌行为将它 的信道进行分配;再计算节点的局部信道分配组态
    808 (gj) j沂N\i 是除节点 i 之外所有节点的策略组态. 反过 来,给定 g -i =(gj) j沂N\i 和 gi,(gi,g -i) 则是一个策略 组态 g = (gi) i沂N. 注意节点 i 可能不完全知道 g -i. Ni 表示节点 i 的干扰域内节点数,Ri(c) 表示集合 Ni 中 在给定时间内调整它们的接收射频 R 到信道 c 上的 节点数: Ri(c) =移j沂Ni Kjc . 模式识别与人工智能摇 摇 摇 26 卷 接收射频 R 的信道. Hello 消息发送时机. 当一个新节点加入网络或 当一个节点停止从其邻居接收 Hello 消息时, 该节 点要发送 Hello 消息,通报所有可用信道. 一旦一个 节点已知其一跳邻居的接收射频 R 的信道,节点切 换到这些信道的发送射频 T,并每隔时间 TH 发送一 次 Hello 消息. 数据传输. 一个节点从邻居节点收集信息之后, 就可传输数据. 节点可采用不同信道向不同邻居节 点发送信息. 设每个信道有一个数据包队列,数据包 根据接收邻居的信道加入相应的队列. 当发送射频 T 切换到每个信道,开始发送所有或部分相应队列 的数据包. 发送控制. 每个节点采用随机方式访问所有需 要发送数据的信道. 当信道切换之后,发送射频 T 在 该信道的最大时间为 Tmax,即发送时间最大为 Tmax. 发送射频 T 切换时延为常数 Ds. 发送射频 T 切换. 当节点切换到新的信道可能 导致它与邻居的 CTS/RTS 失效. 因此,为避开这种 失效引起的冲突,在节点切换到新的信道之后,等待 Dt 个时间单位. 接收射频 R 切换. 切换接收射频 R 到任何信道 前,必须通过Hello 消息通知其邻居. Hello 消息包括 两部分内容:目标信道和切换定时器 TS,TS 通常比 TH 大,设 TS 稍微大于2TH. 节点同步机制过程. 由于Ad Hoc 网络的业务是 随机的、突发性的,所以网络中各个节点的信道损失 函数值是时刻变化的. 某些信道会因数据流量的增 大而变得拥塞,有些信道因传输数据结束而空闲. 因 此,需要节点周期性地监测各自信道损失函数值 Mi(c,g -i),当 Mi(c,g -i) 大于给定的阈值,开始执行 表2 的 MRMC鄄CA 步骤,为每个节点获得合适的信 道. 然后按下列步骤同步机制执行: 1) 节点 i 有数 据发送,先发送 Hello 消息,进入一个时间周期 Dt, 为发送数据做准备; 2) 节点 i 的切换发送射频 T 到 该信道,等待 Dt,才能开始数据发送; 3) 节点 i 发送 数据包时间至多 Tmax,然后切换发送射频 T 到另一 信道,开始另一信道的数据传输过程,直到该 TH 状 态结束; 4) 当节点 i 需接收数据时,先发送Hello 消 息,再切换接收射频到其信道. 4. 2. 4摇 MRMC鄄DDCOP 问题求解过程 每个节点视为 CA鄄DDCOP 中的一个 Agent. 将 损失函数式(13) 看作Agent 之间的势能. 于是,根据 CA鄄DDCOP 算法,给出MRMC鄄CA 问题求解过程,如 下所示. . 2 于是,Ri(C) / Ni 称为信道 c 上干扰节点的浓度,即信 道 c 上的冲突节点占干扰域内节点的比率. 这样节 点 i 以信道已用比和信道冲突比的平均值作为带宽 损失: Mi,B(c,g -i) = Bi,neig(c) + Ri(c) / Ni 然而,节点的决策代价不仅依赖于所选信道的 可用带宽,且还考虑切换时延惩罚. 根据文献[26], 802. 11 需考虑切换时延,通常为10 滋s ~ 80 滋s. 在射 频切换频率时,较长的切换时延影响协议的性能. 考 虑切换时延与Hello 消息间隔 TH 的关系,如果 TH 足 够大,切换时延就可忽略不计;相反,较长的切换时 延就应考虑更高的代价,使节点少切换信道. 设节点 i 使用信道 ci,任何信道 c 的切换时延损失函数为 Mi,D(c,g -i) = { Ds TH,摇 c 屹 ci 0, otherwise 最后,节点 i 选择信道 c 的损失函数是带宽和切 换时延损失之权重和: Mi(c,g -i) = 酌Mi,B(c,g -i) + (1 - 酌)Mi,D(c,g -i), (13) 其中,酌 是权重调节参数,酌 沂 [0,1]. 这样,Mi 表示 节点 i 的损失矩阵,矩阵的行表示节点 i 的策略(即, 信道选择的策略), 列是其它 Agent 所有的可能策 略 g -i. 这里,用信道损失 Mk(c,g -k) 代替式(8) 中的 势能 着 k(軇xk,軇xj沂祝k). 依据 CA鄄DDCOP 算法原理,经过 多次信道选择之后,所有 Agent 将选择具有较低损 失函数的信道组态,也就得到了具有较高目标函数 值的信道组态. 4. 2. 3摇 节点同步机制 求解 MRMC鄄CA 问题,本文是采用信息交互方 式使所有节点之间同步,而不是采用专用信道控制. 由于每个节点分配一个不同的信道到接收射频 R, 网络拓扑结构可能会被分割. 为避免网络分割,节点 必须能感知到它邻居节点的接收射频 R 使用的信 道,并通过广播 Hello 消息向它邻居节点通报它的
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料