2014年重庆大渡口中考数学真题及答案B卷.doc-资料库

第1页 / 共11页

第2页 / 共11页

第3页 / 共11页

第4页 / 共11页

第5页 / 共11页

第6页 / 共11页

第7页 / 共11页

第8页 / 共11页

2014 年重庆大渡口中考数学真题及答案 B 卷参考公式:抛物线 y＝ax2＋bx＋c(a≠0)的顶点坐标为（满分：150 分时间：120 分钟） b 2 4, ac  4 a (  b 2 a ) ,对称轴公式为 x  b 2 a . 一、选择题：（本大题共 12 个小题，每小题 4 分，共 48 分） 1、某地连续四天每天的平均气温分别是：1℃，－1℃，0℃，2℃，则平均气温中最低的是（） A、－1℃ B、0℃ C、1℃ D、2℃ 2、计算 2 x 5 x 的结果是（） 2 2 A、3 B、3x C、 23x D、 43x 3、如图，△ABC∽△DEF，相似比为 1：2，若 BC＝1，则 EF 的长是（） A、1 B、2 C、3 D、4 4、如图，直线 AB∥CD，直线 EF 分别交 AB、CD 于点 E、F，若∠AEF＝50°，则∠EFC 的大小是（） A、40° B、50° C、120° D、130° 5、某校将举办一场“中国汉字听写大赛”，要求各班推选一名同学参加比赛。为此，初三（1）班组织了五轮班级选拔赛，在这五轮选拔赛中，甲、乙两位同学的平均分都是 96 分，甲的成绩的方差是 0.2，乙的成绩的方差是 0.8，根据以上数据，下列说法正确的是（） A、甲的成绩比乙的成绩稳定 B、乙的成绩比甲的成绩稳定 C、甲、乙两人的成绩一样稳定 D、无法确定甲、乙的成绩谁更稳定 6、若点（3，1）在一次函数 y  kx  2( k  的图象上，则 k 的值是（） 0) A、5 B、4 D、1 7、分式方程 4 1x  B、 A、 1x   C、3 3 x 1 x   的解是（）

C、 3x  D、 3 x   8、如图，在矩形 ABCD 中，对角线 AC、BD 相交于点 O，∠ACB＝30°，则∠AOB 的大小为（） A、30° B、60° C、90° D、120° 9、夏天到了，某小区准备开放游泳池，物业管理处安排一名清洁工对一个无水的游泳池进行清洗。该工人先只打开一个进水管，蓄了少量水后关闭进水管并立即进行清洗，一段时间后，再同时打开两个出水管将池内的水放完，随后将两个出水管关闭，并同时打开两个进水管将水蓄满。已知每个进水管的进水速度与每个出水管的出水速度相同。从工人最先打开一个进水管开始，所用的时间为 x，游泳池内的蓄水量为 y，则下列各图中能够反映 y 与 x 的函数关系的大致图象是（） 10、下列图形都是按照一定规律组成，第一个图形中共有 2 个三角形，第二个图形中共有 8 个三角形，第三个图形中共有 14 个三角形，……，依此规律，第五个图形中三角形的个数是（） A、22 B、24 C、26 D、28 11、如图，菱形 ABCD 的对角线 AC、BD 相交于点 O， AC＝8，BD＝6，以 AB 为直径作一个半圆，则图中阴影部分的面积为（） A、 25 C、 25 6 6  6 B、 25 2 D、 25 8  6  6 12、如图，正方形 ABCD 的顶点 B、C 在 x 轴的正半轴上，

反比例函数 y  ( k  在第一象限的图象经过顶点 0) k x A（m，2）和 CD 边上的点 E（n， 2 3 ），过点 E 的直线l 交 x 轴于点 F，交 y 轴于点 G（0，－2），则点 F 的坐标是（） A、 5( 4 ,0) B、 7( 4 ,0) C、 9( 4 ,0) D、 11( 4 ,0) 二、填空题：(本题共 6 小题，每小题 4 分，共 24 分，) 13、实数 12 的相反数是。 14、函数 y  1  x 2 中，自变量 x 的取值范围是。 15、在 2014 年重庆市初中毕业生体能测试中，某校初三有 7 名同学的体能测试成绩（单位：分）如下：50，48，47，50，48，49，48。这组数据的众数是。 16、如图，C 为⊙O 外点，CA 与⊙O 相切，切点为 A，AB 为⊙O 的直径，连接 CB。若⊙O 的半径为 2，∠ABC＝60°，则 BC＝。 17、在一个不透明的盒子里装有 4 个分别标有数字 1，2，3，4 的小球，它们除数字不同其余完全相同，搅匀后从盒子里随机取出 1 个小球，将该小球上的数字作为 a 的值，则使关于 x 的不等式组  1 2 x a      2 x a  只有一个整数解的概率为。 18、如图，在边长为 6 2 的正方形 ABCD 中，E 是 AB 边上一点，G 是 AD 延长线上一点，BE ＝DG，连接 EG，CF⊥EG 于点 H，交 AD 于点 F，连接 CE、BH。若 BH＝8，则 FG＝。三、解答题：（本大题共 2 个小题，每小题 7 分，共 14 分） 19、计算： ( 3)  2    2 2014 0  9 (  11 )  2

20、如图，在△ABC 中，CD⊥AB，垂足为 D。若 AB＝12，CD＝6， tan A  ，求sin 3 2 B  cos B 的值。四、解答题：（本大题共个 4 小题，每小题 10 分，共 40 分） 21、先化简，再求值： ( x 1   3  ) 1 x  2 x 4  x 4 x  1  ，其中 x 是方程 x  x 1  2 2  5  的解。 0 22、重庆市某餐饮文化公司准备承办“重庆火锅美食文化节”。为了解市发对火锅的喜爱程度，该公司设计了一个调查问卷，将喜爱程度分为 A（非常喜欢）、B（喜欢）、C（不太喜欢）、 D（很不喜欢）四种类型，并派业务员进行市场调查。其中一个业务员小丽在解放碑步行街对市民进行了随机调查，并根据调查结果制成了如下两幅不完整的统计图。请结合统计图所给信息解答上列问题：（1）在扇形统计图中 C 所占的百分比是；小丽本次抽样调查的为数共有人；请将折线统计图补充完整；（2）为了解少数市民很不喜欢吃火锅的原因，小丽决定在上述调查结果中从“很不喜欢” 吃火锅的市民里随机选出两位进行电话回访，请你用列表法或画树状图的方法，求所选出的两位市民恰好都是男性的概率。 23、某生态往市区以让市民农业园种植的销售外，还亲自去生态青椒除了运可农业

园购买。已知今年 5 月份该青椒在市区、园区的销售价格分别为 6 元/千克、4 元/千克，今年 5 月份一共销售了 3000 千克，总销售额为 16000 元。（1）今年 5 月份该青椒在市区、园区各销售了多少千克？（2）6 月份是青椒产出旺季，为了促销，生态农业园决定 6 月份将该青椒在市区、园区的销售价格均在今年 5 月份的基础上降低 %a ，预计这种青椒在市区、园区的销量将在今年 5 月份的基础上分别增长 30%、20%，要使得 6 月份该青椒的总销售额不低于 18360 元，则 a 的最大值是多少？ 24、如图，在△ABC 中，∠ACB＝90°，AC＝BC，E 为 AC 边的中点，过点 A 作 AD⊥AB 交 BE 的延长线于点 D，CG 平分∠ACB 交 BD 于点 G，F 为 AB 边上一点，连接 CF，且∠ACF＝∠CBG。求证：（1）AF＝CG；（2）CF＝2DE 五、解答题：（本大题共 2 个小题，每小题 12 分，共 24 分）

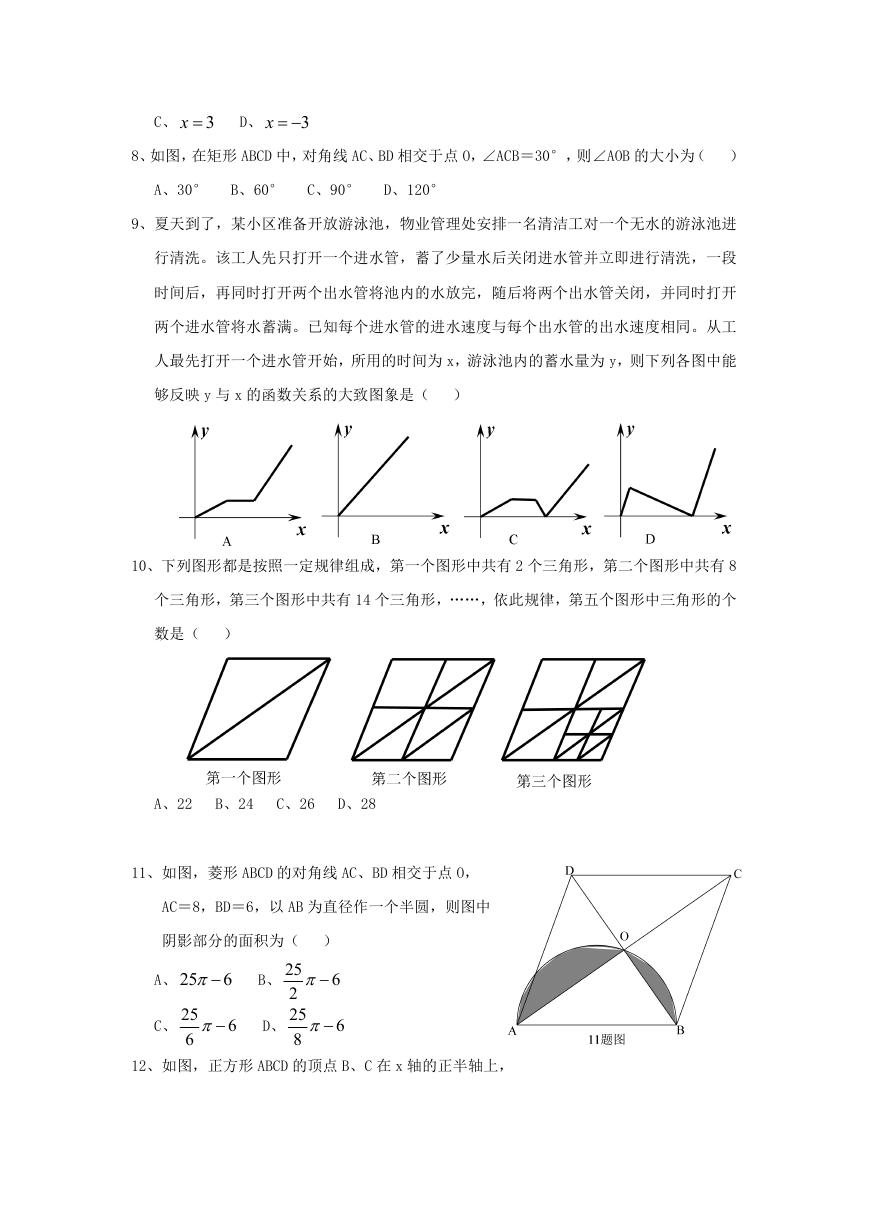
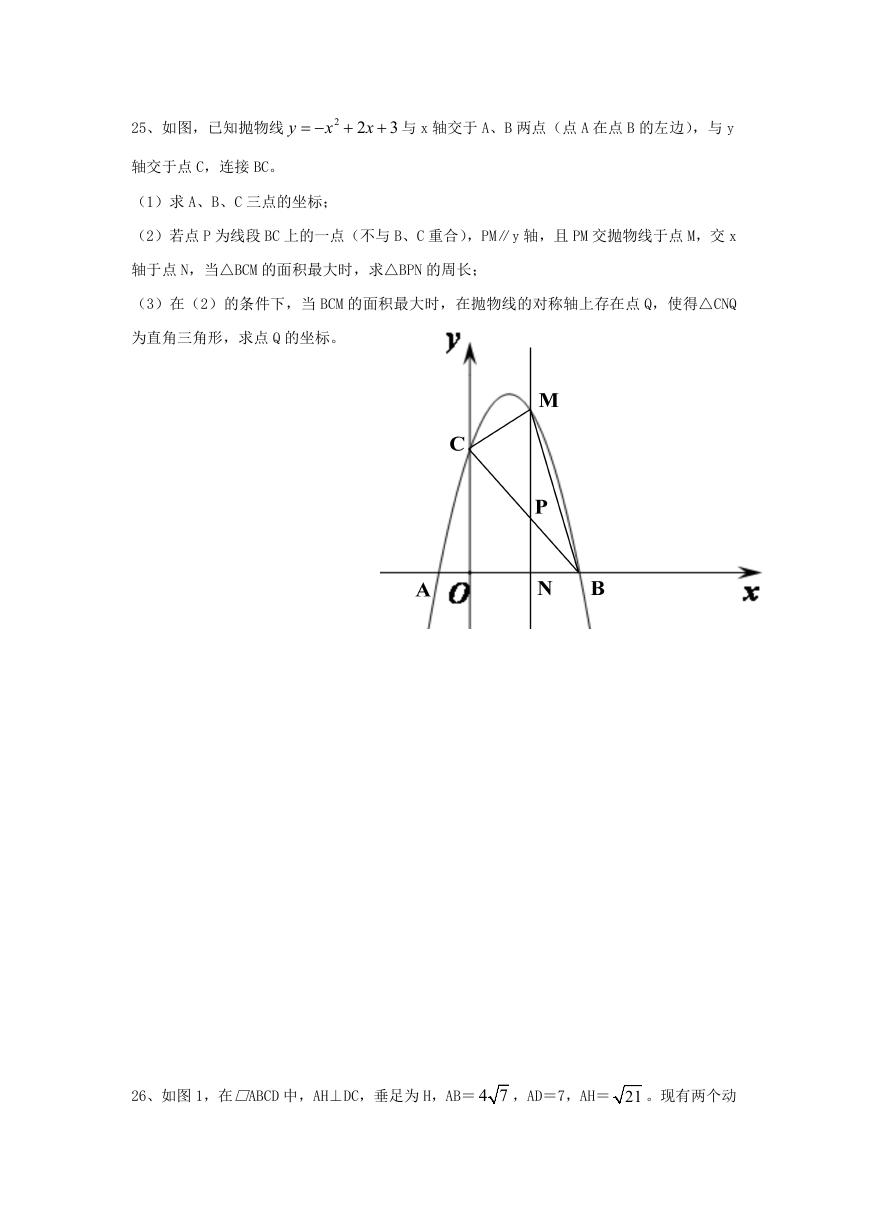
25、如图，已知抛物线 y   x 2  2 x  与 x 轴交于 A、B 两点（点 A 在点 B 的左边），与 y 3 轴交于点 C，连接 BC。（1）求 A、B、C 三点的坐标；（2）若点 P 为线段 BC 上的一点（不与 B、C 重合），PM∥y 轴，且 PM 交抛物线于点 M，交 x 轴于点 N，当△BCM 的面积最大时，求△BPN 的周长；（3）在（2）的条件下，当 BCM 的面积最大时，在抛物线的对称轴上存在点 Q，使得△CNQ 为直角三角形，求点 Q 的坐标。 26、如图 1，在□ABCD 中，AH⊥DC，垂足为 H，AB＝ 4 7 ，AD＝7，AH＝ 21 。现有两个动

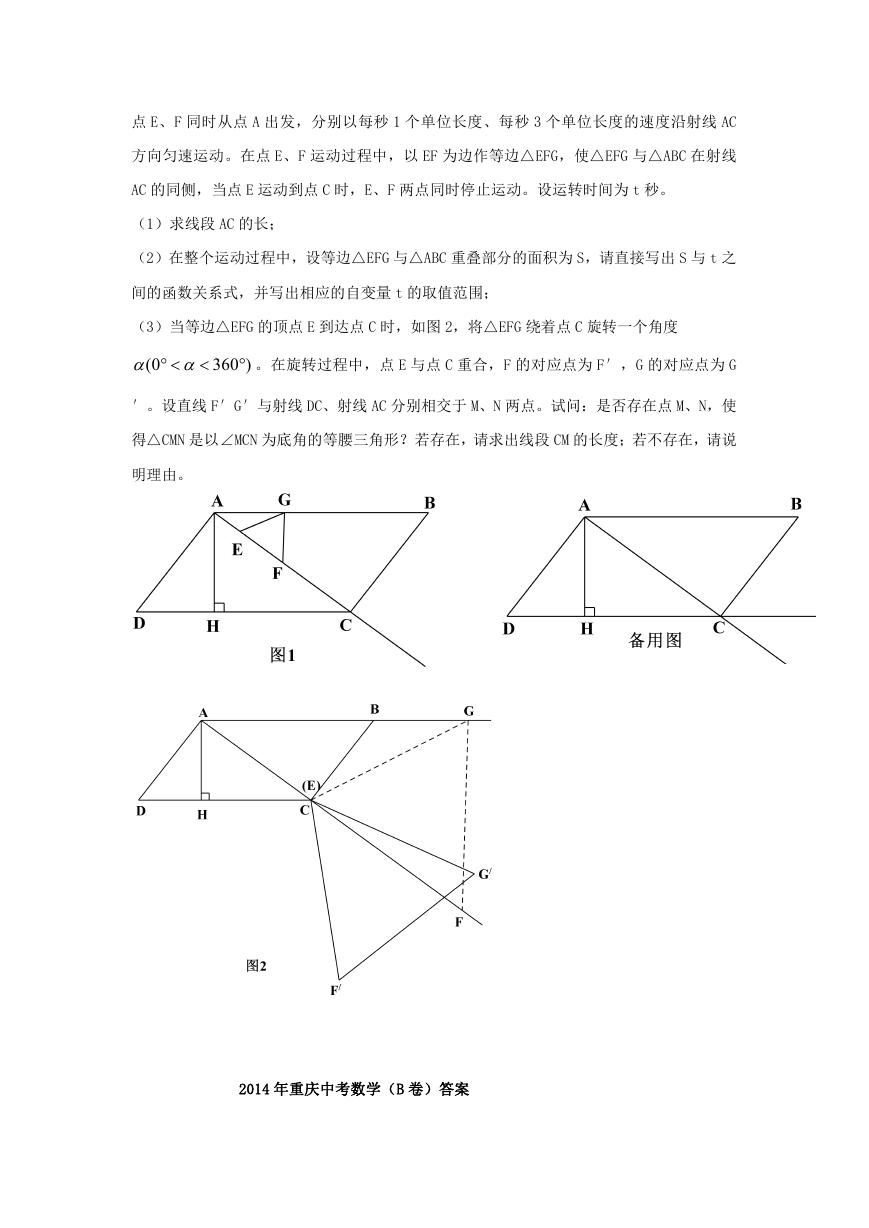
点 E、F 同时从点 A 出发，分别以每秒 1 个单位长度、每秒 3 个单位长度的速度沿射线 AC 方向匀速运动。在点 E、F 运动过程中，以 EF 为边作等边△EFG，使△EFG 与△ABC 在射线 AC 的同侧，当点 E 运动到点 C 时，E、F 两点同时停止运动。设运转时间为 t 秒。（1）求线段 AC 的长；（2）在整个运动过程中，设等边△EFG 与△ABC 重叠部分的面积为 S，请直接写出 S 与 t 之间的函数关系式，并写出相应的自变量 t 的取值范围；（3）当等边△EFG 的顶点 E 到达点 C 时，如图 2，将△EFG 绕着点 C 旋转一个角度    (0  360 )  。在旋转过程中，点 E 与点 C 重合，F 的对应点为 F′，G 的对应点为 G ′。设直线 F′G′与射线 DC、射线 AC 分别相交于 M、N 两点。试问：是否存在点 M、N，使得△CMN 是以∠MCN 为底角的等腰三角形？若存在，请求出线段 CM 的长度；若不存在，请说明理由。 2014 年重庆中考数学（B 卷）答案

一、选择题：1-4：ACBD 5-8：ADCB 9-12：CCDC 二、填空题：13、__12___ 14、_x≠2__ 15、__48___ 16、__8 ___ 17、 1 4 18、5 2 3 2 三、解答题： 19 题解：原式 9 2 1 3 2 9       20 题解：在R △ t ACD 中， CD=6 ， tanA= ∴ ∴ 在 △ sin = ∴ B =4 = AD BD AB AD  Rt BCD CD BC 中， 3 5 7 sin +cos = B 5 = ∴ B =8 BC= 8 +6 =10 2 2 cos = B ， BD BC  4 5 21 题解：原式  2 x x 4   1 (  1 x  2) x  2 2) x  2 2) ( x   2)(  ( x  2 x  2 x  解方程 1 x   2 1 3 x 2  5  得： 0 x  x  时，原式 2 当 1  3 2  x x   5 7 22 题解：（1） 22% ； 50 ；（2）由图可知：很不喜欢的共有 3 人，其中男性 2 人，女性 1 人. 由图可知，共有 6 种等可能情况，其中恰好都是男性（记为事件 A）有 2 种，其概率 1  . 3 解：（1）设 5 月份在市区销售了 x 千克，则园区里销售了（3000-x）千克. P  2 6 23 题由题意得： 6 x  4(3000  x ) 16000  解得 2000 x  ，则3000 x  1000

资料库

2014年重庆大渡口中考数学真题及答案B卷.doc

相关推荐

中考

热门标签

最新资料