logo资料库

龙格库塔方法解微分方程MATLAB程序.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.07M 资料格式：docx 举报 版权申诉
第1页 / 共6页
第2页 / 共6页
第3页 / 共6页
第4页 / 共6页
第5页 / 共6页
第6页 / 共6页
资料共6页，全文预览结束
    龙格-库塔方法是一种经典方法，具有很高的精度，它间接的利用了泰勒级数展开，避免了 高阶偏导数的计算。此处以最为经典的四级四阶龙格-库塔方法为例，计算格式如下              y n 1   K 1  K 2  K 3  K 4  n n f  h y 6  , f x y        f x   x x f  n n n n  1 , K  h 2 h 2 , h y  2 K 2  2 K 3  K 4  y n  K 1       h 2 h 2 hK K 2  3 , + y n  n 1 龙格-库塔法解一阶 ODE 对于形如 dy  dx   y a        , f x y y 0  a   x b 的一阶 ODE 初值问题，可以直接套用公式，如今可以 借助计算机方便的进行计算，下面给出一个实例 2 0 x y   x 1 dy dx   0 y        y  1 取步长 h=0.1，此处由数学知识可得该方程的精确解为 y  1 2  x 。在这里利用 MATLAB 编程，计算数值解并与精确解相比，代码如下： (1)写出微分方程，便于调用和修改 function val = odefun( x,y ) val = y-2*x/y; end (2)编写 runge-kutta 方法的函数代码
    function y = runge_kutta( h,x0,y0 ) k1 = odefun(x0,y0); k2 = odefun(x0+h/2,y0+h/2*k1); k3 = odefun(x0+h/2,y0+h/2*k2); k4 = odefun(x0+h,y0+h*k3); y = y0+h*(k1+2*k2+2*k3+k4)/6; end (3)编写主函数解微分方程,并观察数值解与精确解的差异 clear all h = 0.1; x0 = 0; y0 = 1; x = 0.1:h:1; y(1) = runge_kutta(h,x0,y0); for k=1:length(x) x(k) = x0+k*h; y(k+1) = runge_kutta(h,x(k),y(k)); end z = sqrt(1+2*x); plot(x,y,’*’);
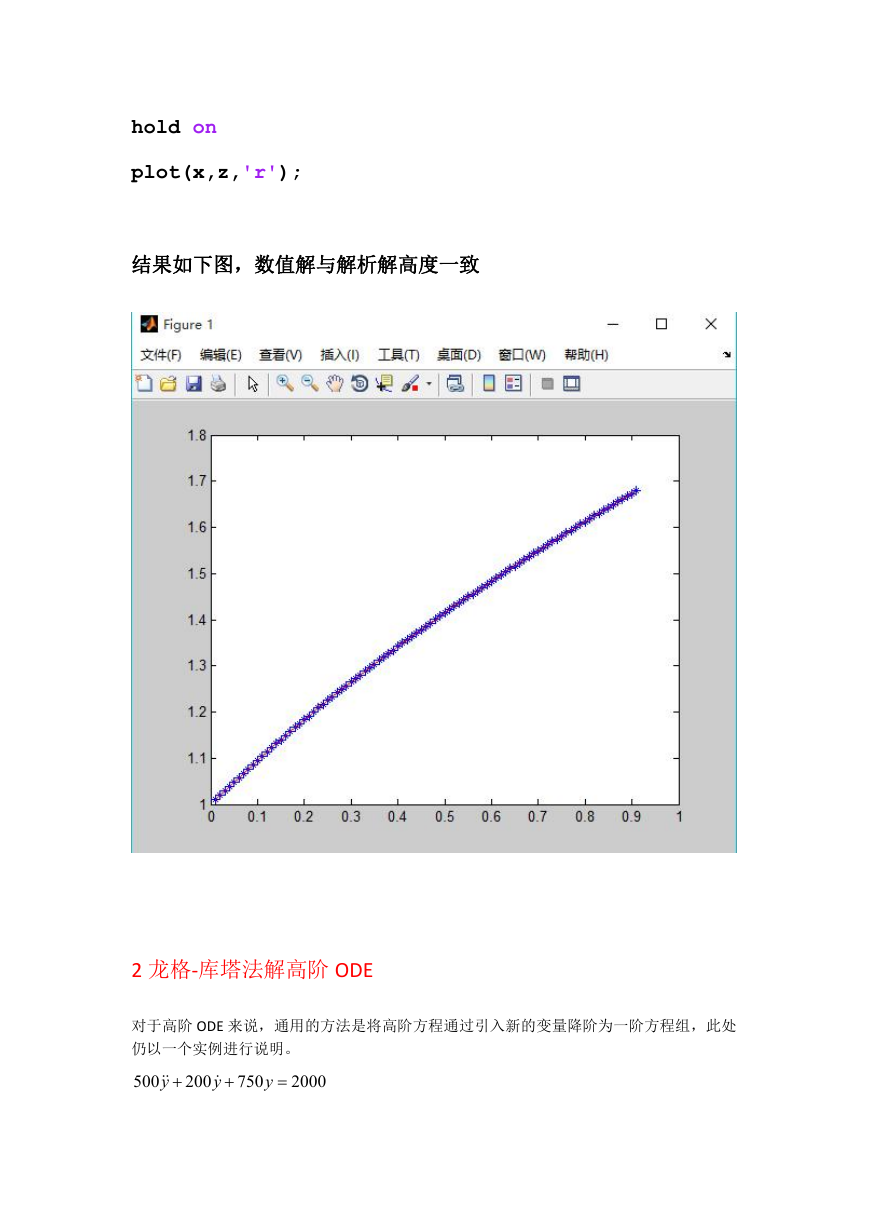
    hold on plot(x,z,'r'); 结果如下图，数值解与解析解高度一致 2 龙格-库塔法解高阶 ODE 对于高阶 ODE 来说，通用的方法是将高阶方程通过引入新的变量降阶为一阶方程组，此处 仍以一个实例进行说明。 500 y   200 y   750 y  2000
    这是一个二阶 ODE,描述的是一个物体的有阻尼振动情况。 y 初始条件为 0  00 y  0 ，将方程降阶，引入一个向量型变量 Y Y y      y   故有  Y  dY dt  y      y          y   2000 200 y  500   750 y       记 y Y    1 y Y    2 则  Y    2  Y     2000 200 2 Y   500    750 Y   1       至此，二阶方程降阶为一阶 方程组。值得注意的是此时再用龙格-库塔法进行求解时，代入的将是一个 Y 向量。同样利 用 MATLAB 进行计算，步长 h=0.05，时间周期为[0,20]. (1) 编写 ODE 函数 function Y = odefun1( ~,Y0 ) % 此处Y0为一个列向量，因为时间t未显含在一阶方程组中 % 所以ode函数的第一个参数为空，要根据具体情况而定。 Y = [Y0(2); (2000-200*Y0(2)-750*Y0(1))/500;]; end (2) 编写 runge-kutta 函数 function Y = rkfa( h,t0,Y0 ) k1 = odefun1(t0,Y0); k2 = odefun1(t0+h/2,Y0+h/2*k1); k3 = odefun1(t0+h/2,Y0+h/2*k2); k4 = odefun1(t0+h,Y0+h*k3); Y = Y0+h*(k1+2*k2+2*k3+k4)/6; end
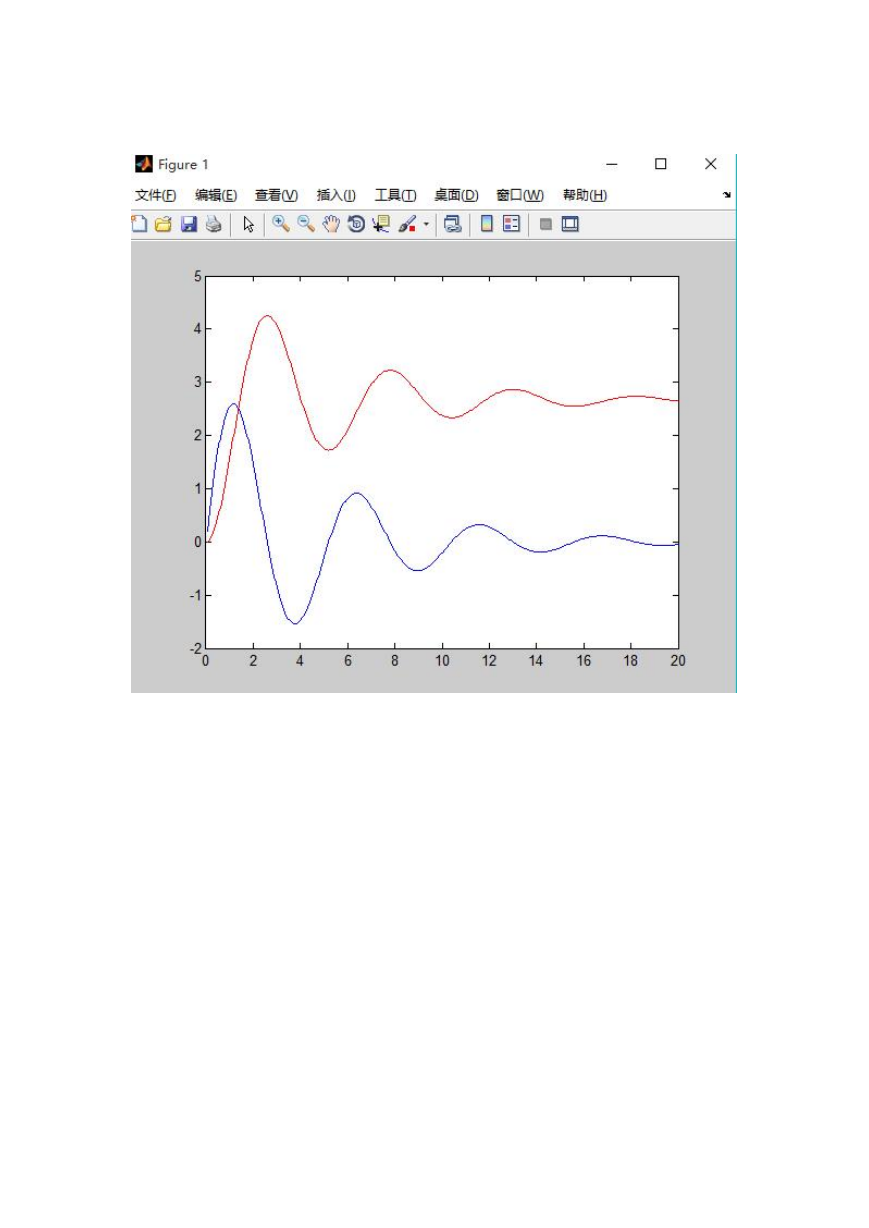
    (3) 编写主函数 clear all h = 0.05; t = 0.05:h:20; t0 = 0; Y0 = [0; 0];%初值 Y = cell(1,length(t)); Y{1} = rkfa( h,t0,Y0 ); z = zeros(2,length(t)); for k=1:length(t) Y{k+1} = rkfa( h,t0,Y{k}); z(1,k) = Y{k}(1); z(2,k) = Y{k}(2); end plot(t,z(1,:),'r');%位移y的图像 hold on plot(t,z(2,:));%速度y’的图像 求解结果如下图
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料