logo资料库

数学物理方程的MATLAB解法.docx

发布时间：2022-06-13 发布人：admin 分类：说明书 资料大小：0.51M 资料格式：docx 举报 版权申诉
第1页 / 共13页
第2页 / 共13页
第3页 / 共13页
第4页 / 共13页
第5页 / 共13页
第6页 / 共13页
第7页 / 共13页
第8页 / 共13页
资料共13页，剩余部分请下载后查看
    数学物理方程的 Matlab 解法 英才三班 范嘉义 2010013080020 黄一航 2010001030002 付良成 2010011010011 【摘要】本文主要介绍了用 Matlab 模拟弦振动的相关过程。并在初始速度为 零的条件下详细讨论了弦振动方程中系数 a 、以及初始位移的不为零的区间长 度对波形的影响。 【关键词】弦振动、Matlab、驻波解 【Abstract】This paper mainly discusses the process of string vibration based on Matlab. At the same time, in the condition of that the initial velocity is zero, some detailed discussing about the coefficient a in the equation and the influence of the length of the interval of nonzero displacement is included. 【Key Words 】 string vibration, Matlab, Standing wave solutions 一：引言 《数学物理方程》作为许多理工科学生的基础课程之一，对我们用数学方法 解决物理问题提供了基本的方法。尽管数学物理方程讨论的问题都有明确的表达 式，但是对于观察其物理意义却不是很直观。用 Matlab 软件模拟一些物理问题， 能够利于我们更加方便地观察和理解。本文主要讨论了用 Matlab 模拟弦振动方 程的一些问题。
    二：正文 1：用分离变量法求解弦振动方程的混合问题 在《数学物理方程》的第二章中，我们已经推导出了波动方程： u tt  2 a u xx 如果已知此波动方程初始条件和边界条件，则得到弦振动方程的混合问题： u u u      tt | | t x   0  0 2 ,0 a u xx 0, | u  x L  ( ), x u   , x L t   0  | t    0 t ( ) x  0 ( ( ), x   ( ) x 为已知函数） 于是我们从特解出发寻找满足初始条件的通解。假设方程具有分离变量形式 的特解 ( , ) u x t  ( ) T t X x ( ) ， 其中T 仅是关于 t 的函数，X 仅是关于 x的函数，代入泛定方程后得到 '' T 2 a T  '' X X ， 由于等式两边的变量是相互独立的，因此为使等式成立则令两边等于常数  . 得到两个常微分方程: '' X X  0 '' T 2 a T ，  0 其中为固有值。于是偏微分方程转化为了求解两个常微分方程。根据线 性空间的原理，只要能够找到足够多的线性无关的解，那么经过线性组合就能 找到满足初始条件的解。将初始条件代入分离变量形式的
    ( , ) u x t  ( ) T t X x ( ) 中得到: (0)  0 T t X L  ， ( ) ( ) 0 ( ) T t X 0   ( ) X L 即 (0) X 根据第一个常微分方程及初始条件及当满足某个特定条件时，可以解到 ( )X x 的非零解。对应的称为常微分边值问题的固有值或特征值，相应的非 零解 ( )X x 称为特征函数。根据分析，当满足方程 '' X   ) ( X L 0 时，方程存在非零解，其形式为 X (0)      X 0  0 时， 仅有当 ( ) X x  A cos  x B  sin x  代入边值条件得      A B 1 0 0, ( ) X L  A cos  L B  sin L   0 X (0) 解得 A  0, B sin L  ， 0 为使 ( )X x 不恒为零，应有 的特征函数 0B  解得的值为   n n 2 2  2 L 代入得到相应 ( ) X x n  B n 对于每一特征值方程 '' T sin n x  L 2 a T n 。  的解是 0
    n at  L 于是得到方程满足边界条件的可分离变量形式的特解为： n t  L ( ) T t n cos sin D n C   n ( , ) u x t n  ( ) T t X x n ( ) n  ( C n cos n t  L  D n sin n at  L ) B n sin n x  L 因为对每一个正整数 n 都有这种形式的解，所以这样的解有无穷多个。一 nu x t 均不能满足初始条件。为了使方程满足初始条件， nu x t 均是线性无关的，所以考虑将其无穷项叠加起来记 u x t 由于其每一项都满足泛定方程及初始条件，所以可以认为整体也满 般说来，任意一个 ( , ) 又观察得任意两个 ( , ) 为 ( , ) 足初始条件。将初始条件代入初始条件 ( ,0) u x   ( ) x    n 1  C sinn n x  L ， n x  L  n a  L D n sin   ， ( )x 的 fourier 级数，就能够定出 nC 与 得 1  n u x t ( ,0)   ( ) x 等式右边的级数恰好代表函数 ( )x nD 的值为       0 L  2 L 2 n a  C n   ( )sin D n  L   0 ( )sin n N  n  , d  L n  , d  L n N  级数每一项均满足泛定方程及边界条件，故级数解即满足泛定方程和边界条 件，又满足初始条件，因此它确实为方程的解。 2.用 Matlab 模拟弦振动方程以及分析 考虑以下混合问题
         x u tt | u | u t 2 5 ,   0  0 x ,0 u   xx | 0, u   1 x  | ( ), x u  t t t  0 1, 0  0 0  3 5 。 =  （x) 其中     sin 5 x    x 0, otherwise 显然，此混合问题可以有上述讨论的分离变量法的方法求解。并且可知 n 5 ， 即 其中 C n  2 1  0 ( , ) u x t    n 1  C n cos n t  sin  n x  ，  ( )sin , n   d n N  。 ①当 n=5 时， C 5 3 5   2 sin 2 5 2 xdx    1 cos 2 x dx  3 5 2 5  1 5 ②当 n 5 时， 3 5   2 sin x sin 2 5   C n n xdx    3 5  2 cos( 2 5 n  5) x   cos( n  5)   x dx = ( n 1 5)    sin      3 5  ( n  5)      sin    2 5 ( n  5)       
     ( n 1 5)      cos    3 5  ( +5) n      cos    2 5 ( +5) n        用程序②模拟弦振动方程，可得 从动画模拟中可以看到： ①波形是由初始位移平均分为两个运动方向相反的波构成的，在到达边界之 前可以看成是两个行波。 ②到达边界条件以后，发生反射（即沿初始运动方向的反方向传播）并产生 的相位移动（即产生了半波损失）。 ③从边界反射回来的两个波相向运动，相遇并产生叠加。然后按照原来的模 式继续传播。 用分离变量法解有限杆长的混合问题所得到的解叫做驻波解。怎么体现解的
    驻波性质呢？ 从式 ( , ) u x t    n 1  C n cos n t  sin  n x  可以发现，这个级数的每一项均为一个驻波。 现画出 n=20 时，即 20 cos 20 t  sin 20  C x  的各个时刻的波形： 从上图可以看到，它的振动图像是驻波的振动图像，它有以下特点： ①在某些坐标点，它的位移始终为零（即波节）；在某些坐标点，它的振幅为最 大（即波腹）； ②在一个相邻的波节（波腹）之间，各点的振幅不一样；
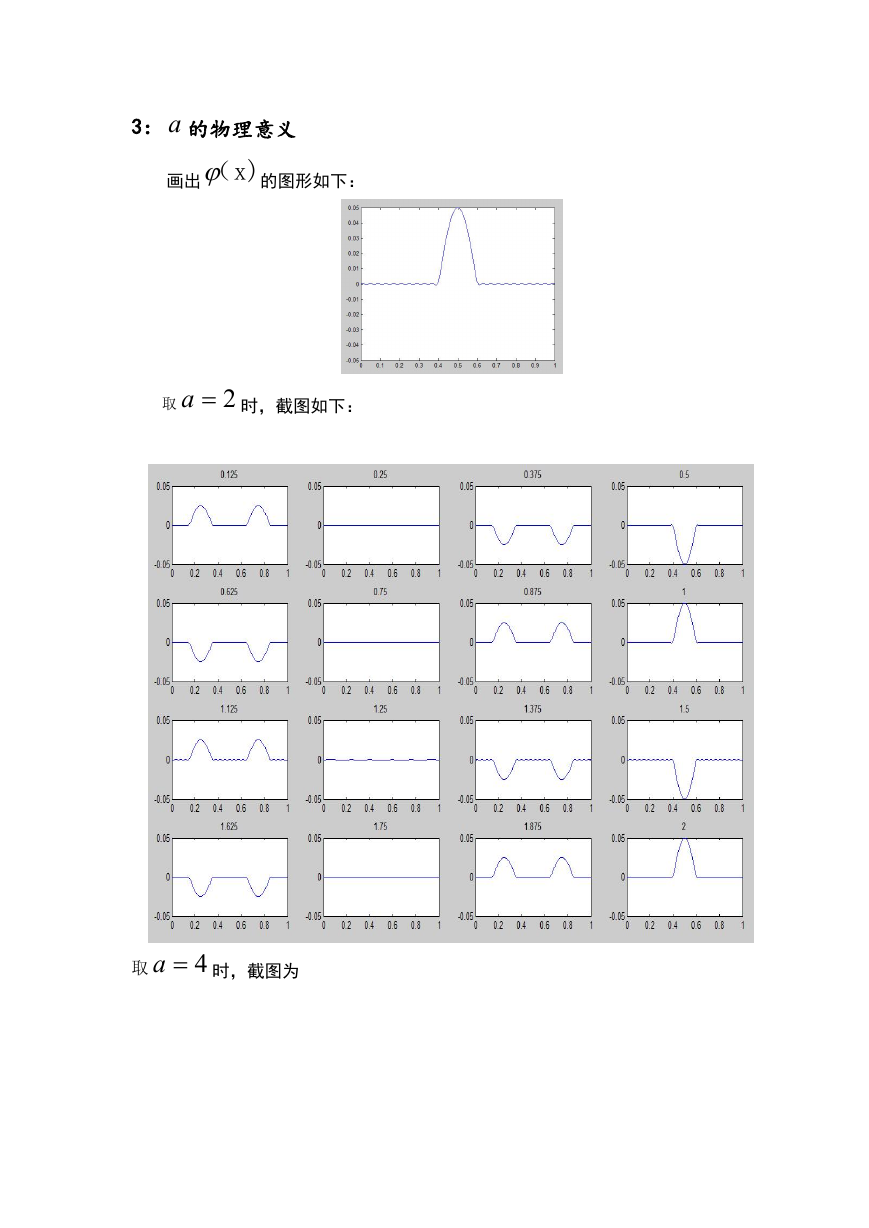
    3： a 的物理意义 画出（x)的图形如下： a  时，截图如下： 2 取 a  时，截图为 4 取
    分享到：
    赞 收藏

    相关推荐

    资料库

    课程资源

    共收录17145份资料，累计13个分类，关注成员有19位，主要包括：PHP,网络管理,网页制作,Java,.Net,数据库,3G/移动开发,C/C++,游戏开发,嵌入式,讲义,软件测试,专业指导

    热门标签

    PHP 网络管理 网页制作 Java .Net 数据库 3G/移动开发 C/C++ 游戏开发 嵌入式 讲义 软件测试 专业指导

    最新资料